13.7: Problemas y soluciones de la muestra

Ejercicio\(\PageIndex{1}\)

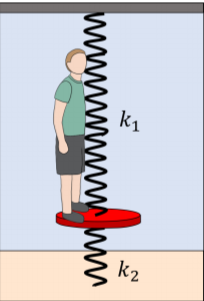
Ty (\(m=30\text{kg}\)) está probando una nueva pieza de equipo en su patio de recreo local. El equipo consiste en una plataforma que está conectada a dos muelles. El resorte superior (\(k_1=2400\text{N/m}\)) conecta la plataforma a la estructura del patio de recreo y el resorte inferior (\(k_2=3480\text{N/m}\)) (Figura\(\PageIndex{1}\)) la conecta al suelo. Cuando nadie está parado en la plataforma, la plataforma está\(50\text{cm}\) despegada del suelo. Cuando Ty está parado sobre la plataforma, oscila hacia arriba y hacia abajo, y el punto más bajo al que alcanza la plataforma es\(35\text{cm}\) fuera del suelo. Demuestre que se trata de un simple movimiento armónico y determine cuál será la velocidad máxima de Ty.

Figura\(\PageIndex{1}\): Equipo de patio de recreo hecho de plataforma conectada a dos muelles verticales.

Contestar

Primero, tenemos que resolver para la nueva posición de equilibrio de la plataforma,\(x_0\), cuando Ty está parado en la plataforma. Definimos el\(x\) eje para que el origen esté\(50\text{cm}\) por encima del suelo (la posición de equilibrio cuando nadie está parado sobre la plataforma) y elegimos la dirección positiva para estar hacia abajo (Figura\(\PageIndex{2}\)).

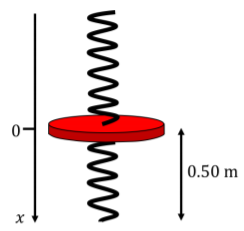
Figura\(\PageIndex{2}\): La plataforma cuando nadie está parado sobre ella.

A pesar de que desconocemos la masa de la plataforma, o las longitudes reales de reposo del muelle, no necesitamos conocerlas, ya que podemos modelar la plataforma sin nadie sobre ella como un solo resorte con constante de resorte\(k=k_1+k_2\) y posición de reposo\(x=0\).

Cuando Ty está parado sobre la plataforma, la suma de las fuerzas viene dada por su peso y la fuerza del “resorte efectivo”:\[\begin{aligned} \sum F=mg-(k_1+k_2)x\end{aligned}\] donde señalamos que, cuando la plataforma se mueve hacia abajo, tanto el resorte superior como el inferior ejercerán una fuerza hacia arriba (Figura\(\PageIndex{3}\)).

En equilibrio, la suma de las fuerzas es igual a cero. Podemos usar esto para resolver el desplazamiento en\(x_0\):\[\begin{aligned} 0&=mg-(k_1+k_2)x_0\\ \therefore x_0&=\frac{mg}{k_1+k_2}=\frac{(30\text{kg})(9.8\text{m/s}^{2})}{(2400\text{Nm})+(3480\text{Nm})}=0.05\text{m}\end{aligned}\] Confirmaremos que se trata de un simple oscilador armónico mostrando que el movimiento del sistema puede describirse mediante la ecuación:\[\begin{aligned} \frac{d^2x}{dt^2}&=-\omega^2x\end{aligned}\] Para alguna posición por\(x\) debajo del equilibrio, podemos reescribir Newton's segunda ley como:\[\begin{aligned} ma&=mg-(k_1+k_2)x\\ m\frac{d^2x}{dt^2}&=mg-(k_1+k_2)x\end{aligned}\] Para demostrar que se trata de un simple movimiento armónico, necesitamos combinar el lado derecho de la ecuación en un solo término. Encontramos antes eso\(mg=(k_1+k_2)x_0\), que podemos usar aquí: Ahora\[\begin{aligned} m\frac{d^2x}{dt^2}&=(k_1+k_2)x_0-(k_1+k_2)x\\ \frac{d^2x}{dt^2}&=\frac{(k_1+k_2)}{m}(x_0-x)\\ \frac{d^2x}{dt^2}&=-\frac{(k_1+k_2)}{m}(x-x_0)\\\end{aligned}\] definimos un\(x'\) eje tal que\(x'=x-x_0\). Esto significa que el origen del\(x'\) eje está en la nueva posición de equilibrio:

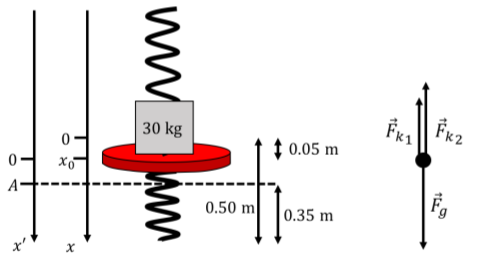
Figura\(\PageIndex{3}\): Las fuerzas que actúan sobre la plataforma y nuestro nuevo sistema de coordenadas.

Ahora podemos reescribir nuestra expresión usando el\(x'\) eje:\[\begin{aligned} \frac{d^2x}{dt^2}&=-\frac{(k_1+k_2)}{m}x'\end{aligned}\] Esta ecuación nos dice que se trata de un simple movimiento armónico sobre la nueva posición de equilibrio, donde\(\omega=\sqrt{(k_1+k_2)/m}\). Sabemos que el punto más bajo al que alcanza la plataforma es de 35 cm sobre el suelo, lo que, en nuestro\(x'\) eje, corresponde a\(x'=10\text{cm}\) (Figura\(\PageIndex{3}\)). Así, la amplitud de la oscilación es\(A=0.1\text{m}\). Debido a que se trata de un simple movimiento armónico, sabemos que la posición de la plataforma se puede describir mediante la siguiente función:\[\begin{aligned} x'(t)&= A \cos(\omega t + \phi)\end{aligned}\] Nos fijamos\(t=0\) para ser cuando la plataforma está en su punto más bajo (\(x'=A\)). El valor de\(\phi\) es así:\[\begin{aligned} x'(0)&= A \cos(\omega (0) + \phi)\\ A&= A \cos(\phi)\\ 1&=\cos(\phi)\\ \therefore \phi&=0\end{aligned}\] La velocidad viene dada por:\[\begin{aligned} v(t)=\frac{d}{dt}x(t) &= -A\omega\sin(\omega t + \phi)\\ &=-A\omega\sin(\omega t)\end{aligned}\] La velocidad se maximizará cuando\(\sin(\omega t)=1\quad \textrm{or} -1\). Entonces, la velocidad máxima será:\[\begin{aligned} |v|&=A\omega\\ |v|&=A\sqrt{\frac{(k_1+k_2)}{m}}\\ |v|&=(0.1\text{m})\sqrt{\frac{(2400\text{Nm}+3480\text{Nm})}{30\text{kg}}}\\ |v|&=1.4\text{m/s}\end{aligned}\]

Ejercicio\(\PageIndex{2}\)

Un péndulo torsional consiste en una varilla horizontal suspendida de un alambre vertical. Cuando se gira la varilla para que se desplace un ángulo\(\theta\) del equilibrio, el alambre (que ahora está torcido) proporciona un par de restauración alrededor del eje del alambre dado por:\[\begin{aligned} \tau=-\kappa\theta\end{aligned}\] donde\(\kappa\) está el coeficiente de torsión, que depende de la rigidez del alambre. Podrán notar que esta fórmula se parece mucho a la ley de Hooke.

a. se construye un péndulo torsional uniendo dos pequeñas masas esféricas (se puede suponer que son masas puntuales, cada una de masa\(m\)) a los extremos de una varilla delgada (sin masa) de longitud\(L\) y uniendo un alambre al centro de la varilla (Figura\(\PageIndex{4}\)). Cuando desplazas una de las masas por un ángulo\(\theta\) y la sueltas, encuentras que oscila con un periodo\(T\). Encontrar una expresión para el coeficiente de torsión\(\kappa\),, en términos de\(T\)\(m\), y\(L\).

Figura\(\PageIndex{4}\): Un péndulo torsional. El lado derecho muestra una vista superior.

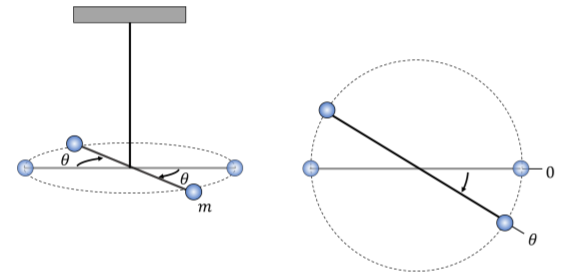
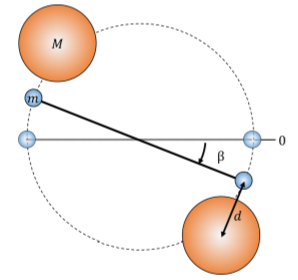
b. colocas dos esferas muy grandes, cada una de masa\(M\), cerca de cada una de las esferas pequeñas (como se muestra en la Figura\(\PageIndex{5}\)). Cada una de las esferas pequeñas será actuada por una fuerza de gravedad procedente de la esfera grande más cercana. El péndulo está en equilibrio cuando se desvía un ángulo\(\beta\) de su posición de equilibrio original. En el nuevo equilibrio, los vectores de desplazamiento que conectan los centros de esferas grandes y pequeñas tienen una magnitud\(d\) y son esencialmente perpendiculares a la varilla. Encontrar una expresión para la constante gravitacional universal\(G\), en términos de las masas, la longitud de la varilla y el período medido en la parte a).

¡Dato curioso! Esta configuración se asemeja a un experimento realizado por Henry Cavendish que se utilizó por primera vez para determinar el valor\(G\) y probar la Teoría Universal de la Gravedad de Newton.

Figura\(\PageIndex{5}\): Dos esferas muy grandes se colocan cerca de cada una de las pequeñas masas en el péndulo torsional (vista superior). En el nuevo equilibrio, cada masa pequeña está a una distancia d de la masa grande más cercana.

Contestar

La única fuerza que crea un par en las masas es la fuerza restauradora de la torsión del alambre. La versión dinámica rotacional de la Segunda Ley de Newton relaciona este par con la aceleración angular,\(\alpha\) de la varilla:\[\begin{aligned} I\alpha=-\kappa\theta\end{aligned}\] donde\(I\) está el momento de inercia de la varilla. Reescribiendo\(\alpha\) más explícitamente como la segunda derivada de tiempo del ángulo, obtenemos:\[\begin{aligned} I\frac{d^2\theta}{dt^2}&=-\kappa\theta\\ \frac{d^2\theta}{dt^2}&=-\frac{\kappa}{I}\theta\\\end{aligned}\] Por inspección, podemos ver que el péndulo torsional es un simple oscilador armónico, donde\(\omega=\sqrt{\kappa/I}\). El periodo del movimiento es por lo tanto:\[\begin{aligned} T&=\frac{2\pi}{\omega}\\ T&=2\pi\sqrt{\frac{I}{\kappa}}\end{aligned}\] Podemos reorganizar esta expresión para obtener\(\kappa\):\[\begin{aligned} T^2&=\frac{4\pi^2I}{\kappa}\\ \kappa&=\frac{4\pi^2I}{T^2}\end{aligned}\] El momento de inercia para una de las masas es\(m(L/2)^2\), donde\(L/2\) está la distancia de la masa al eje de rotación. El momento de inercia para las dos masas adheridas a la varilla sin masa es:\[\begin{aligned} I&=2m\left(\frac{L}{2}\right)^2=\frac{mL^2}{2}\\\end{aligned}\] Poner esto en nuestra expresión para\(\kappa\):\[\begin{aligned} \kappa=\frac{2\pi^2mL^2}{T^2}\end{aligned}\]

Las dos fuerzas que proporcionan pares para las pequeñas esferas son la gravedad y la fuerza ejercida por el alambre de torsión. Cada una de las esferas pequeñas experimentará una fuerza debida a la gravedad de la esfera grande más cercana. En equilibrio, la fuerza debida a la gravedad sobre una de las esferas pequeñas es por lo tanto:\[\begin{aligned} F_g=\frac{GMm}{d^2}\end{aligned}\] Suponiendo que, en equilibrio, el vector de fuerza es perpendicular a la varilla, el par de una de las esferas grandes es solo la fuerza multiplicada por la distancia al eje de rotación. Dado que hay dos esferas grandes, cada una de las cuales crea un par en el péndulo, el par total debido a la gravedad es:\[\begin{aligned} \tau_g&=2F_g\frac{L}{2}\\ &=F_gL\\ &=\frac{GMm}{d^2}L\end{aligned}\] (Tenga en cuenta que\(\tau g\) es el par debido a la gravedad solo en equilibrio). Podemos usar la segunda ley de Newton para que el péndulo encuentre una expresión para\(G\). En equilibrio, el par neto es igual a cero, y el ángulo de deflexión es\(\beta\):\[\begin{aligned} \tau_{net}&=\tau_{wire}-\tau_g\\ 0&=\tau_{wire}-\tau_g\\ \tau_g&=\tau_{wire}\\ \frac{GMm}{d^2}L&=\kappa\beta\\ \therefore G&=\frac{\kappa\beta d^2}{LMm}\end{aligned}\] Usando nuestra expresión para\(\kappa\) encontrado en la parte a), esto se convierte en:\[\begin{aligned} G=\frac{2\pi^2L\beta d^2}{MT^2}\end{aligned}\]