12: Una paradoja cuántica y los experimentos

Objetivos

La mecánica cuántica hace predicciones probabilísticas sobre los posibles resultados de un experimento con objetos microscópicos, partículas. Esta es una declaración estadística concerniente a muchas partículas. Se puede suponer que existe una ley no estadística más profunda, es decir, determinista para partículas individuales que predice lo que debería suceder con esa partícula específica.

¿Hay alguna teoría o ley más profunda que determine con certeza el resultado experimental? Debe existir tal teoría según Einstein, lo que implica que la mecánica cuántica no puede ser una teoría completa. Por otro lado, según Bohr —quien fue otro fundador de la teoría cuántica— no hay lugar para una teoría más profunda, no podemos predecir nada más sobre una sola partícula, sino probabilidades.

Prerrequisitos

Capítulo 1. Polarización de ondas de luz plana en óptica clásica.

La paradoja de la EPR, la versión de Bohm

En esta última sección consideramos ciertas cuestiones principales de la mecánica cuántica que están conectadas con la esencia misma del sujeto, es decir, con la naturaleza de las probabilidades que aparecen en la teoría. En la física clásica una medición hace un registro del valor de una cantidad física de una partícula, un cuerpo o un sistema que se supone que es una propiedad de la partícula que existía antes de la medición, e independientemente de si la medimos o no. En contraste con esto, en la física cuántica —se puede preparar un conjunto de partículas para tener exactamente la misma propiedad desde cierto punto de vista, aún así pueden mostrar resultados de medición bastante diferentes, desde el punto de vista de otra propiedad.

El ejemplo más simple está conectado con la polarización de la luz, o dicho en lenguaje cuántico: polarización de fotones. Según la mecánica cuántica si se polariza una onda transversal plana, y su plano de polarización forma un ángulo\(θ\) con otra dirección de polarización, entonces los fotones en el haz se polarizan también en esa última dirección con una amplitud de probabilidad\(cos⁡θ\). Esto significa, por ejemplo, que si la polarización hace un ángulo\(θ\) con la dirección horizontal y por lo tanto un ángulo\(π/2−θ\) con la dirección vertical, entonces las amplitudes de probabilidad correspondientes son\(cos⁡θ\) y\(cos⁡(π/2−θ)=sin⁡θ\), respectivamente. De acuerdo con el papel fundamental de la física cuántica las probabilidades son a su vez los cuadrados (valor absoluto) de las amplitudes. Entonces la probabilidad de encontrar un solo fotón del haz original que se va a polarizar horizontalmente es\(cos^{2}⁡θ\) mientras que la probabilidad de ser polarizado verticalmente es\(sin^{2}⁡θ\). Esta ley se verifica fácilmente ya con un clásico campo de onda plana de intensidad el\(I_{0}\) cual está polarizado para que forme un ángulo\(θ\) con la dirección horizontal. El haz se dirige a un cristal de calcita que lo separa en dos haces de manera que uno de ellos se polariza horizontalmente y el otro verticalmente —estas son las direcciones propias de la calcita— y los dos haces son distintos, de manera que se pueden verificar individualmente. Entonces la intensidad del haz polarizado horizontalmente después de la calcita será\(I_{0}cos^{2}⁡θ\), mientras que la del haz polarizado verticalmente lo será\(I_{0}sin^{2}⁡θ\). Como la intensidad es proporcional al número de fotones, esto es una prueba de la ley de probabilidad. La técnica actual también permite verificar las probabilidades por sí mismas, ya que los fotones también pueden ser detectados uno a uno por detectores sensibles.

Será importante que podamos fijar la calcita para que sus direcciones propias no sean horizontales y verticales, a lo que posteriormente llamaremos ajuste A, sino también en cierto modo, digamos B o C, de manera que las dos direcciones propias sean distintas a las de la configuración A. Notemos, sin embargo, que las dos direcciones propias son siempre ortogonales entre sí.

Surge la siguiente pregunta: qué determina la dirección de polarización final del fotón. Según la mecánica cuántica el fotón se vuelve vertical, u horizontal durante la interación con el aparato de medición. Esto no está codificado en la partícula entrante, por lo tanto es principalmente imposible responder a la pregunta con certeza, la mayoría podemos decir son las probabilidades de los dos posibles resultados diferentes. Dicho de otra manera, la medición no establece una propiedad previamente existente del fotón, más bien es la propia medida la que crea la propiedad con la probabilidad apropiada.

Esta respuesta, sin embargo, no satisface a todos, porque uno puede imaginar una respuesta diferente, también, es decir, asumiendo que para cada fotón ambas propiedades existían antes de la medición, es decir, estaba polarizado en digamos\(45^{\circ}\) y al mismo tiempo tenía la propiedad de ser horizontal polarizadas, si obtuvimos este último resultado durante la medición. Otra cuestión es que la mecánica cuántica no da cuenta de ambas propiedades simultáneamente, ya que no puede dar con probabilidad unitaria —es decir, con certeza completa— la dirección de polarización de un solo fotón para dos direcciones no paralelas o no ortogonales. Esto significaría entonces que existe una especie de teoría, más profunda que la mecánica cuántica, según la cual estas propiedades están presentes simultáneamente y exactamente en el objeto medido. Desde el punto de vista de la teoría cuántica el parámetro que daría el resultado con certeza no está presente, por lo que es un parámetro oculto como se le llama en estas teorías.

Como la mecánica cuántica no da cuenta de estos parámetros, no puede ser una descripción completa de la realidad física. Este fue el punto de vista de A. Einstein, y esto quedó expuesto de la manera más desconcertante en el famoso artículo de A. Einstein, B. Podolsky y N. Rosen en 1935: “¿Puede considerarse completa la descripción cuánto-mecánica de la realidad física?” Al final del trabajo llegaron a la conclusión de que la mecánica cuántica no es completa, pero agregan que tal teoría aparecerá en el futuro.

Al principio los autores del artículo EPR tratan de dar una definición exacta de lo que consideran una teoría completa:

“Una teoría es completa si cada elemento de la realidad física tiene su contraparte en la teoría física”.

Pero, ¿qué es un elemento de la realidad física? Dan la siguiente respuesta:

“Si, sin molestar de ninguna manera a un sistema, podemos predecir con certeza (es decir, con probabilidad igual a la unidad) el valor de una cantidad física, entonces existe un elemento de realidad física correspondiente a lo esta cantidad física”.

Einstein, Podolsky y Rosen (EPR) presentan la descripción y el análisis de un experimento imaginado, (el llamado Gedankenexperiment) realizado sobre un par de partículas cuánticas, que según los autores muestra que la mecánica cuántica no es una teoría completa en el sentido que la requieren. En su ejemplo consideran la medición de las posiciones y los momentos de un par de partículas, que emergen en un proceso de desintegración. En lugar de eso es más sencillo considerar otra variante del experimento, cuando se hace con un par de sistemas de dos estados, ya que solo hay dos resultados posibles en un solo aparato de medición, en lugar de los infinitamente muchos resultados posibles al medir la posición o/y momento. Tal variante de la paradoja del EPR fue propuesta por David Bohm en 1957 con pares de partículas de espín 1/2, o lo que analizaremos, con fotones que tienen dos autoestados de polarización ortogonal.

Lectura adicional

Puede descargar el documento original del EPR bajo este enlace:
http://prola.aps.org/pdf/PR/v47/i10/p777_1

Las características esenciales del experimento, realizado muchas veces desde la propuesta de Bohm, son las siguientes. Una fuente especial genera pares de fotones, de tal manera que los miembros del par se propagan en diferentes direcciones espaciales, digamos, uno a la izquierda, el otro a la derecha. Las propiedades de polarización de los miembros se miden de forma independiente. Uno coloca dos dispositivos de medición de polarización perpendicularmente a la propagación de los haces. Estos son, por ejemplo, cristales de calcita en los caminos de los dos fotones que los atraviesan, y miden las propiedades de polarización de los fotones. Los dispositivos se pueden configurar haciendo diferentes ángulos con la dirección horizontal. Los ajustes posibles de los dispositivos serán denotados por distintas letras mayúsculas\(A,B,C\) y los dos autoestados correspondientes de los dispositivos por\(A+\) y\(A−\);\(B\) + y\(B−\); y\(C+\) y\(C−\) respectivamente. Con una fuente de fotones apropiada se puede lograr que exista una estricta anticorrelación en la medición entre los miembros de un par, lo que significa lo siguiente. Supongamos que los dispositivos están configurados de manera idéntica, en ambos lados de la fuente. Entonces ambos fotones pasan por el mismo tipo de dispositivo, digamos horizontal-vertical, para ser denotados por A. Se observa entonces que si uno de los fotones se polariza horizontalmente\(A−\) a la izquierda, su par siempre resulta estar polarizado verticalmente\(A+\), a la derecha, o viceversa. Lo mismo sucede si ambos polarizadores se fijan en cualquier dirección digamos B que es diferente de A, pero idéntico para ambos fotones. Si\(B+\) denota\(60^{\circ}\) de la horizontal y\(B−\) medias\(−30^{\circ}\) de la horizontal, entonces si uno de los fotones viene está polarizado adentro\(B+\), su par será\(B−\), o al revés. Así, los estados de polarización de un miembro dado son siempre ortogonales entre sí. Tales pares de partículas se denominan pares EPR. Esta anticorrelación del par se desprende de la forma en que uno los crea, que se detallará a continuación.

Un estado EPR de un par de fotones es:

\(\psi=\frac{1}{\sqrt{2}}\left\{(A+)_{1}(A-)_{2}-(A-)_{1}(A+)_{2}\right\}\)(12.1)

donde el subíndice marca la partícula: 1 va a la izquierda y 2 a la derecha. El primer término en el estado anterior dice que el fotón 1 está polarizado verticalmente, mientras que el fotón 2 se polariza horizontalmente. El segundo término significa todo esto al revés. Lo que es importante, la mecánica cuántica permite la superposición de las dos posibilidades. Ya hemos encontrado un estado similar cuando consideramos el estado singlete de espín de los dos electrones en la\(H_{2}\) molécula en el Capítulo 7.

Problema 12.1

Mostrar que el estado (12.1) anterior no puede escribirse como producto de dos estados de una partícula.

Figura 12.1: Dos posibles estados propios del polarizador A se denotan por\(A+\) y\(A−\). Se utiliza la misma notación en el caso del polarizador BB, los dos estados propios son\(B+\) y\(B−\). Existe una estricta anticorrelación entre los resultados en los dos lados, si los dispositivos se configuran de manera idéntica

Pero entonces es suficiente medir sólo en un fotón del par. Podemos pensar que conocemos el resultado para el otro miembro, incluso sin hacer la medición, porque siempre será opuesto al de su pareja. Por lo tanto, sin molestarlo, podemos predecir su valor, así es el elemento de la realidad según EPR. Hay que añadir aquí, que es imposible que medimos un valor a\(A+\) la izquierda porque medimos a\(A−\) la derecha. La propagación de esta información necesita tiempo, pero los dos eventos pueden tener una separación espacial (en el sentido de la teoría de la relatividad), lo que significa que solo una señal más rápida que la luz podría influir en el resultado de la medición en el otro lado, dependiendo del resultado de uno de los lados. Este es el principio de localidad tanto enfatizado por la teoría de la relatividad de Einstein. Para concluir: la propiedad de polarización del fotón no medido es el elemento de la realidad, y una teoría completa debe asignarle un valor bien definido en el sentido definido por EPR.

Pero hay incluso más que eso: en el caso del par EPR podemos decir el estado de una partícula exactamente incluso desde el punto de vista de dos dispositivos incompatibles, lo que es imposible en la mecánica cuántica, en principio. Pongamos dos dispositivos diferentes en los dos lados.

Figura 12.2:

Si medimos en el lado izquierdo la propiedad A (cantidad física), entonces también conocemos el estado de su par a la derecha desde el punto de vista de A, debido a la perfecta anticorrelación. Será perpendicular a la dirección medida a la izquierda. Pero al mismo tiempo a la derecha podemos medir con otro tipo de aparato, que mida el inmueble B. De esta manera podemos exponer ambas propiedades de la partícula dada, una de ellas se desprende del valor medido en su mate a la izquierda, la otra se mide realmente. Lo mismo es cierto para su pareja. Esto significaría que ambas propiedades están bien definidas en el caso de una sola partícula, mientras que según QM esto es imposible, si A y B tienen diferentes direcciones propias como se ve en la figura 12.2. En mecánica cuántica solo se da la amplitud de probabilidad y una probabilidad correspondiente si A y B hacen un ángulo diferente de\(0^{\circ}\) o\(90^{\circ}\). Este razonamiento llevó a EPR a la conclusión de que la QM, que no da cuenta de dos elementos incompatibles de la realidad física, no puede ser completa. En contraste con la afirmación de EPR, N. Bohr argumentó que las dos partículas forman parte de un único sistema cuántico inseparable, según la redacción actual se encuentran en un estado enredado, por lo tanto una medición en una de sus partes influye inmediatamente en su otra parte, aunque estén muy lejos el uno del otro dejó que las dos medidas dos eventos espaciales en el sentido de la relatividad especial. Pero esta afirmación contradice uno de los principios más fundamentales de la física, la localidad. Por lo tanto, Einstein no pudo aceptar los argumentos de Bohr y el debate y la paradoja permanecieron sin resolver durante unos 30 años.

Desigualdades de campana con fotones

Para decidir la cuestión, John Bell propuso un arreglo experimental explícito en 1964. Uno tiene que medir no dos sino tres cantidades diferentes (polarizaciones ortogonales) A, B y C para los pares de fotones, de manera que los tres ajustes posibles de los polarizadores se eligen aleatoriamente e independientemente entre sí. Resulta, que con base en el número de pares medido experimentalmente se puede decidir si la mecánica cuántica, o la hipótesis de Einstein es correcta, diciendo esta última que las partículas deben tener polarizaciones bien definidas en diferentes direcciones simultáneamente. Aquí se presentará la idea original de Bell tal y como fue discutida por Eugene Wigner.

Figura 12.3:

Supongamos que los miembros del par tenían una polarización bien definida antes de la medición:\(+\) o\(−\) en cada una de las tres direcciones A, B y C. Como muestran las mediciones, en un solo par la polarización de las dos partículas siempre son ortogonales entre sí, se muestran explícitamente si usamos los mismos ajustes en ambos lados. Los 8 tipos posibles de los pares se muestran en la tabla 12.1, y denotemos el número medido de un tipo dado de pares por\(N_{k}\).

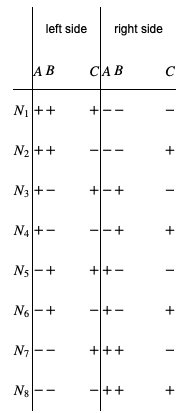
Cuadro 12.1:

Consideremos ahora los pares para los que resultó la partícula que iba a la izquierda\(A+\), mientras que el que iba a la derecha salió como\(C+\). Estos eventos, por supuesto, solo estarán presentes si el dispositivo de la izquierda se configuró en A mientras que el de la derecha estaba configurado en C. El número de tales pares se denotará aquí por\(N(A+,C+)\), y de acuerdo con la tabla anterior\(N(A+,C+)=N_{2}+N_{4}\). De igual manera el número de pares para los que obtuvimos A+A+ a la izquierda y B+B+ a la derecha el resultado es\(N(A+,B+)=N_{3}+N_{4}\). Finalmente el número de los que teníamos a\(B+\) la izquierda y a\(C+\) la derecha estaba\(N(B+,C+)=N_{2}+N_{6}\).

Según la simple desigualdad

\(N_{2}+N_{4} \leq\left(N_{3}+N_{4}\right)+\left(N_{2}+N_{6}\right)\)(12.2)

válido porque por definición todos los números\(N_{i}\) son enteros no negativos, obtenemos:

\(N(A+, C+) \leq N(A+, B+)+N(B+, C+)\)(12.3)

Es importante que se\(N(A+,C+),N(A+,B+),N(B+,C+)\) pueda medir el número de pares, y el resultado experimental se pueda comparar con la desigualdad obtenida anteriormente. Antes de continuar, sin embargo, reformulamos la desigualdad (12.3) en probabilidades, para compararla con la mecánica cuántica, que dan sus resultados en términos de probabilidades.

Deje que\(P(A+,C+)\) la probabilidad, que al elegir aleatoriamente las direcciones nos fijamos a la izquierda el dispositivo a A, y midió un resultado\(A+\), mientras que la medición en la partícula derecha pasó de nuevo por elección aleatoria en la dirección C, y resultó en\(C+\). Entonces

\(P(A+, C+)=\frac{N(A+, C+)}{\sum_{i=1}^{8} N_{i}}\)(12.4)

y de manera similar\(P(A+, B+)=\frac{N(A+, B+)}{\sum_{i=1}^{8} N_{i}}, P(B+, C+)=\frac{N(B+, C+)}{\sum_{i=1}^{B} N_{i}}\), si hicimos suficientes mediciones. En consecuencia, la desigualdad (12.3) puede escribirse como

\(P(A+, C+) \leq P(A+, B+)+P(B+, C+)\)(12.5)

Se trata de una desigualdad de Bell, que —como debemos recordar— se derivó utilizando el supuesto de que los pares tenían propiedades bien definidas antes de que se realizara la medición. No hubo argumentos mecánicos cuánticos para obtenerlo.

Entonces veamos lo que dice QM sobre las probabilidades que ocurren en (12.5) como se muestra en la siguiente figura. En una medida real uno tiene cristales idénticos en ambos lados, y se rotan aleatoriamente e independientemente entre sí en tres direcciones A, B y C. Si en el lado izquierdo medimos\(A+\) por ejemplo, entonces su par debería estar en estado\(A−\). Pero medimos digamos C en él, y el resultado medido en el socio puede ser cualquiera\(C+\) o\(C−\). La amplitud de probabilidad de obtener el resultado de que esta otra partícula se polariza en la dirección\(ê_{θ}\) es\(cos⁡θ\), donde\(θ\) está el ángulo con\(A−\). La probabilidad correspondiente es así\(cos^{2}⁡θ\). O queremos expresarlo con el ángulo hecho con\(A+\), que es\(α=π/2−θ\), entonces la probabilidad es\(sin^{2}⁡α\). Al elegir aleatoriamente las tres direcciones posibles en ambos lados con probabilidades iguales\(1/3\), la probabilidad de todos los ajustes posibles del par de los aparatos es igual a\(1/9\). La probabilidad de obtener digamos A+A+ a la izquierda antes de medir a la derecha es\(1/2\), entonces con un ajuste dado de ambos cristales la probabilidad es e.g.\(P(A+, C+)=\frac{1}{18} \sin ^{2}(A+, C+)\), donde\((A+,C+)\) denota aquí el ángulo entre las direcciones\(A+\) y\(C+\).

Figura 12.4: Violación de la desigualdad de Bell

Escojamos específicamente las direcciones que se muestran en la figura, es decir, dejar que las direcciones propias de A, B y C se roten consecutivamente por\(30^{\circ}\). En otras palabras elegimos\((A+,B+)=(B+,C+)=30^{\circ}\) y\((A+,C+)=60^{\circ}\). Entonces las probabilidades mecánicas cuánticas dan el siguiente resultado:

\(P(A+, C+)=\frac{1}{18} \sin ^{2} 60^{\circ}, \quad P(A+, B+)=\frac{1}{18} \sin ^{2} 30^{\circ}, \quad P(B+, C+)=\frac{1}{18} \sin ^{2} 30^{\circ}\)(12.6)

Si sustituimos estas probabilidades en (12.5) observamos que estos resultados no la obedecen, porque eso requeriría el cumplimiento de\(\sin ^{2} 60^{\circ} \leq 2 \sin ^{2} 30^{\circ}\), es decir, la desigualdad

\(\frac{3}{4} \leq \frac{1}{2}\)(12.7)

lo que obviamente es falso.

Esto significa que al elegir las direcciones apropiadas para los cristales las probabilidades mecánicas cuánticas correspondientes violan la desigualdad de Bell. Esto resulta ser entonces una posibilidad experimental para decidir si la mecánica cuántica o las desigualdades de Bell son válidas en el mundo físico real. De acuerdo con los experimentos que miden directamente los números\(N(A+,C+)\) etc. resultó que las desigualdades de Bell no son válidas para las direcciones A, B y C apropiadamente elegidas como arriba pero los resultados están de acuerdo con las predicciones de QM.

Todo esto debería significar que en la derivación de la Campana las desigualdades deben ser algo que contradiga lo que hay en el mundo físico real. Hay dos posibilidades de errores. Una de ellas podría haber sido que rellenando la tabla 12.1 asumimos que una partícula, y su pareja poseía dos, (en realidad tres) propiedades de polarización diferentes ya antes de la medición, sí existían en ellas independientemente de la medición que se realizara sobre ellas posteriormente. El otro posible error podría ser que existe una comunicación no local entre los dos miembros de un par, es decir, el estado medido de una de las partículas depende de la medición en su pareja distante. (Sin embargo se puede demostrar, que la información no puede transmitirse de esta manera con una velocidad más rápida que la luz, porque la transferencia de información requeriría un canal de comunicación clásico adicional, y la velocidad de la transferencia está determinada por la velocidad de la señal clásica. Eso quiere decir que la localidad no es violada en este sentido). Ambas posibilidades, como razones de la discrepancia, contradicen con los conceptos tradicionales sobre el mundo natural. En el primer caso contradice el supuesto de que todas las propiedades posibles de una partícula, incluyendo las propiedades incompatibles, tienen un valor bien definido antes e independientemente de la medición. Esta suposición suele llamarse como realismo. La segunda posibilidad contradice la localidad, en el sentido de que el resultado de la medición influye instantáneamente en otra medición distante, espacialmente separada.

Experimentos y desigualdades de Bell

Los primeros experimentos sobre la validez o violación de las desigualdades de Bell fueron realizados por J. F. Clauser y compañeros de trabajo en 1972. Un experimento posterior de A. Aspect (1982) fue el primero, donde se realizaron los ajustes de los dos cristales para que la separación de estos dos eventos fuera espacial, es decir, una señal de luz imaginada que partiría de uno de los cristales al momento de su medición no pudiera llegar al otro antes de él midió el estado de la otra partícula.

Aquí mostramos la configuración del experimento de A. Zeilinger (1995) donde el par de fotones emergió de un cristal no lineal.

Figura 12.5: Generación de un par de fotones enredados. (En la figura los colores son ficticios, el color verde corresponde a los fotones infrarrojos de longitud de onda 702 nm.)

Cuando los fotones de un láser UV de longitud de onda 351 nm pasan a través del cristal no lineal, una pequeña parte de ellos se dividen en dos fotones con menor energía y por lo tanto con menor frecuencia. Este proceso se denomina conversión descendente paramétrica en óptica no lineal. Los dos haces emergentes dejan el cristal a lo largo de la superficie de dos conos, satisfaciendo la conservación de energía y momento. Entre los pares algunos compartirán por igual la energía y el impulso originales, su longitud de onda será idénticamente 702 nm (esto se llama el caso degenerado). Con un ajuste apropiado del cristal se puede lograr que la polarización de los miembros sean siempre ortogonales entre sí, como se supone para el par EPR en la discusión anterior. En este último caso el ángulo en los ápices de los dos conos es idéntico y a lo largo de su intersección —en los dos puntos verdes de la figura simulada en el lado derecho de la figura 12.5— los pares de fotones tendrán justamente la propiedad requerida.

Animación

Descargando y ejecutando el archivo exe podemos elegir entre tres simulaciones. El primero demuestra la violación de la desigualdad de Bell. El segundo muestra teletransportación cuántica, mientras que el tercero es una realización del protocolo BB84 de distribución de claves cuánticas (QKD) (no discutido aquí).

http://titan.physx.u-szeged.hu/~mmquantum/download.php?download_file=Qmdemo.exe

Los experimentos demostraron unánimemente la validez del resultado mecánico cuántico y la violación de las desigualdades de Bell.