4.5: Ejemplo: Láseres de microchip CW-Q-conmutados de modo único
- Page ID
- 84891
Los láseres de microchip de conmutación Q son láseres de estado sólido compactos y simples, que pueden proporcionar una alta potencia pico con un haz de salida limitado por difracción. Debido a la longitud de cavidad extremadamente corta, típicamente menos de 1 mm, se puede lograr una operación de conmutación Q de frecuencia única con anchos de pulso muy por debajo de ns. Se han demostrado duraciones de pulso de 337 ps y 218 ps con un láser de microchip de conmutación Q pasivamente que consiste en un\(\ce{Nd}: \ce{YAG}\) cristal unido a una fina pieza de\(\ce{Cr}^{4+}: \ce{YAG}\) [8, 9]. Se utilizaron absorbedores semiconductores saturables para conmutar pasivamente un\(\ce{Nd}: \ce{YAG}\) láser monolítico que producía pulsos de 100 ns [38].
Configuración del láser de microchip conmutado pasivamente
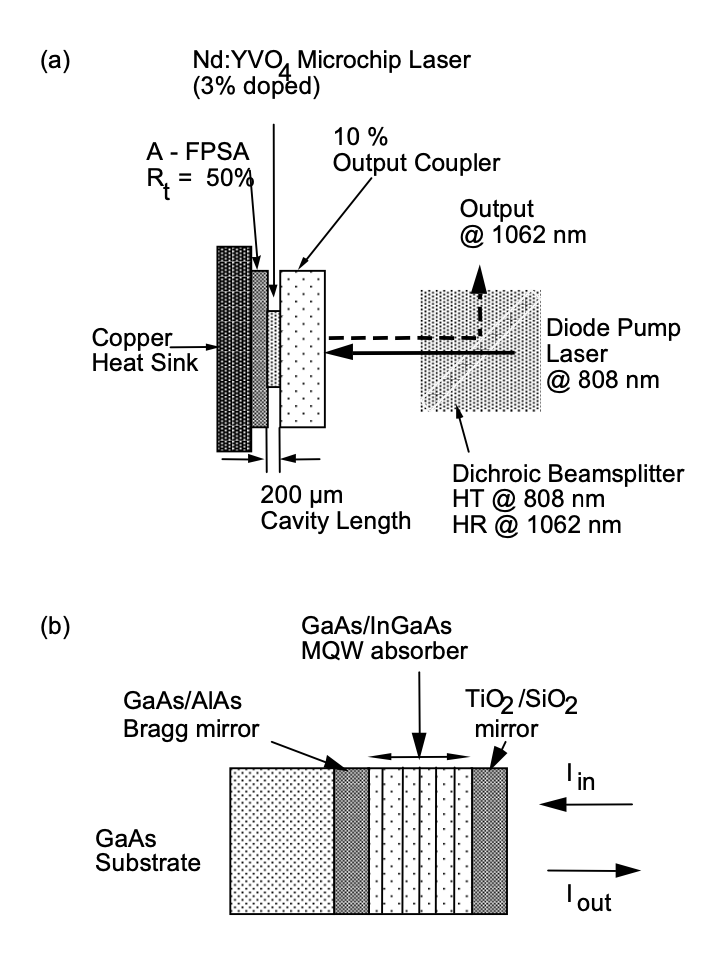
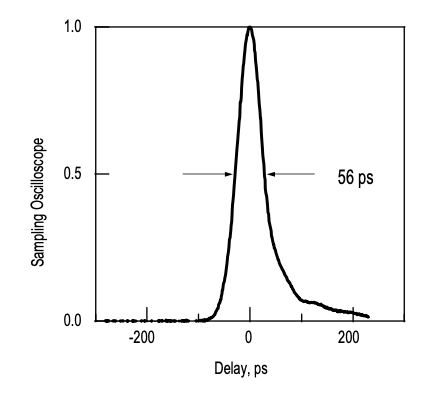
La Figura 4.23 (a) muestra la configuración experimental del láser de microchip conmutado Q pasivamente y la Figura 4.23 (b) la estructura del absorbedor saturable semiconductor [12, 13]. La estructura absorbente saturable es un llamado absorbedor saturable Fabry-Perot antirresonante (A-FPSA), ya que en un láser de microchip el tamaño del haz es fijado por la lente térmica que se acumula en el cristal láser, cuando se bombea con el láser de diodo. Así, se puede usar el reflector superior del A-FPSA para escalar la intensidad de saturación efectiva del absorbedor con respecto a la potencia intracavitaria. El cristal láser de 200\(\ce{Nd}: \ce{YVO4}\) o 220\(\mu\) m de espesor o\(\ce{Nd}: \ce{LaSc3(BO3)4}\), (Nd:LSB) [39] está intercalado entre un acoplador de salida de 10% y el A-FPSA. Este último está recubierto para una alta reflexión a la longitud de onda de bombeo de 808 nm y una reflectividad prediseñada a la longitud de onda del láser de 1.062\(\mu\) m, respectivamente. Los cristales láser son bombeados por un láser de diodo semiconductor a 808 nm a través de un divisor de haz dicroico, que transmite la luz de bombeo y refleja el haz de salida a 1.064 μm para el\(\ce{Nd}: \ce{YVO4}\) o 1.062 μm para el\(\ce{Nd}:\ce{LSB}\) láser. Para obtener pulsos cortos de conmutación Q, la cavidad tiene que ser lo más corta posible. Los cristales láser altamente dopados con una corta longitud de absorción de solo unos 100\(\mu\) m conducen a un láser de microchip corto pero aún eficiente [13]. El absorbedor saturable consiste en un espejo superior dieléctrico y 18 pares de MQW de GaAS/InGaAs cultivados en un espejo GaAS/Alas Bragg. El espesor óptico total del absorbedor es del orden de 1\(\mu\) m, por lo que el incremento de la longitud de la cavidad debido al absorbedor es neglegible. Para más detalles véase [12, 13]. Pulsos tan cortos como 56 ps, Figura (4.24), se han logrado con cristales de Nd: LSB.
Dinámica de un Láser de Microchip Q-Switched
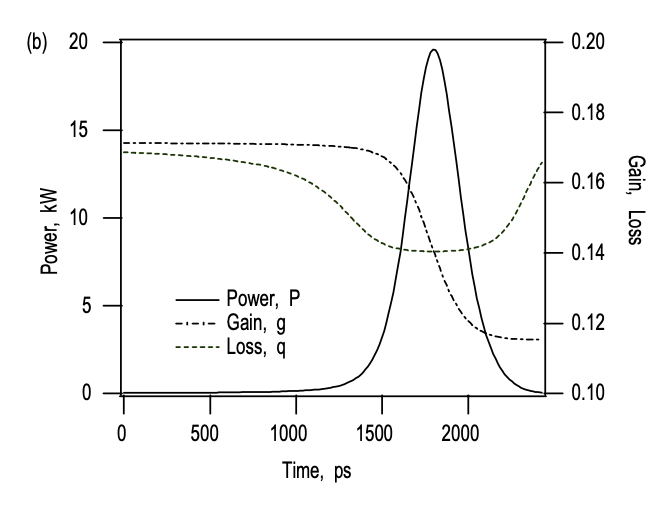
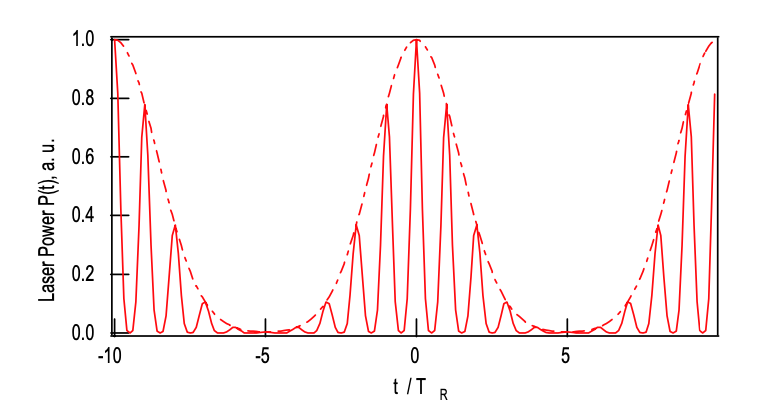
El láser de microchip de conmutación Q pasivamente, mostrado en la Figura 4.23 (a), está perfectamente modelado por las ecuaciones de velocidad (4.4.18) a (4.4.20). Para comprender la dependencia básica de la dinámica de conmutación CW-Q sobre los parámetros del absorbedor, se realizaron simulaciones numéricas del láser de\(\ce{Nd}: \ce{LSB}\) microchip, como se muestra en la Figura 4.23. El conjunto de parámetros utilizado, se da en la Tabla 4.2. Para estos parámetros, obtenemos de acuerdo a la eq. (4.4.24) una fuerza motriz de bloqueo de modo de MDF = 685. Este láser opera claramente en el régimen de conmutación CW-Q tan pronto como el láser se bombea por encima del umbral. Tenga en cuenta que la condición de conmutación Q (4.4.30) solo tiene una validez limitada para el láser de microchip considerado aquí, porque, la longitud de la cavidad es mucho más corta que el tiempo de recuperación del absorbedor. Por lo tanto, la eliminación adiabática de la dinámica del absorbedor ya no está justificada. Las figuras 4.25 y 4.26 muestran la solución numérica del conjunto de ecuaciones de velocidad (4.4.18) a (4.4.20) en una escala de tiempo de microsegundos y una escala temporal de picosegundos cercana a uno de los eventos de emisión de pulsos.
| Parámetro | valor |
| 2\(g_0\) | 0.7 |
| 2\(q_0\) | 0.03 |
| 2\(l\) | 0.14 |
| \(T_R\) | 2.7 ps |
| \(\tau_L\) | 87\(\mu\) s |
| \(\tau_A\) | 24 ps |
| \(E_L\) | 20\(\mu\) J |
| \(E_A\) | 7.7 NJ |
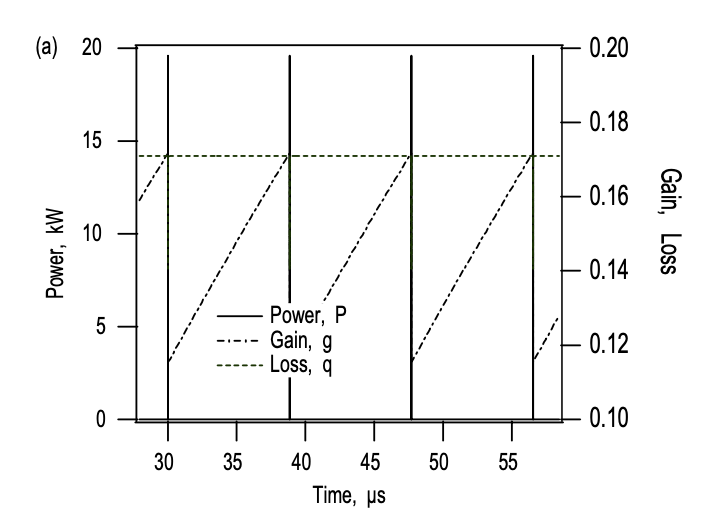
No se conoce ninguna solución analítica para el conjunto de ecuaciones de tasa. Por lo tanto, la optimización de los láseres de conmutación Q tiene una larga historia [4, 5], lo que en general da como resultado criterios de diseño complejos [5], si se considera la solución más general a las ecuaciones de velocidad. Sin embargo, una mirada cuidadosa a los resultados de la simulación conduce a un conjunto de criterios de diseño muy simples, como mostramos a continuación. Como se ve en la Figura 4.25, el tiempo de repetición de pulso\(T_{rep}\) es muchos órdenes de magnitud mayor que el ancho de un pulso de conmutación Q. Así, entre dos emisiones de pulso, la ganancia aumenta debido al bombeo hasta que el láser alcanza el umbral. Esto se describe por la eq. (4.4.19), donde se puede descuidar el plazo de emisión estimulada. Por lo tanto, la frecuencia de repetición de pulso viene determinada por la relación en la que la ganancia tiene que ser bombeada nuevamente al umbral\(g_{th} = l + q_0\), si se satura al valor gf después de la emisión del pulso. En buena aproximación,\(g_f = l - q_0\), siempre y cuando sea una cantidad positiva. Si\(T_{rep} < \tau_L\), se puede linealizar lo exponencial y obtenemos
\[g_{th} - g_f = g_0 \dfrac{T_{rep}}{\tau_L} \nonumber \]
\[T_{rep} = \tau_L \dfrac{g_{th} - g_f}{g_0} = \tau_L \dfrac{2q_0}{g_0}. \nonumber \]
La Figura 4.26 muestra, que la potencia aumenta, porque, el absorbedor satura más rápido que la ganancia. Para obtener una subida rápida del pulso, asumimos un absorbedor que satura mucho más fácil que la ganancia, es decir\(E_A \ll E_L\), y los tiempos de recuperación de ganancia y absorción serán mucho más largos que el ancho del pulso\(\tau_{pulse}\),\(\tau_{A} \gg \tau_{pulse}\). Ya que, asumimos una ganancia lenta y una lenta absorción, podemos descuidar los términos de relajación en eqs. (4.4.19) y (4.4.20) durante el crecimiento y decaimiento del pulso. Luego las ecuaciones para ganancia y pérdida en función de la forma de pulso de conmutación Q desconocida\(f_Q (t)\)
\[P(t) = E_P f_Q (t) \nonumber \]
pueden ser resueltos. La forma\(f_Q (t)\) del pulso vuelve a normalizarse, de tal manera que su integral a lo largo del tiempo es una y\(E_P\) es, por lo tanto, la energía del pulso. Análogamente a la derivación para el umbral de bloqueo del modo Q-switching en eqs. (4.6.3) y (4.6.4), obtenemos
\[q(t) = q_0 \exp \left [ -\dfrac{E_P}{E_A} \int_{-\infty}^{t} f_Q (t') dt' \right ],\label{eq4.5.4} \]
\[g(t) = g_{th} \exp \left [ -\dfrac{E_P}{E_A} \int_{-\infty}^{t} f_Q (t') dt' \right ],\label{eq4.5.5} \]
Sustitución de estas expresiones en la eq. (4.4.18) para la potencia del láser, y la integración sobre el ancho de pulso, determina la energía de pulso extraída. El resultado es un equilibrio entre las pérdidas totales y la ganancia.
\[l + q_P (E_P) = g_P (E_P)\label{eq4.5.6} \]
con
\[q_P (E_P) = q_0 \dfrac{1 - \exp [-\tfrac{E_P}{E_A}]}{\tfrac{E_P}{E_A}}, \nonumber \]
\[g_P (E_P) = g_{th} \dfrac{1 - \exp [-\tfrac{E_P}{E_A}]}{\tfrac{E_P}{E_A}}, \nonumber \]
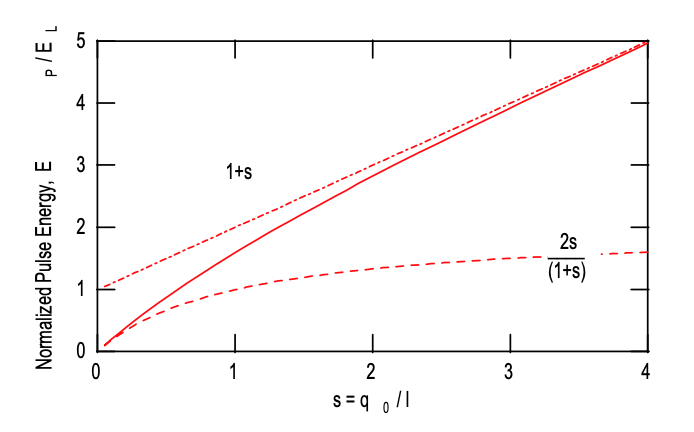
Porque, asumimos que el absorbedor está completamente saturado, podemos establecer\(q_P (E_P) \approx 0\). La Figura 4.27 muestra la solución de la eq. (\(\ref{eq4.5.6}\)), que es la energía del pulso en función de la relación entre pérdidas saturables e insaturables\(s = q_0/l\). También se muestran soluciones aproximadas para pequeñas y grandes s como las curvas discontinuas. Así, cuanto mayor es la relación entre las pérdidas saturables e insaturables, mayor es la energía del pulso intracavitario, lo cual no es sorprendente. Tenga en cuenta que la energía de pulso extraída es proporcional al acoplamiento de salida, que es\(2l\) si no hay otras pérdidas presentes. Si asumimos\(s \ll 1\), entonces, podemos usar aproximadamente la aproximación de baja energía
\[E_P = 2 E_L \dfrac{q_0}{l + q_0}. \nonumber \]
La energía de pulso emitida externamente es dada por
\[E_P^{ex} = 2l E_P = E_L \dfrac{4l q_0}{l + q_0}.\label{eq4.5.10} \]
Así, la energía total extraída del pulso es completamente simétrica en las pérdidas saturables y no saturables. Para una cantidad dada de absorción saturable, la energía de pulso extraída es máxima para un acoplamiento de salida lo más grande posible. Por supuesto, aún debe alcanzarse el umbral, es decir\(l + q_0 < g_0\). Así, en lo siguiente, asumimos\(l > q_0\) como en la Figura 4.26. El absorbedor se blanquea inmediatamente, después de que el láser alcanza el umbral. El campo de luz crece y extrae algo de energía almacenada en el medio de ganancia, hasta que la ganancia se satura al valor de baja pérdida\(l\). Entonces el campo de luz vuelve a decaer, porque la ganancia está por debajo de la pérdida. Durante el decaimiento el campo puede saturar la ganancia en una cantidad similar a la de la acumulación, siempre y cuando las pérdidas saturables sean menores que las pérdidas constantes del acoplador de salida l, lo que asumiremos en lo siguiente. Entonces la forma del pulso es casi simétrica como puede verse en la Figura 4.26 (b) y es bien aproximada por un hiperbolico cuadrado secante por razones que se harán evidentes en un momento. Por lo tanto, asumimos
\[f_Q (t) = \dfrac{1}{2 \tau_P} \text{sech}^2 \left (\dfrac{t}{\tau_p} \right ). \nonumber \]
Con la suposición de una forma de pulso explicita, podemos calcular el ancho de pulso sustituyendo este ansatz en eq. (4.4.18) y usando (\(\ref{eq4.5.4}\)), (\(\ref{eq4.5.5}\))
\[-\dfrac{2T_R}{\tau_P} \tanh \left (\dfrac{t}{\tau_p} \right ) = g_{th} \exp \left [ \right ] - l. \nonumber \]
Nuevamente, descuidamos la absorción saturada. Si ampliamos esta ecuación hasta el primer orden\(E_P/E_L\) y comparamos coeficientes, encontramos a partir del término constante la energía (\(\ref{eq4.5.10}\)), y a partir del término tanh-term obtenemos la siguiente expresión simple para el ancho de pulso
\[\tau_P = 2 \dfrac{T_R}{q_0}. \nonumber \]
Para el ancho de pulso FWHM del\(\text{sech}^2\) pulso resultante obtenemos
\[\tau_{P,FWHM} = 3.5 \dfrac{T_R}{q_0}.\label{eq4.5.14} \]
Así, para el funcionamiento óptimo de un láser de microchip Q-switching, con respecto al ancho de pulso mínimo y la máxima energía extraída en los límites aquí considerados, obtenemos un criterio de diseño muy simple. Si tenemos una ganancia máxima de ida y vuelta de señal pequeña g0, deberíamos diseñar un absorbedor con q0 algo más pequeño que\(g_0/2\) y un acoplador de salida con\(q_0 < l < g_0 - q_0\), para que el láser siga llenando la condición de conmutación CW-Q. Es esta simple optimización, la que nos permitió alcanzar los pulsos más cortos cada uno generado a partir de un láser de estado sólido CW-Q conmutado. Tenga en cuenta, para una absorción saturable máxima de\(2\ q_0 = 13%\), un tiempo de punta redonda de la cavidad de\(T_R = 2.6\) ps para el\(\ce{Nd}: \ce{YVO4}\) láser, se espera de (\(\ref{eq4.5.14}\)) un ancho de pulso de aproximadamente\(\tau_P = 70ps\), que está cerca de lo que observamos en el experimento anterior. Logramos pulsos entre 56 y 90 ps [13]. Las energías de pulso extraídas típicas fueron del orden de\(E_P = 0.1 - 0.2 \mu J\) para pulsos de aproximadamente 60\(ps\) [13]. Usando una energía de saturación de aproximadamente\(E_L = 30\ \mu J\) y una pérdida de acoplador de salida de\(2l = 0.1\), esperamos, según (\(\ref{eq4.5.10}\)), una energía de pulso máxima extraída de\(E_P^{ex} = 2\ \mu J\). Así, tenemos una desviación de un orden de magnitud, lo que indica claramente que el absorbedor todavía introduce demasiadas pérdidas intracavitarias no saturables. La disminución de estas pérdidas debería conducir a\(\mu J\) - pulsos de 50 ps de este tipo de un láser muy simple y barato, en comparación con cualquier otra técnica de generación de pulsos.