5.9: Híbridos
- Page ID
- 80827
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Los híbridos son transformadores que combinan o dividen las señales de microondas entre una serie de entradas y salidas. Se pueden implementar utilizando elementos distribuidos o agrupados y no están restringidos a aplicaciones de RF y microondas. Por ejemplo, un transformador magnético es un híbrido y se puede utilizar para combinar las salidas de dos o más etapas de transistor, o para obtener niveles de impedancia apropiados. Un acoplador\(3\text{ dB}\) direccional basado en líneas acopladas paralelas también es un tipo de híbrido. Las implementaciones específicas se considerarán más adelante en este capítulo, pero por ahora el foco está en sus características idealizadas. Los símbolos comúnmente utilizados para los híbridos se muestran en la Figura 5.8.2.
Un híbrido es un tipo especial de unión de cuatro puertos con la propiedad de que si se aplica una señal en cualquier puerto, emerge de dos de los otros puertos a media potencia, mientras que no hay señal en el cuarto o puerto aislado. Las dos salidas tienen relaciones de fase específicas y todos los puertos coinciden. Sólo se utilizan dos tipos fundamentales de híbridos:\(180^{\circ}\) e\(90^{\circ}\) híbridos. Un híbrido es un tipo de acoplador direccional, aunque el término acoplador direccional, o simplemente acoplador, se usa más comúnmente para referirse a dispositivos donde solo se muestrea una pequeña fracción de la potencia de una señal de entrada. Además, un balun es un tipo especial de híbrido.
5.9.1 Híbrido en cuadratura
El \(90^{\circ}\)híbrido ideal, o híbrido en cuadratura, mostrado en la Figura 5.8.2 (c), tiene los parámetros de dispersión
\[\label{eq:1}S_{90^{\circ}}=\frac{1}{\sqrt{2}}\left[\begin{array}{cccc}{0}&{-\jmath}&{1}&{0}\\{-\jmath}&{0}&{0}&{1}\\{1}&{0}&{0}&{-\jmath}\\{0}&{1}&{-\jmath}&{0}\end{array}\right] \]
La diferencia de\(90^{\circ}\) fase entre los puertos pasante y acoplado se indica por\(−\jmath\). El desplazamiento de fase real, es decir,\(+90^{\circ}\) o\(−90^{\circ}\) (indicado por\(\jmath\)), entre los puertos de entrada y salida depende de la implementación híbrida específica. Otro híbrido en cuadratura podría tener los parámetros
\[\label{eq:2}S_{90^{\circ}}=\frac{1}{\sqrt{2}}\left[\begin{array}{cccc}{0}&{\jmath}&{1}&{0}\\{\jmath}&{0}&{0}&{1}\\{1}&{0}&{0}&{\jmath}\\{0}&{1}&{\jmath}&{0}\end{array}\right] \]
Recordemos el requisito de los moduladores en cuadratura de que el oscilador local se suministre como dos componentes iguales en magnitud pero\(90^{\circ}\) fuera de fase. Un híbrido en cuadratura es solo el circuito que puede hacer esto.
Para convencerte de que Ecuación\(\eqref{eq:2}\) describe una red que divide el poder, considera el flujo de potencia implícito en la Ecuación\(\eqref{eq:2}\). La fracción de potencia transmitida de Puerto\(i\) a Puerto\(j\) es descrita por\(|S_{ji}|^{2}\). Considera la potencia que ingresa a Puerto\(\mathsf{1}\). No se refleja energía para un híbrido ideal, ya que la entrada en Port\(\mathsf{1}\) se corresponde y\(S_{11} = 0\). Puerto\(\mathsf{4}\) debe estar aislado para que no salga energía de Puerto\(\mathsf{4}\), y así\(S_{41} = 0\). La potencia debe dividirse entre Puertos\(\mathsf{2}\) y\(\mathsf{3}\), y estos deben ser iguales a la mitad de la potencia que ingresa a Puerto\(\mathsf{1}\). De la ecuación\(\eqref{eq:2}\),
\[\label{eq:3}|S_{21}|^{2}=\left(\frac{1}{\sqrt{2}}|j|\right)^{2}=\frac{1}{q}\quad\text{and}\quad |S_{31}|^{2}=\left(\frac{1}{\sqrt{2}}|1|\right)^{2}=\frac{1}{2} \]
Así la potencia que ingresa a Puerto\(\mathsf{1}\) se divide, con la mitad yendo a Puerto\(\mathsf{2}\) y la otra mitad a Puerto\(\mathsf{3}\).
5.9.2\(180^{\circ}\) Híbrido
Los parámetros de dispersión del \(180^{\circ}\)híbrido, mostrados en la Figura 5.8.2 (b), son
\[\label{eq:4}S_{180^{\circ}}=\frac{1}{\sqrt{2}}\left[\begin{array}{cccc}{0}&{1}&{-1}&{0}\\{1}&{0}&{0}&{1}\\{-1}&{0}&{0}&{1}\\{0}&{1}&{1}&{0}\end{array}\right] \]
y esto define el funcionamiento del híbrido. En cuanto a las ondas de potencia raíz\(a\) y\(b\), las salidas en los puertos son
\[\label{eq:5}\begin{array}{ll} {b_{1}=(a_{2}-a_{3})/\sqrt{2}}&{b_{2}=(a_{1}+a_{4})/\sqrt{2}}\\{b_{3}=(-a_{1}+a_{4})/\sqrt{2}}&{b_{4}=(a_{2}+a_{3})/\sqrt{2}}\end{array} \]
Las imperfecciones en la fabricación del híbrido resultarán en parámetros de dispersión distintos de cero en los puertos donde idealmente\(S_{ji} = 0\), para que sea mejor terminar
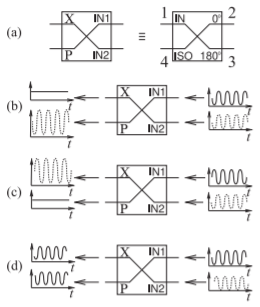
Figura\(\PageIndex{1}\): Un\(180^{\circ}\) híbrido como combinador (con salida en el puerto de suma,\(\sum\)) y como comparador (con salida en el puerto de diferencia\(\Delta\)): (a) equivalencia entre un\(180^{\circ}\) híbrido y un híbrido de suma y diferencia; (b) las dos entradas están en fase; (c) las dos entradas son\(180^{\circ}\) fuera de fase; y d) las dos entradas están\(90^{\circ}\) desfasadas.
el puerto aislado del híbrido, como se muestra en la Figura 5.8.2 (d), para asegurar que no haya señal reflejada (es decir, no\(a_{4}\)) que ingrese al híbrido en el puerto aislado. \(\eqref{eq:5}\)La ecuación muestra que los puertos son intercambiables. Es decir, si se aplica una señal a Port\(\mathsf{3}\), entonces se divide entre Puertos\(\mathsf{1}\) y\(\mathsf{4}\), y Port\(\mathsf{2}\) se convierte en el puerto aislado.
Un híbrido se puede utilizar en aplicaciones distintas de dividir la señal de entrada en un componente pasante y uno acoplado. Un ejemplo de otro uso es en un sistema que combina o compara dos señales, como en la Figura\(\PageIndex{1}\). Aquí se muestra un\(180^{\circ}\) híbrido con los parámetros de dispersión de Ecuación\(\eqref{eq:4}\). Con una señal\(x(t)\) aplicada a Puerto\(\mathsf{2}\) en la Figura 5.8.2 (b), y otra señal\(y(t)\) aplicada a Puerto\(\mathsf{3}\), la salida en Puerto\(\mathsf{4}\) es la señal suma\(x(t) + y(t)\), y la salida en Puerto\(\mathsf{1}\) es la señal de diferencia,\(x(t) − y(t)\). Los nombres más comunes para los puertos de salida (cuando el\(180^{\circ}\) híbrido se usa como combinador) son llamar a Port\(\mathsf{4}\) el puerto sigma o sum, a menudo designado usando el símbolo\(\sum\). Puerto\(\mathsf{1}\) se llama la diferencia o puerto delta,\(\Delta\). Observe que si se aplica una señal al\(\Delta\) puerto generará salidas fuera de fase.
5.9.3 Transformador Magnético Híbrido
En los circuitos híbridos de Figuras\(\PageIndex{2}\) y\(\PageIndex{3}\), el número de devanados de cada bobina (hay tres en cada estructura) es el mismo. Los niveles de impedancia dados son los requeridos para la máxima transferencia de potencia e indican las transformaciones de impedancia de las estructuras. Considerando la figura\(\PageIndex{3}\) y la equiparación de poderes,
\[\label{eq:6}\frac{1}{2}\frac{(2V)^{2}}{Z_{2}}=\frac{1}{2}\frac{V^{2}}{Z_{0}},\quad\frac{4}{Z_{2}}=\frac{1}{Z_{0}}\quad\text{and so}\quad Z_{2}=4Z_{0} \]
Es decir, si\(Z_{2} = 4Z_{0}\), la impedancia que se ve mirando hacia el puerto\(\mathsf{4}\) (del transformador en la Figura\(\PageIndex{3}\)) es\(Z_{0}\), y así el transformador ha proporcionado coincidente con la gran carga. Por ejemplo, si\(Z_{2} = 200\:\Omega\) (quizás la entrada de un transistor), el transformador coincide con esto\(50\:\Omega\).
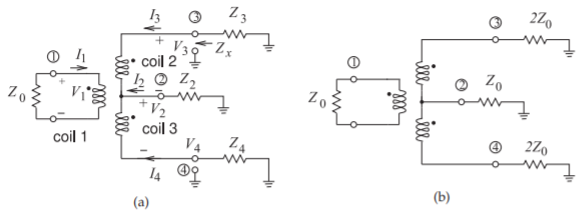
Figura\(\PageIndex{2}\): Transformador magnético híbrido con cada bobina teniendo el mismo número de devanados: (a) mostrando impedancia general de carga; y (b) carga óptima para funcionar como un\(180^{\circ}\) híbrido con Puerto\(\mathsf{2}\) (terminal\(\mathsf{2}\) a tierra) aislado y la entrada balanceada en Puerto\(\mathsf{1}\). Por ejemplo, una antena podría estar conectada a Port\(\mathsf{1}\). Un flujo común pasa a través de las tres bobinas.
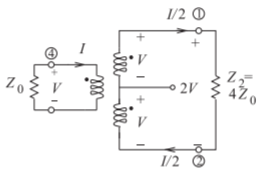
Figura\(\PageIndex{3}\): El transformador magnético de la Figura\(\PageIndex{2}\) como balun transformador de impedancia.
Ejemplo\(\PageIndex{1}\): Magnetic Transformer Hybrid
Considera el híbrido transformador magnético de la Figura\(\PageIndex{2}\) (a) con\(Z_{0}\) real. Determine qué tipo de híbrido es este y calcule las transformaciones de impedancia. Asume el acoplamiento ideal\((k = 1)\).
Solución
Dado que el acoplamiento es ideal y cada bobina tiene el mismo número de devanados,
\[\label{eq:7}(V_{3}-V_{2})=V_{1}\quad\text{and}\quad (V_{2}-V_{4})=V_{1} \]
Los niveles de corriente en el transformador dependen de los circuitos conectados. Para que este circuito funcione como un híbrido con Port\(\mathsf{2}\) aislado, la corriente\(I_{2}\) debe ser cero para que\(I_{3}\) y\(I_{4}\) sean iguales en magnitud pero\(180^{\circ}\) fuera de fase. La carga en Puertos\(\mathsf{3}\) y\(\mathsf{4}\) debe ser la misma. Ahora\(V_{2} = 0,\) desde\(I_{2} = 0,\) y así Ecuación\(\eqref{eq:7}\) convertido
\[\label{eq:8}V_{3}=V_{1}\quad\text{and}\quad V_{4}=-V_{1} \]
por lo que este circuito es un\(180^{\circ}\) híbrido.
Para determinar las condiciones de carga en Puertos\(\mathsf{2,}\)\(\mathsf{3,}\) y\(\mathsf{4}\) se utiliza la siguiente ecuación del transformador:
\[\label{eq:9}V_{3}=\jmath\omega L_{2}I_{3}+\jmath\omega MI_{1}-\jmath\omega MI_{4} \]
donde\(L_{2}\) esta la inductancia de la bobina\(\mathsf{2}\) y\(M\) es la inductancia mutua. Ahora\(I_{1} = −V_{1}/Z_{0},\: L_{2} = L_{3} = M\) ya que el acoplamiento es ideal, y\(V_{3} = V_{1}\). Entonces Ecuación\(\eqref{eq:9}\) se convierte
\[\label{eq:10}V_{3}=\jmath\omega M(2I_{3}-V_{3}/Z-{0})\quad\text{That is,}\quad V_{3}(1+\jmath\omega M/Z_{0})=\jmath 2\omega MI_{3} \]
Si\(\jmath\omega M≫|Z_{0}|,\) esto se reduce a
\[\label{eq:11}Z_{x}=V_{3}/I_{3}=2Z_{0} \]
Para la máxima transferencia de potencia\(Z_{3} = Z_{x}^{\ast}\), pero como\(Z_{0}\) es real,\(Z_{3} = Z_{x} = 2Z_{0}\). De la simetría,\(Z_{4} = Z_{3}\). También,\(I_{3} = −I_{4} = I_{1}/2\).
(El resultado anterior también se puede obtener considerando únicamente consideraciones de transferencia de potencia máxima. El argumento es el siguiente. Se adjunta\(Z_{0}\) una impedancia a la bobina\(\mathsf{1}\). La máxima transferencia de potencia al transformador a través de la bobina requiere que la impedancia de entrada sea\(Z_{0}\) (ya que es real). En la operación híbrida ideal la potencia se divide de manera uniforme entre las potencias entregadas a las cargas en los Puertos\(\mathsf{3}\) y\(\mathsf{4}\), ya que\(V_{1} = (V_{3} − V_{2})=(V_{2} − V_{4})\) y la potencia entregada a la Bobina\(\mathsf{1}\) es\(V_{1}^{2}/(2Z_{0})\). El poder entregado a\(Z_{3}\) (y\(Z_{4}\)) es\((V_{3} − V_{2})^{2}/(2Z_{3}) = V_{1}^{2}/(2Z_{3}) = V_{1}^{2}/(4Z_{0})\). Es decir,\(Z_{3} = 2Z_{0} = Z_{4}\). Es una pequeña extrapolación decir eso\(Z_{3} = 2Z_{0}^{\ast}= Z_{4}\).)
El problema aún no está terminado, como\(Z_{2}\) hay que determinar. Para la operación híbrida, una señal aplicada a Puerto no\(\mathsf{2}\) debe tener respuesta en Puerto\(\mathsf{1}\). Por lo que la corriente en Puerto\(\mathsf{2},\: I_{2},\) debe dividirse entre Bobinas\(\mathsf{2}\) y\(\mathsf{3}\) así eso\(I_{3} = −I_{2}/2 = I_{4}\). Así
\[\label{eq:12}V_{4}=-I_{4}(2Z_{0})=(I_{2}/2)(2Z_{0})=I_{2}Z_{0}=V_{3} \]
Ahora
\[\label{eq:13}V_{3} − V_{2} = V_{1} =0= V_{2} − V_{4},\quad\text{and so}\quad V_{2} = V_{4} = I_{2}Z_{0} \]
Es decir,
\[\label{eq:14}Z_{2}=V_{2}/I_{2}=Z_{0} \]
El circuito\(180^{\circ}\) híbrido final se muestra en la Figura\(\PageIndex{2}\) (b) con las condiciones de carga para la operación emparejada como híbrido.
En el ejemplo anterior se ve que el número de devanados en las bobinas son los mismos de manera que la corriente en Bobinas\(\mathsf{2}\) y\(\mathsf{3}\) (del transformador en la Figura\(\PageIndex{2}\)) es la mitad que en Bobina\(\mathsf{1}\). La regla general es que con un transformador ideal, la suma de los amperios-vueltas alrededor del circuito magnético debe ser cero. La forma precisa de calcular la suma depende de la dirección de los devanados indicada por la convención “punto”. Una generalización de la regla para el transformador que se muestra en la Figura\(\PageIndex{2}\) es
\[\label{eq:15}n_{1}I_{1}-n_{2}I_{2}-n_{3}I_{3}=0 \]
donde\(n_{j}\) esta el numero de devanados de Bobina\(j\) con corriente\(I_{j}\). El ejemplo sirve para ilustrar el tipo de pensamiento detrás del desarrollo de muchos circuitos de RF. Considerar la transferencia máxima de potencia proporcionó una alternativa, inicio más simple para la solución del problema que uno que utilizó las ecuaciones de transformador completo.

