2.3: La línea sin pérdidas terminada

Los ingenieros de microondas quieren trabajar con voltaje y corriente totales cuando sea posible y el arte de la síntesis de diseño generalmente requiere relacionar el voltaje total y el mundo actual de un circuito de elemento agrupado con el mundo de voltaje móvil de las líneas de transmisión. Esta sección desarrolla las importantes abstracciones que permiten que la visión total de voltaje y corriente del mundo sea utilizada con líneas de transmisión. El primer paso en este proceso se encuentra en la Sección 2.3.1 donde los voltajes y corrientes totales están relacionados con el avance y retroceso

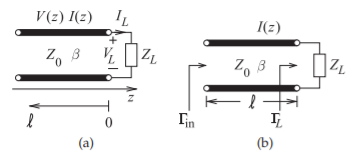
Figura$\PageIndex{1}$: Una línea de transmisión terminada.

voltajes y corrientes de desplazamiento. En la Sección 2.3.2 se presenta una visión de las olas y reflexiones itinerantes. Las abstracciones importantes se presentan primero para el coeficiente de reflexión de entrada de una línea sin pérdidas terminada en la Sección 2.3.3 y luego para la impedancia de entrada de la línea en la Sección 2.3.4. La última sección, Sección 2.3.5, presenta una vista de la tensión total en la línea de transmisión y describe el concepto de onda estacionaria de voltaje.

2.3.1 Voltaje y corriente totales en la línea

Considere la línea terminada que se muestra en la Figura$\PageIndex{1}$ (a). Asumir una onda incidente o de avance, con voltaje de desplazamiento$V_{0}^{+}e^{−\jmath\beta z}$ y corriente$I_{0}^{+}e^{−\jmath\beta z}$ propagándose hacia la carga$Z_{L}$ en$z = 0$. La impedancia característica de la línea de transmisión es la relación de las ondas viajeras de voltaje y corriente de manera que

$$\label{eq:1}\frac{V_{0}^{+}(z)}{I_{0}^{+}(z)}=\frac{V_{0}^{+}e^{-\jmath\beta z}}{I_{0}^{+}e^{-\jmath\beta z}}=\frac{V_{0}^{+}(0)}{I_{0}^{+}(0)}=\frac{V_{0}^{+}}{I_{0}^{+}}=Z_{0}$$

La onda reflejada tiene una relación similar (pero tenga en cuenta el cambio de signo):

$$\label{eq:2}\frac{V_{0}^{-}e^{\jmath\beta z}}{-I_{0}^{-}e^{\jmath\beta z}}=\frac{V_{0}^{-}}{-I_{0}^{-}}=Z_{0}$$

La carga$Z_{L}$ impone una restricción adicional en la relación de la tensión total y la corriente en$z = 0$:

$$\label{eq:3}\frac{V_{L}}{I_{L}}=\frac{V(z=0)}{I(z=0)}=Z_{L}$$

Cuando debe$Z_{L}\neq Z_{0}$ haber una onda reflejada con amplitud apropiada para satisfacer las ecuaciones anteriores. Ahora el voltaje total

$$\label{eq:4}V(z)=V_{0}^{+}e^{-\jmath\beta z}+V_{0}^{-}e^{\jmath\beta z}$$

y la corriente total,$I(z)$, está relacionada con las ondas de corriente circulantes por

$$\label{eq:5}I(z)=\frac{V_{0}^{+}}{Z_{0}}e^{-\jmath\beta z}-\frac{V_{0}^{-}}{Z_{0}}e^{\jmath\beta z}=I_{0}^{+}e^{-\jmath\beta z}+I_{0}^{-}e^{\jmath\beta z}$$

Así, al término de la línea$(z = 0)$,

$$\frac{V(0)}{I(0)}=Z_{L}=Z_{0}\frac{V_{0}^{+}+V_{0}^{-}}{V_{0}^{+}-V_{0}^{-}}\nonumber$$

Esto se puede reorganizar como la relación entre el voltaje reflejado y el voltaje incidente:

$$\frac{V_{0}^{-}}{V_{0}^{+}}=\frac{Z_{L}-Z_{0}}{Z_{L}+Z_{0}}\nonumber$$

Esta relación se define como el coeficiente de reflexión de voltaje en la carga,

$$\label{eq:6}\Gamma_{L}=\Gamma_{L}^{V}=\frac{V_{0}^{-}(0)}{V_{0}^{+}(0)}=\frac{V_{0}^{-}}{V_{0}^{+}}=\frac{Z_{L}-Z_{0}}{Z_{L}+Z_{0}}$$

Es decir, a la carga

$$\label{eq:7}V_{0}^{-}=\Gamma_{L}V_{0}^{+}$$

La relación de las ondas viajeras en la línea también se puede describir utilizando el coeficiente de transmisión$T$ (esta es la letra griega mayúscula tau que se ve igual que la letra inglesa 'T').

El coeficiente de transmisión de voltaje de un puerto en la posición$z$ a un puerto en la posición$0$ es (para la línea de transmisión)

$$\label{eq:8}T=T^{V}=\frac{V_{0}^{+}\text{ (at end of line)}}{V_{0}^{+}\text{ (at start of line)}}=\frac{V_{0}^{+}(0)}{V_{0}^{+}(z)}=\frac{V_{0}^{+}}{V_{0}^{+}e^{-\jmath\beta z}}=e^{\jmath\beta z}$$

La relación en Ecuación se$\eqref{eq:6}$ puede reescribir para que la impedancia de carga de entrada se pueda obtener a partir del coeficiente de reflexión:

$$\label{eq:9}Z_{L}=Z_{0}\frac{1+\Gamma^{V}}{1-\Gamma^{V}}$$

Del mismo modo, el coeficiente de reflexión actual puede escribirse como

$$\label{eq:10}\Gamma^{I}=\frac{I_{0}^{-}}{I_{0}^{+}}=\frac{-Z_{L}+Z_{0}}{Z_{L}+Z_{0}}=-\Gamma^{V}$$

El coeficiente de reflexión de voltaje se utiliza la mayor parte del tiempo, por lo que el coeficiente de reflexión$\Gamma$, por sí solo se refiere al coeficiente de reflexión de voltaje,$\Gamma^{V}=\Gamma$.

Hay varios casos especiales que son dignos de mención. El más importante de estos es el caso cuando no hay onda reflejada y$\Gamma=0$. Para obtener$\Gamma=0$, el valor de impedancia de carga$Z_{L}$, es igual a$Z_{0}$, la impedancia característica de la línea de transmisión como se ve en la Ecuación$\eqref{eq:6}$.

El voltaje total y las ondas de corriente en la línea se pueden escribir como

$$\label{eq:11}V(z)=V_{0}^{+}[e^{-\jmath\beta z}+\Gamma e^{\jmath\beta z}]$$

$$\label{eq:12}I(z)=\frac{V_{0}^{+}}{Z_{0}}[e^{-\jmath\beta z}-\Gamma e^{\jmath\beta z}]$$

A partir de Ecuaciones$\eqref{eq:11}$ y$\eqref{eq:12}$ se puede observar que la tensión y corriente totales en la línea consisten en superposiciones de ondas incidentes y reflejadas.

Ejemplo$\PageIndex{1}$: Forward- and Backward- Traveling Waves at an Open Circuit

Una línea de transmisión sin pérdidas termina en un circuito abierto. ¿Cuál es la relación entre las ondas de voltaje que viajan hacia adelante y hacia atrás al final de la línea?

Solución

Al final de la línea la corriente total es cero, así que eso$I^{+} + I^{−} = 0$ y así

$$\label{eq:13}I^{-}=-I^{+}$$

Los voltajes y corrientes que viajan hacia adelante y hacia atrás están relacionados con la impedancia característica por

$$\label{eq:14}Z_{0}=V^{+}/I^{+}=-V^{-}/I^{-}$$

Observe el cambio en el signo, como resultado del cambio de dirección de propagación pero la referencia positiva para la corriente está en la misma dirección. Sustituyendo por I− en la terminación,

$$\label{eq:15}V^{+}=-V^{-}I^{+}/I^{-}=-V^{-}I^{+}/(-I^{+})=V^{-}$$

Así el voltaje total al final de la línea,$V_{\text{TOTAL}}$, es$V^{+} + V^{−} = 2V^{+}$. Tenga en cuenta que el voltaje total al final de la línea es el doble del voltaje incidente (avance).

Ejemplo$\PageIndex{2}$: Current Reflection Coefficient

Una carga consiste en una conexión de derivación de un condensador de$10\text{ pF}$ y una resistencia de$60\:\Omega$. La carga termina una línea de$50\:\Omega$ transmisión sin pérdidas. La frecuencia de operación es$5\text{ GHz}$.

1. ¿Cuál es la impedancia de la carga?
2. ¿Cuál es la impedancia normalizada de la carga (normalizada a$Z_{0}$ de la línea)?
3. ¿Cuál es el coeficiente de reflexión de la carga?
4. ¿Cuál es el coeficiente de reflexión actual de la carga?

Solución

1. $C = 10\cdot 10^{−12}\text{ F};\: R = 60\:\Omega ;\: f = 5\cdot 10^{9}\text{ Hz};\: \omega = 2πf;\: Z_{0} = 50\:\Omega$
   $$Z_{L} = R||C = (1/R + \jmath\omega C)^{−1} = 0.168 −\jmath 3.174\:\Omega\nonumber$$
2. $z_{L} = Z_{L}/Z_{0} = 3.368\cdot 10^{−3} −\jmath 0.063$.
3. Este es el coeficiente de reflexión de voltaje. $\Gamma_{L} = (z_{L} − 1)/(z_{L} + 1) = −0.985 −\jmath 0.126 = 0.993\angle 187.3^{\circ}$.
4. $\Gamma_{L}^{I} = −\Gamma_{L} = 0.985 +\jmath 0.126 = 0.993\angle (187.3 − 180)^{\circ} = 0.993\angle 7.3^{\circ}$.

2.3.2 Pulsos de desplazamiento hacia adelante y hacia atrás

Las reflexiones al final de una línea producen una señal que viaja hacia atrás. Los pulsos de avance y retroceso se muestran en la Figura$\PageIndex{2}$ (a) para la situación en la que la resistencia al final de la línea es menor que la impedancia característica de la línea$(Z_{L} < Z_{0})$. La fuente de voltaje es un voltaje escalonado que es cero para el tiempo$t < 0$. En el momento$t = 0$, el paso se aplica a la línea y comienza a viajar por la línea, como se muestra en el momento$t = 1$. Este paso de voltaje que se mueve de izquierda a derecha se denomina onda de voltaje de avance.

En el momento$t = 2$, el borde de ataque del escalón alcanza la carga, y como la carga tiene menor resistencia que la impedancia característica de la línea, el voltaje total a través de la carga cae por debajo del nivel del paso de voltaje de avance. La onda reflejada se llama onda que viaja hacia atrás y debe ser negativa, ya que se suma a la onda de avance para producir el voltaje total. De esta manera el coeficiente de reflexión de voltaje$\Gamma$,, es negativo y el voltaje total en la línea, que es todo lo que se puede observar directamente, cae. Una señal de paso reflejada, más pequeña y opuesta viaja en la dirección hacia atrás y se suma al paso de avance para producir la forma de onda que se muestra en$t = 3$. La impedancia de la fuente coincide con la impedancia de la línea de transmisión para que la reflexión en la fuente sea cero. La señal en la línea en el momento$t = 4$, el tiempo para la propagación de ida y vuelta en la línea, por lo tanto, permanece en el valor más bajo. La forma más fácil de recordar la polaridad del pulso reflejado es considerar la situación con un cortocircuito en la carga. Entonces el voltaje total en la línea a la carga debe ser cero. La única forma en que esto puede ocurrir cuando una señal es incidente es si la señal reflejada es igual en magnitud pero opuesta en signo, en este caso$\Gamma = −1$. Entonces cuando sea$|Z_{L}| < |Z_{0}|$, el pulso reflejado tenderá a restar del pulso incidente.

La situación opuesta ocurre cuando la resistencia a la carga es mayor que la impedancia característica de la línea (Figura$\PageIndex{2}$ (b)). En este caso el pulso reflejado tiene la misma polaridad que la señal incidente. Nuevamente, para recordar esto, piense en el caso de circuito abierto. El voltaje a través de la carga se duplica, ya que el pulso reflejado tiene el mismo signo y magnitud que el de la señal incidente, en este caso$\Gamma = +1$. Esto se requiere para que la corriente total sea cero.

Una situación más ilustrativa se muestra en la Figura$\PageIndex{3}$, donde un

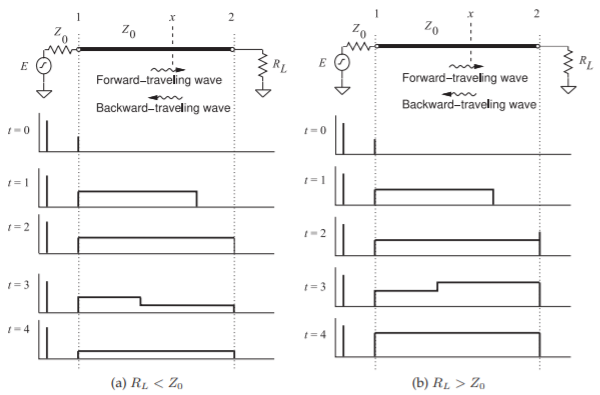
Figura$\PageIndex{2}$: Reflejo de un pulso de voltaje a partir de una carga: (a) cuando la resistencia de la carga,$R_{L}$ es menor que la impedancia característica de la línea,$Z_{0}$ y (b) cuando$R_{L}$ es mayor que$Z_{0}$.

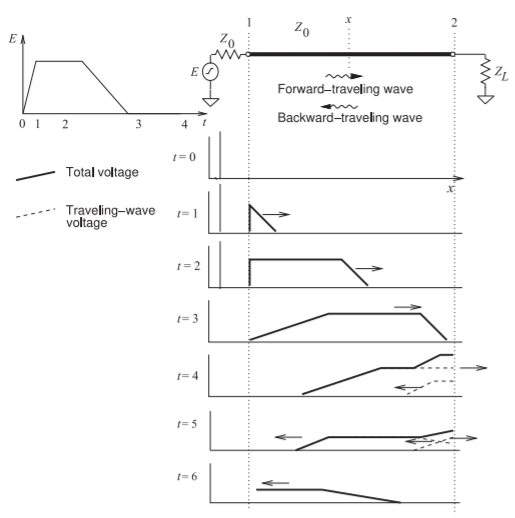
Figura$\PageIndex{3}$: Reflejo de un pulso en una interconexión que muestra pulsos de avance y retroceso. $Z_{L} > Z_{0}$.

señal complicada es incidente sobre una carga que tiene una resistencia superior a la de la impedancia característica de la línea. El pico del voltaje que resulta en la carga es típicamente el objetivo de diseño en muchas interconexiones digitales largas, ya que se necesita transmitir menos energía de señal global por la línea, o equivalentemente se requiere una menor capacidad de accionamiento de corriente de la fuente para lograr la conmutación de primera incidencia. Esto es al precio de tener señales reflejadas en las interconexiones, pero éstas se disipan a través de una combinación de pérdida de línea y absorción de la señal reflejada en el conductor.

2.3.3 Coeficiente de reflexión de entrada de una línea sin pérdidas

El coeficiente de reflexión que mira dentro de una línea varía con la posición a lo largo de la línea a medida que las ondas que viajan hacia adelante y hacia atrás cambian en fase relativa. Haciendo referencia a la Figura$\PageIndex{4}$, a una$\ell$ distancia de la carga (es decir,$z = −\ell$), la entrada

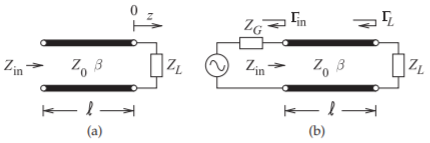
Figura$\PageIndex{4}$: Línea de transmisión terminada: (a) una línea de transmisión terminada en una impedancia de carga,$Z_{L}$, con una impedancia de entrada de$Z_{\text{in}}$; y (b) una línea de transmisión con impedancia de fuente$Z_{G}$ y carga$Z_{L}$.

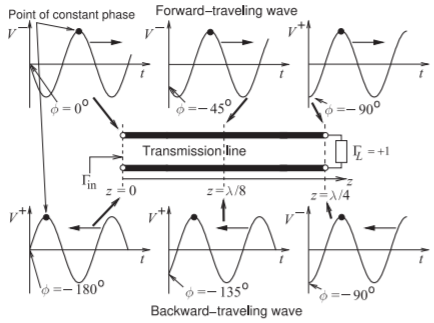
Figura$\PageIndex{5}$: La ola que viaja hacia adelante$v^{+}(t, z) = |V^{+}| \cos(\omega t −\beta z) = |V^{+}| \cos(\omega t + \phi (z))$ y la ola que viaja hacia atrás$v^{−}(t, z) = |V^{+}| \cos(\omega t +\beta z) = |V^{+}| \cos[\omega t + \phi (z)]$. La fase,$\phi$, de la onda de avance se vuelve cada vez más negativa a lo largo de la línea a medida que$z$ aumenta, y cuando se refleja la fase$\phi$ de la onda que viaja hacia atrás se vuelve cada vez más negativa a medida que la ola se aleja de la carga (es decir, a$z$ medida que disminuye).

reflexión mirando en una línea sin pérdidas terminada es

$$\label{eq:16}\Gamma_{\text{in}}|_{z=-\ell}=\frac{V^{-}(z=-\ell)}{V^{+}(z=-\ell)}=\frac{V^{-}(z=0)e^{-\jmath\beta\ell}}{V^{+}(z=0)e^{+\jmath\beta\ell}}=\frac{V^{-}(z=0)}{V^{+}(z=0)}\frac{e^{-\jmath\beta\ell}}{e^{+\jmath\beta\ell}}=\Gamma_{L}e^{-\jmath 2\beta\ell}$$

Tenga en cuenta que$\Gamma_{\text{in}}$ tiene la misma magnitud que$\Gamma_{L}$ pero gira en el sentido de las agujas del reloj (se vuelve cada vez más negativo) al doble de la velocidad de aumento de la longitud eléctrica$\beta\ell$.

Es importante para los conceptos gráficos introducidos posteriormente que haya una apreciación completa del ángulo de$\Gamma_{\text{in}}$ volverse cada vez más negativo al doble de la velocidad a la que aumenta la longitud eléctrica de la línea. La figura$\PageIndex{5}$ es una forma de visualizar esto. La línea de transmisión aquí es$\lambda/4$ larga con una longitud eléctrica de$90^{\circ}$ y termina en una carga con coeficiente de reflexión$\Gamma_{L} = +1$. En$z = 0$ la posición, la onda de voltaje que viaja hacia adelante es$v^{+}(t, 0) = |V^{+}| \cos(\omega t)$, y esto luego se propaga por la línea en la$+z$ dirección. El voltaje de avance en el punto$z = \lambda /8$ en$t = 0$ será el mismo que el voltaje en un$z = 0$ momento de un octavo de período en el pasado. El voltaje en$z =\lambda/8$ es$v^{+}(t, \lambda/8) = |V^{+}| \cos(\omega t − 2π/8)$, es decir, hay una rotación de fase de$−45^{\circ}$. Entonces a$z = \lambda /4$,$v^{+}(t, \lambda/4) = |V^{+}| \cos(\omega t − 2π/4)$, es decir, en el momento$t = 0$ hay una rotación de fase de$−90^{\circ}$ relativa a$v^{+}(0, 0)$, y esta es la negativa de la longitud eléctrica de la línea. La onda de voltaje se refleja en la carga y se convierte en una onda que viaja hacia atrás. Aquí$\Gamma_{L} = +1$ y así, a la carga, la fase de las olas que viajan hacia atrás y hacia adelante son las mismas. La ola que viaja hacia atrás continúa viajando en la$−z$ dirección y su fase en$t = 0$ se vuelve cada vez más negativa a medida$z$ que se acerca a la entrada de la línea. La fase de la onda que viaja hacia atrás en$z = 0$ se gira$−90^{\circ}$ con respecto a la onda que viaja hacia atrás en la carga, y ha girado$−180^{\circ}$ con respecto a la onda que viaja hacia adelante en$z = 0$. Para una línea sin pérdidas, en general, el ángulo de$\Gamma_{\text{in}} = [\text{phase of }V^{−}(z = 0)$ relativo a la fase de$V^{+}(z = 0)] + (\text{the phase of }\Gamma_{L}) = −2(\text{electrical length of the line}) + (\text{the phase of }\Gamma_{L})$.

2.3.4 Impedancia de entrada de una línea sin pérdidas

La impedancia que mira en una línea sin pérdidas varía con la posición, ya que las ondas que viajan hacia adelante y hacia atrás se combinan para producir voltaje y corriente totales dependientes de la posición. A una distancia$\ell$ de la carga (es decir,$z = −\ell$), la impedancia de entrada vista mirando hacia la carga es

$$\label{eq:17}Z_{\text{in}}|_{z=-\ell}=\frac{V(z=-\ell)}{I(z=-\ell)}=Z_{0}\frac{1+|\Gamma|e^{\jmath(\Theta -2\beta\ell)}}{1-|\Gamma|e^{\jmath(\Theta-2\beta\ell)}}=Z_{0}\frac{1+\Gamma_{L}e^{\jmath(-2\beta\ell)}}{1-\Gamma_{L}e^{\jmath(-2\beta\ell)}}$$

Otra forma se obtiene sustituyendo la Ecuación$\eqref{eq:6}$ en la Ecuación$\eqref{eq:17}$:

$$\begin{align}Z_{\text{in}}&=Z_{0}\frac{(Z_{L}+Z_{0})e^{\jmath\beta\ell}+(Z_{L}-Z_{0})e^{-\jmath\beta\ell}}{(Z_{L}+Z_{0})e^{\jmath\beta\ell}-(Z_{L}-Z_{0})e^{-\jmath\beta\ell}}=Z_{0}\frac{Z_{L}\cos(\beta\ell)+\jmath Z_{0}\cos(\beta\ell)}{Z_{0}\cos(\beta\ell)+\jmath Z_{L}\cos(\beta\ell)}\nonumber \\ \label{eq:18}&=Z_{0}\frac{Z_{L}+\jmath Z_{0}\tan\beta\ell}{Z_{0}+\jmath Z_{L}\tan\beta\ell}\end{align}$$

Esta es la ecuación del telégrafo sin pérdidas. La longitud eléctrica,$\beta\ell$, está en radianes cuando se utiliza en los cálculos.

2.3.5 Relación de ondas estacionarias y voltaje de onda estacionaria

El voltaje total en una línea terminada es la suma de las ondas que viajan hacia adelante y hacia atrás. Esta suma produce lo que se llama onda estacionaria. La figura$\PageIndex{6}$ muestra las formas de onda totales y viajeras en una línea terminada en una reactancia y evaluadas en tiempos iguales a múltiplos de un octavo de período. Aquí las ondas viajeras tienen la misma amplitud indicando que la terminación de la línea es reactiva,$|\Gamma| = 1$. La propiedad interesante aquí es que el voltaje total aparece como una onda estacionaria con puntos fijos llamados nodos donde el voltaje total es siempre cero. Esto se ve más fácilmente en la Figura$\PageIndex{7}$ (a), donde el voltaje total se superpone muchas veces. Si la terminación tiene resistencia, entonces la magnitud de la onda que viaja hacia atrás será menor que la de la onda de avance y el voltaje total superpuesto es como se muestra en la Figura$\PageIndex{7}$ (b). Esto sigue siendo una onda estacionaria, pero los mínimos ahora no son cero. La envolvente de esta onda estacionaria se muestra en la Figura$\PageIndex{7}$ (c), donde hay una amplitud máxima$V_{\text{max}}$ y una amplitud mínima$V_{\text{min}}$.

Ahora esta situación será examinada matemáticamente para relacionar la onda estacionaria con el coeficiente de reflexión. Si$\Gamma=0$, entonces la magnitud del voltaje total en la línea,$|V(z)|$, es igual a$|V_{0}^{+}|$ cualquier parte de la línea. Por ello, se dice que tal línea es “plana”. Si hay reflexión la magnitud del voltaje total en la línea no es constante (ver Figura$\PageIndex{7}$ (b)). Así, a partir de Ecuaciones$\eqref{eq:11}$ y$\eqref{eq:12}$:

$$\label{eq:19}|V(z)|=|V_{0}^{+}||1+\Gamma e^{2\jmath\beta z}|=|V_{0}^{+}||1+\Gamma e^{-2\jmath\beta\ell}|$$

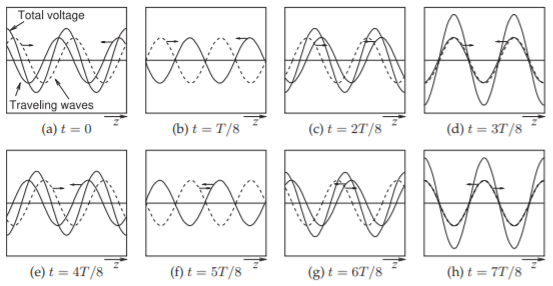
Figura$\PageIndex{6}$: Evolución de una onda estacionaria con carga reactiva como la suma de ondas que viajan hacia adelante y hacia atrás (a la derecha e izquierda, respectivamente) de igual amplitud evaluadas en tiempos$t$ iguales a octavos del periodo$T$. At$t = T/8$ y$t = 5T/8$ el voltaje total en todas partes de la línea es cero.

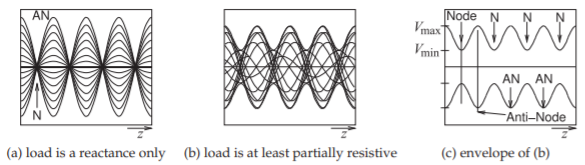
Figura$\PageIndex{7}$: Ondas estacionarias como superposición de formas de onda en muchas ocasiones: (a) cuando las ondas que viajan hacia adelante y hacia atrás tienen la misma amplitud; (b) cuando las ondas tienen diferentes amplitudes; y (c) la envolvente de la onda estacionaria. N es un nodo (un mínimo) y AN es un antinodo (un máximo). Los nodos, N, están separados por$\lambda/2$. Los antinodos, AN, están separados por$\lambda/2$.

donde$z = −\ell$ es la distancia positiva medida desde la carga$z = 0$ hacia el generador. O bien, ajuste$\Gamma = |\Gamma|e^{\jmath\Theta}$,

$$\label{eq:20}|V(z)|=|V_{0}^{+}|\left|1+|\Gamma|e^{\jmath(\Theta-2\beta\ell)}\right|$$

donde$\Theta$ está la fase del coeficiente de reflexión$(\Gamma = |\Gamma|e^{\jmath\Theta})$ en la carga. Este resultado muestra que la magnitud del voltaje oscila con la posición$z$ a lo largo de la línea. El valor máximo se produce cuando$e^{\jmath(\Theta−2\beta\ell)} = 1$ y es dado por

$$\label{eq:21}V_{\text{max}}=|V_{0}^{+}|(1+|\Gamma|)$$

De manera similar, el valor mínimo de la magnitud de voltaje total se produce cuando el término de fase es$e^{\jmath(\Theta−2\beta\ell)} = −1$, y está dado por

$$\label{eq:22}V_{\text{min}}=|V_{0}^{+}|(1-|\Gamma|)$$

Una falta de coincidencia se puede definir por la relación de onda estacionaria de voltaje (VSWR):

$$\label{eq:23}\text{VSWR}=\frac{V_{\text{max}}}{V_{\text{min}}}=\frac{(1+|\Gamma|)}{(1-|\Gamma|)}$$

También

$$\label{eq:24}|\Gamma|=\frac{\text{VSWR}-1}{\text{VSWR}+1}$$

Observe que en general$\Gamma$ es complejo, pero necesariamente$\text{VSWR}$ es siempre real y$1 ≤ \text{VSWR} ≤ ∞$. Para la condición coincidente$\text{VSWR} = 1$,$\Gamma =0$ y, y cuanto más cerca$\text{VSWR}$ esté$1$, más cerca está la carga de coincidir con la línea y más potencia se entrega a la carga. La magnitud del coeficiente de reflexión sobre una línea con una carga de cortocircuito o circuito abierto es$1$, y en ambos casos la$\text{VSWR}$ es infinita.

Para determinar la posición del máximo de onda estacionaria$\ell_{\text{max}}$, considere Ecuación$\eqref{eq:20}$ y anote que al máximo

$$\label{eq:25}\Theta-2\beta\ell_{\text{max}}=2n\pi,\quad n=0,1,2,\ldots$$

Aquí$\Theta$ está el ángulo del coeficiente de reflexión en la carga:

$$\label{eq:26}\Theta-2n\pi =2\frac{2\pi}{\lambda_{g}}\ell_{\text{max}}$$

Así la posición de los máximos de voltaje,$\ell_{\text{max}}$, normalizado a la longitud de onda es

$$\label{eq:27}\frac{\ell_{\text{max}}}{\lambda_{g}}=\frac{1}{2}\left(\frac{\Theta}{2\pi}-n\right),\quad n=0,-1,-2,\ldots$$

De manera similar, la posición de los mínimos de voltaje es (usando la ecuación$\eqref{eq:20}$)

$$\label{eq:28}\Theta-2\beta\ell_{\text{min}}=(2n+1)\pi$$

Después de reorganizar los términos,

$$\label{eq:29}\frac{\ell_{\text{min}}}{\lambda_{g}}=\frac{1}{2}\left(\frac{\Theta}{2\pi}-n+\frac{1}{2}\right),\quad n=0,-1,-2,\ldots$$

Resumiendo a partir de ecuaciones$\eqref{eq:27}$ y$\eqref{eq:29}$:

1. La distancia entre dos máximos sucesivos es$\lambda_{g}/2$.
2. La distancia entre dos mínimos sucesivos es$\lambda_{g}/2$.
3. La distancia entre un máximo y un mínimo adyacente es$\lambda_{g}/4$.
4. A partir$\text{VSWR}$ del medido se$|\Gamma|$ puede encontrar la magnitud del coeficiente de reflexión. A partir$\ell_{\text{max}}$ del medido se$\Gamma$ puede encontrar el ángulo$\Theta$ de. Entonces a partir de$\Gamma$ la carga se puede encontrar la impedancia.

De manera similar a la anterior, la magnitud de la corriente total en la línea es

$$\label{eq:30}|I(\ell)|=\frac{|V_{0}^{+}|}{Z_{0}}\left|1-|\Gamma|e^{\jmath(\Theta-2\beta\ell)}\right|$$

Por lo tanto, la corriente de onda estacionaria es máxima donde la amplitud de voltaje de onda estacionaria es mínima, y mínima donde la amplitud de voltaje de onda estacionaria es máxima.

$Z_{\text{in}}$en Ecuación$\eqref{eq:18}$ es una función periódica de longitud con periodo$\lambda/2$ y varía entre$Z_{\text{max}}$ y$Z_{\text{min}}$, donde

$$\label{eq:31}Z_{\text{max}}=\frac{V_{\text{max}}}{I_{\text{min}}}=Z_{0}\times\text{VSWR}\quad\text{and}\quad Z_{\text{min}}=\frac{V_{\text{min}}}{I_{\text{max}}}=\frac{Z_{0}}{\text{VSWR}}$$

Ejemplo$\PageIndex{3}$: Standing Wave Ratio

En Ejemplo$\PageIndex{2}$ la carga consistió en un condensador de$10\text{ pF}$ en derivación con una resistencia de$60\:\Omega$. La carga terminó una línea de$50\:\Omega$ transmisión sin pérdidas. La frecuencia de operación es$5\text{ GHz}$.

1. ¿Cuál es el$\text{SWR}$?
2. ¿Cuál es la relación actual de onda estacionaria ($\text{ISWR}$)? (Cuando$\text{SWR}$ se utiliza por sí solo se supone que se refiere$\text{VSWR}$.)

Solución

1. De Ejemplo$\PageIndex{2}$$\Gamma_{L} = 0.993\angle 187.3^{\circ}$ y así
   $$\text{VSWR}=\frac{1+|\Gamma_{L}|}{1-|\Gamma_{L}|}=\frac{1+0.993}{1-0.993}=285\nonumber$$
2. $\text{ISWR}=\text{VSWR}=285$

Ejemplo$\PageIndex{4}$: Standing Waves

Una carga tiene una impedancia$Z_{L} = 45 + \jmath 75\:\Omega$ y la impedancia de referencia del sistema,$Z_{0}$, es$100\:\Omega$.

1. ¿Cuál es el coeficiente de reflexión?
2. ¿Cuál es el coeficiente de reflexión actual?
3. ¿Cuál es el$\text{SWR}$?
4. ¿Cuál es el$\text{ISWR}$?
5. La potencia disponible de una fuente con una impedancia equivalente a$100\:\Omega$ Thevenin es$1\text{ mW}$. La fuente está conectada directamente a la carga,$Z_{L}$. Utilice el coeficiente de reflexión para calcular la potencia entregada a$Z_{L}$.
6. ¿Cuál es la potencia total absorbida por la impedancia de fuente equivalente a Thevenin?
7. Discutir el efecto en el flujo de potencia de insertar una línea de$100\:\Omega$ transmisión sin pérdidas entre la fuente y la carga.

Solución

1. El coeficiente de reflexión de voltaje es
   $$\begin{align}\Gamma_{L}&=(Z_{L} − Z_{0})/(Z_{L} + Z_{0}) = (45 +\jmath 75 − 100)/(45 + \jmath 75 + 100) \nonumber \\ &=(93.0\angle (2.204\text{ rads}))/(163.2\angle (0.4773\text{ rads}))\nonumber \\ \label{eq:32} &=0.570\angle (1.726\text{ rads})=0.570\angle 98.9^{\circ} = −0.0881 + \jmath 0.563 = \Gamma^{V} \end{align}$$
2. El coeficiente de reflexión actual es
   $$\label{eq:33}\Gamma^{I}=-\Gamma^{V}=0.0881-\jmath 0.563=0.570\angle (98.9^{\circ} − 180^{\circ})=0.570\angle 81.1^{\circ}$$
3. El$\text{SWR}$ es el$\text{VSWR}$, entonces
   $$\label{eq:34}\text{SWR}=\text{VSWR}=\frac{V_{\text{max}}}{V_{\text{min}}}=\frac{1+|\Gamma^{V}|}{1-|\Gamma^{V}|}=\frac{1+0.570}{1-0.570}=3.65$$
4. La corriente$\text{SWR}$ es$\text{ISWR} = \text{VSWR}$.
5. Para determinar el coeficiente de reflexión de la carga, comience por desarrollar el circuito equivalente Thevenin de la carga. La potencia disponible de la fuente es$P_{A} = 1\text{ mW}$, por lo que el circuito equivalente de Thevenin es
   
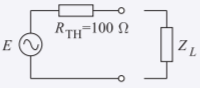
   Figura$\PageIndex{8}$
   La potencia reflejada por la carga es
   $$P_{R} = P_{A}|\Gamma_{L}^{2}| = 1\text{ mW}\cdot (0.570)^{2} = 0.325\text{ mW}\nonumber$$
   y la potencia entregada a la carga es
   $$P_{D}=P_{A}(1-|\Gamma_{L}^{2}|)=0.675\text{ mW}\nonumber$$
6. Es tentador pensar que el poder disipado en$R_{\text{TH}}$ es justo$P_{R}$. Sin embargo, esto no es correcto. En cambio, se$R_{\text{TH}}$ debe determinar la corriente en y luego la potencia disipada en$R_{\text{TH}}$ hallarse. Deje que la corriente$R_{\text{TH}cdot}$ pase$I$, y esto se compone de componentes que viajan hacia adelante y hacia atrás:
   $$I=I^{+}+I^{-}=(1+\Gamma_{I})I^{+}\nonumber$$
   dónde$I^{+}$ está la onda de corriente que viaja hacia adelante.
   $$P_{A}=\frac{1}{2}|I^{+}|^{2}R_{\text{TH}}=\frac{1}{2}|I^{+}|^{2}\times 100=1\text{ mW}=10^{-3}\text{ W}\nonumber$$
   Así así$I^{+} = 4.47\text{ mA}$, y
   $$I = (1 + \Gamma_{I})I^{+} = (1 + 0.0881 −\jmath 0.563)\times 4.47\times 10^{−3}\text{ A},\quad |I| = 5.48\text{ mA}\nonumber$$
   La potencia disipada en$R_{\text{TH}}$ es
   $$\label{eq:35}P_{\text{TH}}=\frac{1}{2}|I|^{2}R_{\text{TH}}=\frac{1}{2}(5.48\times 10^{−3})^{2} R_{\text{TH}} = 1.50\text{ mW}$$
   El circuito es el que se muestra en la parte (e) y así la corriente en$R_{\text{TH}}$ es la misma que la corriente en$Z_{L}$. Así, la potencia entregada a la carga$Z_{L}$ se debe a la parte real de$Z_{L}$:
   $$\label{eq:36}P_{D} =\frac{1}{2}|I|^{2}\Re (Z_{L}) = \frac{1}{2} (5.48\times 10^{−3})^{2}\times 45 = 0.676\text{ mW}$$
7. Insertar una línea de transmisión con la misma impedancia característica que la impedancia equivalente de Thevenin no tendrá ningún efecto sobre el flujo de potencia.

Medición VSWR

La medición de ondas estacionarias se puede utilizar para calcular la impedancia de una carga. El dispositivo que realiza esta medición, denominado línea ranurada, se muestra en la Figura$\PageIndex{9}$ (a). Se inserta una sonda a una pequeña distancia en la línea de transmisión para medir el campo eléctrico. El campo eléctrico de RF produce una tensión de RF en la sonda que es rectificada por el detector de diodos. El voltaje de CC en la salida del detector es proporcional al voltaje total en la línea. La sonda se puede mover a lo largo de la línea y$V_{\text{min}}$ determinar la relación de$V_{\text{max}}$ a. Esto es solo el$\text{VSWR}$. Para encontrar la impedancia de carga compleja también es necesario determinar la posición del nodo de la onda estacionaria. A partir$\text{VSWR}$ del medido se$|\Gamma|$ puede encontrar la magnitud del coeficiente de reflexión. A partir del lmax medido se$\gamma$ puede encontrar el ángulo$\Theta$ de. A partir de$\gamma$ la impedancia de carga se puede encontrar. Esto se demuestra en el siguiente ejemplo.

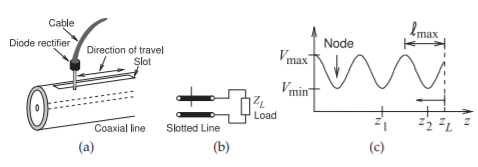
Figura$\PageIndex{9}$: Medición de ondas estacionarias: (a) línea ranurada coaxial; (b) esquema de línea ranurada; (c) onda estacionaria medida.

Ejemplo$\PageIndex{5}$: Slotted Line Measurement of Impedance

Se utiliza una línea ranurada para determinar las propiedades de la onda estacionaria en una$50\:\Omega$ línea terminada ver Figura$\PageIndex{7}$ (c). $V_{\text{max}} = 5\text{ V}$y$V_{\text{min}} = 2\text{ V}$, y el primer mínimo es$2\text{ cm}$ de la carga. La longitud de onda guía es$10\text{ cm}$. ¿Cuál es la impedancia de carga$Z_{L}$?

Solución

Ahora$\text{VSWR} = V_{\text{max}}/V_{\text{min}} = 5/2=2.5$. Entonces, de Ecuación$\eqref{eq:24}$

$$\label{eq:37}|\Gamma|=|\Gamma_{L}|=\frac{\text{VSWR}-1}{\text{VSWR}+1}=\frac{2.5-1}{2.5+1}=0.428$$

La ecuación$\eqref{eq:29}$ y la posición del primer nodo se pueden utilizar para determinar el ángulo de$\Gamma_{L}$. Para el primer nodo (mínimo),$n = 0$ y

$$\label{eq:38}\frac{\ell_{\text{min}}}{\lambda_{g}}=\frac{1}{2}\left(\frac{\Theta}{2\pi}+\frac{1}{2}\right)$$

Reorganizar,

$$\label{eq:39} \Theta=2\pi\left(2\frac{\ell_{\text{min}}}{\lambda_{g}}-\frac{1}{2}\right)\text{ radians}$$

Ahora$\ell_{\text{min}} = 2\text{ cm}$ y$\lambda_{g} = 10\text{ cm}$. Entonces, en grados,

$$\label{eq:40}\Theta=360\left(2\frac{\ell_{\text{min}}}{\lambda_{g}}-\frac{1}{2}\right)=360\left(2\frac{2}{10}-\frac{1}{10}\right)=-36^{\circ}$$

Por lo tanto$\Gamma_{L} = 0.428\angle (−36^{\circ}) = 0.3463 −\jmath 0.2516$, la impedancia de carga es (donde$Z_{0} = 50\:\Omega$)

$$\label{eq:41}Z_{L}=Z_{0}\left(\frac{1+\Gamma_{L}}{1-\Gamma_{L}}\right)=83.2-\jmath 51.3\:\Omega$$

2.3.6 Resumen

Esta sección relacionó la física de las ondas de voltaje y corriente circulantes en líneas de transmisión sin pérdidas con la vista de voltaje y corriente total. Primero se desarrolló el coeficiente de reflexión de entrada de una línea sin pérdidas terminada y a partir de esto se derivó la impedancia de entrada, que es la relación entre el voltaje total y la corriente total. En cualquier punto a lo largo de una línea, la amplitud del voltaje total varía sinusoidalmente, trazando un patrón de onda estacionaria a lo largo de la línea y produciendo la$\text{VSWR}$ métrica que es la relación entre la amplitud máxima del voltaje total y la amplitud mínima de ese voltaje. Esta es una métrica importante que a menudo se usa para proporcionar una indicación de lo buena que es una coincidencia, es decir, qué tan pequeña es la reflexión, con una$\text{VSWR}= 1$ indicación de no reflexión y una reflexión total$\text{VSWR} = ∞$ indicadora, es decir, una magnitud de coeficiente de reflexión de$1$.