2.4: Casos especiales de líneas terminadas sin pérdidas
- Page ID
- 82129
Las configuraciones de línea de transmisión sin pérdidas consideradas en esta sección se utilizan como elementos de circuito en diseños de RF y se utilizan en otras partes de esta serie de libros. El primer elemento considerado en la Sección 2.4.1 es una longitud corta de línea cortocircuitada que parece un inductor. El elemento considerado en la Sección 2.4.2 es una longitud corta de línea de circuito abierto que parece un condensador. Entonces las longitudes de las líneas cortocircuitadas y de circuito abierto, llamadas stubs, utilizadas casi siempre como elementos de derivación para introducir una admitancia en un circuito, se describen en las Secciones 2.4.3 y 2.4.4. Otro tipo de elemento, descrito en la Sección 2.4.5, es un corto tramo de línea con impedancia característica alta o baja realizando un pequeño inductor o condensador en serie respectivamente. El elemento final descrito en la Sección 2.4.6 es un transformador de cuarto de onda, una línea larga de cuarto de longitud de onda con una impedancia característica particular que se utiliza de dos maneras. Se puede usar para proporcionar la máxima transferencia de potencia desde una fuente a una resistencia de carga, y puede invertir una impedancia, por ejemplo, haciendo que un condensador que termina la línea parezca un inductor.
2.4.1 Longitud corta de la línea en cortocircuito
Una línea de transmisión terminada en un cortocircuito (\(Z_{L} = 0\)) tiene la impedancia de entrada (usando la Ecuación (2.3.18))
\[\label{eq:1}Z_{\text{in}}=\jmath Z_{0}\tan(\beta\ell) \]
Así que un corto tramo de línea\(\ell<\lambda_{g}/4\),, parece un inductor con inductancia\(L_{s}\),
\[\label{eq:2}Z_{0}\tan(\beta\ell)=\omega L_{s},\quad\text{and so}\quad L_{s}=\frac{Z_{0}}{\omega}\tan\frac{2\pi\ell}{\lambda_{g}} \]
De la Ecuación\(\eqref{eq:2}\) se puede ver que para un dado\(\ell\),\(L_{s}\) es proporcional a\(Z_{0}\). Por lo tanto, para valores mayores de\(L_{s}\), se necesitan secciones de línea de transmisión de alta impedancia característica. Por lo tanto, las líneas de microcinta con tiras estrechas se pueden usar para realizar inductores en circuitos de microcinta planos.
2.4.2 Largo Corto de Línea Cicuitada Abierta
Una línea de circuito abierto tiene\(Z_{L} = ∞\) y así (usando la ecuación (2.3.18))
\[\label{eq:3}Z_{\text{in}}=-\jmath\frac{Z_{0}}{\tan\beta\ell} \]
Para longitudes\(\ell\) tales que\(\ell < \lambda/4\), un segmento de línea de circuito abierto realiza un condensador\(C_{0}\) para el cual
\[\label{eq:4}\frac{1}{\omega C_{0}}=\frac{Z_{0}}{\tan\beta\ell}\quad\text{and so}\quad C_{0}=\frac{1}{Z_{0}}\frac{\tan(\beta\ell)}{\omega} \]
De la relación anterior, se puede ver que\(C_{0}\) es inversamente proporcional a\(Z_{0}\). Por lo tanto, para valores mayores de\(C_{0}\), es necesario usar secciones de línea de transmisión con baja impedancia característica.
2.4.3 Stub cortocircuitado
Un trozo es una sección de línea de transmisión de circuito abierto o cortocircuitado y se utiliza como elemento en serie o en derivación en un circuito de microondas. Hay varias representaciones. Un trozo cortocircuitado se muestra en la Figura\(\PageIndex{1}\) (a) como una línea de transmisión con impedancia característica\(Z_{01}\) que está cortocircuitada. La impedancia de entrada de la línea es\(Z_{1}\). Si la línea es sin pérdidas, la suposición habitual, entonces\(Z_{01}\) será real y\(Z_{1}\) será imaginaria. Los stubs se usan comúnmente en circuitos de microondas y generalmente todos los stubs en una red tienen la misma longitud, como\(\lambda/4\) largos o\(\lambda/8\) largos. Que se especifica en el diseño. De manera realista no necesitan tener la misma longitud pero hay algunas propiedades especiales para ciertas longitudes, ya que se volverá más claro. En la Figura\(\PageIndex{1}\) (b) se muestra una forma más limpia de indicar un trozo cortocircuitado, donde el valor del talón es como se indica. La ausencia de un\(0\) subíndice (lo que indicaría
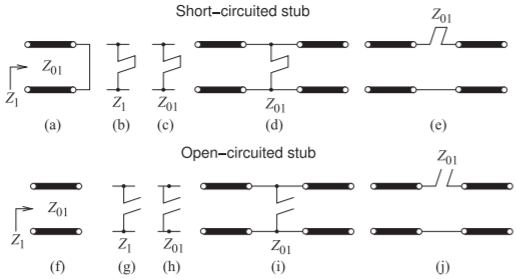
Figura\(\PageIndex{1}\): Talones de línea de transmisión: (a) — (e) talones cortocircuitados; y (f) — (j) talones de circuito abierto.
impedancia característica) significa que esta es la impedancia de entrada reactiva del stub. Si se utiliza un\(0\) subíndice, como en la Figura\(\PageIndex{1}\) (c), se indica la impedancia característica del stub. Si se da un valor numérico entonces una impedancia imaginaria indica que se está especificando la impedancia de entrada, mientras que una impedancia real indica la impedancia característica del stub. El trozo cortocircuitado se muestra como un elemento de derivación en la Figura\(\PageIndex{1}\) (d) y como un elemento en serie en la Figura\(\PageIndex{1}\) (e). Sin embargo, en casi todas las tecnologías de línea de transmisión, incluida la microcinta, solo se pueden realizar los talones de derivación. Los talones de circuito abierto con anotaciones se muestran en las Figuras\(\PageIndex{1}\) (f—j) con asignaciones similares de significado. La longitud de un trozo a menudo se indica por su frecuencia resonante,\(f_{r}\). Esta es la frecuencia a la que el talón es\(\lambda/4\) largo.
El trozo cortocircuitado en la Figura\(\PageIndex{1}\) (a) tiene la impedancia de entrada (de la Ecuación (2.3.18))
\[\label{eq:5}Z_{1}=\jmath Z_{01}\tan\beta\ell \]
donde\(\ell\) está la longitud física de la línea. Dado que el stub es\(\lambda/4\) largo a\(f_{r}\), luego a la frecuencia\(f\), la impedancia de entrada del stub es
\[\label{eq:6}Z_{1}=\jmath Z_{01}\tan\left(\frac{\pi}{2}\frac{f}{f_{r}}\right) \]
Una situación especial, y la más utilizada en el diseño, es cuando la frecuencia de operación es alrededor de la mitad de la frecuencia resonante (es decir,\(f\approx\frac{1}{2}f_{r}\)). Entonces el trozo tiene un octavo de longitud de onda y el argumento de la función tangente en Ecuación\(\eqref{eq:6}\) es aproximadamente\(π/4\) y\(Z_{1}\) se convierte en
\[\label{eq:7}Z_{1}\approx\jmath Z_{01}\tan\left(\frac{\pi}{4}\right)=\jmath Z_{01} \]
realizando así una inductancia\(f = f_{r}/2\) con una reactancia igual a la impedancia característica de la línea.
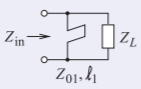
Desarrollar el diseño eléctrico del trozo de derivación mostrado con una carga de impedancia\(Z_{L} = 75 +\jmath 15\:\Omega\) para que la impedancia total de la carga y el trozo sea real.
Figura\(\PageIndex{2}\)
Solución
El trozo cortocircuitado tiene impedancia\(Z_{01}\) y longitud características\(\ell_{1}\). Elija\(Z_{01} = 75\:\Omega\) (generalmente esto debe ser entre\(15\:\Omega\) y\(100\:\Omega\) para la mayoría de las tecnologías de línea de transmisión). El stub necesita ser diseñado para que las susceptancias del stub y la carga sumen a cero. La admisión de la carga\(Y_{L} = 1/Z_{L} = 0.01282 −\jmath 0.002564\text{ S}\). La admisión requerida del talón es\(Y_{\text{STUB}} =\jmath 0.002564\text{ S}\) así, usando Ecuación\(\eqref{eq:5}\),
\[Z_{\text{STUB}}=1/Y_{\text{STUB}}=\jmath Z_{01}\tan\beta\ell_{1}=-\jmath 390\:\Omega\nonumber \]
Por lo tanto, la longitud eléctrica del trozo es
\[\label{eq:8}\beta\ell_{1}=\arctan(-\jmath 390/\jmath 75)=-1.381+n\pi\text{ radians},\:n=0,1,2,\ldots \]
Se toma el primer ángulo positivo para que el trozo tenga la longitud más corta. Entonces
\[\label{eq:9}\beta\ell_{1}=1.761\text{ radians}=100.9^{\circ} \]
El diseño eléctrico completo del trozo es que se trata de una derivación cortocircuitada con una impedancia característica de\(75\:\Omega\) y con una longitud eléctrica de\(100.9^{\circ}\). La impedancia combinada del trozo y la carga es\(Z_{X} = 1/(\Re\{Y_{L}\})=1/0.01282 = 78.00\:\Omega\).
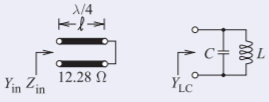
Este ejemplo presenta un enfoque analítico para desarrollar el circuito equivalente de un trozo cortocircuitado en resonancia. Considere una línea de transmisión en cortocircuito con impedancia característica\(Z_{0} = 12.28\:\Omega\) y resonante, es decir, un cuarto de longitud de onda de largo, a\(1850\text{ MHz}\).
Solución
A la primera frecuencia resonante,\(f_{r} =\omega_{r}/(2π)\), la línea de transmisión presenta un circuito abierto y el modelo de circuito apropiado se muestra a la derecha.
Figura\(\PageIndex{3}\)
La estrategia aquí es desarrollar el circuito\(LC\) equivalente equiparando las derivadas del resonador y el\(LC\) circuito. Esto es además de equiparar las admitancias de entrada de los dos circuitos a la frecuencia resonante\(f_{r} = \omega_{r}/(2π)\). Es decir, a la frecuencia\(f_{r}\)
\[\label{eq:10} Y_{\text{in}}(f_{r})=0=Y_{LC}(f_{r})=\jmath[\omega_{r}C-1/(\omega_{r}L)]\quad\text{and so}\quad\omega_{r}^{2}=1/(LC) \]
La impedancia de entrada de la línea a la frecuencia\(f = \omega/(2π)\) es\(Z_{\text{in}}(\omega) = \jmath Z_{0} \tan (\beta\ell)\), y así su admitancia de entrada es
\[\label{eq:11}Y_{\text{in}}(\omega)=\frac{-\jmath}{Z_{0}}\cot(\beta\ell) \]
La derivada de la admisión de la línea de transmisión es (usando la Ecuación (1.A.26))
\[\label{eq:12}\frac{\partial Y_{\text{in}}}{\partial\omega}=\frac{\partial\beta\ell}{\partial\omega}\frac{\partial Y_{\text{in}}}{\partial\beta\ell}=\frac{\partial\beta\ell}{\partial\omega}\left(\frac{-\jmath}{Z_{0}}\right)[-\csc^{2}(\beta\ell)] \]
Ahora\(\beta\) es proporcional a\(\omega\) para una línea sin pérdidas sin dispersión por lo que
\[\frac{\partial Y_{\text{in}}}{\partial\omega}=\frac{\beta\ell}{\omega}\frac{\jmath}{Z_{0}}\csc^{2}(\beta\ell)\nonumber \]
Dado que la línea es aproximadamente\(\lambda/4\) larga cerca de la frecuencia resonante, para\(f\approx f_{r},\:\beta\ell\approx π/2,\: \csc(\beta\ell)\approx 1\) (que es una buena aproximación ya que at\(f_{r}\),\([\partial \csc(\beta\ell)]/(\partial\omega) = 0\)), y
\[\label{eq:13}\left.\frac{\partial Y_{\text{in}}}{\partial\omega}\right|_{\omega_{r}}=\frac{\jmath\beta\ell}{\omega_{r}Z_{0}} \]
La admitancia de entrada del\(LC\) circuito paralelo es
\[\label{eq:14}Y_{LC}=\jmath\left(\omega C-\frac{1}{\omega L}\right)\quad\text{and}\quad\frac{\partial Y_{LC}}{\partial\omega}=\jmath\left( C+\frac{1}{\omega^{2}L}\right) \]
En y cerca de la resonancia\(\omega^{2}\approx 1/(LC)\) y así
\[\label{eq:15}\left.\frac{\partial Y_{\text{LC}}}{\partial\omega}\right|_{\omega_{r}}=\jmath 2C \]
Equiparar las derivadas de\(Y_{\text{in}}\), Ecuación\(\eqref{eq:13}\), y de\(Y_{\text{LC}}\), Ecuación\(\eqref{eq:15}\), rendimientos
\[\label{eq:16}\frac{-\jmath\beta\ell}{\omega Z_{0}}=\jmath 2C \]
Por lo tanto (desde\(\beta\ell\approx\pi/2\))
\[\label{eq:17}C=\frac{\pi}{4\omega_{r}Z_{0}}=\frac{\pi}{4\cdot 2\pi\cdot 1850\cdot 10^{6}\cdot 12.28}=5.502\cdot 10^{-12}\text{ F}=5.502\text{ pF} \]
y, puesto que\(\omega_{r}^{2} = 1/(LC)\),
\[\label{eq:18}L=\frac{1}{\omega_{r}^{2}C}=\frac{1}{(2\pi\cdot 1850\cdot 10^{6})^{2}\cdot 5.502\cdot 10^{-12}}=1.345\cdot 10^{-9}\text{ H}=1.345\text{ nH} \]
2.4.4 Stub de circuito abierto
Una línea de transmisión de circuito abierto se usa comúnmente como un elemento de circuito llamado un trozo abierto que se muestra en la Figura\(\PageIndex{1}\) (f—j). De la Ecuación (2.3.18) y señalando que\(Z_{L} = ∞\), la impedancia de entrada del trozo abierto es
\[\label{eq:19}Z_{1}=-\jmath Z_{01}\frac{1}{\tan\beta\ell} \]
Con el trozo de longitud de onda de un cuarto de longitud de onda a la frecuencia\(f_{r}\), la impedancia de entrada en\(f_{r}\) es un cortocircuito y se dice que el trozo es resonante en\(f_{r}\). Luego, a una frecuencia\(f\), la impedancia de entrada del stub es
\[\label{eq:20}Z_{1}=-\jmath Z_{01}\tan^{-1}\left(\frac{\pi}{2}\frac{f}{f_{r}}\right) \]
Cuando\(f = \frac{1}{2}f_{r}\) el trozo tiene una longitud de onda de un octavo y
\[\label{eq:21}Z_{1}=-\jmath Z_{01}\frac{1}{\tan\left(\frac{\pi}{4}\right)}=-\jmath Z_{01} \]
Entonces un\(\lambda/8\) largo trozo de circuito abierto (\(\lambda/4\)at\(f_{r}\),\(f =\frac{1}{2}f_{r}\)) realiza una capacitancia con una reactancia igual a la impedancia característica de la línea.
Si se puede cambiar la longitud de un trozo, entonces el trozo se puede usar como elemento de afinación. Una técnica común de afinación de microcinta se muestra en la Figura\(\PageIndex{4}\), donde la unión a diferentes almohadillas permite realizar un trozo de longitud variable.
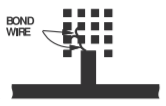
Figura\(\PageIndex{4}\): Stub de circuito abierto con longitud variable realizado mediante unión de alambre desde el trozo fijo a una de las almohadillas de unión. Las almohadillas de unión están en la misma capa que la capa de metal en banda y la unión a ellas se extiende a lo largo del trozo de circuito abierto.
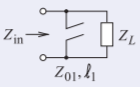
Desarrollar el diseño eléctrico del stub de circuito abierto mostrado con una carga de impedancia\(Z_{L} = 75 +\jmath 15\:\Omega\) para que la impedancia total de la carga y el stub sea real.
Figura\(\PageIndex{5}\)
Solución
El trozo de circuito abierto tiene impedancia\(Z_{01}\) y longitud características\(\ell_{1}\). Una buena opción es elegir\(Z_{01}\) alrededor del nivel de impedancia de la carga siempre y cuando se pueda realizar; así que elija\(Z_{01} = 75\:\Omega\). El stub necesita ser diseñado para que las susceptancias del stub y la carga sumen a cero. La admisión de la carga\(Y_{L} = 1/Z_{L} = 0.01282 −\jmath 0.002564\text{ S}\). La admisión requerida del talón es\(Y_{\text{STUB}} = \jmath 0.002564\text{ S}\), entonces, usando Ecuación\(\eqref{eq:19}\),
\[Z_{\text{STUB}}=1/Y_{\text{STUB}}=-\jmath Z_{01}/\tan\beta\ell_{1}=-\jmath 390\:\Omega\nonumber \]
Por lo tanto, la longitud eléctrica del trozo es
\[\label{eq:22}\beta\ell_{1}=\arctan(\jmath 75/\jmath 390)=0.1900+n\pi\text{ radians},n=0,1,2,\ldots \]
Se toma el primer ángulo positivo para que el trozo tenga la longitud más corta. Entonces
\[\label{eq:23}\beta\ell_{1}=0.1900\text{ radians}=10.89^{\circ} \]
El diseño eléctrico completo del trozo es que es un trozo de derivación de circuito abierto con una impedancia característica de\(75\:\Omega\) y una longitud eléctrica de\(10.89^{\circ}\). La impedancia combinada del trozo y la carga es\(Z_{X} = 1/(\Re\{Y_{L}\})=1/0.01282 = 78.00\:\Omega\).
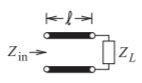
2.4.5 Línea eléctrica corta sin pérdidas
Considere la impedancia de entrada,\(Z_{\text{in}}\), de una línea eléctricamente corta (es decir,\(\beta\ell\) es pequeña) (ver Figura\(\PageIndex{6}\)). Usando la ecuación (2.3.18),
\[\label{eq:24}Z_{\text{in}}\approx\frac{Z_{L}+\jmath Z_{0}(\beta\ell)}{1+\jmath(Z_{L}/Z_{0})(\beta\ell)}\approx [Z_{L}+\jmath Z_{0}(\beta\ell)]\left[1-\jmath\frac{Z_{L}}{Z_{0}}(\beta\ell)\right] \]
Desde\(Z_{0}\beta = \sqrt{L/C}(\omega\sqrt{LC}) = \omega L\) y\(\beta/Z_{0} = (\omega\sqrt{LC})/\sqrt{L/C}) = \omega C\) (donde\(L\) y\(C\) son la inductancia y capacitancia por unidad de longitud de la línea), la ecuación se\(\eqref{eq:24}\) puede escribir como
\[\label{eq:25}Z_{\text{in}}\approx Z_{L}\left[1+(\beta\ell)^{2}\right]+\jmath\left[\omega(L\ell)-Z_{L}^{2}\omega(C\ell)\right] \]
Ya que\(\beta\ell\) es pequeño,\((\beta\ell)^{2}\) es muy pequeño, y así se puede ignorar el\((\beta\ell)^{2}\) término. Entonces la impedancia de entrada de una línea eléctricamente corta terminada en impedancia\(Z_{L}\) es
\[\label{eq:26}Z_{\text{in}}\approx Z_{L}+\jmath[\omega(L\ell)-Z_{L}^{2}\omega(C\ell)] \]
Algunos casos especiales de este resultado serán considerados en los siguientes ejemplos.
Figura\(\PageIndex{6}\): Una línea eléctricamente corta.
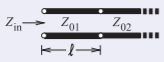
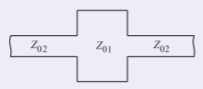
Este ejemplo demuestra que se puede obtener un comportamiento predominantemente capacitivo a partir de un segmento corto de línea de transmisión, la\(Z_{01}\) línea aquí, de baja impedancia característica. Considere el sistema de líneas de transmisión que se muestra a continuación con líneas que tienen las impedancias características,\(Z_{01}\) y\(Z_{02}\),\(Z_{02} ≫ Z_{01}\).
Figura\(\PageIndex{7}\)
El valor de\(Z_{\text{in}}\) es (tratando\(Z_{02}\) como la carga)
\[\label{eq:27}Z_{\text{in}}=Z_{01}\frac{Z_{02}+\jmath Z_{01}\tan\beta\ell}{Z_{01}+\jmath Z_{02}\tan\beta\ell} \]
Ahora\((1 +\jmath x)^{−1}\approx 1 −\jmath x − x^{2}\). Por lo tanto, para una línea corta (y así dejar caer el\(\tan^{2}(\beta\ell)\) término)
\[\label{eq:28}Z_{\text{in}}\approx Z_{02}-\jmath\frac{Z_{02}^{2}}{Z_{01}}\tan(\beta\ell)+\jmath Z_{01}\tan(\beta\ell)=Z_{02}+\jmath Z_{01}\tan(\beta\ell)\left[1-\frac{Z_{02}^{2}}{Z_{01}^{2}}\right] \]
Para\(Z_{02} ≫ Z_{01}\) y para una línea corta,\(\tan(\beta\ell)\approx\beta\ell\), y esto se convierte en
\[\label{eq:29}Z_{\text{in}}\approx Z_{02}-\jmath\frac{Z_{02}^{2}}{Z_{01}}\tan(\beta\ell)\approx Z_{02}-\jmath\frac{Z_{02}^{2}}{Z_{01}}\beta\ell \]
que es capacitivo. Ahora considere el circuito a la derecha donde una capacitancia efectiva\(C_{\text{eff}}\) está en derivación con una carga\(Z_{02}\). Esto tiene la impedancia de entrada
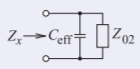
Figura\(\PageIndex{8}\)
\[\label{eq:30}Z_{x}=\left(\jmath\omega C_{\text{eff}}+\frac{1}{Z_{02}}\right)^{-1}=\frac{Z_{02}}{1+\jmath\omega C_{\text{eff}}Z_{02}}=Z_{02}[1-\jmath\omega C_{\text{eff}}Z_{02}-(\jmath\omega C_{\text{eff}}Z_{02})^{2}\ldots \]
Para\(\omega C_{\text{eff}} Z_{02} ≪ 1\) (es decir, una línea eléctricamente corta)
\[\label{eq:31}Z_{x}\approx Z_{02}-\jmath\omega C_{\text{eff}}Z_{02}^{2} \]
Ecuaciones de igualación\(\eqref{eq:29}\) y\(\eqref{eq:31}\), el valor efectivo del condensador de derivación realizado por la longitud corta de la línea de baja impedancia, la\(Z_{01}\) línea, es
\[\label{eq:32}C_{\text{eff}}=\frac{1}{\omega Z_{02}^{2}}\frac{Z_{02}^{2}\beta\ell}{Z_{01}}=\frac{\beta}{\omega}\frac{\ell}{Z_{01}} \]
Por lo tanto, un condensador de derivación se puede realizar aproximadamente mediante una línea de baja impedancia incrustada entre dos líneas de alta impedancia. El diseño de microcinta de esta se muestra en la figura de la derecha. Recordemos que una línea de microcinta ancha tiene una impedancia característica baja.
Figura\(\PageIndex{9}\)
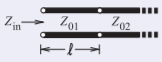
Este ejemplo demuestra que se puede obtener un comportamiento (predominantemente) inductivo a partir de un segmento de línea de transmisión. Considere el sistema de líneas de transmisión que se muestra a continuación con líneas que tienen dos impedancias características diferentes,\(Z_{01}\) y\(Z_{02}\),\(Z_{02} ≪ Z_{01}\).
Figura\(\PageIndex{10}\)
El valor de\(Z_{\text{in}}\) es (usando la Ecuación (2.3.18))
\[\label{eq:33}Z_{\text{in}}=Z_{01}\frac{Z_{02}+\jmath Z_{01}\tan\beta\ell}{Z_{01}+\jmath Z_{02}\tan\beta\ell} \]
que para una línea corta se puede expresar como
\[\label{eq:34}Z_{\text{in}}\approx Z_{02}[1+\tan(\beta\ell)]+\jmath Z_{01}\tan(\beta\ell) \]
Tenga en cuenta que\(\jmath Z_{01}\tan(\beta\ell)\) es la parte dominante para\(\ell < \lambda/8\) y\(Z_{02} ≪ Z_{01}\).
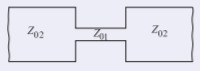
Por lo tanto, una realización de microcinta de un inductor en serie es una línea de alta impedancia incrustada entre dos líneas de baja impedancia. En la figura se muestra una vista superior de dicha configuración en microcinta. Una línea estrecha de microcinta tiene una alta impedancia característica.
Figura\(\PageIndex{11}\)
Los dos ejemplos anteriores mostraron cómo se puede realizar una capacitancia de derivación o inductancia en serie usando secciones cortas de línea, la\(Z_{01}\) línea aquí, con impedancia característica baja o alta respectivamente. Esto permite la realización de algunos circuitos de elementos agrupados en forma de microcinta. En la Figura\(\PageIndex{12}\) (a) se muestra un filtro de paso bajo de elementos agrupados y esto se puede realizar utilizando líneas de microcinta anchas y estrechas, como se muestra en la Figura\(\PageIndex{12}\) (b).
2.4.6 Transformador de cuarto de onda
La figura\(\PageIndex{13}\) (a) muestra una carga resistiva\(R_{L}\) y una sección de línea de transmisión con longitud\(\ell = \lambda_{g}/4\) (de ahí el nombre transformador de cuarto de onda). La entrada
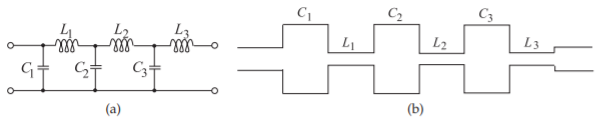
Figura\(\PageIndex{12}\): Un filtro de paso bajo: (a) en forma de red de\(LC\) escalera; y (b) realizado mediante líneas de microcinta.
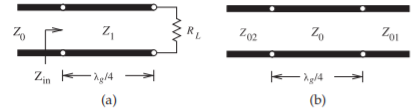
Figura\(\PageIndex{13}\): La línea transformadora de cuarto de onda: (a) transformar una carga; y (b) interconectar dos líneas.
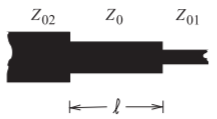
Figura\(\PageIndex{14}\): Disposición de un transformador microcinta de cuarto de onda.
la impedancia de la línea es
\[\label{eq:35}Z_{\text{in}}=Z_{1}\frac{R_{L}+\jmath Z_{1}\tan(\beta\ell)}{Z_{1}+\jmath R_{L}\tan(\beta\ell)}=Z_{1}\frac{R_{L}+\jmath Z_{1}\infty}{Z_{1}+\jmath R_{L}\infty}=\frac{Z_{1}^{2}}{R_{L}} \]
La impedancia de entrada se corresponde con la línea de transmisión\(Z_{0}\) si
\[\label{eq:36}Z_{\text{in}}=Z_{0}^{\ast}=Z_{0} \]
ya que aquí la impedancia característica es real. Por lo tanto
\[\label{eq:37}Z_{1}=\sqrt{Z_{0}R_{L}} \]
y así la línea larga de un cuarto de longitud de onda actúa como un transformador de impedancia ideal.
Otro ejemplo del transformador de cuarto de onda se muestra en la Figura\(\PageIndex{13}\) (b). La impedancia de entrada que mira en el transformador de cuarto de onda (desde la izquierda) viene dada por
\[\label{eq:38}Z_{\text{in}}=Z_{0}\frac{Z_{01}+\jmath Z_{0}\tan(\beta\ell)}{Z_{0}+\jmath Z_{01}\tan(\beta\ell)}=Z_{0}\frac{Z_{01}+\jmath Z_{0}\infty}{Z_{0}+\jmath Z_{01}\infty}=\frac{Z_{0}^{2}}{Z_{01}} \]
De ahí una sección de línea de transmisión de longitud\(\ell = \lambda_{g}/4 + n\lambda_{g}/2\), donde se\(n = 0, 1, 2,\ldots,\) puede utilizar para hacer coincidir líneas que tienen diferentes impedancias\(Z_{02}\),\(Z_{01}\) y, construyendo la línea de manera que su impedancia característica sea
\[\label{eq:39}Z_{0}=\sqrt{Z_{01}Z_{02}} \]
Tenga en cuenta que para una frecuencia central de diseño\(f_{0}\), la sección coincidente proporciona una coincidencia perfecta solo en la frecuencia central y en frecuencias donde\(\ell = \lambda_{g}/4 + n\lambda_{g}/2\).
El diseño de un transformador microcinta de cuarto de onda se muestra en la Figura\(\PageIndex{14}\), donde\(\ell = \lambda_{g}/4\) y la impedancia característica del transformador,\(Z_{0}\), es la media geométrica de las impedancias en cada lado, es decir,\(Z_{0} = \sqrt{Z_{01}Z_{02}}\).
Un transformador de cuarto de onda tiene una propiedad interesante que es ampliamente utilizada. Examine el resultado final en Ecuación\(\eqref{eq:38}\), que se repite aquí:
\[\label{eq:40}Z_{\text{in}}=\frac{Z_{0}^{2}}{Z_{01}} \]
La ecuación\(\eqref{eq:40}\) indica que una línea larga de un cuarto de longitud de onda es un inversor de impedancia que presenta, en el Puerto 1, la inversa de la impedancia presentada en el puerto 2,\(Z_{01}\). Este resultado también se aplica a las impedancias complejas que reemplazan\(Z_{01}\). Esta inversión de impedancia se escala por el cuadrado de la impedancia característica de la línea. Esta inversión se mantiene también en sentido inverso.
2.4.7 Resumen
Las configuraciones de línea de transmisión sin pérdidas consideradas en esta sección son las más utilizadas en el diseño de circuitos de microondas. Es importante tener en cuenta que la línea stub casi siempre se usa en la configuración de derivación para proporcionar una admisión en un circuito. La mayoría de las tecnologías de línea de transmisión, incluyendo líneas coaxiales y microcinta, solo permiten stubs de derivación. El transformador de cuarto de onda es un elemento particularmente interesante que permite la máxima transferencia de potencia desde una fuente a una carga que puede ser diferente. Una característica interesante que es ampliamente explotada es que el transformador de cuarto de onda invierte una impedancia. Por ejemplo, convertir una pequeña resistencia en una resistencia grande, o incluso convertir un condensador pequeño en una inductancia grande. Estas transformaciones son válidas sobre un ancho de banda moderado.