2.5: La Línea Terminada con Pérdida
( \newcommand{\kernel}{\mathrm{null}\,}\)
Anteriormente, la Sección 2.3 presentaba abstracciones que permitían usar una vista de voltaje y corriente total con líneas de transmisión sin pérdidas. Un desarrollo similar se presenta aquí para las líneas con pérdida. Las abstracciones importantes se presentan primero para el coeficiente de reflexión de entrada de una línea con pérdidas terminada en la Sección 2.5.1 y luego para la impedancia de entrada de primero una línea larga con pérdidas en la Sección 2.5.2 y luego para una línea de longitud finita en la Sección 2.5.3. La sección 2.5.4 presenta una aproximación simple para la atenuación en una línea si es de baja pérdida. El flujo de potencia en una línea con pérdidas se considera en la Sección 2.5.5 y luego el impacto de la dispersión en la integridad de la señal se considera en la Sección 2.5.6. La sección final, Sección 2.5.7, describe una técnica para el diseño de una línea sin dispersión de ancho de banda finito.
2.5.1 Coeficiente de reflexión de entrada de una línea con pérdida
Γinde una línea con pérdida se puede desarrollar reemplazandoȷβ en la Sección 2.3.3 porγ. Haciendo referencia a la Figura 2.3.4, a unaℓ distancia de la carga (es decir,z=−ℓ), la reflexión de entrada que mira en una línea con pérdidas hacia la carga es
Γin|z=−ℓ=V−(z=−ℓ)V+(z=−ℓ)=V−(z=0)e−γℓV+(z=0)e+γℓ=V−(z=0)e−γℓV+(z=0)e+γℓ=ΓLe−2γℓ=ΓLe−2αℓe−2ȷβℓ
A medida que la línea se alarga la magnitud deΓin disminuye exponencialmente, acercándose a cero, debido a la atenuación descrita por ele−2αℓ término.
2.5.2 Impedancia de entrada de una línea larga con pérdida
La figura2.5.1 (a) muestra una línea infinitamente larga con impedancia característicaZ0. La impedanciaZin de entrada de la línea es la relación entre el voltajeV1 total y la corriente totalI1 en la entrada de la línea:
Zin=V1I1
Si la línea es infinitamente larga o con pérdidas suficientes, hay una onda reflejada insignificante y, por lo tanto, el voltaje y la corriente totales son solo los que viajan hacia adelante
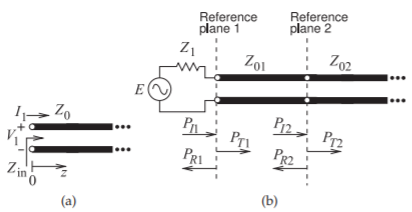
Figura2.5.1: Redes de líneas de transmisión: (a) una línea infinitamente larga; y (b) con una línea de longitud finita de impedancia característicaZ01 y una línea de transmisión infinitamente larga de impedancia característicaZ02.
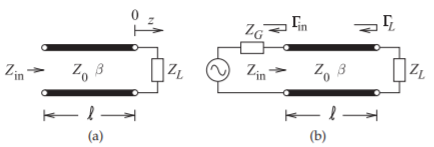
Figura2.5.2: Línea de transmisión terminada: (a) una línea de transmisión terminada en una impedancia de carga,ZL, con una impedancia de entrada deZin; y (b) una línea de transmisión con impedancia de fuenteZG y cargaZL.
voltaje y corriente y
Zin=V1I1=V+(0)I+(0)=Z0
La línea infinitamente larga se aproxima por un cable muy largo, ligeramente con pérdidas. No importará cómo termine la línea (por ejemplo, en una resistencia, circuito abierto o cortocircuito), habrá una onda despreciable que viaja hacia atrás y la impedancia de entrada del cable será su impedancia característica.
2.5.3 Impedancia de entrada de una línea con pérdida
La impedancia que mira dentro de la línea varía con la posición, ya que las ondas de avance y retroceso se combinan para producir voltaje y corriente totales dependientes de la posición. A una distanciaℓ de la carga (es decir,z=−ℓ), la impedancia de entrada vista mirando hacia la carga es
Zin|z=−ℓ=V(z=−ℓ)I(z=−ℓ)=Z01+|Γ|e(ȷΘ−2γℓ)1−|Γ|e(ȷΘ−2γℓ)=Z01+ΓLe−2γℓ1−ΓLe−2γℓ
Otra forma proviene de sustituir la Ecuación (2.3.6) en la Ecuación(???):
Zin=Z0(ZL+Z0)eγℓ+(ZL−Z0)e−γℓ(ZL+Z0)eγℓ−(ZL−Z0)e−γℓ=Z0ZLcosh(γℓ)+ȷZ0cosh(γℓ)Z0cosh(γℓ)+ȷZLcosh(γℓ)=Z0ZL+Z0tanhγℓZ0+ZLtanhγℓ
Esta ecuación también se conoce como la ecuación del telégrafo con pérdida.
Tenga en cuenta queZin es una función cuasi-periódica deℓ y se acercaZ0 para una línea larga con pérdida (es decir, siempre que haya atenuación y la líneaγ tenga una parte real como luegotanhγℓ va a una).
Una línea en cortocircuito se utiliza como resonador. La primera resonancia es una resonancia paralela a1 GHz.
- Dibuje el circuito equivalente de elementos grumados del resonador.
- ¿Cuál es la impedancia que mira dentro de la línea en la resonancia?
- ¿Cuál es la longitud eléctrica del resonador?
- Si el resonador esλg/4 más largo, ¿cuál es la impedancia de entrada del resonador ahora?
Solución
-
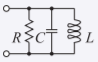
La figura2.5.3
LC es un circuito abierto en resonancia. Si la línea es sin pérdidas,R=0. - Zin=∞(para una línea sin pérdidas).
- De la Ecuación (2.3.18) y conZL=0,Zin=ȷZ0tan(βℓ). Zin=∞cuándotan(βℓ)=∞, es decir, cuándoβℓ=π/2=λg/4=90∘.
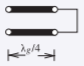
Figura2.5.4 - Zin=0Ω
2.5.4 Atenuación en una línea de baja pérdida
Recordemos queγ, la constante de propagación, viene dada por
γ=√(R+ȷωL)(G+ȷωC)
Esto se puede escribir como
γ=ȷω√LC√(1+RȷωL)(1+GȷωC)
Con una línea de baja pérdidaR≪ωL yG≪ωC, y así, usando una aproximación de la serie Taylor (ver Ecuación (1.A.88)),
(1+RȷωL)1/2≈1+12RȷωL
y
(1+GȷωC)1/2≈1+12GȷωC
así
γ≈12(R√CL+G√LC)+ȷω√LC
Por lo tanto, para líneas de baja pérdida (enNp/m si se utilizan unidades SI),
α≈12(RZ0+GZ0)
y
β≈ω√LC
Lo que(???) indica la Ecuación es que para las líneas de baja pérdida la constante de atenuaciónα,, consiste en partes relacionadas con dieléctricas y conductoras; es decir,
α=αd+αC
αd≈GZ0/2
y
αc≈R/(2Z0)
dondeαd es la atenuación aportada por la pérdida dieléctrica y se llama atenuación dieléctrica, yαd es la atenuación aportada por la pérdida del conductor y se llama atenuación óhmica o conductora.
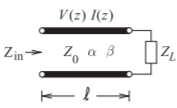
Figura2.5.5: Una línea de transmisión de baja pérdida. La constante de propagaciónγ=α+ȷβ.
2.5.5 Flujo de energía en una línea con pérdida terminada
En esta sección se considera una línea de transmisión con pérdida baja de manera queR≪ωL yG≪ωC, y la impedancia característica esZ0≈√L/C. La figura2.5.5 es una línea de transmisión con pérdidas y el voltaje y la corriente totales en cualquier punto de la línea están dados por
V(z)=V+0[e−γz+Γeγz]andI(z)=V+0Z0[e−γz−Γeγz]
La Sección 2.5.3 derivó la ecuación del telégrafo con pérdida:
Zin=Z0ZL+Z0tanhγℓZ0+ZLtanhγℓ
Para una línea de transmisión con pérdidas, no toda la potencia aplicada en la entrada se entregará a la carga ya que la energía se perderá en la línea debido a la atenuación. La potencia entregada a la carga (que está en la posiciónz=0) es
PL=12R{V(0)I∗(0)}=|V+0|22Z0(1−|ΓL|2)
dondeΓL está el coeficiente de reflexión de la carga. Del mismo modo la potencia en la entrada de la línea (en la posiciónz=−ℓ) es
Pin=12ℜ{V(−ℓ)I∗(−ℓ)}=|V+0|22Z0[1−|ΓL|2e−4αℓ]e2αℓ
y el poder perdido en la línea es
Ploss=Pin−PL=|V+0|22Z0[(e2αℓ−1)+|ΓL|2(1−2−2αℓ)]
La energía se almacena en una línea de transmisión y esto debe considerarse al derivar elQ de un resonador de línea de transmisión. Consideremos la línea de transmisiónλ/4 - larga y cortocircuitada examinada en los Ejemplos 2.3.1 y 2.4.2. Esta línea tiene una impedancia característica de12.28Ω, es resonante en1850 MHz, y una10 kΩ resistenciaR, está en la entrada como se muestra en la figura izquierda.
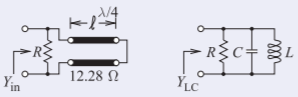
Figura2.5.6
Solución
En resonancia
Q=2πPeak energy storedEnergy dissipated per cycle=ωrPeak energy storedPower loss in the resistorQ=1/(Fractional bandwidth)
dondeωr está la frecuencia del radián en la resonancia. Entonces, hay dos formas fundamentales en las que seQ puede determinar: determinar la energía máxima almacenada y la pérdida de potencia, y encontrar el ancho de banda fraccional. Sin embargo, usar el ancho de banda fraccional es solo un método aproximado, al igualQ que una medida de la energía almacenada y la energía disipada.
Para unRLC resonador de elementos grumosos
Q={1R√LC=ωrLRfor a series RLC circuitR√CL=ωrCGfor a shunt RLC circuit
El circuito equivalente de elementos grumosos de banda estrecha del resonador desarrollado en el Ejemplo 2.3.1, conC=5.503 pF yL=1.345 pH puede ser utilizado. Así
Q=R√CL=10⋅103√5.503⋅10−121.345⋅10−9=640
Es importante señalar que la impedancia de entrada de la línea de transmisión a la frecuencia resonante no se puede utilizar para encontrar el resonadorQ de la línea de transmisión, ya que no transmite ninguna información sobre la energía almacenada. Sin embargo, el modelo de banda estrecha del resonador en resonancia sí captura la información de almacenamiento de energía y por lo tanto se puede utilizar para calcular laQ del resonador, como se hizo aquí.
2.5.6 Dispersión de línea de transmisión con pérdida
En una línea con pérdidas, la velocidad de fase, la velocidad de grupo y la constante de atenuación dependen de la frecuencia y, por lo tanto, una línea con pérdidas es, en general, dispersiva. Es decir, diferentes componentes de frecuencia de una señal viajan a diferentes velocidades, y la velocidad de fasevp, y la velocidad de grupovg, son funciones de frecuencia. En consecuencia, la señal se extenderá en el tiempo y, si la línea es lo suficientemente larga, será difícil extraer la información original.
En el apartado anterior se vio, en Ecuación(???), que para una línea TEMω/β=vp=vg es aproximadamente independiente de la frecuencia para una línea de baja pérdida. Esto es cierto para la mayoría de las líneas de dos conductores (líneas que admiten modos TEM), pero no para todas las estructuras de líneas de transmisión que guían las ondas EM (una guía de ondas rectangular es un ejemplo de dóndevg yvp difieren significativamente). Además, el componente conductor de la constante de atenuación,αc en la Ecuación(???), es aproximadamente independiente de la frecuencia. Sin embargo, el componente dieléctrico,αd en Ecuación(???), depende de la frecuencia incluso para una línea de baja pérdida. EstoG se debe principalmente a la pérdida de energía cuando un entramado material o componentes moleculares son distorsionados por elE campo. Por lo que hay más pérdida yG aumenta linealmente a medida que aumenta la frecuencia. (La conductividad del dieléctrico también afectaG, pero este suele ser un efecto mucho menor a excepción de un sustrato de silicio). Si la línea de transmisión tiene una pérdida moderada, todos los parámetros de propagación dependerán de la frecuencia y la línea es dispersiva.
2.5.7 Diseño de una Línea Perdida sin Dispersión
A lo largo de un ancho de banda moderado, se puede diseñar una línea con pérdidas para que no tenga dispersión (es decir,vg≈vp≈ constante). Los parámetros que son importantes para describir la propagación de la señal en una línea de transmisión son la constante de propagaciónγ, y la impedancia característica,Z0. Al considerar la dispersión es más apropiado examinarα yvp≈ω/β (para una línea de baja pérdida), ya que estos parámetros son generalmente dependientes de la frecuencia para una línea con pérdidas. Para que una línea sea sin dispersiónα,ω/β, yZ0 debe ser independiente de la frecuencia.
Para cualquier línea de baja pérdida, la constante de propagación es
γ=√(R+ȷωL)(G+ȷωC)=ȷω√LC[(1+RȷωL)(1+GȷωC)]1/2
Si la línea está diseñada de manera que
R/L=G/C
entonces
γ=α+ȷβ=ȷω√LC(1+RȷωL)=R√CL+ȷω√LC
A partir de esto
α=R√CL,β=ω√LC and vp=ω/β=1/√LC
El análisis se completa considerando la impedancia característica
Z0=√R+ȷωLG+ȷωC=√LC√R/L+ȷωG/C+ȷω
y, refiriéndose a la Ecuación(???), señalar que el último término de raíz cuadrada es1, entonces
Z0=√L/C
que es independiente de la frecuencia. Las características importantes que describen la propagación de la señal son ahora independientes de la frecuencia y la línea no tiene dispersión. En la práctica, una línea sin dispersión con pérdidas solo puede aproximarse sobre un ancho de banda pequeño ya queG depende linealmente de la frecuencia debido a la dependencia de frecuencia de la pérdida de relajación dieléctrica.
2.5.8 Resumen
Una sección anterior desarrolló el coeficiente de reflexión de entrada y la impedancia de entrada de una línea sin pérdidas. Esta sección hizo lo mismo pero por una línea con pérdidas. Se presentaron derivaciones de mano corta para la atenuación de una línea de baja pérdida en términos de resistencia por unidad de longitud e impedancia característica de la línea. Se discutió la dispersión en una línea y se presentó una técnica de diseño para el diseño de una línea sin dispersión. Este diseño es válido sobre un ancho de banda estrecho o moderado y esta limitación de ancho de banda se aplica a todos los diseños basados en líneas de transmisión.


