2.6: Reflexiones en las interfaces
( \newcommand{\kernel}{\mathrm{null}\,}\)
Las líneas de transmisión transfieren energía de un punto a otro y a menudo hay muchas interfaces en las que se refleja y transfiere la energía. Esta sección se centra en desarrollar una comprensión intuitiva de la reflexión y transmisión de potencia en interfaces y sobre una línea de transmisión. La Sección 2.6.1 presenta una comprensión del flujo de potencia e introduce el concepto de pérdida de retorno aplicando este análisis a una única interfaz en la Sección 2.6.3. La ingeniería de microondas está muy preocupada por la máxima transferencia de potencia y el análisis que respalda las opciones de diseño, el teorema de transferencia de potencia máxima, se revisa en la Sección 2.6.2. La Sección 2.6.4 presenta el análisis del diagrama de rebote que se refiere a la reflexión y transmisión en múltiples interfaces. Esto puede ser un análisis confuso pero proporciona la comprensión esencial para el desarrollo de la intuición sobre cómo fluye el poder, y la comprensión de situaciones en las que el flujo de energía puede ser interrumpido. La sección final, Sección 2.6.5, presenta la teoría de las pequeñas reflexiones, derivada del análisis del diagrama de rebote, que se utiliza en varios lugares de esta serie de libros en la síntesis de redes de líneas de transmisión.
2.6.1 Flujo de potencia y pérdida de retorno
Ahora considere el flujo de potencia en la línea sin pérdidas en la Figura 2.3.1. La onda incidente (que viaja hacia adelante) tiene el poder
P+=12ℜ[V+(I+)∗]=12ℜ[V+(V+Z0)∗]=12ℜ{(V+0e−ȷβz)(V+0e−ȷβzZ0)∗}=12|V+0|2Z0
y la onda reflejada tiene la potencia (usando la Ecuación (2.3.7))
P−=12|V−0|2Z0=|Γ|22|V+0|2Z0
Considerando la conservación de la energía, la potencia entregada a la cargaPL,, es la diferencia de las potencias que viajan hacia adelante y hacia atrás:
PL=12ℜ{VLI∗L}=P+−P−=P+(1−|Γ|2)
Los casos notables son cuando hay un circuito abierto, un cortocircuito o una carga puramente reactiva al final de una línea de transmisión. Estos tienen|Γ|=1. Así todo el poder se refleja de nuevo a la fuente yPL=0.
La potencia que es absorbida por la carga aparece como una pérdida en lo que respecta a las ondas incidentes y reflejadas. Para describir esto, se introduce el concepto de pérdida de retorno (RL) y se define como
RL=−20log|Γ| dB
RL indica la potencia disponible no entregada a la carga. Una carga emparejada(Γ=0) tieneRL=∞ dB, y una reflexión total(|Γ|=1) tieneRL=0 dB.
Una línea de transmisión con una impedancia característica de75Ω soporta una onda de avance con una potencia de1μW. La línea se termina en una resistencia de100Ω. Dibuje el circuito equivalente a elementos grumados en la interfaz entre la línea de transmisión y la carga.
Solución
El circuito equivalente tiene la forma
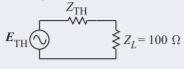
Figura2.6.1
dondeETH es el generador equivalente a Thevenin yZTH es la impedancia del generador equivalente a Thevenin.
La amplitud de la onda de voltaje de avance se obtiene calculando la potencia en la onda de avance:
P+=12(V+)2/Z0=(V+)2/150=1μW=10−6 W
EntoncesV+=√150⋅10−6=12.25 mV. Tenga en cuenta que no loV+ esETH. Para calcularETH, considera el circuito a la derecha que da como resultado la máxima transferencia de potencia.
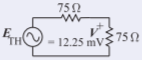
Figura2.6.2
EntoncesETH=2V+=24.5 mV. Dado que la línea tiene una impedancia característica de75Ω, entoncesZTH=75Ω. Entonces, el circuito equivalente a elementos grumados a la carga es
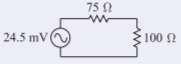
Figura2.6.3
2.6.2 Teorema de transferencia de potencia máxima
Muchos cálculos de líneas de transmisión se pueden resolver utilizando los conceptos de potencia máxima disponible, potencia incidente y potencia reflejada. A frecuencias de microondas la impedancia de salida de las fuentes, por ejemplo, no puede ignorarse como a menudo se puede hacer a bajas frecuencias. Así, la salida de una fuente de RF se define en términos de potencia máxima disponible.
Considere la fuente que se muestra en la Figura2.6.4 con una impedancia queZS=RS+ȷXS impulsa una cargaZL=RL+ȷXL. El objetivo aquí es encontrarZL para la entrega máxima de potencia a la carga. La corriente fasora en la carga es
I=EZS+ZL
y así la potencia promedio en la carga es
PL=12|I|2RL=12(|E||ZS+ZL|)2RL=12|E|2RL(RS+RL)2+(XS+XL)2
La carga requerida para la transferencia máxima de potencia se obtiene considerando primero un valor fijo deRL y luego encontrando el valor deXL requerido para minimizar
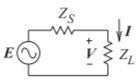
Figura2.6.4: Una fuente terminada en una carga. La transferencia máxima de potencia ocurre cuandoZL=Z∗S.
Ecuación(???). Dado queXL sólo afecta el denominador en la Ecuación(???), es claro que el denominador se minimiza haciendoXL=−XS. Así que ahora Ecuación se(???) reduce a
PL=12|E|2RL(RS+RL)2
y
PL=12|E|2(R2S/RL+2RS+RL)
Ahora la potencia entregada a la carga se maximiza minimizando el denominador en la Ecuación(???), lo que ocurrirá cuando la derivada del denominador en Ecuación(???) sea cero. Es decir, cuando
ddRL(R2S/RL+2RS+RL)2=−R2SR2L+1=0
La derivada es cero cuando
R2S/R2L=1,that is, whenRL=±RS
Cuando la derivada es cero, la potencia transferida a la carga es la potencia mínima o máxima que se puede entregar a la carga. ClaramenteRL=−RS es una solución sin sentido ya que la resistencia de carga y fuente debe ser positiva. Además, hay que comprobar las situaciones en los extremos, es decir, cuandoRL es muy pequeñoRL→0, y cuandoRL es muy grande,RL→∞. AsRL→0, Ecuación(???) se conviertePL→0, y comoRL→∞, Ecuación(???) se conviertePL→0. Claramente no habrá potencia negativa disipada enRL, así que cuandoRL=RS la potencia máxima,PL|max, se disipa en la carga. La ecuación(???) se convierte
PL|max=12|E|2RL(RS+RS)2=18|E|2RS
Esto se llama la potencia máxima disponible, o simplemente la potencia disponible de la fuente. Entonces las condiciones para la máxima transferencia de potencia sonRL=RS yXL=−XS; es decir, la transferencia máxima de potencia de la fuente a la carga requiere
ZL=Z∗S
También tenga en cuenta que si la impedancia de la fuente en la Figura2.6.4 es resistiva,V=12E a máxima transferencia de potencia.
Una75Ω fuente con una potencia disponible de1 W se termina en un cortocircuito. ¿Cuál es la potencia disipada en la resistencia equivalente Thevenin de la fuente?
Solución
En RF, “75Ωfuente” se refiere a una fuente con una resistencia equivalente a Thevenin de la75Ω cual aquí estáZS. La condición para la máxima transferencia de potencia, y cuando se entrega la potencia completa disponible a la carga, es cuando la impedancia de carga,ZL es el complejo conjugado deZS=75Ω. El circuito para la transferencia máxima de potencia es como se muestra a la derecha.
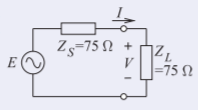
Figura2.6.5
Para resolver el problema debemos determinarE ya que esto no va a cambiar a pesar de que la corriente a travésZSI,, dependerá de la impedancia de carga. La potencia disponible es
PA=12|I|2ℜ(ZS)=12|I|2×75=1 W and so I=√2×1/75=0.1633 A
A partir de esto se puede determinar el voltaje a través de la carga:
V=IZL=0.1633×75=12.25 V and from symmetry E=2V=24.50 V
Ahora se puede determinar la condición con un cortocircuitoZL=0,,. Tenga en cuenta queI yV va a cambiar peroE será fijo.
Considerando el circuito a la derecha, ahora
I=E/(ZS+ZL)=24.50/(75+0)=0.3267 A
El poder disipado enZS es
PS=12I2ℜ(ZS)=0.3267×75=4.002 W
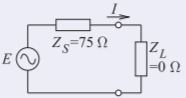
Figura2.6.6
Se pueden hacer algunos comentarios sobre este resultado. Con un cortocircuito la corriente que fluye en el circuito se duplica en comparación con la condición de transferencia de potencia máxima. Dado que la potencia disipada enZS es proporcional al cuadrado de la corriente, la potencia disipada en la resistencia equivalente de Thevenin aumenta en un factor de4 (PSdebería ser exactamente4 W). La fuente de voltaje idealE puede proporcionar energía ilimitada. Sin embargo, no importa cuál sea el valor deZL, la potencia disipada en nuncaZL puede ser más que la potencia disponible.
Una línea de transmisión es accionada por un generador con una potencia máxima disponible de20 dBm y una impedancia equivalente a Thevenin de50Ω. La línea de transmisión tiene una impedancia característica de50Ω.
- ¿Cuál es el voltaje equivalente del generador Thevenin?
- ¿Cuál es la magnitud de la onda de voltaje que viaja hacia adelante en la línea? Supongamos que la línea es infinitamente larga.
- ¿Cuál es la potencia de la onda de voltaje que viaja hacia adelante?
Solución

Figura2.6.7
- La potencia máxima disponible se entrega a la carga cuando se corresponde conjugadamente con la impedancia del generador (ver diagrama de la derecha). EntoncesPLOAD=12V2/R (Ves voltaje pico) (es decir,PLOAD=20 dBm=0.1 W) y
V=√2PLOAD⋅R=√2×0.1×50 Vpeak=3.16 V,EG=2V=6.32 V - Esto es justoV, asíV+=3.16 V.
- P+=20 dBm.
2.6.3 Una sola interfaz
Muchos cálculos de líneas de transmisión se abordan de manera más conveniente utilizando el concepto de potencia máxima disponible. Esto es particularmente así cuando hay múltiples líneas de transmisión. El concepto es que la potencia máxima disponible de una fuente es incidente sobre una carga y si hay un desajuste, se refleja la potencia y se transmite el resto de la potencia. Los circuitos utilizados para ilustrar estos cálculos se muestran en la Figura2.6.8. La potencia disponible de la fuente esPav, la cual es incidente en el plano de referencia que se muestra en la Figura2.6.8 (b) donde se denomina potencia incidentePI. En la potencia del plano de referencia
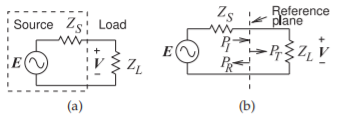
Figura2.6.8: Cálculos usando potencia incidente y reflejada: (a) fuente terminada en una carga; y (b) plano de referencia que ilustra el uso de energía incidente y reflejada en una carga.
se refleja,PR, y se transmite el poder,PT. Usando el coeficiente de reflexión normalizado a la impedancia de la fuente (i.e.,ZS)
PR=|Γ|2PI
donde
Γ=ZS−ZLZS+ZL
y la potencia transmitida es
PT=(1−|Γ|2)PI
La línea de transmisión mostrada en la Figura 2.5.1 (b) consiste en una fuente con impedancia TheveninZ1=40Ω y fuenteE=5 V (pico), conectada a una líneaλ/4 larga de impedancia característicaZ01=40Ω, que a su vez está conectada a una línea infinitamente larga de impedancia característicaZ02=100Ω. Las líneas de transmisión no tienen pérdidas. En la Figura 2.5.1 (b) se muestran dos planos de referencia. En1 el plano de referencia la potencia incidente esPI1 (la potencia máxima disponible de la fuente), la potencia reflejada esPR1, y la potencia transmitida esPT1. PI2(la potencia máxima disponible deZ01)PR2, yPT2 son cantidades similares en el Plano de Referencia2. PI1,PR1,PT1,PI2,PR2,yPT2 son cantidades en estado estacionario.
- ¿Qué esPI1?
- ¿Qué esPT2?
Solución
Dado que la línea infinitamente larga no tiene una onda que viaja hacia atrás, este problema se reduce a un problema de interfaz de línea de transmisión única.
En primer lugar desarrollar algunas expectativas. Esto será un chequeo de cordura durante el problema. PI1yPI2 son potencias máximas disponibles y dado que laZ01 línea (esta es una forma corta de hablar de la línea con una impedancia característicaZ01) es sin pérdidas deberían ser iguales:PI1=PI2. PT1yPT2 son los poderes totales entregados a la derecha de las respectivas interfaces. Nuevamente ya que laZ01 línea es sin pérdidasPT1=PT2, TambiénPT1≤PI1 como la potenciaPR1 se refleja desde la interfaz. De igual maneraPT2≤PI2.
- PI1es la potencia disponible del generador. Dado que la impedancia Thevenin del generador es40Ω,PI1 es la potencia que se entregaría a una carga igualada (la potencia máxima disponible). Un problema equivalente se muestra a la derecha dondeV=12E=2.5 Vpeak. Así
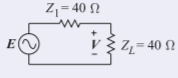
Figura2.6.9
PI1= power in ZL=12(V)21ZL=12(2.5)2140=0.07813 W=78.13 mW
Tenga en cuenta que el12 ocurre porque el voltaje pico se utiliza en los cálculos de RF. - Ahora el problema se vuelve interesante y hay muchas formas de resolverlo. Una de las observaciones clave es que la primera línea de transmisión tiene la misma impedancia característica que la impedancia equivalente Thevenin del generadorZ01=Z1, y así puede ignorarse cuando sea apropiado. Esta observación se utilizará en este ejemplo. Una forma de proceder es calcular directamentePT2, y un segundo enfoque es calcular las potencias incidentes y reflejadas en el plano de referencia2 y luego determinarPT2.
- Primer enfoque: mirando a la izquierda desde el plano de referencia2, el circuito se puede modelar como un circuito equivalente que tiene una resistencia equivalente Thevenin de40Ω y un voltaje equivalente Thevenin que tiene una potencia disponible de78.13 mW. Entonces en el circuito a la derecha,E2 es justoE o5 V.

Figura2.6.10
La carga es100Ω como la segunda línea de transmisión es infinitamente larga. Una pregunta razonable es por qué no loE2 es2.5 V, ya que este sería el voltaje a travésZL=40Ω en la parte (a). Sin embargo,2.5 V es el voltaje de la onda de voltaje de avance en la primera línea de transmisión con impedancia característicaZ01=40Ω. No es el voltaje equivalente Thevenin de la fuente. El voltaje a través de la carga es
V=E210040+100=E100140=3.57 Vpeak
La potencia transmitida en el plano de referencia también2 es la potencia entregada a la carga:
PT2=PL=12(V)21ZL=12(3.57)21100=0.0638 W=63.8 mW
Una comprobación rápida es que esto es menor quePI1, como debería ser. - Segundo enfoque: Esta vezPR2, se calculará la potencia reflejada en el plano2 de referencia. El poder incidente en avión2,PI2, es justoPI1. PI2es la potencia máxima disponible en el plano de referencia2 y no necesariamente la potencia que es incidente allí. En general, para calcularPI2 la fuente equivalente de Thevenin mirando a la izquierda desde el plano de referencia2 necesitaría ser calculada. Sin embargo desde aquíZ01=Z1,PI2=PI1=78.13 mW.
PR2se puede calcular a partir del coeficiente de reflexión de voltaje en el plano de referencia2:
Γ2=ZL−Z01ZL+Z01=100−40100+40=0.429PR2=Γ22P12=0.4292×78 mW=14.36 mW
EntoncesPT2=PI2−PR2=78.13 mW−14.36 mW=63.7 mW, que es la misma que la potencia transmitida calculada en el primer enfoque, lo que permite el error de redondeo. - Un tercer enfoque es calcular la impedancia de entrada mirando a la derecha desde el plano de referencia1, llame a estoZin1. Usando la ecuación del telégrafo sin pérdidas, la Ecuación 2.3.18,Zin1 se calcula para ser16Ω.
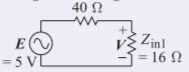
Figura2.6.11
El voltaje a través de la16Ω resistencia es16/(40+16)(5 V)=1.429 V. Entonces el poder disipado enZin1 es
P=12(1.429 V)2116=0.0638 W=63.8 mW
como antes. Toda esta potencia debe transmitirse a la línea infinitamente larga, es decir, lo esPT2, ya que el sistema no tiene pérdidas.
- Primer enfoque: mirando a la izquierda desde el plano de referencia2, el circuito se puede modelar como un circuito equivalente que tiene una resistencia equivalente Thevenin de40Ω y un voltaje equivalente Thevenin que tiene una potencia disponible de78.13 mW. Entonces en el circuito a la derecha,E2 es justoE o5 V.
2.6.4 Diagrama de rebote
Un diagrama de rebote es una representación gráfica de reflexiones en las interfaces entre redes. Una red de microondas se muestra en la Figura2.6.12 donde hay dos planos de referencia en los límites entre diferentes partes de la red. En cada límite hay reflexiones y transmisiones de lo que podrían verse como pequeños paquetes de señales sinusoidales. Mientras que el diagrama de rebote produce un resultado de estado estacionario como la impedancia de entrada, el experimento mental es que pequeños paquetes sinusoidales rebotan alrededor de la red de línea de transmisión. Los diagramas de rebote se utilizan para explorar el impacto de múltiples reflexiones en una red que conducen a la comprensión, y desde eso hasta las decisiones de diseño. Los diagramas de rebote se ilustran mejor a través de un ejemplo.
Coeficientes de reflexión y transmisión en un límite
El análisis del diagrama de rebote requiere que los coeficientes de reflexión y transmisión en un límite sean referenciados a una impedancia común. La figura2.6.13 (a) muestra la interfaz de dos líneas de transmisión de impedancia característicaZ01 yZ02 en un plano de referencia. El problema es determinar el coeficiente de reflexiónΓ, y el coeficiente de transmisiónT, en el límite referenciándolos a la misma impedancia. Aquí se hará referencia a ellosZ01. El coeficiente de reflexión visto desde laZ01 línea a la que se hace referenciaZ01 es
Γ=Z02−Z01Z02+Z01
Ahora el coeficiente de transmisión al que se hace referenciaZ01 es
T=Z01V+2/V+1
dondeZ01V+2 se hace referencia a la onda de voltaje de avance en laZ02 línea (viajando hacia la derecha)Z01. No es el voltaje real que viaja hacia adelante en laZ02 línea. V+1=Z01V+1es la onda de voltaje de desplazamiento en laZ01 línea que es incidente en el límite. Se obtiene utilizando el circuito de la Figura2.6.13 (b). La figura2.6.13 (b) muestra la condición de transferencia de potencia máxima de manera que
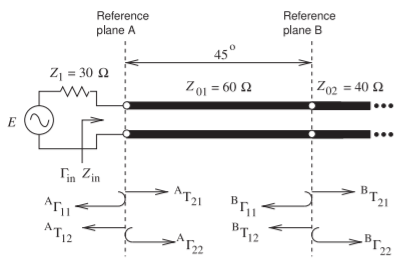
Figura2.6.12: Red de líneas de transmisión con una línea de longitud finita de impedancia característicaZ01 y una línea de transmisión infinitamente larga de impedancia característicaZ02. AΓ1ies lai reflexión discreta de una onda incidente en el lado izquierdo del plano de referenciaA. AT1ies la transmisión en el plano de referenciaA para el mismo evento. AΓ2ies lai reflexión discreta de una onda incidente en el lado derecho del plano de referenciaA.
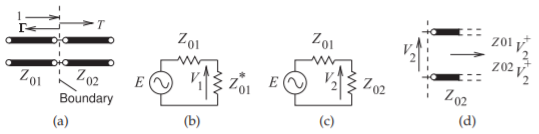
Figura2.6.13: Reflexión (Γ) y transmisión (T) en el límite entre dos líneas de transmisión de impedancia característicaZ01 yZ02.
la onda que viaja hacia adelante en laZ01 línea a la izquierda del límite es
V+1=V1=EZ01Z01+Z∗01=EZ012ℜ(Z01)
(Para impedancias realesV+1=12E.)
El siguiente parámetro a determinar esZ01V+2. Esto comienza determinando el voltaje total,V2, en el límite usando el circuito de la Figura2.6.13 (c):
V2=EZ02Z01+Z02
Ahora considera que laZ02 línea es infinitamente larga, entonces es claro queV2=Z02V+2. Este es el voltaje real que viaja hacia adelante en laZ02 línea. Ahora el problema es cómo cambiar la impedancia de referencia deV+2. Esto se hace señalando que la onda de potencia que viaja hacia adelante es independiente de la impedancia de referencia, por lo tanto, la onda de potencia que viaja hacia adelante en laZ02 línea que viaja a la derecha, lejos del plano de referencia, es
PZ02=12[(Z02V+2)2ℜ(Z02)]=12[(Z01V+2)2ℜ(Z01)]
Por lo tanto, la onda de voltaje que viaja hacia adelante deseada es (desdeZ02V+2=V2)
Z01V+2=√ℜ(Z01)ℜ(Z02)V2=E√ℜ(Z01)ℜ(Z02)(Z02Z01+Z02)
Entonces el coeficiente de transmisión al que se hace referenciaZ01 es
T=Z01V+2V+1=E√ℜ(Z01)ℜ(Z02)(Z02Z01+Z02)(2ℜ(Z01)Z011E)=√ℜ(Z01)ℜ(Z02)[ℜ(Z01)Z01](2Z02Z01+Z02)
Una forma alternativa de determinarT es considerar la conservación de energía en el límite. Entonces
|T|2=1−|Γ|2,that is|T|=±√1−|Γ|2
Esto se puede utilizar siT se espera que sea real, que será siZ01 yZ02 son reales. Se debe tomar el signo positivo. La fórmula más general, Ecuación(2.6.36), se puede utilizar con impedancias complejas.
En el sistema de línea de transmisión de2.6.12 la Figura la longitud eléctrica de laZ01 línea (es decir, la línea con impedancia característicaZ01) es45∘ y laZ02 línea es infinitamente larga. El objetivo aquí es encontrar la impedancia de entrada,Zin. A esto se llegará de dos maneras. La primera técnica utiliza un enfoque de diagrama de rebote y enfatiza la reflexión y transmisión en los planos de interfaz. El segundo enfoque utiliza la ecuación del telégrafo.
- ¿Cuáles son los parámetros de reflexión y transmisión en el plano de referenciaA?
AΓ11es el coeficiente de reflexión de las señales que inciden en el PlanoA de Referencia desde la izquierda. AT21es el coeficiente de transmisión en el plano para las señales de la izquierda. AΓ22yAT12 son los parámetros correspondientes para la dispersión de las señales que vienen de la derecha al plano. Entonces, normalizando aZ1,
AΓ11=Z01−Z1Z01+Z1=0.333
AΓ22=−AΓ11=−0.333
Usando Ecuación(2.6.36),
AT21=√Z1Z01(2Z01Z1+Z01)=√3060(2⋅6030+60)=0.943
Similarmente,AT12=0.943, que se debe a la reciprocidad. Como verificación adicional de cordura (esto solo se puede hacer siZ01 yZ02 son reales)
AT21=√1−AΓ211=0.943AT12=√1−AΓ222=0.943 - ¿Cuáles son los parámetros de dispersiónΓ2 yT2 en el plano de referenciaB?
El referente esZ0, y así el coeficiente de reflexión que va de laZ01 línea a laZ02 línea es
BΓ11=Z02−Z0Z02+Z0
La pregunta ahora es ¿qué impedancia de referencia del sistema utilizar? ¿Debería serZ1,Z01, o inclusoZ02? El problema podría resolverse usando cualquiera de estos, pero el procedimiento más sencillo es usar la misma impedancia de referencia en todas partes, y dado que el objetivo final es calcular el coeficiente de reflexión de entrada global, la elección adecuada esZ0=Z1. Tenga en cuenta, sin embargo, que los niveles de voltaje reales en las líneas no se están calculando (lo que necesitaría ser referenciado a la impedancia característica de las líneas que se están considerando), sino una onda viajera referenciada a una impedancia universal del sistema. Entonces los parámetros de dispersión en el plano de referenciaB referenciado a la impedanciaZ1 son
BΓ11=Z02−Z1Z02+Z1=0.143;BΓ22=−BΓ11=−0.143BT21=√1−AΓ211=0.990;BT12=√1−BΓ222=0.990
La segunda línea de transmisión es infinitamente larga y por lo tanto ninguna señal de la línea incidirá en el planoB de referencia desde la derecha. - ¿A qué se refiere el coeficiente deZ01 transmisión de la línea de transmisiónZ01?
T01es la relación entre la onda que viaja hacia adelante al final de la línea y su valor al inicio de la línea. Usando una impedancia de referencia deZ01, la magnitud del coeficiente de transmisión es uno y gira por la longitud eléctrica de la líneaΘ1=45∘ o0.785 radians:
T01=e−ȷΘ1=exp(−ȷ0.785)=0.707−ȷ0.707 - Dibuja el diagrama de rebote de la red de líneas de transmisión.
El diagrama de rebote se muestra en la Figura2.6.14. - ¿Qué esΓin y por lo tanto qué esZin?
Γines el coeficiente de reflexión de entrada en estado estacionario y se obtiene sumando todas las señales que van a la izquierda desde el plano de referenciaA en la Figura2.6.14. Entonces,
Γin=AΓ11+AT12AT21T201BΓ11+AT12AT21T401BΓ211AΓ22+AT12AT21T601BΓ311AΓ222⋯=AΓ11+AT12AT21T201BΓ11[1+x+x2+⋯]
dondex=T201BΓ11AΓ22. Ahora1/(1−x)=1+x+x2+⋯, y así
Γin=AΓ11+AT12AT21T201BΓ111−T201BΓ11AΓ22=0.333+0.943×0.943×(0.707−ȷ0.707)2×(−0.2)1−(0.707−ȷ0.707)2×(−0.2)×(−0.333)=0.345−ȷ0.177
Γin es la reflexión en el plano de referenciaA y se hace referencia aZ1=30Ω. Entonces la impedancia de entrada es
Zin=Z1(1+Γin1−Γin)=30(1+0.345−ȷ0.17771−0.345+ȷ0.177)=55.39+ȷ23.08Ω - Utilice la ecuación del telégrafo sin pérdidas, Ecuación (2.3.18), para encontrarZin.
La línea infinitamente larga presenta una impedanciaZ02 a la línea60Ω de transmisión. Entonces, la impedancia de entrada que mira dentro de la60Ω línea en el plano de referenciaA es, usando la ecuación del telégrafo sin pérdidas,
Zin=Z01(Z02+ȷZ01tanβℓZ01+ȷZ02tanβℓ)
donde la longitud eléctricaβℓ es45∘ oπ/4 radianes. Tan
Zin=60(40+ȷ60tan(π/4)60+ȷ40tan(π/4))=55.39+ȷ23.08Ω
equivalente al resultado obtenido usando el método del diagrama de rebote (ver Ecuación(???)).
La técnica del diagrama de rebote ayuda en la comprensión física, sin embargo, usar la ecuación del telégrafo es un enfoque menos propenso a errores para resolver problemas de línea de transmisión.
2.6.5 Teoría de las pequeñas reflexiones
Si la discontinuidad en el límite A en la Figura2.6.12 es pequeña (Z1es decir, está cerca deZ01 en lugar de la30Ω/60Ω discontinuidad mostrada) entonces se obtiene una aproximación útil señalando queAΓ11 yAΓ22 son pequeñas yAT21≈AT12≈1 así que en la Ecuación(2.6.48)x≈0. Entonces la ecuación(2.6.48) se convierte, usando la ecuación(???), [6]
Γin≈AΓ11+AT12AT21T201BΓ11≈AΓ11+BΓ11e−2ȷΘ1
Es decir, si la discontinuidad en el plano de referenciaA es pequeña entonces el coeficiente de reflexión de entrada está dominado por la reflexión inicial enA, deZ1 aZ01, y la reflexión inicial enB, deZ01 aZ02, girada el doble de la longitud eléctrica, θ1, de la línea.
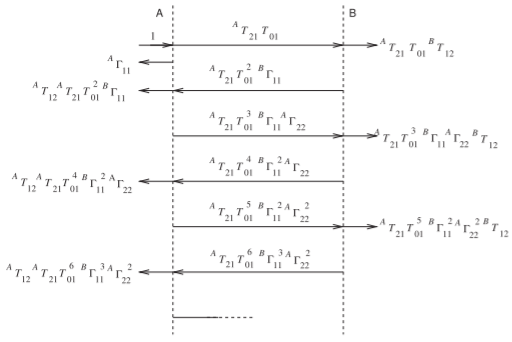
Figura2.6.14: Diagrama de rebote de la red de líneas de transmisión en la Figura2.6.12.
Este ejemplo es similar al Ejemplo2.6.4. Nuevamente, se considera la red de líneas de transmisión de la Figura 2.5.1, pero ahora la impedancia característica de la primera línea de transmisión no es la misma que la impedancia del generador y por lo tanto ya no se puede utilizar la simplificación utilizada en el ejemplo anterior. Ahora el generador tiene una impedanciaZ1=40Ω y fuente TheveninE=5 Vpeak, conectada a una línea larga de un cuarto de longitud de onda de impedancia característicaZ01=30Ω que a su vez está conectada a una línea infinitamente larga de impedancia característicaZ02=100Ω. Las líneas de transmisión no tienen pérdidas. En la Figura 2.5.1 se muestran dos planos de referencia. En1 el plano de referencia la potencia incidente esPI1 (la potencia máxima disponible de la fuente), la potencia reflejada esPR1 y la potencia transmitida esPT1. PI2(la potencia máxima disponible deZ01)PR2, yPT2 son cantidades similares en el plano de referencia2. PI1,PR1,PT1,PI2,PR2,yPT2 son cantidades en estado estacionario.
- ¿Qué esPI1?
- ¿Qué esPT2?
- DeterminarPT1,PI2,PR1, yPR2.
Solución
Una de las primeras cosas a tener en cuenta es que la línea de100Ω transmisión infinitamente larga es indistinguible de una100Ω resistencia, por lo que la forma reducida del problema es como se muestra a continuación.
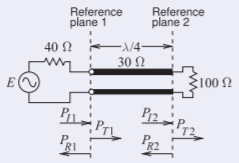
Figura2.6.15
- PI1se calculó en Ejemplo2.6.4 en Ecuación(???):
PI1=78.13 mW
PI1 es la potencia disponible de la fuente y esta es la potencia que se entregaría a una carga que se corresponde conjugadamente con la impedancia de fuente equivalente a Thevenin. - El problema aquí es encontrarPT2. Recordemos que los poderes aquí son cantidades de estado estacionario por lo que no se están considerando múltiples reflexiones de, digamos, un pulso. Dado que el sistema no tiene pérdidas, la potencia entregada por el generador debe ser la potencia entregada a la línea de transmisión infinitamente largaZ02 (es decir,PT2). La ecuación del telégrafo se puede utilizar para calcular la impedancia de entrada,Zin, del sistema de dos líneas de transmisión; es decir, la impedancia de entradaZ01 desde el extremo del generador. Sin embargo, una forma más sencilla de encontrar esta impedancia es darse cuenta de que laZ01 línea es unλ/4 transformador para que
Z01=30Ω=√ZinZ02=√100Zin
y así
Zin=9Ω
El circuito equivalente es como se muestra a continuación, dondeE está el original voltaje del generador de5 V y
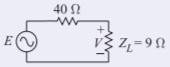
Figura2.6.16
V=940+95=0.9184 V
La potencia entregada por el generador a la9Ω carga es
PT2=12V2/9=0.04686 W=46.86 mW - La potencia transmitida al sistema en el plano de referencia1,PT1, es la misma que la potencia transmitida a la100Ω carga, ya que la primera línea de transmisión es sin pérdidas; es decir,
PT1=PT2=46.86 mW
También
PR1=PI1−PT1=(78.13−46.86) mW=31.27 mW
Los dos cantidades restantes a determinar sonPI2 yPR2. Puede haber una serie de interpretaciones de lo que estos deberían ser, pero una cosa que es cierta es que
PT2=PI2−PR2=46.86 mW
Una interpretación que se seguirá aquí se basa en el circuito equivalente en el plano de referencia2. DejarZout ser la impedancia mirando a la izquierda desde el plano de referencia2. Nuevamente, usando la propiedad de una línea de transmisión larga de un cuarto de longitud de onda,
Z01=30=√Zout×40
y así
Zout=Z201/40=302/40=22.5Ω
El circuito equivalente en el plano de referencia2 es entonces
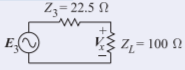
Figura 2.6.17
Ahora determineVx que da como resultado quePT2 se entregue una potencia a la100Ω carga, así
PT2=12V2x/100=0.04686 W
y
Vx=3.06 V
Desde el circuito anterior,
Vx=100100+22.5E3
y así
E3=3.75 V
La potencia disponible de esta fuente se obtiene considerando
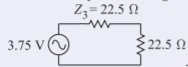
Figura2.6.18
La potencia disponible en el plano de referencia2 es
PI2=12(E3/2)222.5=1.87522×22.5=0.07813 W=78.13 mW
De la Ecuación(???),
PR2=PI2−PT1=(78.13−46.86) mW=31.27 mW
TengaPR2 en cuenta que en Ecuación(???) es lo mismo quePR1 en Ecuación(???), como se esperaba.


