2.7: Modelos de Líneas de Transmisión
( \newcommand{\kernel}{\mathrm{null}\,}\)
Los modelos de líneas de transmisión permiten incorporar líneas en simuladores y relacionadas con circuitos de elementos grumados. En la sección 2.7.1 se presentan modelos utilizados en simuladores de circuitos como Spice. La síntesis de circuitos de microondas a menudo requiere que se realice un diseño de elementos agrupados utilizando una red de línea de transmisión equivalente. La técnica de parámetros ABCD descrita en la Sección 2.7.2 es el principal medio para relacionar estas redes y así sintetizar diseños basados en líneas de transmisión. Este método se utiliza muchas veces en los diseños de esta serie de libros.
2.7.1 Modelos de circuito de líneas de transmisión
Se requieren modelos de circuitos de líneas de transmisión si van a ser utilizados en un simulador de circuitos. La ingeniería de RF y microondas utiliza dos tipos de simuladores. Los simuladores tipo especia utilizan modelos de líneas de transmisión de elementos grumados en los que se replica unRLGC modelo de un segmento corto de línea para la longitud de la línea. Si el plano de tierra se trata como un suelo universal, entonces el modelo de un segmento de longitudΔz es como se muestra en la Figura2.7.1 (a). En este segmentor=RΔz,l=LΔz,g=GΔz, yc=CΔ∆z, dondeR,L,G, yC son los parámetros por unidad de longitud de la línea. Al conectar en cascada los segmentos para obtener la longitud de la línea se obtiene el modelo completo de elementos grumados de la línea, como se muestra en la Figura2.7.1 (b). Este modelo es adecuado si hay un plano de tierra bien definido. De lo contrario, se utiliza la forma más precisa del modelo de segmento que se muestra en la Figura2.7.1 (c). ElL yC de un modelo de línea de transmisión de dos conductores se relacionan con los campos entre los conductores y no con los propios conductores. Por lo que asignarlos a un solo conductor no es exacto. El condensador ya está compartido entre los dos conductores en el modelo original, Figura2.7.1 (a), pero el inductor se asignó a solo uno. El cambio en el modelo de tierra distribuida de la Figura2.7.1 (c) es que la inductancia
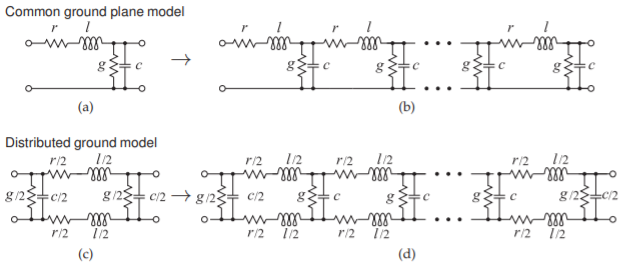
Figura2.7.1: Modelos de líneas de transmisión de elementos agrupados: (a) modelo de un segmento corto (por ejemplo,λ/20 largo); (b) modelo completo de una línea de transmisión; (c) modelo más preciso de un segmento; y (d) modelo preciso completo de una línea de transmisión.
se asigna a cada uno de los conductores.
Uno de los problemas con el modelo de elementos grumados es que no es posible manejarloG correctamente. Gse debe en gran parte a la pérdida de relajación dieléctrica y por lo tanto depende linealmente de la frecuencia. Afortunadamente es muy pequeño para sustratos de RF y microondas y por lo que casi siempre se puede ignorar. Una excepción es un circuito integrado de silicio donde hay una pérdida dieléctrica apreciable. El software de extracción parasitaria se utiliza en el diseño de circuitos integrados de silicio para extraer modelos similares a los de la Figura2.7.1 (d) pero dar cuenta del acoplamiento con otros circuitos. Especialmente en los circuitos digitales, a veces es difícil identificar un plano de tierra (una ruta de retorno de corriente) a excepción de las redes de interconexión críticas como los circuitos de distribución de energía y reloj.
Los filtros de comunicación a menudo se construyen usando varios resonadores de línea de transmisión en cortocircuito que están acoplados entre sí. Considera una línea coaxial que esté cortocircuitada en un extremo. La permitividad que llena la línea coaxial tieneε=20 y el resonador debe diseñarse para resonar a una frecuencia centralf0,, de1850 MHz cuando esλ/4 larga.
- ¿Cuál es la longitud de onda en la línea coaxial con relleno dieléctrico?
- ¿Cuál es la forma del circuito equivalente (en términos de inductores y condensadores) del resonador de un cuarto de longitud de onda si la línea coaxial no tiene pérdidas? Tenga en cuenta que la impedancia de entrada de una línea cortaλ/4 -larga es infinita.
- ¿Cuál es la longitud física del resonador?
Solución
Lo primero que hay que darse cuenta con este ejemplo es que la primera resonancia ocurrirá cuando la longitud del resonador sea de un cuarto de(λ/4) longitud de onda. La resonancia generalmente significa que la impedancia es un circuito abierto o un cortocircuito y hay energía almacenada. Cuando la línea en cortocircuito esλ/4 larga, la impedancia de entrada es un circuito abierto y también se almacena energía.
- λg=λ0/√εr=16.2 cm/√20=3.62 cm. (Aquíλ0=30 cm en1 GHz se utilizó. Por lo tanto, en1850 MHzλ0=(30 cm)/1.85=16.2 cm.)
-
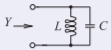
Figura2.7.2
Y=0 en resonancia
Y=YL+YC=1ȷωL+ȷωC=ω−1ȷL+ȷωC - ℓ=(0.0362 m)/4=9.05 mm
Este ejemplo se basa en Ejemplo2.7.1. Los filtros de comunicación RF a menudo se construyen usando varios resonadores de línea de transmisión en cortocircuito que están acoplados entre sí. Considera una línea coaxial que esté cortocircuitada en un extremo. El dieléctrico que llena la línea coaxial tiene unε=20 y el resonador debe diseñarse para resonar a una frecuencia centralf0=1850 MHz.
- ¿Cuál es la longitud de onda en la línea coaxial con relleno dieléctrico?
- ¿Cuál es la forma del circuito equivalente (en términos de inductores y condensadores) del resonador de un cuarto de longitud de onda si la línea coaxial no tiene pérdidas?
- ¿Cuál es la longitud física del resonador?
- Determinar la derivada con respecto a la frecuencia de la admitancia del circuitoLC equivalente desarrollado en (b). Determinar una expresión analítica para la derivada a la frecuencia resonante.
- Si el diámetro del conductor interno de la línea coaxial es2 mm y el diámetro interior del conductor externo es5 mm, ¿cuál es la impedancia característica de la línea coaxial?
- Calcule la admitancia de entrada de la línea coaxial llena de dieléctrico en0.99f0,f0, y1.01f0. Determinar la derivada de frecuencia numérica de la entrada de línea enf0.
- Derivar los valores numéricos del circuito equivalente del resonador en la resonancia.
Solución
Lo primero que hay que darse cuenta es que la primera resonancia ocurrirá cuando la longitud del resonador sea de un cuarto de(λ/4) longitud de onda. La resonancia generalmente significa que la impedancia es un circuito abierto o un cortocircuito y hay energía almacenada. Cuando la línea en cortocircuito esλ/4 larga, la impedancia de entrada será un circuito abierto. Cuando la línea es de longitud cero, la energía no se almacena, por lo que una línea de longitud cero no es un resonador.
- λg=λ0/√εr=16.2 cm/√20=3.62 cm.
-
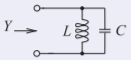
Figura2.7.3
Y=YL+YC=1ȷωL+ȷωC=ω−1ȷL+ȷωC.
Y=0en resonancia. - ℓ=(0.0362 m)/4=9.05 mm.
- De (b),
∂Y∂ω=−ω−2ȷL+ȷC=ȷω2L+ȷC=ȷ(1ω2L+C) - De la Ecuación (2.2.50),Z0=12.28Ω.
- ZL=0Ω,ℓ=(0.0362 m)/4=9.05 mm,β=β0√εr,dondeβ0 β0 es la constante de fase del espacio libre. De las Ecuaciones (2.2.40) y (2.2.41),
β=20.958×f0|GHz×√20=173.4 rad/m
At0.99f0 y usando la Ecuación (2.3.18),Zin=ȷ781.7Ω;Yin=−ȷ0.001279 S.
Enf0,Zin=−ȷ∞Ω;Yin=0 S. En1.01f0,Zin=−ȷ781.7Ω;Yin=ȷ0.001279 S.
Por lo que la derivada de la admitancia de entrada es
∂Y∂ω≈ΔYinΔω=ȷ(0.001279+0.001279)2πf0(1.01−0.99)=ȷ1.101⋅10−11 S⋅s=ȷ1.101⋅10−11 F
Obsérvese la equivalencia de unidad SIS⋅s=F obtenida al examinar la Tabla 2.A.1. - El circuito LC resuena enf0=1.85 GHz cuando1/(ȷω0L)=−ȷω0C;ω0=2πf0. Por lo tanto
LC=ω−20=0.7401×10−20 s2
, ecuando ecuaciones(???) y(???):
1ω20L+C=1.101×10−11 F and so C=1.101×10−11−1ω20L F
Sustituyendo esto en la ecuación(???) (señalando la equivalencia de unidades SIS−1⋅s−1=H:
L(1.101×10−11−1ω20L)=0.7401×10−20 H
1.101×10−11L=1.4802×10−20 HandL=1.345×10−9 H=1.345 nH
De la Ecuación(???),
C=0.7401×10−20/L=5.503×10−12 F=5.503 pF
Entonces el circuito equivalente del resonador es
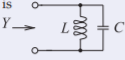
Figura2.7.4
conL=1.345 nH yC=5.503 pF.
Este circuito equivalente es válido para un rango (digamos5\%– 10\%) de frecuencias alrededor1.85\text{ GHz}. La equivalencia de banda ancha se obtuvo aquí al hacer coincidir tanto la admisión como la derivada de la admisión.
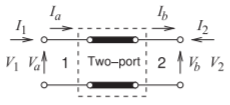
Figura\PageIndex{5}: Red de dos puertos de una línea de transmisión con definiciones de voltaje y corriente en cascada.
2.7.2ABCD (Cadena) Parámetros de una Línea de Transmisión
ABCDLos parámetros, también llamados parámetros de cadena, se utilizan en ingeniería de RF y microondas para equiparar eléctricamente dos estructuras diferentes, como una red de elementos agrupados y una estructura de línea de transmisión. A menudo, el diseño eléctrico se realiza utilizando elementos agrupados y luego estos se convierten en estructuras de líneas de transmisión equivalentes con la equivalencia lograda usandoABCD parámetros.
Figura\PageIndex{5}, muestra los voltajes y corrientes de un puerto de dos puertos en forma de cascada para que las variables de entrada puedan escribirse en términos de las variables de salida:
\label{eq:7}\left[\begin{array}{c}{V_{a}}\\{I_{a}}\end{array}\right]=\left[\begin{array}{cc}{A}&{B} \\ {C}&{D}\end{array}\right]\left[\begin{array}{c}{V_{b}}\\{I_{b}}\end{array}\right]
Tenga en cuenta que la corriente en el puerto 2 está en la dirección opuesta a la definición habitual de la corriente de dos puertos. Entonces, en términos del voltaje y corriente del puerto en el puerto 1, (V_{1}yI_{1}), y el voltaje y corriente del puerto en el puerto 2, (V_{2}yI_{2}),
\label{eq:8}V_{a}=V_{1},\quad I_{a}=I_{1},\quad V_{b}=V_{2},\quad\text{and}\quad I_{b}=-I_{2}
En términos de voltajes de onda viajera, el voltaje total y la corriente en una línea de longitud\ell\gamma, constante de propagación e impedancia característicaZ_{0} = 1/Y_{0} en la posiciónz son
\begin{align}\label{eq:9}V(z)&=V_{0}^{+}e^{-\jmath\gamma(z-\ell)}+V_{0}^{-}e^{\jmath\gamma(z-\ell)} \\ \label{eq:10}I(z)&=Y_{0}V_{0}^{+}e^{-\jmath\gamma(z-\ell)}-Y_{0}V_{0}^{-}e^{\jmath\gamma(z-\ell)}\end{align}
dondeV_{0}^{+} yV_{0}^{-} están los fasores de voltaje de onda viajera enz =\ell, (puerto 2), i.e.
\label{eq:11}V_{0}^{+}=\frac{1}{2}(V_{2}+Z_{0}I_{2})\quad\text{and}\quad V_{0}^{-}=\frac{1}{2}(V_{2}-Z_{0}I_{2})
Sustituyendo estos en Ecuaciones\eqref{eq:9} y\eqref{eq:10},
\begin{align}\label{eq:12}V(z)&=\frac{1}{2}(V_{2}+Z_{0}I_{2})e^{-\jmath\gamma(z-\ell)}+\frac{1}{2}(V_{2}-Z_{0}I_{2})e^{\jmath\gamma(z-\ell)} \\ \label{eq:13}I(z)&=\frac{1}{2}(Y_{0}V_{2}+I_{2})e^{-\jmath\gamma(z-\ell)}-\frac{1}{2}(Y_{0}V_{2}-I_{2})e^{\jmath\gamma(z-\ell)}\end{align}
En el Puerto 1(z = 0)
\begin{align}\label{eq:14}V_{1}=V(0)&=\frac{1}{2}(V_{2}+Z_{0}I_{2})e^{\jmath\gamma\ell}+\frac{1}{2}(V_{2}-Z_{0}I_{2})e^{-\jmath\gamma\ell} \\ \label{eq:15}I_{1}=I(0)&=\frac{1}{2}(Y_{0}V_{2}+I_{2})e^{\jmath\gamma\ell}-\frac{1}{2}(Y_{0}V_{2}-I_{2})e^{-\jmath\gamma\ell}\end{align}
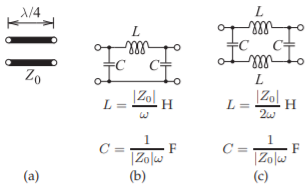
Figura\PageIndex{6}: Circuito equivalente agrupado de una línea larga de un cuarto de longitud de onda de impedancia característicaZ_{0} que es la misma que la de un inversor de impedancia (deZ_{0}\:\Omega): (a) segmento de línea larga de un cuarto de longitud de onda; (b) circuito equivalente a elementos agrupados; y (c) elemento agregado alternativo modelo.
Utilizando las identidades trigonométricas de la Sección 1.A.2 (y señalando queI_{2} = −I_{b}),
\begin{align}\label{eq:16}V_{a}&=V_{1}=\cosh(\gamma\ell)V_{2}-Z_{0}\sinh(\gamma\ell)I_{2}=\cosh(\gamma\ell)V_{b}+Z_{0}\sinh(\gamma\ell)I_{b} \\ \label{eq:17}I_{a}&=I_{1}=Y_{0}\sinh(\gamma\ell)V_{2}-\cosh(\gamma\ell)I_{2}=Y_{0}\sinh(\gamma\ell)V_{b}+\cosh(\gamma\ell)I_{b}\end{align}
Es decir, losABCD parámetros de una línea con pérdida son
\begin{align}A&=\cosh(\gamma\ell) &B&=Z_{0}\sinh(\gamma\ell)\nonumber \\ \label{eq:18}C&=Y_{0}\sinh(\gamma\ell) &D&=\cosh(\gamma\ell)\end{align}
y losABCD parámetros de una línea de transmisión sin pérdidas, donde\gamma=\jmath\beta, son
\begin{align}A&=\cos(\beta\ell) &B&=\jmath Z_{0}\sin(\beta\ell) \nonumber \\ \label{eq:19}C&=\jmath Y_{0}\sin(\beta\ell) &D&=\cos(\beta\ell)\end{align}
Desarrollar el modelo de elementos grumados de una línea de transmisión sin pérdidas de un cuarto de longitud de onda de longitud de onda que tenga impedancia característicaZ_{0}.
Solución
El modelo se desarrolla mediante la equiparación deABCD parámetros. LosABCD parámetros de una línea larga sin pérdidas de longitud de onda de un ecuarter (con\beta\ell = \pi/2) son
\begin{align}\label{eq:20}A&=\cos(\beta\ell)=0 \\ \label{eq:21}B&=\jmath Z_{0}\sin(\beta\ell)=\jmath Z_{0} \\ \label{eq:22}C&=\jmath Y_{0}\sin(\beta\ell)=\jmath /Z_{0} \\ \label{eq:23} D&=\cos(\beta\ell)=0\end{align}
LosABCD parámetros de una red Pi (ver Tabla 2.A.1 de [7]) son
\begin{align}\label{eq:24}A&=1+y_{2}/y_{3} \\ \label{eq:25} B&=1/y_{3} \\ \label{eq:26}C&=y_{1}+y_{2}+y_{1}y_{2}/y_{3} \\ \label{eq:27}D&=1+y_{1}/y_{3}\end{align}
Ecuaciones de equiparación\eqref{eq:21} y\eqref{eq:25},
\label{eq:28}y_{3}=1/(\jmath Z_{0})
y con Ecuaciones\eqref{eq:20}\eqref{eq:23},\eqref{eq:24}, y\eqref{eq:27},
\label{eq:29}y_{1}=y_{2}=-y_{3}=-1/(\jmath Z_{0})
El circuito equivalente agrupado del transformador de cuarto de onda en la Figura\PageIndex{6} (a) se muestra en la Figura\PageIndex{6} (b). En la Figura\PageIndex{6} (c) se muestra un modelo alternativo de elementos grumados. El modelo de elementos grumados de la50\:\Omega línea en400\text{ MHz} se muestra en la Figura\PageIndex{6} (b) conL = 19.89\text{ nH} yC = 7.968\text{ pF}. Este es un modelo más simple y preciso de una línea\lambda/4 larga que un modelo con múltiples segmentos de línea corta como en la Figura\PageIndex{1}.


