2.8: Líneas de transmisión de dos conductores

Casi todas las líneas de transmisión de dos conductores admiten campos EM a frecuencias de hasta CC. Como resultado, tales líneas generalmente se pueden caracterizar en CC y las propiedades de las líneas serán esencialmente las mismas en frecuencias de RF. A continuación se presentan las impedancias características de los tipos más comunes de líneas de dos conductores. Para todas estas líneas la constante de fase es la misma que sería en el medio sin conductores (i.e.,$\beta =\omega\sqrt{\mu\varepsilon}$). Las impedancias características son modificaciones de la impedancia de onda de espacio libre$\eta_{0} =\sqrt{\mu_{0}/\varepsilon_{0}} = 120\pi\:\Omega = 376.73\:\Omega$. Las propiedades de muchas otras líneas de transmisión se dan en [8].

---

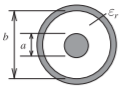
Figura$\PageIndex{1}$: Línea coaxial

$$\label{eq:1}Z_{0}=\frac{\eta_{0}}{2\pi}\sqrt{\frac{\mu_{r}}{\varepsilon_{r}}}\ln\left(\frac{b}{a}\right)=60\sqrt{\frac{\mu_{r}}{\varepsilon_{r}}}\ln\left(\frac{b}{a}\right)$$

Exacto. Ver derivación en la Sección 2.9.

---

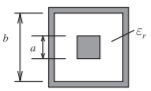
Figura$\PageIndex{2}$: Línea coaxial cuadrada

$$\label{eq:2}Z_{0}\approx\eta_{0}\sqrt{\frac{\mu_{r}}{\varepsilon_{r}}}\left[4\left(\frac{2a}{b-a}+0.558\right)\right]^{-1}$$

Precisión típica:$<1\%$ para$b/a\leq 4$. Referencia [9].

---

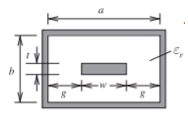
Figura$\PageIndex{3}$: Línea coaxial rectangular

$$\label{eq:3}Z_{0}=\frac{\eta_{0}}{4}\sqrt{\frac{\mu_{r}}{\varepsilon_{r}}}\left(\frac{\omega}{b-t}+\frac{1}{\pi}\left\{\frac{b}{b-t}\ln\left(\frac{2b-t}{t}\right)+\ln\left[\frac{t(2b-t)}{(b-t)^{2}}\right]\right\}\frac{\ln[1+\coth(\pi g/b)]}{\ln 2}\right)^{-1}$$

Precisión típica:$1\%$. Referencias [10, 11, 12].

---

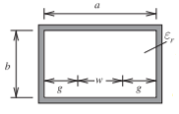
Figura$\PageIndex{4}$: Línea coaxial rectangular, tira delgada$t\to 0$

$$\label{eq:4}Z_{0}=\frac{\eta_{0}}{4}\sqrt{\frac{\mu_{r}}{\varepsilon_{r}}}\left\{\frac{\omega}{b}+\frac{2}{\pi}\ln\left[1+\coth\left(\frac{\pi g}{b}\right)\right]\right\}^{-1}$$

Precisión típica:$1\%$. Referencia [10].

---

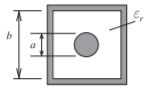
Figura$\PageIndex{5}$: Coaxial cuadrado con conductor interno circular

$$\label{eq:5}Z_{0}=\frac{\eta_{0}}{2\pi}\sqrt{\frac{\mu_{r}}{\varepsilon_{r}}}\ln\left(\frac{1.0787b}{a}\right)$$

Precisión típica:$1.5\%$. Referencias [8, 13, 14, 15].

---

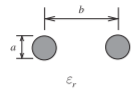
Figura$\PageIndex{6}$: Alambres paralelos

$$\label{eq:6}Z_{0}=\frac{\eta_{0}}{\pi}\sqrt{\frac{\mu_{r}}{\varepsilon_{r}}}\text{arccosh}\left(\frac{b}{a}\right)$$

Precisión típica:$1\%$. Referencias [16, 17].

---

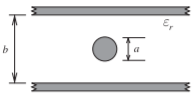
Figura$\PageIndex{7}$: Línea de losa

$$\label{eq:7}Z_{0}=15\sqrt{\frac{\mu_{r}}{\varepsilon_{r}}}\ln\left[1+1.314g+\sqrt{(1.314g)^{2}+2g}\right]\quad\text{where }g=(b/a)^{4}-1$$

Precisión típica:$0.5\%$. Referencia [18].

---

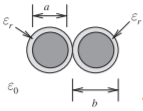
Figura$\PageIndex{8}$: Par trenzado con$T$ giros por unidad de longitud

$$\begin{align}\label{eq:8}Z_{0}&=\frac{\eta_{0}}{\pi}\sqrt{\frac{\mu_{r}}{\varepsilon_{e}}}\text{arccosh}\left(\frac{b}{a}\right) \\ \varepsilon_{e}&=1+q(\varepsilon_{r}-1),\: q=0.25+0.0004\Theta^{2} \\ T&=\frac{\tan\Theta}{\pi D}\text{ so }\Theta -\arctan(T\pi D)\nonumber\end{align} \nonumber$$

Precisión típica:$1\%$. Referencia [19].

---

Características de las líneas de transmisión de dos conductores.