2.12: Ejercicios

Última actualización
Guardar como PDF

Page ID: 82142

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Una línea coaxial se cortocircuita en un extremo y se llena con un dieléctrico con una permitividad relativa de\(64\). [Ejemplo de Parallels 2.1.1]
1. ¿Cuál es la longitud de onda del espacio libre\(18\text{ GHz}\)?
2. ¿Cuál es la longitud de onda en la línea coaxial llena de dieléctrico\(18\text{ GHz}\)?
3. La primera resonancia del resonador coaxial está en\(18\text{ GHz}\). ¿Cuál es la longitud física del resonador?
Una línea de transmisión tiene los siguientes\(RLGC\) parámetros:\(R = 100\:\Omega\text{/m},\: L = 85\text{ nH/m},\: G = 1\text{ S/m},\) y\(C = 150\text{ pF/m}\). Considere una onda viajera en la línea de transmisión con una frecuencia de\(1\text{ GHz}\). [Ejemplo de Parallels 2.2.2]
1. ¿Cuál es la constante de atenuación?
2. ¿Cuál es la constante de fase?
3. ¿Cuál es la velocidad de fase?
4. ¿Cuál es la impedancia característica de la línea?
5. ¿Cuál es la velocidad del grupo?
Una línea de transmisión tiene los parámetros de longitud por unidad\(L = 85\text{ nH/m},\: G = 1\text{ S/m},\) y\(C = 150\text{ pF/m}\). Utilice una frecuencia de\(1\text{ GHz}\). [Ejemplo de Parallels 2.2.2]
1. ¿Cuál es la velocidad de fase si\(R = 0\:\Omega\text{/m}\)?
2. ¿Cuál es la velocidad del grupo si\(R = 0\:\Omega\text{/m}\)?
3. Si\(R = 10\text{ k}\Omega\text{/m}\) ¿cuál es la velocidad de fase?
4. Si\(R = 10\text{ k}\Omega\text{/m}\) ¿cuál es la velocidad del grupo?
Una línea es\(10\text{ cm}\) larga y a la frecuencia de operación la constante de fase\(\beta\) es\(40\text{ rad/m}\). ¿Cuál es la longitud eléctrica de la línea? [Ejemplo de Parallels 2.1.2]
Una línea de transmisión sin pérdidas llena de dieléctrico que lleva una\(1\text{ GHz}\) señal tiene los parámetros\(L = 80\text{ nH/m}\) y\(C = 200\text{ pF/m}\). Cuando el dieléctrico es reemplazado por aire, la capacitancia de la línea es\(C_{\text{air}} = 50\text{ pF/m}\). ¿Cuál es la permitividad relativa del dieléctrico?
Una línea de transmisión coaxial está llena de material dieléctrico con pérdidas con una permitividad relativa de\(5 −\jmath 0.2\). Si la línea está llena de aire tendría una impedancia característica de\(100\:\Omega\). ¿Cuál es la impedancia de entrada de la línea si es\(1\text{ km}\) larga? Utilizar aproximaciones razonables. [Pista: ¿Importa la terminación?]
Una línea de transmisión tiene los parámetros por unidad de longitud\(R = 2\Omega\text{/cm},\: L=100\text{ nH/m},\: G = 1\text{ mS/m},\: C = 200\text{ pF/m}\).
1. ¿Cuál es la constante de propagación de la línea\(5\text{ GHz}\)?
2. ¿Cuál es la impedancia característica de la línea\(5\text{ GHz}\)?
3. Trazar la magnitud de la impedancia característica versus frecuencia de\(100\text{ MHz}\) a\(10\text{ GHz}\).
Una línea es\(20\text{ cm}\) larga y en\(1\text{ GHz}\) la constante de fase\(\beta\) es\(20\text{ rad/m}\). ¿Cuál es la longitud eléctrica de la línea en grados?
¿Cuál es la longitud eléctrica de una línea que tiene un cuarto de longitud de onda?
1. en grados?
2. en radianes?
Una línea de transmisión sin pérdidas tiene una inductancia de\(8\text{ nH/cm}\) y una capacitancia de\(40\text{ pF/cm}\).
1. ¿Cuál es la impedancia característica de la línea?
2. ¿Cuál es la velocidad de fase en la línea\(1\text{ GHz}\)?
Una línea aérea\(50\:\Omega\) coaxial es una línea coaxial sin dieléctrico (es decir, está llena de aire) y con discos dieléctricos delgados que soportan el conductor interno tienen un efecto despreciable. Si el aire es reemplazado por un dieléctrico que tiene una permitividad relativa de\(20\), ¿cuál es la impedancia característica de la línea llena de dieléctrico?
Una línea de transmisión tiene una atenuación de\(2\text{ dB/m}\) y una constante de fase de\(25\text{ radians/m}\) at\(2\text{ GHz}\). [Ejemplo de Parallels 2.2.3]
1. ¿Cuál es la constante de propagación compleja de la línea de transmisión?
2. Si la capacitancia de la línea es\(50\text{ pF}\cdot\text{m}^{−1}\) y\(G = 0\), ¿cuál es la impedancia característica de la línea?
Una línea de transmisión de microcinta de muy baja pérdida tiene los siguientes parámetros por unidad de longitud:\(R = 2\:\Omega\text{/m},\: L = 80\text{ nH/m},\: C = 200\text{ pF/m},\) y\(G = 1\:\mu\text{S/m}\).
1. ¿Cuál es la impedancia característica de la línea si se ignora la pérdida?
2. ¿Cuál es la constante de atenuación debido a la pérdida del conductor?
3. ¿Cuál es la constante de atenuación debida a la pérdida dieléctrica?
Una línea de transmisión sin pérdidas que transporta una\(1\text{ GHz}\) señal tiene los siguientes parámetros por unidad de longitud:\(L = 80\text{ nH/m},\: C = 200\text{ pF/m}\).
1. ¿Cuál es la constante de atenuación?
2. ¿Cuál es la constante de fase?
3. ¿Cuál es la velocidad de fase?
4. ¿Cuál es su impedancia característica?
Una línea de transmisión tiene una impedancia característica\(Z_{0}\) y se termina en una carga con un coeficiente de reflexión de\(0.8\angle 45^{\circ}\). Una onda de voltaje que viaja hacia adelante en la línea tiene una potencia de\(1\text{ dBm}\).
1. ¿Cuánta potencia se refleja en la carga?
2. ¿Cuál es la potencia entregada a la carga?
Una línea de transmisión tiene una atenuación de\(0.2\text{ dB/cm}\) y una constante de fase de\(50\text{ radians/m}\) at\(1\text{ GHz}\).
1. ¿Cuál es la constante de propagación compleja de la línea de transmisión?
2. Si la capacitancia de la línea es\(100\text{ pF/m}\) y\(G = 0\), ¿cuál es la impedancia característica compleja de la línea?
3. Si la línea es accionada por una fuente modelada como una tensión ideal y una impedancia en serie, ¿cuál es la impedancia de la fuente para una transferencia máxima de potencia a la línea de transmisión?
4. Si\(1\text{ W}\) el generador entrega (es decir, en la onda que viaja hacia adelante) a la línea de transmisión, ¿cuál es la potencia en la onda que viaja hacia adelante en la línea\(2\text{ m}\) desde el generador?
La línea de transmisión mostrada en la Figura 2.5.1 consiste en una fuente con impedancia Thevenin\(Z_{1} = 40\:\Omega\) y fuente\(E = 5\text{ V}\) (pico) conectada a una línea\(\lambda/4\) larga de impedancia característica\(Z_{01} = 50\:\Omega\), que a su vez está conectada a una línea infinitamente larga de impedancia característica\(Z_{02} = 100\:\Omega\). Las líneas de transmisión no tienen pérdidas. En la Figura 2.5.1 se muestran dos planos de referencia. En\(\mathsf{1}\) el plano de referencia la potencia incidente es\(P_{I1}\), la potencia reflejada es\(P_{R1}\), y la potencia transmitida es\(P_{T1}\). \(P_{I2},\: P_{R2},\)y\((P_{T2})\) son cantidades similares en el plano de referencia\(\mathsf{2}\). [Ejemplos de Parallels 2.6.4 y 2.6.6]
1. ¿Qué es\(P_{I1}\)?
2. ¿Qué es\(P_{T2}\)?
Una línea de\(75\:\Omega\) transmisión sin pérdidas,\(10\text{ cm}\) larga, es impulsada por un\(1\text{ GHz}\) generador con una impedancia equivalente a Thevenin de\(50\:\Omega\). La potencia máxima que se puede entregar a una carga conectada al generador es\(2\text{ W}\). La línea se termina en una carga que tiene un coeficiente de reflexión complejo (referido\(50\:\Omega\)) de\(0.65 +\jmath 0.65\). La permitividad relativa efectiva,\(\varepsilon_{e}\), de la línea de transmisión no magnética es\(2.0\).
1. Calcule la onda de voltaje de avance (en el extremo del generador de la línea de transmisión). Ignorar los reflejos de la carga al final de la\(75\:\Omega\) línea.
2. ¿Cuál es la impedancia de carga?
3. ¿Cuál es la longitud de onda de la onda de voltaje de desplazamiento directo?
4. ¿Qué es el VSWR en la línea?
5. ¿Cuál es la constante de propagación de la línea?
6. ¿Cuál es el coeficiente de reflexión de entrada (en el extremo del generador) de la línea?
7. ¿Cuál es la potencia entregada a la carga?
La primera resonancia de una línea de transmisión no magnética de circuito abierto sin pérdidas está en\(30\text{ GHz}\). La permitividad relativa efectiva de la línea es\(12\).
1. ¿Cuál es la impedancia de entrada del resonador?
2. Dibuja su circuito LC equivalente.
3. ¿Cuál es su longitud eléctrica?
4. ¿Cuál es su longitud física?
Una línea de transmisión de circuito abierto se utiliza como resonador. ¿Cuál es la longitud eléctrica de la línea en su primera resonancia?
La segunda resonancia de una línea de transmisión de circuito abierto se utiliza como resonador.
1. ¿Cuál es su impedancia de entrada?
2. ¿Cuál es su longitud eléctrica?
Una línea de transmisión sin pérdidas es accionada por un\(1\text{ GHz}\) generador que tiene una impedancia equivalente Thevenin de\(50\:\Omega\). La línea de transmisión es sin pérdidas, tiene una impedancia característica de\(75\:\Omega\), y es infinitamente larga. La potencia máxima que se puede entregar a una carga conectada al generador es\(2\text{ W}\).
1. ¿Cuál es el voltaje total (fasor) en la entrada a la línea de transmisión?
2. ¿Cuál es la magnitud de la onda de voltaje de avance en el lado del generador de la línea?
3. ¿Cuál es la magnitud de la onda de corriente que viaja hacia adelante en el lado del generador de la línea?
Una línea de transmisión termina en un cortocircuito. ¿Cuál es la relación entre las ondas de voltaje que viajan hacia adelante y hacia atrás en la terminación? [Ejemplo de Parallels 2.3.1]
Una línea de\(50\:\Omega\) transmisión termina en una\(40\:\Omega\) carga. ¿Cuál es la relación entre las ondas de voltaje hacia adelante y hacia atrás en la terminación? [Ejemplo de Parallels 2.3.1]
Una línea de\(50\:\Omega\) transmisión termina en un circuito abierto. ¿Cuál es la relación entre las ondas de voltaje de avance a las que viajan hacia atrás en la terminación? [Ejemplo de Parallels 2.3.1]
El resonador de abajo está construido a partir de una\(3.0\text{ cm}\) longitud de línea coaxial\(100\:\Omega\) llena de aire, cortocircuitada en un extremo y terminada con un condensador en el otro extremo.

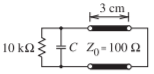
Figura\(\PageIndex{1}\)

¿Cuál es la frecuencia resonante más baja de este circuito sin el condensador (ignore la\(10\text{ k}\Omega\) resistencia)?
¿Cuál es el valor del condensador para lograr la resonancia de orden más bajo en\(6.0\text{ GHz}\) (ignorar la\(10\text{ k}\Omega\) resistencia)?
Supongamos que la pérdida se introduce colocando una\(10\text{ k}\Omega\) resistencia en paralelo con el condensador. ¿Cuál es el\(Q\) del circuito?
Aproximadamente ¿cuál es el ancho de banda del circuito?

Una línea\(50\:\Omega\) de transmisión termina en una carga que da como resultado un coeficiente de reflexión de\(0.5+\jmath 0.5\).
1. ¿Cuál es la impedancia de carga?
2. ¿Qué hay\(\text{VSWR}\) en la línea?
3. ¿Cuál es la impedancia de entrada si la línea tiene media longitud de onda?
Los filtros de comunicación a menudo se construyen usando varios resonadores de línea de transmisión en cortocircuito que están acoplados por elementos pasivos como condensadores. Considera una línea coaxial que esté cortocircuitada en un extremo. El relleno dieléctrico de la línea coaxial tiene una permitividad relativa de\(64\) y el resonador debe diseñarse para resonar a una frecuencia central,\(f_{0}\), de\(800\text{ MHz}\). [Ejemplo de Parallels 2.7.2]
1. ¿Cuál es la longitud de onda en la línea coaxial con relleno dieléctrico?
2. ¿Cuál es la forma del circuito equivalente (en términos de inductores y condensadores) del resonador de un cuarto de longitud de onda si la línea coaxial no tiene pérdidas?
3. ¿Cuál es la longitud del resonador?
4. Si el diámetro del conductor interno de la línea coaxial es\(2\text{ mm}\) y el diámetro interior del conductor externo es\(5\text{ mm}\), ¿cuál es la impedancia característica de la línea coaxial?
5. Calcule la admitancia de entrada de la línea coaxial llena de dieléctrico en\(0.99f_{0},\: f_{0},\) y\(1.01f_{0}\). Determinar la derivada numérica de la entrada de línea en\(f_{0}\).
6. Derivar los valores del circuito equivalente del resonador a la frecuencia resonante y derivar el circuito equivalente del resonador. Pista: Coincidir la expresión derivada derivada en (e) con la derivada real derivada en el Ejemplo 2.7.2.
Desarrollar una fórmula analítica que relacione un coeficiente de reflexión\((\Gamma_{1})\) en un sistema\((Z_{01})\) de referencia con un coeficiente de reflexión\((\Gamma_{2})\) en otro sistema de referencia\((Z_{02})\).
Una línea tiene una impedancia característica\(Z_{0}\) y se termina en una carga con un coeficiente de reflexión de\(0.8\). Una onda de voltaje que viaja hacia adelante en la línea tiene una potencia de\(1\text{ W}\).
1. ¿Cuánta potencia se refleja en la carga?
2. ¿Cuál es la potencia entregada a la carga?
Una carga consiste en una conexión de derivación de un condensador de\(10\text{ pF}\) y una resistencia de\(25\:\Omega\). La carga termina una línea de\(50\:\Omega\) transmisión sin pérdidas. La frecuencia de operación es\(1\text{ GHz}\). [Ejemplo de Parallels 2.3.2]
1. ¿Cuál es la impedancia de la carga?
2. ¿Cuál es la impedancia normalizada de la carga (normalizada a la impedancia característica de la línea)?
3. ¿Cuál es el coeficiente de reflexión de la carga?
4. ¿Cuál es el coeficiente de reflexión actual de la carga?
5. ¿Cuál es la relación de onda estacionaria (SWR)?
6. ¿Cuál es la relación actual de onda estacionaria (ISWR)?
Una línea de transmisión\(50\:\Omega\) llena de aire está conectada entre una\(40\text{ GHz}\) fuente con una impedancia equivalente Thevenin de\(50\:\Omega\) y una carga. El SWR en la línea es\(3.5\).
1. ¿Cuál es la magnitud del coeficiente de reflexión,\(\Gamma_{L}\), a la carga?
2. ¿Cuál es la constante de fase\(\beta\),, de la línea?
3. Si el primer mínimo de la tensión de onda estacionaria en la línea de transmisión es\(2\text{ mm}\) de la carga, determine la distancia eléctrica (en grados) del mínimo de SWR desde la carga.
4. Determinar el ángulo de\(\Gamma_{L}\) a la carga.
5. ¿Qué hay\(\Gamma_{L}\) en forma de fase de magnitud?
6. ¿Qué es\(\Gamma_{L}\) en forma rectangular?
7. Determinar la impedancia de carga,\(Z_{L}\).
Una carga consiste en una resistencia de\(100\:\Omega\) en paralelo con un\(5\text{ pF}\) condensador con una señal eléctrica en\(2\text{ GHz}\).
1. ¿Cuál es la impedancia de carga?
2. ¿Cuál es el coeficiente de reflexión en un sistema de\(50\:\Omega\) referencia?
3. ¿Qué es el SWR en una línea\(50\:\Omega\) de transmisión conectada a la carga?
Un amplificador está conectado a una carga por una línea de transmisión que coincide con el amplificador. Si el SWR en la línea es\(1.5\), ¿qué porcentaje de la potencia del amplificador disponible es absorbido por la carga?
Un amplificador de salida puede tolerar una discordancia con un SWR máximo de\(2.0\). El amplificador se caracteriza por un circuito equivalente a Thevenin con una impedancia de\(50\:\Omega\) y está conectado directamente a una antena caracterizada por una resistencia de carga\(R_{L}\). Determinar los límites de tolerancia\(R_{L}\) para que el amplificador no se autodestruya.
Una carga tiene un coeficiente de reflexión de\(0.5\) cuando se refiere\(50\:\Omega\). La carga se coloca al final de una línea\(100\:\Omega\) de transmisión.
1. ¿Cuál es la compleja relación entre la onda que viaja hacia adelante y la onda que viaja hacia atrás en la\(100\:\Omega\) línea en el extremo de carga de la línea?
2. ¿Qué es el VSWR en la\(100\:\Omega\) línea?
Una carga tiene un coeficiente de reflexión de\(0.5\) cuando se refiere\(50\:\Omega\). La carga se encuentra al final de una línea con una impedancia\(50\:\Omega\) característica.
1. Si la línea tiene una longitud eléctrica de\(45^{\circ}\), ¿cuál es el coeficiente de reflexión calculado en la entrada de la línea?
2. ¿Qué es el VSWR en la\(50\:\Omega\) línea?
Una\(100\:\Omega\) resistencia en paralelo con un\(5\text{ pF}\) condensador termina una línea\(100\:\Omega\) de transmisión. Calcule el SWR en la línea en\(2\text{ GHz}\).
Una línea de\(50\:\Omega\) transmisión sin pérdidas tiene un\(50\:\Omega\) generador en un extremo y termina en\(100\:\Omega\). ¿Qué es el VSWR en la línea?
Una\(75\:\Omega\) línea sin pérdidas es accionada por un\(75\:\Omega\) generador. La línea se termina en una carga que con un coeficiente de reflexión (referido\(50\:\Omega\)) de\(0.5 + \jmath 0.5\). ¿Qué es el VSWR en la línea?
Una carga con un\(20\text{ pF}\) condensador en paralelo con una\(50\:\Omega\) resistencia termina una\(25\:\Omega\) línea. La frecuencia de operación es\(5\text{ GHz}\). [Ejemplo de Parallels 2.3.3]
1. ¿Qué es el VSWR?
2. ¿Qué es ISWR?
Una carga\(Z_{L} = 55−\jmath 55\:\Omega\) y la impedancia de referencia del sistema,\(Z_{0}\), es\(50\:\Omega\). [Ejemplo de Parallels 2.3.4]
1. ¿Cuál es el coeficiente de reflexión de carga\(\Gamma_{L}\)?
2. ¿Cuál es el coeficiente de reflexión actual?
3. ¿Qué es el VSWR en la línea?
4. ¿Qué es el ISWR en la línea?
5. Ahora considere una fuente conectada directamente a la carga. La fuente tiene una impedancia equivalente a Thevenin\(Z_{G} = 60\:\Omega\) y una potencia disponible de\(1\text{ W}\). \(\Gamma_{L}\)Úselo para encontrar la energía entregada a\(Z_{L}\).
6. ¿Cuál es la potencia total absorbida por\(Z_{G}\)?
Una línea ranurada, como se muestra en la Figura 2.3.7 (c), se utiliza para caracterizar una\(50\:\Omega\) línea terminada en una carga\(Z_{L}\). \(V_{\text{max}} = 1\text{ V}\)y\(V_{\text{min}} = 0.1\text{ V}\), y el primer mínimo es\(5\text{ cm}\) de la carga. La longitud de onda guía es\(30\text{ cm}\). ¿Qué es\(Z_{L}\)? [Ejemplo de Parallels 2.3.5]
Una línea coaxial cortocircuitada se utiliza como resonador. Se determina que la primera resonancia es una resonancia paralela y está en\(1\text{ GHz}\).
1. Dibuje el circuito equivalente de elementos grumados del resonador.
2. ¿Cuál es la longitud eléctrica del resonador?
3. ¿Cuál es la impedancia que mira en la línea en resonancia?
4. Si el resonador es\(\lambda/4\) más largo, ¿cuál es la impedancia del resonador ahora?
Una carga de\(100\:\Omega\) debe ser emparejada a una línea de transmisión con una impedancia característica de\(50\:\Omega\). Use un transformador de cuarto de onda. ¿Cuál es la impedancia característica del transformador de cuarto de onda?
Determinar la impedancia característica de un transformador de cuarto de onda utilizado para hacer coincidir una carga de\(50\:\Omega\) a un generador con una impedancia equivalente a Thevenin de\(75\:\Omega\).
Una línea de transmisión debe insertarse entre una\(5\:\Omega\) línea y una\(50\:\Omega\) carga para que haya una transferencia máxima de potencia a la\(50\:\Omega\) carga en\(20\text{ GHz}\).
1. ¿Cuál es la longitud de la línea insertada en términos de longitudes de onda\(20\text{ GHz}\)?
2. ¿Cuál es la impedancia característica de la línea\(20\text{ GHz}\)?
El resonador de abajo está construido a partir de una\(3.0\text{ cm}\) longitud de línea coaxial\(100\:\Omega\) llena de aire cortocircuitada en un extremo y terminada con un condensador en el otro extremo:

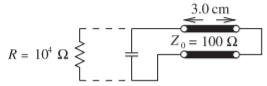
Figura\(\PageIndex{2}\)

¿Cuál es la frecuencia resonante más baja de este circuito sin el condensador (ignore la resistencia)?
¿Cuál es el valor del condensador requerido para lograr la resonancia\(6.0\text{ GHz}\)?
Supongamos que la pérdida se introduce colocando una\(10\text{ k}\Omega\) resistencia en paralelo con el condensador. ¿Cuál es el\(Q\) del circuito?
¿Cuál es el ancho de banda del circuito?

Una línea de transmisión coaxial está llena de material con pérdidas con una permitividad relativa de\(5 −\jmath 0.2\). Si la línea está llena de aire tendría una impedancia característica de\(100\:\Omega\).
1. ¿Cuál es la impedancia característica de la línea llena de dieléctrico?
2. ¿Cuál es la constante de propagación\(500\text{ MHz}\)?
3. ¿Cuál es la impedancia de entrada de la línea si tiene una longitud eléctrica de\(280^{\circ}\) y está terminada en una\(35\:\Omega\) resistencia?
Una línea coaxial se rellena con un material muy ligeramente perdido con una permitividad relativa de\(5\). La línea tendría una impedancia característica de\(100\:\Omega\) si estuviera llena de aire.
1. ¿Cuál es la impedancia característica de la línea llena de dieléctrico?
2. ¿Cuál es la constante de propagación\(500\text{ MHz}\)? Utilice el hecho de que la velocidad de una onda EM en una línea llena de aire sin pérdidas es la misma que la de la propagación del espacio libre en el aire.
3. ¿Cuál es la impedancia de entrada de la línea si tiene una longitud eléctrica de\(90^{\circ}\) y está terminada en una\(35\:\Omega\) resistencia?
4. ¿Cuál es la impedancia de entrada de la línea si tiene una longitud eléctrica de\(180^{\circ}\) y termina en una impedancia\(\jmath 35\:\Omega\)?
5. ¿Cuál es la impedancia de entrada de la línea si es\(1\text{ km}\) larga? Utilizar aproximaciones razonables.
Una línea de transmisión con pérdida con una impedancia característica de\(60 −\jmath 2\:\Omega\) es accionada por un generador con una impedancia equivalente a Thevenin\(Z_{g}\). Si la línea es infinitamente larga, ¿qué es\(Z_{g}\) para la transferencia máxima de potencia del generador a la línea?
Una línea\(25\:\Omega\) de transmisión es accionada por un generador con una potencia disponible de\(23\text{ dBm}\) y una impedancia equivalente a Thevenin de\(60\:\Omega\). [Ejemplo de Parallels 2.6.3]
1. ¿Cuál es el voltaje equivalente del generador Thevenin?
2. ¿Cuál es la magnitud de la onda de voltaje de avance en la línea? Supongamos que la línea es infinitamente larga.
3. ¿Cuál es la potencia de la onda de voltaje que viaja hacia adelante?
Una línea coaxial de circuito abierto se utiliza como resonador. La primera resonancia es una resonancia en serie en\(2\text{ GHz}\). [Ejemplo de Parallels 2.5.1]
1. Dibuje el circuito equivalente de elementos grumados del resonador.
2. ¿Cuál es la longitud eléctrica del resonador?
3. ¿Cuál es la impedancia que mira en la línea en resonancia?
4. Si el resonador es\(3\lambda_{g}/4\) más largo, ¿cuál es la impedancia de entrada del resonador?
La ola que viaja hacia adelante en una\(60\:\Omega\) línea tiene una potencia de\(2\text{ mW}\). La línea se termina en una resistencia de\(50\:\Omega\). Cuánta energía se entrega a la\(50\:\Omega\) carga.
La ola que viaja hacia adelante en una\(40\:\Omega\) línea tiene una potencia de\(2\text{ mW}\). La línea se termina en una resistencia de\(60\:\Omega\). ¿Cuánta potencia hay en la ola que viaja hacia atrás?
La ola que viaja hacia adelante en una\(60\:\Omega\) línea tiene una potencia de\(2\text{ mW}\). La línea se termina en una resistencia de\(50\:\Omega\). Dibuje el circuito equivalente a elementos grumados en la interfaz de la línea y la carga. [Ejemplo de Parallels 2.6.1]
Una fuente está conectada a una carga por una línea de transmisión larga de una longitud de onda que tiene una pérdida de\(1.5\text{ dB}\). El coeficiente de reflexión de origen (referido a la línea de transmisión) es\(0.2\) y el coeficiente de reflexión de carga es\(0.5\).
1. ¿Cuál es el coeficiente de transmisión?
2. Dibuja el diagrama de rebote usando los coeficientes de transmisión y reflexión. Determinar el coeficiente de transmisión efectivo general desde la fuente hasta la carga. Calcule la potencia entregada a la carga desde una fuente con una potencia disponible de\(600\text{ mW}\).
Considera una línea coaxial que esté cortocircuitada en un extremo. El relleno dieléctrico que tiene la línea\(\varepsilon_{r} = 20\) y la línea tiene su resonancia de frecuencia más baja en\(2.4\text{ GHz}\). [Ejemplo de Parallels 2.7.1]
1. ¿Cuál es la longitud de onda guía?
2. Dibuja el circuito equivalente del resonador.
3. ¿Cuál es la longitud física del resonador?
Considere una línea coaxial sin pérdidas que está en circuito abierto en un extremo y se usa como un resonador que es resonante en\(f_{0} = 2.4\text{ GHz}\). El dieléctrico de la línea tiene\(\varepsilon_{r} = 81\). [Ejemplo de Parallels 2.7.2]
1. ¿Cuál es la longitud de onda en la línea?
2. Dibujar el circuito equivalente a elementos grumados de un resonador\(\lambda_{g}/4\) largo?
3. ¿Cuál es la longitud física del resonador?
4. Cuál es la derivada con respecto a la frecuencia de la admitancia del circuito\(LC\) equivalente desarrollada en (b).
5. Si el diámetro del conductor interno de la línea es\(1\text{ mm}\) y el diámetro interior del conductor externo es\(3\text{ mm}\), ¿cuál es la impedancia característica de la línea?
6. Determinar la derivada de frecuencia numérica de la entrada de línea en\(f_{0}\).
7. Derivar los valores del circuito equivalente del resonador en la resonancia.
Desarrollar el modelo de elementos grumados de una línea larga de media longitud de onda con impedancia característica\(Z_{0}\). [Ejemplo de Parallels 2.7.3]
El diámetro del conductor interno de una línea coaxial es\(2\text{ mm}\) y el diámetro interior del conductor externo\(8\text{ mm}\). La línea coaxial está llena de poliimida que tiene una permitividad relativa de\(3.2\).
1. ¿Cuál es la impedancia característica de la línea?
2. Describir las condiciones mediante las cuales se puede soportar un modo no TEM. Se refieren a dos familias diferentes de modos de orden superior.
3. Para la línea coaxial aquí, ¿a qué frecuencia se soportará primero un segundo modo de propagación?

2.12.1 Ejercicios Por Sección

\(†\)desafiante,\(‡\) muy desafiante

\(§2.1\: 1\)

\(§2.2\: 2†, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14†, 15\)

\(§2.3\: 16†, 17, 18‡, 19‡, 20, 21, 22, 23, 24, 25, 26†, 27‡, 28‡, 29, 30†, 31†, 32‡, 33‡, 34†, 35†, 36†, 37, 38, 39, 40, 41, 42, 43\)

\(§2.4\: 44†, 45, 46, 47\)

\(§2.5\: 48‡, 49†, 50†, 51, 52‡, 53\)

\(§2.6\: 54, 55, 56, 57†\)

\(§2.7\: 58, 59†, 60\)

\(§2.9\: 61\)

2.12.2 Respuestas a ejercicios seleccionados

\(11.2\:\Omega\)
\(0.23+\jmath 25\text{ m}^{-1}\)

b)\(74.0\text{ mW}\)

c)\(1.17\text{ cm}\)

(e)\(\jmath 4.55\cdot 10^{-11}\text{ S}\cdot\text{ s}\)

f)\(0.544+\jmath 0.116\)
f)\(41.45\)

\(25\:\Omega\leq Z_{L}\leq 100\:\Omega\)

\(61.2\:\Omega\)

\(354.2\text{ mW}\)