4.2: Características dependientes de la frecuencia

Todas las interconexiones tienen un comportamiento dependiente de la frecuencia. En esta sección se examinan los orígenes del comportamiento dependiente de la frecuencia de una línea de microcinta porque la microcinta tiene la dependencia de frecuencia más significativa entre las interconexiones de interés general. El comportamiento dependiente de la frecuencia distinto del multimodo a menudo resulta en dispersión. El efecto se puede observar en la Figura 4.1.2 para un pulso que viaja a lo largo de una línea. El pulso se extiende a medida que los diferentes componentes de frecuencia viajan a diferentes velocidades. Para una línea larga, los pulsos sucesivos comenzarán a fusionarse y la señal se volverá ininteligible.

Los efectos dependientes de la frecuencia más importantes son

• cambios de las propiedades del material (permitividad, permeabilidad y conductividad) con la frecuencia (Sección 4.2.1),
• Apilamiento de corriente (discutido en la Sección 4.2.3),
• efecto de la piel (Secciones 4.2.4 y 4.2.5),
• variación de inductancia del conductor interno (Sección 4.2.4),
• dispersión dieléctrica (Sección 4.2.6), y
• multimodal (Sección 4.4).

Si bien la discusión se centra en las líneas de microcinta, los efectos ocurren con otras líneas de transmisión planas y no planas.

4.2.1 Dependencia material

Los cambios de permitividad, permeabilidad y conductividad con frecuencia son propiedades de los materiales utilizados. Afortunadamente los materiales de interés en la tecnología de microondas tienen características que son casi independientes de la frecuencia, al menos hasta\(300\text{ GHz}\) aproximadamente.

4.2.2 Distribución de carga dependiente de la frecuencia

El efecto de la piel, el agrupamiento de corriente y la inductancia del conductor interno se deben al retraso necesario en la transferencia de información EM de una ubicación a otra. Esta información no puede viajar más rápido que la velocidad de la luz en el medio. En un material dieléctrico la velocidad de una onda EM será más lenta

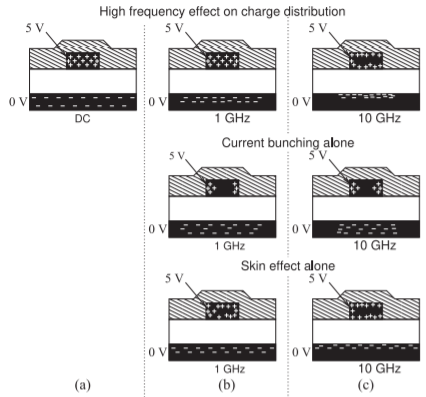
Figura\(\PageIndex{1}\): Vista transversal de la distribución de carga en una interconexión a diferentes frecuencias. Los\(+\) e\(−\) indican concentraciones de carga de diferente polaridad y densidades de corriente correspondientes. No hay corriente de agrupamiento o efecto de piel a DC.

que en el espacio libre por un factor de\(\sqrt{\varepsilon_{r}}\), donde\(\varepsilon_{r}\) está la permitividad relativa del material. Por lo tanto, la velocidad de una onda EM en los dieléctricos de microondas se reduce típicamente por un factor que varía de poco más\(1\) a\(300\). Sin embargo, la velocidad en un conductor es extremadamente baja debido a la alta conductividad. En resumen, el agrupamiento de corriente se debe a cambios relacionados con la velocidad finita de transferencia de información a través del dieléctrico, y el efecto de piel y las variaciones de la inductancia interna del conductor se deben a la muy lenta velocidad de transferencia de información dentro de un conductor. A medida que aumenta la frecuencia, solo se puede enviar información limitada para reorganizar las cargas antes de que la polaridad de la señal se invierta y se envíe información para revertir los cambios. Los efectos de la piel y el agrupamiento de carga en una línea de microcinta se ilustran en sección transversal en la Figura\(\PageIndex{1}\).

4.2.3 Apilamiento de corriente

Considere la distribución de carga para una línea de microcinta que se muestra en las vistas en sección transversal de la Figura\(\PageIndex{1}\). Las secciones transversales de microcinta que se muestran aquí son típicas de una interconexión en una placa de circuito impreso o un circuito integrado monolíticamente donde el dieléctrico superior es una capa de pasivación. El grosor de la microcinta suele ser una fracción significativa de su ancho, aunque esto es exagerado en la Figura\(\PageIndex{1}\).

La distribución de carga que se muestra en la Figura\(\PageIndex{1}\) (a) se aplica cuando hay un voltaje de CC positivo en la tira (el conductor superior). En este caso hay cargas positivas en el conductor superior dispuestas con una distribución bastante uniforme. Las cargas positivas individuales (causadas por la ausencia de electrones de equilibrio que exponen iones cargados positivamente) tienden a repelerse entre sí, pero esto tiene poco efecto en la distribución de carga para conductores prácticos con conductividad finita. (Si el conductor tuviera resistencia cero entonces estas cargas netas quedarían confinadas a la superficie del conductor). El conductor inferior se conoce como el plano de tierra y hay equilibrio

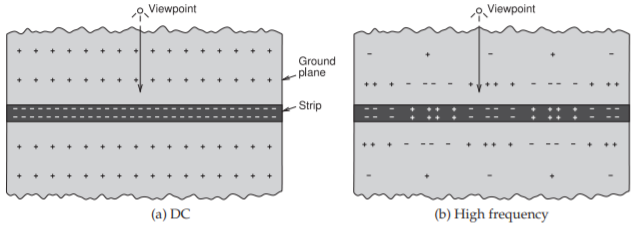
Figura\(\PageIndex{2}\): Efecto de agrupamiento actual en el tiempo. Las cargas positivas y negativas se muestran en la tira y en el plano de tierra. El mirador está en el plano de tierra.

cargas negativas, o un excedente de electrones, de manera que las líneas de campo eléctrico comiencen en las cargas positivas y terminen con las cargas negativas. Las cargas negativas en el plano de tierra se distribuyen uniformemente por todo el plano de tierra. Un punto importante es que donde hay cargas desequilibradas puede haber flujo de corriente. Por lo que la distribución de carga a CC, mostrada en la Figura\(\PageIndex{1}\) (a), indica que para el conductor superior, la corriente fluiría uniformemente dentro de los conductores y la corriente de retorno en el plano de tierra se distribuiría por todo el plano de tierra.

La distribución de carga se vuelve menos uniforme a medida que aumenta la frecuencia y eventualmente la señal cambia tan rápidamente que la información para reorganizar las cargas en el plano de tierra pronto es contrarrestada por instrucciones inversas (medio período último). Por lo tanto, la distribución de carga depende de qué tan rápido cambie la señal. Otra forma de ver este efecto es ver las cargas en la tira de la línea de microcinta a la vez. Esto se muestra en la Figura\(\PageIndex{2}\) para una señal de CC en la línea y para una señal de alta frecuencia. La situación de DC se muestra en la Figura\(\PageIndex{2}\) (a) donde existe una distribución uniforme de las cargas negativas en la tira. Esta distribución uniforme (en este caso de cargas negativas) se ve desde el punto de vista mostrado. Luego, el campo induce cargas positivas distribuidas uniformemente en el plano de tierra. A alta frecuencia las cargas en la tira alternan entre cargas negativas y positivas, como se muestra en la Figura\(\PageIndex{2}\) (b). Ahora la carga efectiva en la tira que se “ve” depende de lo lejos que esté el punto de vista de la franja. Cuando el mirador se encuentra a gran distancia, parecerá que los cargos positivos y negativos se anulan entre sí. Así, en el plano de tierra a una gran distancia de la tira efectivamente habrá muy poca carga neta en la tira. En consecuencia, a distancia, habrá pocas cargas coincidentes en el plano de tierra que coincidan con las cargas en la tira. Más cerca de la franja el suelo “verá” una carga más concentrada en la tira y las cargas en el plano de tierra corresponderán más estrechamente a la situación de DC.

Las líneas de campo eléctrico, que deben originarse y terminar con cargas, se concentrarán en el sustrato más estrechamente debajo de la tira a medida que aumente la frecuencia. Habrá menos líneas de campo eléctrico en el aire que salgan a las cargas menos distantes en el plano de tierra. Los dos efectos principales son que la permitividad efectiva de la línea de microcinta aumenta con la frecuencia, y la pérdida resistiva aumenta a medida que aumenta la densidad de corriente promedio en el suelo, que corresponde a la densidad de carga neta. Así, la resistencia de línea y la capacitancia aumentan con la frecuencia (ver Figura 4.1.1 (a) y 4.1.1 (d), respectivamente). Para la mayoría de los sustratos\(G\) se debe a la relajación dieléctrica más que a la conducción en el dieléctrico. Como tal,\(G\) aumenta linealmente con la frecuencia con un incremento superlineal a frecuencias muy altas cuando el campo eléctrico está más concentrado en el dieléctrico (ver Figura 4.1.1 (c)).

En el dominio de frecuencia los efectos de agrupamiento de corriente se ven en las vistas de mayor frecuencia mostradas en las Figuras\(\PageIndex{1}\) (b y c). (La concentración de cargas cerca de la superficie del metal es un efecto separado conocido como efecto piel). El impacto longitudinal del agrupamiento de corriente o carga solo se ilustra en las Figuras\(\PageIndex{3}\),\(\PageIndex{4}\), y\(\PageIndex{5}\). Estas cifras presentan amplitudes de los fasores de corriente y carga a diversas frecuencias y se calcularon utilizando el simulador Sonnet EM. Al interpretar estas cifras, tomar en cuenta las magnitudes de las distribuciones de corriente y carga identificadas en las leyendas, ya que las escalas se normalizan. Una vista alternativa (o vista en el dominio del tiempo) es la instantánea instantánea de corriente y carga que se muestra en la Figura\(\PageIndex{6}\).

Esta situación no solo se limita al plano transversal, y las regiones más próximas a lo largo de la interconexión también envían instrucciones. El efecto neto es el agrupamiento de cargas y por lo tanto de corriente tanto en el plano de tierra como en la franja.

4.2.4 Efecto Piel e Inductancia Interna del Conductor

A bajas frecuencias, las corrientes se distribuyen uniformemente a lo largo de un conductor. Por lo tanto, hay campos magnéticos dentro del conductor y por lo tanto almacenamiento de energía magnética. Como resultado, hay inductancia interna del conductor. La transferencia de carga al interior de los conductores es particularmente lenta, y a medida que aumenta la frecuencia de la señal, las cargas se confinan más cerca de la superficie del metal. Este efecto se ve en la Figura\(\PageIndex{7}\) donde la densidad de corriente dentro de la tira de una línea de microcinta se traza a diversas frecuencias. Por lo tanto, los campos EM variables en el tiempo no son capaces de penetrar en los conductores tanto como aumenta la frecuencia. Este fenómeno se conoce como el efecto piel. Con corrientes internas menores, la inductancia del conductor interno se reduce y la inductancia total de la línea cae [1, 2, 3, 4]. Así, la redistribución de la corriente da como resultado un cambio de la inductancia con frecuencia (ver Figura 4.1.1 (b)). Solo por encima de unos pocos gigahercios más o menos se puede aproximar la inductancia de la línea como una constante para las dimensiones de interconexión transversal de una micra a varios cientos de micrones.

El efecto piel se caracteriza por la profundidad de la piel\(\delta_{s}\), que es la distancia a la que el campo eléctrico, o equivalentemente la densidad de carga, se reduce a\(1/\text{e}\) de su valor en la superficie. Se determina que la profundidad de la piel es

\[\label{eq:1}\delta_{s}=1/\sqrt{\pi f\mu_{0}\sigma_{2}} \]

Aquí\(f\) está la frecuencia y\(\sigma_{2}\) es la conductividad del conductor. La conductividad es una cantidad medida que está determinada por el mismo fenómeno físico. \(^{1}\)La permitividad y permeabilidad de los metales típicamente utilizados

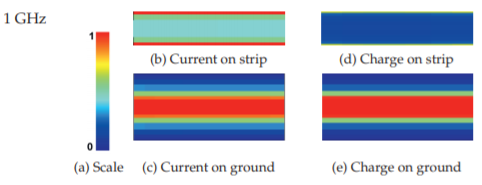
Figura\(\PageIndex{3}\): Corriente normalizada y magnitudes de carga en una línea de microcinta de alúmina a\(1\text{ GHz}\) (\(\varepsilon_{r} = 10.0\)): (a) escala; (b) corriente longitudinal\(i_{z}\),, en la tira (\(10–26\text{ A/m}\)); (c) en el plano de tierra (\(0–3.2\text{ A/m}\)); (d) carga en la tira (\(80–400\text{ nC/m}^{2}\)); y (e) en el suelo (\(0–33\text{ nC/m}^{2}\)). Ver dentro de la contraportada para una imagen en color.

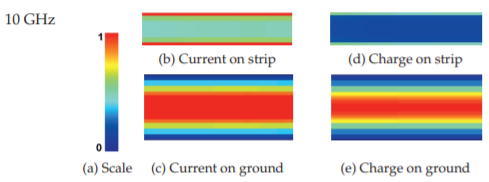
Figura\(\PageIndex{4}\): Corriente normalizada y magnitudes de carga en una línea de microcinta de alúmina a\(10\text{ GHz}\): (a) escala; (b) corriente longitudinal\(i_{z}\),, en la tira (\(10–28\text{ A/m}\)); (c) en el plano de tierra (\(0– 4.1\text{ A/m}\)); (d) carga en la tira (\(114–512\text{ nC/m}^{2}\)); y (e) en el suelo (\(0–39\text{ nC/m}^{2}\)). Ver dentro de la contraportada para una imagen en color.

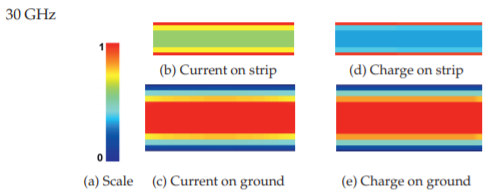
Figura\(\PageIndex{5}\): Magnitudes normalizadas de corriente y carga en una línea de microcinta de alúmina a\(30\text{ GHz}\): (a) escala; (b) corriente longitudinal\(i_{z}\),, en la tira (\(10–31\text{ A/m}\)); (c) en el plano de tierra (\(0–6\text{ A/m}\)); (d) la carga en la tira (\(200–575\text{ nC/m}^{2}\)); y (e) en el suelo (\(0–68\text{ nC/m}^{2}\)). Ver dentro de la contraportada para una imagen en color.

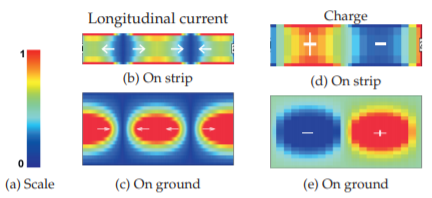
Figura\(\PageIndex{6}\): Corriente instantánea normalizada y carga en una línea de microcinta de alúmina en\(30\text{ GHz}\). Las regiones más ligeras tienen mayor densidad de corriente en (b) y (c), y más carga positiva en (d) y (e).

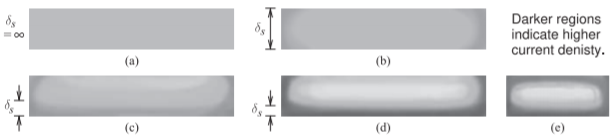
Figura\(\PageIndex{7}\): Secciones transversales de la tira de una línea de microcinta que muestran el impacto del efecto de la piel y el agrupamiento de corriente sobre la densidad de corriente: (a) a dc (densidad de corriente uniforme); (b) el espesor de la tira\(t\),, es igual a la profundidad de la piel,\(\delta_{s}\) (es decir, a baja frecuencia de microondas); (c)\(t = 3\delta_{s}\); ( d)\(t = 5\delta_{s}\) (es decir, a una alta frecuencia de microondas); y (e)\(t = 5\delta_{s}\) para una franja estrecha. Las gráficas son el resultado de simulaciones 3D de una línea de microcinta utilizando rejillas de conductores internos.

para las interconexiones (por ejemplo, oro, plata, cobre y aluminio) son las del espacio libre,\(\varepsilon_{0}\) y\(\mu_{0}\), respectivamente, como no hay mecanismo para almacenar energía eléctrica (no hay separación de centros de carga) y, a excepción de los materiales magnéticos, ningún mecanismo para almacenar energía magnética (no desequilibrada momentos magnéticos).

4.2.5 Efecto Piel y Resistencia a la Línea

El efecto de la piel se ilustra en la Figura\(\PageIndex{1}\) (b) en\(1\text{ GHz}\). La situación es más extrema ya que la frecuencia continúa aumentando (e.g., a\(10\text{ GHz}\)) como en la Figura\(\PageIndex{1}\) (c). Hay varias consecuencias importantes de esto. En el conductor superior, a medida que aumenta la frecuencia, el flujo de corriente se concentra principalmente cerca de la superficie de los conductores y el área de sección transversal efectiva del conductor, en lo que a la corriente se refiere, es menor. Así aumenta la resistencia del conductor superior. Existe una situación más dramática para la distribución de carga en el plano de tierra. De la discusión anterior sobre el agrupamiento actual se observó que la carga no se distribuye uniformemente sobre todo el plano de tierra, sino que se concentra más bajo la franja a medida que aumenta la frecuencia. Además de esto, las cargas y la corriente se limitan a la piel del conductor de tierra de manera que el cambio relativo dependiente de la frecuencia de la resistencia del plano de tierra con frecuencia creciente es mayor que el de la tira. En la tira, el agrupamiento actual da como resultado que las cargas se concentren en los bordes de la tira. Este efecto es más pronunciado cuanto mayor es la permitividad del sustrato.

El efecto piel y el agrupamiento actual dan como resultado la dependencia de la frecuencia de la resistencia de la línea\(R\), con

\[\label{eq:2}R(f)=\left\{\begin{array}{ll}{R(0)}&{f\text{ such that }t\leq 3\delta_{s}}\\{R(0)+R_{\text{skin}}(f)}&{f\text{ such that }t>3\delta_{s}}\end{array}\right. \]

donde\(R(0) = R_{\text{strip}}(0) + R_{\text{ground}}(0)\) está la resistencia de la línea a bajas frecuencias (ver Ecuación (3.5.20)). \(R(f)\)describe la resistencia de la línea dependiente de la frecuencia que se debe tanto al efecto de la piel como al agrupamiento actual. Aproximadamente,

\[\label{eq:3}R_{\text{skin}}(f)=R(0)k\sqrt{f} \]

Aquí\(k\) hay una constante, y mientras Ecuación\(\eqref{eq:3}\) indica proporcionalidad a\(\sqrt{f}\), esta es una aproximación, pero\(R(f)\) siempre aumenta más lentamente que la frecuencia [4, 6, 7, 8]. El punto de interrupción dominante se indica en la Ecuación\(\eqref{eq:2}\).

El aumento de la resistencia de la banda a altas frecuencias resulta tanto del agrupamiento de la corriente, aumentando la densidad de corriente en los bordes de la tira y reduciéndola en el medio con respecto al ancho de la tira, como del efecto piel, aumentando la densidad de corriente en las superficies superior e inferior de la tira y reduciéndola en el medio con respecto al grosor de la tira (esto es motivo de preocupación en frecuencias donde\(t > 3\delta_{s}\) [4, 7]). A bajas frecuencias la contribución del suelo a la resistencia de la línea es pequeña, pero debido al agrupamiento de la corriente la resistencia del suelo se vuelve significativa [8] a frecuencias más altas. La resistencia del suelo aumenta aún más debido al efecto piel y a altas frecuencias de microondas la resistencia del suelo puede ser comparable a la de la tira. La rugosidad superficial del metal también afecta la resistencia de la línea [9]. Esto es fácil de imaginar si la rugosidad es comparable a la profundidad de la piel ya que la trayectoria de la corriente se incrementa por la rugosidad. La rugosidad de la superficie metálica refleja principalmente la rugosidad del sustrato para sustratos duros. Con sustratos blandos, la parte inferior del metal se vuelve rugosa intencionalmente para que la superficie rugosa de metal similar a una aguja penetre y se ancla al dieléctrico cuando el metal y el dieléctrico se presionan juntos. Por estas razones no es posible desarrollar una expresión simple y precisa para la resistencia dependiente de la frecuencia de una línea de microcinta, y también es necesaria la simulación EM, pero incluso entonces no se puede explicar la rugosidad. La simulación EM es necesaria en cualquier caso para determinar la atenuación debida a la radiación. Es esencial incorporar mediciones en el ciclo de diseño de circuitos a altas frecuencias de microondas para dar cuenta de efectos que no pueden modelarse [10, 11]. Una observación sobre la dependencia de frecuencia de la resistencia es que no tiene sentido hacer que el grosor de la tira o del suelo sea más grueso que tres veces la profundidad de la piel.

Ejemplo\(\PageIndex{1}\): Skin Depth

Determinar la profundidad de piel para cobre (Cu), plata (Ag), aluminio (Al), oro (Au), y titanio (Ti) en\(100\text{ MHz},\: 1\text{ GHz},\: 10\text{ GHz},\) y\(100\text{ GHz}\).

Solución

La profundidad de la piel se calcula usando la Ecuación\(\eqref{eq:1}\) y la conductividad del Apéndice 2.A.

Metal	Resistividad \((\text{n}\Omega\cdot\text{m})\)	Conductividad \((\text{MS/m})\)	Profundidad de la piel,\(\delta_{s}\)\((\mu\text{m})\)
			\(100\text{ MHz}\)	\(1\text{ GHz}\)	\(10\text{ GHz}\)	\(100\text{ GHz}\)
Cobre (Cu)	\ ((\ texto {n}\ Omega\ cdot\ texto {m})\) ">\(16.78\)	\ ((\ text {mS/m})\) ">\(59.60\)	\ (\ delta_ {s}\)\((\mu\text{m})\)\(100\text{ MHz}\) “>\(6.52\)	\ (\ delta_ {s}\)\((\mu\text{m})\)\(1\text{ GHz}\) “>\(2.06\)	\ (\ delta_ {s}\)\((\mu\text{m})\)\(10\text{ GHz}\) “>\(0.652\)	\ (\ delta_ {s}\)\((\mu\text{m})\)\(100\text{ GHz}\) “>\(0.206\)
Plata (Ag)	\ ((\ texto {n}\ Omega\ cdot\ texto {m})\) ">\(15.87\)	\ ((\ text {mS/m})\) ">\(63.01\)	\ (\ delta_ {s}\)\((\mu\text{m})\)\(100\text{ MHz}\) “>\(6.34\)	\ (\ delta_ {s}\)\((\mu\text{m})\)\(1\text{ GHz}\) “>\(2.01\)	\ (\ delta_ {s}\)\((\mu\text{m})\)\(10\text{ GHz}\) “>\(0.634\)	\ (\ delta_ {s}\)\((\mu\text{m})\)\(100\text{ GHz}\) “>\(0.201\)
Aluminio (Al)	\ ((\ texto {n}\ Omega\ cdot\ texto {m})\) ">\(26.50\)	\ ((\ text {mS/m})\) ">\(37.74\)	\ (\ delta_ {s}\)\((\mu\text{m})\)\(100\text{ MHz}\) “>\(8.19\)	\ (\ delta_ {s}\)\((\mu\text{m})\)\(1\text{ GHz}\) “>\(2.59\)	\ (\ delta_ {s}\)\((\mu\text{m})\)\(10\text{ GHz}\) “>\(0.819\)	\ (\ delta_ {s}\)\((\mu\text{m})\)\(100\text{ GHz}\) “>\(0.259\)
Oro (Ag)	\ ((\ texto {n}\ Omega\ cdot\ texto {m})\) ">\(22.14\)	\ ((\ text {mS/m})\) ">\(45.17\)	\ (\ delta_ {s}\)\((\mu\text{m})\)\(100\text{ MHz}\) “>\(7.489\)	\ (\ delta_ {s}\)\((\mu\text{m})\)\(1\text{ GHz}\) “>\(2.37\)	\ (\ delta_ {s}\)\((\mu\text{m})\)\(10\text{ GHz}\) “>\(0.749\)	\ (\ delta_ {s}\)\((\mu\text{m})\)\(100\text{ GHz}\) “>\(0.237\)
Titanio (Ti)	\ ((\ texto {n}\ Omega\ cdot\ texto {m})\) ">\(4200\)	\ ((\ text {mS/m})\) ">\(0.2381\)	\ (\ delta_ {s}\)\((\mu\text{m})\)\(100\text{ MHz}\) “>\(103.1\)	\ (\ delta_ {s}\)\((\mu\text{m})\)\(1\text{ GHz}\) “>\(32.6\)	\ (\ delta_ {s}\)\((\mu\text{m})\)\(10\text{ GHz}\) “>\(10.3\)	\ (\ delta_ {s}\)\((\mu\text{m})\)\(100\text{ GHz}\) “>\(3.26\)

Mesa\(\PageIndex{1}\)

4.2.6 Dispersión dieléctrica

La dispersión es principalmente el resultado de que la velocidad de propagación de una señal sinusoidal depende de la frecuencia. Para un pulso en la línea, la dispersión se manifiesta como los diversos componentes de frecuencia de una señal que viaja con diferentes velocidades.

Las líneas de campo eléctrico se desplazan como resultado de las diferentes distribuciones de carga, siendo mayor parte de la energía eléctrica en el dieléctrico a medida que aumenta la frecuencia. Así, la permitividad efectiva de una línea de microcinta aumenta al aumentar la frecuencia. A altas frecuencias, el resultado fundamental del reordenamiento de campo es que la capacitancia de la línea aumenta, pero este cambio puede ser bastante pequeño, típicamente menor que en el\(10\%\) rango de CC a\(100\text{ GHz}\). (Este efecto se describe por la dependencia de frecuencia de la permitividad efectiva de la línea de transmisión). En menor medida, la dispersión también es el resultado de otros parámetros de la línea de transmisión que cambian con la frecuencia, como la resistencia de una interconexión. Para un CI donde las interconexiones pueden tener dimensiones transversales muy pequeñas (por ejemplo, micras) en CI digitales, la resistencia de la línea es la fuente de dispersión más significativa. El efecto cualitativo de la dispersión es el mismo ya sea relacionado con la resistencia (dispersión inducida por resistencia) o cambio en la permitividad efectiva (dispersión inducida por inhomogeneidad dieléctrica).

Las diferentes tecnologías de interconexión tienen diferentes características de dispersión. Por ejemplo, con una línea de microcinta la permitividad efectiva cambia con la frecuencia a medida que cambia la proporción de la energía EM en la región de aire a la de la región dieléctrica. La dispersión se reduce si los campos están localizados y no pueden cambiar la orientación con la frecuencia. Este es el caso de las interconexiones coplanares, en particular, las líneas de guía de ondas coplanares (CPW) y tiras coplanares (CPS). La línea de banda de la Figura 3.3.1 (k) también tiene baja dispersión, ya que los campos están confinados en un medio y la permitividad efectiva es solo la permitividad del medio. Por lo tanto, las elecciones de interconexión pueden tener un efecto significativo en la integridad de una señal que se está transmitiendo.

Como se discutió anteriormente, a medida que aumenta la frecuencia, los campos en una línea de microcinta se concentran más en la región debajo de la tira. Por lo tanto, existe una permitividad de microbanda efectiva dependiente de la frecuencia,\(\varepsilon_{e}(f)\). Esta cantidad aumenta con la frecuencia y la onda se ralentiza progresivamente. La permitividad efectiva de microstrip es ahora

\[\label{eq:4}\varepsilon_{e}(f)=\{c/[v_{p}(f)]\}^{2} \]

Fundamentalmente, caracterizar el problema de dispersión consiste entonces en resolver los campos de la línea de transmisión para la velocidad de fase dependiente de la frecuencia,\(v_{p}(f)\). Los límites de\(\varepsilon_{e}(f)\) se establecen fácilmente; en el extremo de baja frecuencia se reduce al valor TEM estático\(\varepsilon_{e}\) (o\(\varepsilon_{e}(0)\)), mientras que a medida que la frecuencia se incrementa indefinidamente, se\(\varepsilon_{e}(f)\) acerca a la permitividad del sustrato en sí,\(\varepsilon_{r}\). Es decir,

\[\label{eq:5}\varepsilon_{e}(f)\to\left\{\begin{array}{ll}{\varepsilon_{e}(0)}&{\text{as }f\to 0}\\{\varepsilon_{r}}&{\text{as }f\to\infty}\end{array}\right. \]

Entre estos límites\(\varepsilon_{e}(f)\) cambia sin problemas.

4.2.7 Resumen

Diversas tecnologías de línea de transmisión tienen diferentes características de dispersión de frecuencia. Las dos tecnologías más importantes para los circuitos de microondas son las líneas coaxiales y la microcinta. Con ambos, la variación de la resistencia con la frecuencia debida principalmente al efecto de la piel son significativas. Sin embargo, esto tiene poco efecto sobre la impedancia característica y la permitividad efectiva, siendo el efecto dominante una mayor pérdida a frecuencias más altas. Con microcinta, pero no con una línea coaxial, las variaciones debidas al cambio de orientación de los campos EM es el efecto más significativo. Al aumentar la frecuencia la proporción de energía de la señal en la región del aire se reduce y la proporción en el dieléctrico aumenta. La tendencia general con microcinta es que los campos se concentren más en el dieléctrico a medida que aumenta la frecuencia y esto aumenta la permitividad relativa efectiva de una línea de microcinta y, por lo tanto, ralentiza la propagación. La variación de la impedancia característica de la microcinta con la frecuencia es más compleja ya que la rotación transversal cada vez más estrecha, es decir, el rizado, de los campos tiende a aumentar la impedancia característica, pero la permitividad efectiva creciente tiende a disminuir la impedancia característica. Por lo tanto, siguiendo el diseño inicial de un circuito de microcinta, es importante usar simulaciones EM para ajustar diseños para tener en cuenta la dispersión.

Notas al pie

[1] Este fenómeno es descrito por M. Born y E. Wolf [5]. En un conductor un campo eléctrico acelera los electrones libres que a su vez irradian alrededor de la dirección del movimiento. Este proceso se repite a medida que el campo penetra en el conductor. Mientras que el borde de ataque del campo eléctrico se propaga rápidamente a través del conductor, disminuye rápidamente en amplitud. El campo promedio penetra muy lentamente debido a la gran cantidad de electrones libres y la dispersión múltiple del campo. Una guía aproximada es que la velocidad efectiva a frecuencias de microondas para la transferencia de la mayor parte de la energía es aproximadamente\(c/1000\). No es posible determinar un número exacto.