4.6: Limitaciones de Frecuencia Operativa de Microstrip
( \newcommand{\kernel}{\mathrm{null}\,}\)
Diferentes tipos de modos de orden superior pueden existir con microstrip y las dos frecuencias máximas de operación de las líneas de microcinta son (a) el modo TM de orden más bajo y (b) el modo de resonancia de microbanda transversal de orden más bajo. En la práctica, el multimodo es un problema cuando se cumplen dos condiciones. Primero debe ser posible que existan variaciones de campo de orden superior, y segundo, que la energía pueda acoplarse efectivamente al modo de orden superior. Generalmente esto
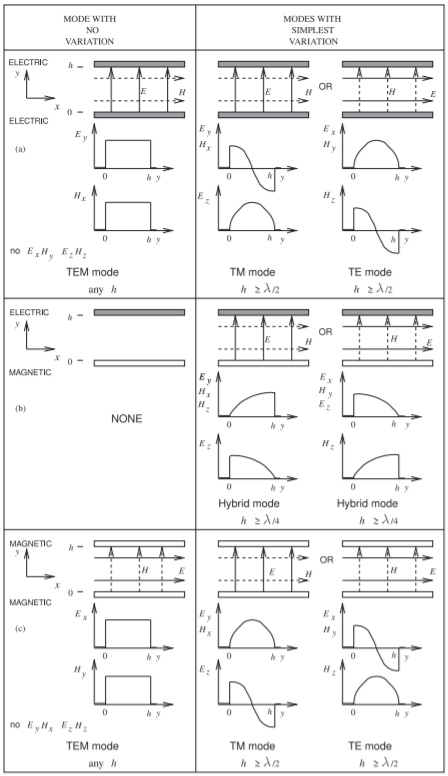
Figura4.6.1: Modos de orden más bajo soportados por combinaciones de paredes eléctricas y magnéticas.
requiere una discontinuidad significativa en la línea o que las velocidades de fase de dos modos coincidan aproximadamente. Una discusión temprana dijo que las velocidades de fase de dos modos serían diferentes y esto es cuando el dieléctrico es uniforme. Sin embargo, con una línea no homogénea como la microcinta, puede haber frecuencias donde las velocidades de fase de dos modos pueden coincidir.
Dado que las discontinuidades son inevitables siempre es una buena idea usar solo la primera consideración. Como se señaló anteriormente, el análisis modal que fue posible con la guía de ondas de placa paralela no se puede repetir fácilmente para la línea de microcinta debido a la sección transversal irregular, pero el fenómeno es muy similar. En lugar de un modo TEM, hay un modo cuasi-TEM y hay modos TE y TM.
4.6.1 Modo dieléctrico de microcinta (modo de losa)
Un dieléctrico en un plano de tierra con una región de aire (de una longitud de onda o más por encima de ella) puede soportar un modo TM, generalmente llamado modo dieléctrico de microcinta, modo sustrato, modo TM microcinta o modo losa. El modo dieléctrico de microcinta es un problema para líneas estrechas de microcinta. Si este modo existe en un entorno de microcinta depende de si se puede acoplar energía desde el modo cuasi-TEM (que siempre se genera) de la línea de microcinta al modo dieléctrico TM. La frecuencia crítica a la que el modo TM se vuelve importante es cuando hay acoplamiento significativo. El acoplamiento es un problema con una línea de microcinta que tiene una tira estrecha, ya que las orientaciones de campo del modo cuasi-tem y el modo dieléctrico se alinean. Además, el acoplamiento ocurre cuando coinciden las velocidades de fase de los dos modos. Un análisis detallado reportado en el Capítulo 11 de [12] y en [13] muestra que esto ocurre en la primera frecuencia crítica,
fc1=ctan−1(εr)√2πh√εr−1
Enfc1 el modo dieléctrico se generará aunque no haya una discontinuidad. Si hay una discontinuidad, digamos una división de una línea de microcinta en dos líneas de microcinta, se producirá multimodo cuando pueda existir el modo dieléctrico. De la Figura4.6.1 (b), el modo de losa dieléctrica puede ser soportado cuandoh>λg/4, dondeλg está la longitud de onda en el dieléctrico. Ahoraλg=λ0/√εr=c/(f√εr), entonces la segunda frecuencia crítica es
fc2=c4h√εr
Este desarrollo supone que la interfaz entre el dieléctrico y el aire forma una buena pared magnética. Con un dieléctrico que tenga una permitividad de10, típica de los circuitos de microondas, el valor efectivo de seh incrementaría hasta en10%. No obstante, es difícil darle un valor exacto a esto.
En resumen,fc2 es la frecuencia más baja a la que existirá el modo dieléctrico si existe una discontinuidad, yfc1 es la frecuencia más baja a la que existirá el modo dieléctrico si no hay una discontinuidad.
La tira de una microtira tiene un ancho de1 mm y se fabrica sobre un sustrato sin pérdidas que es2.5 mm grueso y tiene una permitividad relativa de9. ¿A qué frecuencia ocurre primero el modo de sustrato (o losa)?
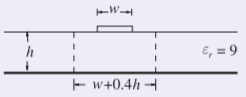
Figura4.6.2
Solución
Se deben considerar dos frecuencias. Uno que proviene de las dimensiones de la losa dieléctrica y el otro de consideraciones de igualación de velocidades de fase. De la consideración de velocidad de fase utilizada en el desarrollo de la ecuación(???), la primera frecuencia crítica es
fc1=ctan−1(εr)√2πh√εr−1=13.9 GHz
La otra frecuencia crítica es cuando se puede soportar una variación del campo magnético o eléctrico entre el plano de tierra y la pared magnética aproximada soportada por la interfaz dieléctrica/espacio libre. Aquí es cuandoh=14λ=λ0/(4√9)=2.5 mm⇒λ0=3 cm. Por lo tanto, la frecuencia crítica del segundo modo de losa es
fc2=10 GHz
Dado que no se pueden evitar las discontinuidades,fc2 es la frecuencia crítica a utilizar.
4.6.2 Modo Microstrip de orden superior
Si las dimensiones de la sección transversal de una línea de microcinta son menores que una fracción de una longitud de onda, entonces las líneas de campo eléctrico y magnético serán como se muestra en la Figura 3.1.2. Estas líneas de campo tienen la mínima variación espacial posible y los campos están confinados casi en su totalidad al plano transversal; a este modo se le llama modo de microcinta cuasi-tem. Sin embargo, a medida que aumenta la frecuencia de la señal en la línea, es posible que estos campos tengan variaciones sinusoidales de un cuarto o medio. Se trata de derivar la frecuencia a la que se soporta un modo de microcinta de orden superior.
A continuación se presenta un resumen de una discusión más completa sobre las limitaciones de frecuencia de operación en la Sección 7.8 de [12]. Algunas variaciones de los campos o modos no se parecen en nada a las orientaciones de campo mostradas en la Figura 3.1.2. Sin embargo, las variaciones más cercanas al modo cuasi-tem se denominan modos de microbanda de orden superior y la que ocurre a la frecuencia más baja corresponde a una variación semisusoidal del campo eléctrico entre el borde de la tira y el plano de tierra. Este camino es un poco más largo que el camino directamente desde la franja hasta el plano de tierra. Sin embargo, para una banda ancha, la mayor parte de la energía EM se encuentra entre la tira y el plano de tierra (ambos son paredes eléctricas) con paredes magnéticas aproximadas en el costado de la tira. Los modos son entonces similares a los modos de guía de ondas de placa paralela descritos en la Sección 1.5. El siguiente modo de microcinta más alto (o modo TE de placa paralela) ocurre cuando puede haber una variación semisinoidal del campo eléctrico entre la tira y el plano de tierra. Esto corresponde a la Figura4.6.1 (a). Sin embargo, para tiras de ancho finito, el primer modo de microbanda de orden superior ocurre a una frecuencia más baja que la implícita en el modelo de guía de ondas de placa paralela. Esto se debe a que los campos de microcinta no se limitan únicamente a la región dieléctrica, y de hecho las líneas de campo eléctrico no siguen la distancia más corta entre la banda y el plano de tierra. Así, los campos a lo largo de las trayectorias más largas a los lados de la tira pueden variar a una frecuencia menor que en la trayectoria directa. Con modelado EM detallado y con soporte experimental se ha establecido que el primer modo de microbanda de orden superior puede existir en frecuencias mayores a [12]
fHigher-Microstrip=c4h√εr−1
Esto es, sin embargo, sólo una guía aproximada.
La tira de una microtira tiene un ancho de1 mm y se fabrica sobre un sustrato sin pérdidas que es2.5 mm grueso y tiene una permitividad relativa de9. ¿A qué frecuencia se propaga primero el primer modo de microcinta superior?
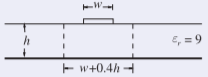
Figura4.6.3
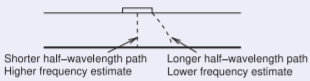
Figura4.6.4
Solución
El modo de microbanda de orden superior ocurre cuando se puede soportar una variación de media longitud de onda del campo eléctrico entre la tira y el plano de tierra. Cuandoh=λ/2=λ0/(3⋅2)=2.5 mm; es decir, el modo ocurrirá cuándoλ0=15 mm. Entonces
fHigher-Microstrip=20 GHz
Una mejor estimación de la frecuencia donde el modo de microcinta de orden superior se convierte en un problema viene dada por la ecuación(???):
fHigher-Microstrip=c/(4h√εr−1)=10.6 GHz
Por lo que se han calculado dos estimaciones para la frecuencia a la que puede existir primero el primer modo de microcinta de orden superior. La primera estimación es aproximada y se basa en una variación de media longitud de onda del campo eléctrico confinado a la trayectoria directa entre la banda y el plano de tierra. La segunda estimación es más precisa ya que considera que en el borde de la franja los campos siguen un camino más largo hasta el plano de tierra. Es la variación de media longitud de onda en esta ruta más larga la que determina si existirá el modo de microbanda de orden superior. Así, la determinación más precisa produce una menor frecuencia crítica.
4.6.3 Resonancia Transversal de Microstrip
Para una línea de microcinta ancha, puede existir un modo de resonancia transversal. Este es el modo que ocurre cuando la energía EM rebota entre los bordes de la tira con la discontinuidad en los bordes de la tira formando un límite débil. Esto se ilustra en la Figura4.6.5, donde la microcinta mostrada en sección transversal en la Figura4.6.5 (a) se aproxima como una guía de ondas rectangular en la Figura4.6.5 (b) con paredes magnéticas en los lados y una pared eléctrica extendida en la superficie superior del dieléctrico. La Figura4.6.5 (b) se llama el modelo de guía de ondas de microcinta. El modo de resonancia transversal corresponde a la variación deH campo de orden más bajo entre las paredes magnéticas. A la frecuencia de corte para este modo de resonancia transversal, el circuito equivalente es una línea de transmisión resonante de longitudw+2d, como se muestra en la Figura4.6.6, donde dad=0.2h cuenta de la franja lateral de microcinta. Una longitud de media longitud de onda debe ser soportada por la longitudw+2d. Por lo tanto, la media longitud de onda de corte es
λc2=w+2d=w+0.4hthat isc2fc√εr=w+0.4h
De ahí que la frecuencia crítica para la resonancia transversal es
fc, TRAN=c√εr(2w+0.8h)
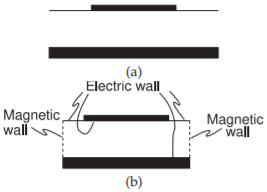
Figura4.6.5: Aproximación de una línea de microcinta como guía de ondas: (a) sección transversal de microcinta; y (b) modelo de guía de ondas de microcinta que tiene ancho efectivow+0.4h con paredes magnéticas y eléctricas.
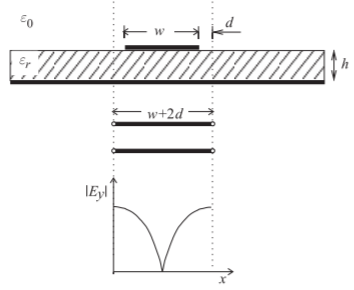
Figura4.6.6: Resonancia transversal: onda estacionaria (|Ey|) y línea de transmisión equivalente de longitudw+2d, donded=0.2h.
La tira de una microtira tiene un ancho de1 mm y se fabrica sobre un sustrato sin pérdidas que es2.5 mm grueso y tiene una permitividad relativa de9.
- ¿A qué frecuencia ocurre primero la resonancia transversal?
- ¿Cuál es el rango de frecuencia de operación de la línea de microcinta?
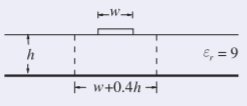
Figura4.6.7
Solución
h=2.5 mm,w=1 mm,λ=λ0/√εr=λ0/3
- El modelo de guía de onda magnética de la Figura se4.6.5 puede utilizar para estimar la frecuencia a la que esto ocurre. La frecuencia a la que se produce el primer modo de resonancia transversal es cuando hay una variación completa de media longitud de onda del campo magnético entre las paredes magnéticas, es decir, cuandow+0.4h=λ/2=2 mm:
λ03⋅2=2 mm⇒λ0=12 mmand sofc, TRAN=25 GHz - Todas las frecuencias multimodales críticas deben considerarse aquí y tomar el mínimo: para el modo losa,fc1 (Ecuación(???)) yfc2 (Ecuación(???), ver Ejemplo4.6.1 para el cálculo de estas); para el modo de microbanda de orden superior, fHigh−Microstrip (Ecuación (???), ver Ejemplo4.6.2 para este cálculo)); y para el modo de resonancia transversal (Ecuación(???), y calculado en este ejemplo). Entonces el rango de frecuencia de operación es de CC a10 GHz.
4.6.4 Resumen
Hay cuatro modos principales de orden superior que deben considerarse con líneas de transmisión de microcinta:
| Modo | Frecuencia Crítica |
|---|---|
| Modo dieléctrico (o sustrato) sin discontinuidad | Ecuación(???) |
| Modo dieléctrico (o sustrato) con discontinuidad | Ecuación(???) |
| Modo de microcinta de orden superior | Ecuación(???) |
| Modo de resonancia transversal | Ecuación(???) |
Mesa4.6.1
La frecuencia más baja determina la frecuencia superior de operación de la línea de transmisión con un solo modo.


