3.2: Líneas acopladas paralelas
- Page ID
- 85228
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Varias de las ventajas clave de los filtros de línea acoplada sobre otros filtros distribuidos es que el acoplamiento entre resonadores puede ser fuerte si el par de resonadores de línea acoplada están cerca uno del otro, o bajo si están ampliamente separados. Esto permite que los filtros se realicen con\((2–10\%)\) anchos de banda altos\((30–70\%)\)\((10–30\%)\), medios o bajos. Los filtros de ancho de banda bajo requieren un acoplamiento bajo de los resonadores, mientras que los filtros de ancho de banda alto requieren un acoplamiento alto. Los filtros de línea acoplada también son compactos y se pueden implementar en configuraciones de microcinta o en la mayoría de las otras tecnologías de línea de transmisión. Las diferentes formas de línea de transmisión tienen diferentes\(Q\) s. Las líneas de transmisión planas tienen\(Q\) s moderadas especialmente a altas frecuencias, debido principalmente a
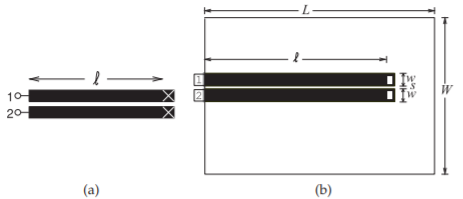
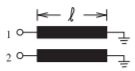
Figura\(\PageIndex{1}\): Disposición de línea de microcinta acoplada: (a) esquema; y (b) disposición en un simulador EM. Las dimensiones de las líneas acopladas son\(w = 500\:\mu\text{m}\)\(s = 100\:\mu\text{m}\),\(\ell = 1\text{ cm}\),\(W = 6\text{ mm}\), y\(L = 12\text{ mm}\). El metal es oro\(6\:\mu\text{m}\) grueso (conductividad\(\sigma = 42.6\times 10^{6}\text{ S/m}\)) y la altura del sustrato de alúmina es\(600\:\mu\text{m}\) con permitividad relativa\(\varepsilon_{r} = 9.8\) y tangente de pérdida de\(0.001\).
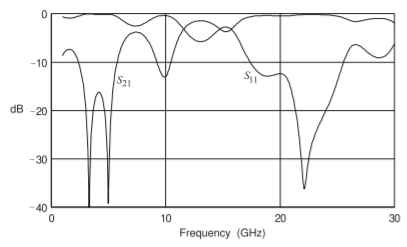
Figura\(\PageIndex{2}\): Pérdida de inserción\((S_{21})\) y pérdida\((S_{11})\) de retorno de la línea acoplada de la Figura\(\PageIndex{1}\) con un\(s = 100\:\mu\text{m}\) hueco.
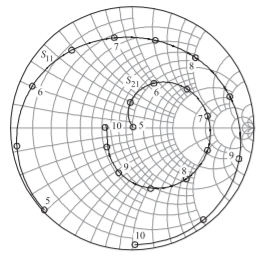
Figura\(\PageIndex{3}\): Pérdida de inserción y pérdida de retorno en un rango de frecuencia estrecho trazado en una gráfica de Smith. La anotación en los marcadores es la frecuencia en GHz.
campos radiados. Bajo\(Q\) significa que la pérdida de inserción de los filtros será alta y los faldones de filtro no serán tan empinados como lo serían si se utilizara una estructura de línea de\(Q\) transmisión alta. Por ejemplo, hasta principios de la década de 2000 los filtros de RF en la parte frontal de los teléfonos celulares eran en su mayoría filtros Chebyshev de séptimo orden que usaban líneas de losa acopladas como se muestra en la Figura\(\PageIndex{8}\) (aunque aquí solo
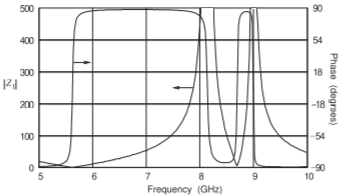
Figura\(\PageIndex{4}\): Impedancia de entrada en el Puerto\(1\) de las líneas de microcinta acopladas en la Figura\(\PageIndex{1}\). Puerto\(2\) se termina en\(50\:\Omega\).
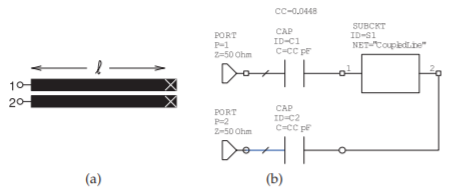
Figura\(\PageIndex{5}\): Líneas de microcinta acopladas capacitivamente: (a) esquemáticas; y (b) representación en una herramienta CAD de microondas con un subcircuito que representa las líneas acopladas. El diseño del subcircuito se muestra en la Figura\(\PageIndex{1}\).
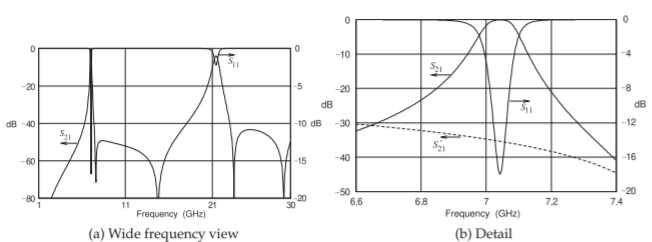
Figura\(\PageIndex{6}\): Pérdida de retorno y pérdida de inserción cuando los capacitores de acoplamiento están\(44.8\text{ fF}\). Esto da como resultado una respuesta similar a Butterworth. \(S_{21}'\)es la respuesta sin\(C_{1}\) y\(C_{2}\).
se muestran cuatro resonadores para mayor claridad). Por lo general, las placas superior e inferior de los resonadores estaban\(2–3\text{ mm}\) separadas y el área del filtro de slabline estaba\(1\text{ cm}\times 1\text{ cm}\). Esto es demasiado grande para los teléfonos inteligentes delgados de hoy. No obstante, son muy buenos filtros y baratos de producir. El procedimiento de diseño eléctrico para los filtros de línea de losa acoplados en paralelo y para el uso de otras estructuras de línea de transmisión es el mismo que para los filtros de microcinta acoplados en paralelo. La diferencia está sólo en la implementación física final.
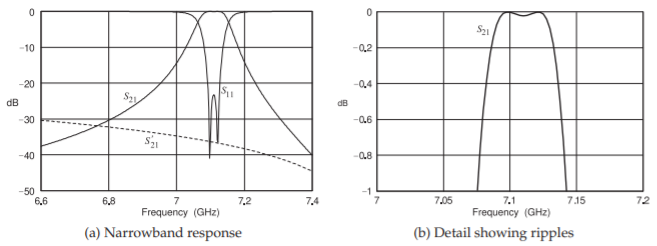
Figura\(\PageIndex{7}\): Pérdida de retorno y pérdida de inserción cuando los capacitores de acoplamiento están\(37.6\text{ fF}\). Esto da como resultado una respuesta similar a Chebyshev-como. \(S_{21}'\)es la respuesta sin\(C_{1}\) y\(C_{2}\).
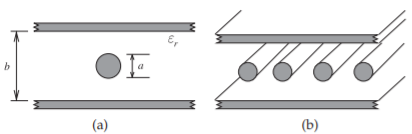
Figura\(\PageIndex{8}\): Línea de losa: (a) sección transversal de una sola línea de losa; y (b) configuración de línea acoplada paralela con cuatro lmeas acopladas.
3.2.1 Configuraciones de línea acopladas
La configuración de línea acoplada considerada en el Ejemplo 3.1.1 se denomina sección combline. Esta es una de las muchas que tienen respuestas selectivas de frecuencia deseables. Las características de muchas configuraciones de líneas acopladas paralelas que tienen características de paso de banda, paso total o parada total se muestran en la Tabla\(\PageIndex{1}\). Las configuraciones más importantes son las estrelladas\((⋆)\).
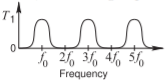
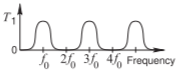
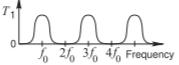
La sección PCL de Filtro (a) en la Tabla\(\PageIndex{1}\) se denomina sección interdigital y es un filtro de paso de banda. El filtro dual es Filtro (b), con lo que se llama una sección acoplada paralela, y ambos pueden usarse para realizar filtros de ancho de banda estrecho\((2–3\%)\) a ancho (hasta\(30\%\)) con respuestas cercanas a simétricas alrededor de la frecuencia central\(f_{0}\). Para un filtro de ancho de banda amplio las líneas están cerca y para un filtro de ancho de banda estrecho las líneas paralelas están ampliamente separadas para que haya acoplamiento de bajo nivel. El filtro (c) también es un filtro de paso de banda, sin embargo, la selectividad de frecuencia no es tan buena como con los Filtros (a) y (b). Los filtros (d), (e) y (f) son filtros de paso total. Estos filtros se utilizan para ajustar la fase de una señal transmitida, generalmente para acomodar la dispersión de fase (por ejemplo, variación de fase con respecto a la frecuencia) que se introdujo en otro lugar. Si bien esta función analógica alguna vez fue importante, lo es menos ahora ya que las técnicas DSP suelen igualar suficientemente la fase. El filtro (g) es un filtro allstop, lo que significa que se transmite una señal insignificante. Este filtro no tiene ningún uso práctico. Los filtros (h) e (i) son intrínsecamente filtros todo-stop. Un ejemplo de la respuesta de la sección de combline de Filtro (h) se vio en la Figura\(\PageIndex{2}\) de Ejemplo\(\PageIndex{1}\), donde la respuesta de todo-stop se centra en\(4\text{ GHz}\). La respuesta es demasiado amplia para ser útil como filtro bandstop (en cualquier aplicación práctica).
| Atributos | Circuito | Respuesta |
|---|---|---|
| \(⋆\)a) Sección interdigital. Paso de banda. Ancho de banda estrecho a ancho. \(\ell = \lambda /4\)en\(f_{0}\). Banda de paso simétrica. |  |
 |
| \(⋆\)b) Sección acoplada paralela. Paso de banda. Ancho de banda estrecho a ancho. \(\ell = \lambda /4\)en\(f_{0}\). Banda de paso simétrica. |  |
 |
| (c) Paso de banda. Ancho de banda moderado a amplio. \(\ell = \lambda /4\)en\(f_{0}\). | 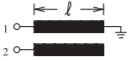 |
 |
| (d) Pase total. \(0 <\ell ≤ \lambda /2\)en\(f_{0}\). |  |
 |
| (e) Pase total. \(0 <\ell ≤ \lambda /2\)en\(f_{0}\). |  |
 |
| (f) Pase total. \(0 <\ell ≤ \lambda /2\)en\(f_{0}\). |  |
 |
| (g) All-stop (sin uso práctico). |  |
|
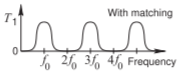
| \(⋆\)h) Sección Combline. All-stop sin emparejar. Paso de banda con coincidencia. Ancho de banda moderado a amplio. \(\ell = \lambda /4\)en\(f_{0}\). Compacto. Respuesta asimétrica. |  |
 |
| (i) All-stop sin emparejar. Paso de banda con coincidencia. Ancho de banda moderado a amplio. \(\ell = \lambda /4\). Compacto. Respuesta asimétrica. |  |
 |
Tabla\(\PageIndex{1}\): Respuestas de las nueve configuraciones de líneas acopladas con ancho de banda estrecho\((2–3\%)\)\((3– 10\%)\), moderado y ancho de\((10\%–30\%)\) banda. Las configuraciones más importantes son las estrelladas\((⋆)\).
Sin embargo, con una coincidencia mínima, como un condensador en serie en cada uno de los puertos (ver Figura\(\PageIndex{5}\)), la sección de combline se convierte en un filtro pasabanda muy bueno (ver Figuras\(\PageIndex{6}\) y\(\PageIndex{7}\)). El filtro de paso de banda combline, Filter (h), es más compacto que los Filtros (a) y (b). Sin embargo, tiene una respuesta de paso de banda asimétrica (que se puede ver en la Figura\(\PageIndex{7}\) (a)), mientras que los Filtros (a) y (b) tienen una respuesta de frecuencia simétrica. El tipo de respuesta que se prefiere depende de la aplicación. Filtro (i) es el dual de Filtro (h), pero en la práctica
| Atributos | Circuito | Respuesta |
|---|---|---|
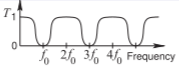
| \(⋆\)(j) Paso bajo. Ancho de banda estrecho a moderado. \(\ell = \lambda /2\)en\(f_{0}\). | 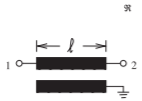 |
 |
| \(⋆\)(k) Paso bajo. Ancho de banda estrecho a moderado. \(\ell = \lambda /4\)en\(f_{0}\). | 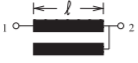 |
 |
| \(⋆\)(l) Paso bajo. Ancho de banda estrecho. \(\ell = \lambda /4\)en\(f_{0}\). | 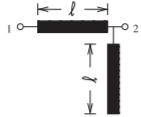 |
 |
| \(⋆\)(m) Tope de banda. Ancho de banda estrecho. \(\ell = \lambda /4\)en\(f_{0}\). | 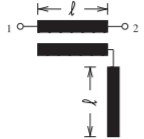 |
 |
Tabla\(\PageIndex{2}\): Respuestas de configuraciones de líneas acopladas que tienen respuestas de paso bajo y de parada de banda.
se prefiere la configuración de combline de Filter (h).
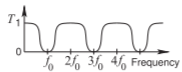
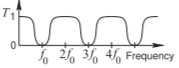
La tabla\(\PageIndex{2}\) presenta secciones de líneas acopladas que tienen respuestas de paso bajo y de parada de banda. Todos estos filtros tienen características deseables y así todos están estrellados\((⋆)\). El filtro (l) no es un filtro PCL pero se usa en compensación entre los tres filtros de paso bajo (es decir, Filtros (j), (l) y (m)). La aplicación habitual de un filtro de tope de banda es entallar una señal no deseada (por ejemplo, para evitar que aparezca un LO donde no se desea). Como tal, la respuesta de frecuencia deseada es de banda estrecha y Filter (m) es una buena opción para un filtro bandstop.
El diseño del filtro usando secciones PCL comienza con la elección de una configuración PCL que tiene la respuesta de frecuencia deseada esencial. Cada una de las secciones PCL en Tablas\(\PageIndex{1}\) y\(\PageIndex{2}\) tiene dos resonadores y puede implementar filtros pasabanda, bandstop y paso bajo que tienen respuestas de segundo orden. \(^{1}\)Para cumplir con las especificaciones generalmente es necesario replicar la sección básica. Por lo tanto, al tratar las dos configuraciones de resonador como celdas unitarias, se puede realizar un filtro multicelular. Las formas multicelulares de las configuraciones principales de paso de banda se muestran en la Tabla\(\PageIndex{3}\). La implementación multicelular de la interdigital, paralela
| Nombre | Celda Unitaria | Forma Multicélula |
|---|---|---|
| (a) Filtro de paso de banda interdigital. \(\ell = \lambda /4\). |  |
 |
| (b) Filtro de paso de banda acoplado a bordes paralelos. \(\ell = \lambda /4\). |  |
 |
| (c) Filtro de paso de banda en horquilla de borde paralelo. \(\ell > \lambda /4\). |  |
 |
|
d) Filtro pasabanda Combline. \(\ell = \lambda /4\). Se requiere coincidencia.
|
 |
 |
|
(e) Filtro de paso de banda Combline con banda de detención extendida. \(\ell = \lambda /4\). \(\ell_{2}\approx \lambda /8\)(típicamente). Se requiere coincidencia.
|
 |
 |
Tabla\(\PageIndex{3}\): Formas multicelulares de configuraciones de líneas acopladas paralelas de paso de banda. La longitud de onda\(\lambda\),, está en la frecuencia central del filtro.
filtros de paso de banda acoplados a bordes, (a) y (b) en Tablas\(\PageIndex{3}\), es sencillo. Se muestra una variación en el Filtro (c), que pliega las secciones paralelas acopladas a bordes para realizar una forma compacta multicelda llamada filtro horquilla [1, 2, 3]. Una de las consecuencias de usar segmentos de línea de transmisión para realizar un filtro es que hay bandas de paso espurias. Esto se debe a que una\(\lambda /4\) sección de línea se ve igual eléctricamente que una\(3\lambda /4\) sección. En consecuencia, normalmente hay bandas de paso espurias en las frecuencias armónicas impares. Si el resonador básico es\(\lambda /2\) largo, entonces las bandas de paso espurias estarían en todas las frecuencias armónicas. Una solución es incorporar capacitores en el
Figura\(\PageIndex{9}\): Modelo de red de un par de líneas acopladas.
resonadores como se muestra en el Filtro (e) en la Tabla\(\PageIndex{3}\) [2, 4, 5]. Así, cada uno de los resonadores originales de línea de transmisión ahora se convierte en una combinación de un condensador y un segmento de línea de transmisión más corto. Si el nuevo segmento de línea de transmisión es\(\lambda /8\) largo, la primera banda de paso espuria ahora estará en\(5f_{0}\) lugar de\(3f_{0}\). Las bandas de paso espurias se pueden empujar más arriba en frecuencia mediante el uso de longitudes de línea de transmisión aún más cortas, pero el rendimiento del filtro en la frecuencia de banda de paso\(f_{0}\),, se verá comprometido.
Existen muchas variaciones en el filtro PCL y se han desarrollado varias técnicas de diseño diferentes [6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28]. Consulte estas citas para explorar configuraciones alternativas de PCL y métodos de diseño alternativos a los que se presentan aquí. Este capítulo presenta uno de los enfoques comunes para sintetizar filtros PCL y el esquema acomoda el uso de carga capacitiva utilizada para extender la banda de parada de un filtro de banda de paso.
Antes de lanzarse al procedimiento de síntesis para un filtro PCL, se justifica un comentario sobre síntesis versus optimización. Con una topología simple como las topologías de filtro de segundo orden que se muestran en la Tabla\(\PageIndex{1}\), se podría utilizar un procedimiento de optimización para diseñar los anchos y longitudes de las líneas y las dos o cuatro variables que describen las redes de coincidencia externas requeridas que no se muestran. Una optimización global es ciertamente factible. Sin embargo, no es factible utilizar la optimización global de, por ejemplo, un filtro de séptimo orden requerido para cumplir con las especificaciones típicas del teléfono celular. Una excepción es si un diseño para una especificación muy similar está disponible y los cambios requeridos son pequeños. El diseño competitivo del filtro requiere síntesis. Esto conducirá a un rendimiento óptimo, y la información obtenida se puede utilizar en modificaciones de topología.
3.2.2 Modelos de circuitos de línea acoplada
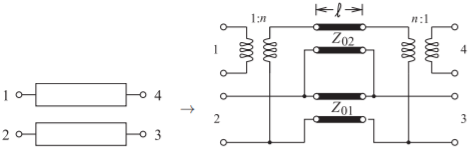
En la Sección 5.9.5 de [29] se presentó un modelo aproximado de líneas acopladas de un par de líneas acopladas. Este modelo se repite en la Figura\(\PageIndex{9}\). Los parámetros del modelo de red están relacionados con las impedancias del modelo de la siguiente manera:
\[\label{eq:1}n=\frac{1}{K}=\frac{Z_{0e}+Z_{0o}}{Z_{0e}-Z_{0o}} \]
\[\label{eq:2}Z_{0S}=\sqrt{(Z_{02}Z_{0o})} \]
\[\label{eq:3}Z_{01}=\frac{Z_{0S}}{\sqrt{1-K^{2}}} \]
\[\label{eq:4}Z_{02}=Z_{0S}\frac{\sqrt{1-K^{2}}}{K^{2}} \]
Diversas disposiciones de terminación de las líneas acopladas dan como resultado varios elementos de filtro útiles. Una disposición se muestra en la Figura\(\PageIndex{10}\). También se muestra en esta figura el desarrollo del modelo de red basado en el modelo de la figura\(\PageIndex{9}\). El modelo de red final es una línea de transmisión de impedancia característica\(Z_{01}\) en cascada con un stub de circuito abierto. Considera lo que sucede a la frecuencia resonante,\(f_{r}\) (la frecuencia a la que las líneas tienen un cuarto de longitud de onda). A frecuencias más bajas,\(f ≪ f_{r}\), la\(Z_{02}\) línea
Figura\(\PageIndex{10}\): Sección de red distribuida de paso bajo derivada de un par de líneas acopladas con puerto de\(1\) circuito abierto. El circuito abierto está indicado por un nodo (círculo abierto) con una línea a través del mismo. El modelo de red final es una línea de transmisión de impedancia característica\(Z_{01}\) y un stub de circuito abierto de impedancia característica\(Z_{02}\). Las líneas y los talones tienen un cuarto de longitud de onda en la frecuencia de la esquina. (Así con el stub\(f_{r} = f_{0}\), y la impedancia característica del stub es como se muestra.)
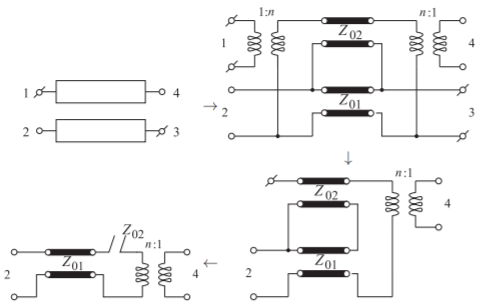
Figura\(\PageIndex{11}\): Sección paralela de línea acoplada con puertos\(1\) y modelos de\(3\) circuito abierto y de red. (Para el stub, se muestra la impedancia característica del stub y\(f_{r} = f_{0}\).)
es un circuito abierto y las señales viajan a lo largo\(Z_{01}\). En resonancia el\(Z_{02}\) stub se convierte en un cortocircuito y las señales no pasan. Esta es una cruda verificación de que se trata de una estructura de paso bajo. El proceso es visual y se espera que se explique por sí mismo. Otros ejemplos se muestran en las Figuras\(\PageIndex{11}\) a\(\PageIndex{13}\).
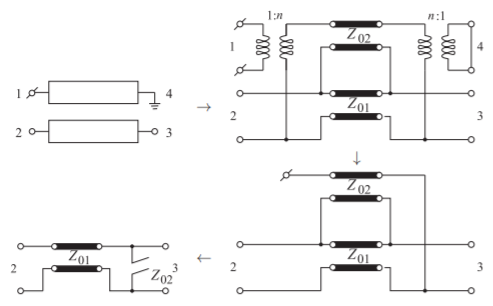
El modelo de una sección de combline se muestra en la Figura\(\PageIndex{13}\). La reducción final de red se repite en la Figura\(\PageIndex{14}\), y se mostrará que el modelo en la Figura\(\PageIndex{14}\) (b) es equivalente al modelo de la Figura\(\PageIndex{14}\) (a). En la síntesis de un filtro combline, se obtiene la red de la Figura\(\PageIndex{14}\) (b) y ésta puede ser
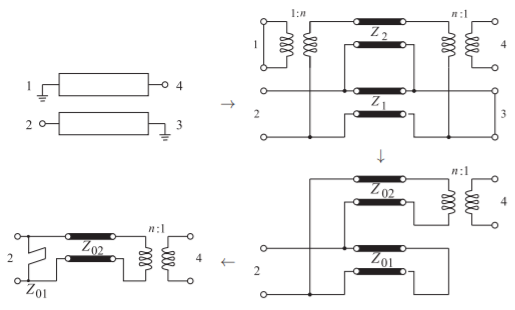
Figura\(\PageIndex{12}\): Sección interdigital y modelos de red. (Para el stub, se muestra la impedancia característica del stub y\(f_{r} = f_{0}\).)
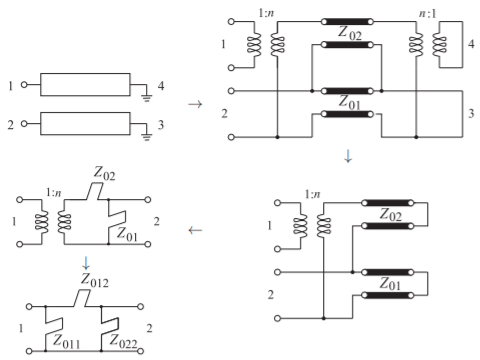
Figura\(\PageIndex{13}\): Sección Combline y modelos de red. (Para los stubs, se muestran las impedancias características de los stubs y\(f_{r} = f_{0}\).)
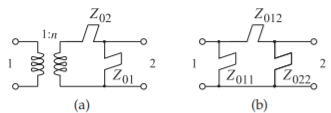
Figura\(\PageIndex{14}\): Modelos equivalentes de una sección de combline. (Para los stubs, se muestran las impedancias características de los stubs y\(f_{r} = f_{0}\).)
relacionados de nuevo con las dimensiones de la línea acoplada. La equivalencia se realiza utilizando\(ABCD\) parámetros y, como se verá, la equivalencia no será a una sola frecuencia sino que será de banda ancha. Los\(ABCD\) parámetros de la red en la Figura\(\PageIndex{14}\) (a) se obtienen mediante la conexión en cascada de\(ABCD\) los parámetros de tres dos puertos (cuyos\(ABCD\) parámetros se dan en la Tabla 2.4.1 de [30]). Los\(ABCD\) parámetros de la red en la Figura\(\PageIndex{14}\) (a) son (a partir de la multiplicación de tres matrices de\(ABCD\) parámetros)
\[\begin{align} \label{eq:5}T_{A}&=T_{\text{TRANSFORMER}}T_{\text{SERIES STUB}}T_{\text{SHUNT STUB}} \\ \label{eq:6} &=\left[\begin{array}{cc}{1/n}&{0}\\{0}&{n}\end{array}\right]\left[\begin{array}{cc}{1}&{\jmath Z_{02}\tan\theta}\\{0}&{1}\end{array}\right]\left[\begin{array}{cc}{1}&{0}\\{-\jmath /(Z_{01}\tan\theta)}&{1}\end{array}\right] \\ \label{eq:7}&=\left[\begin{array}{cc}{1/n}&{\jmath Z_{02}\tan\theta /n} \\ {0}&{n}\end{array}\right]\left[\begin{array}{cc}{1}&{0}\\{-\jmath /(Z_{01}\tan\theta)}&{1}\end{array}\right] \\ \label{eq:8}&=\left[\begin{array}{cc}{\frac{1}{n}\left(1+\frac{Z_{02}}{Z_{01}}\right)}&{\jmath Z_{02}\tan\theta /n}\\{-\jmath n/(Z_{01}\tan\theta)}&{n}\end{array}\right]\end{align} \]
Los\(ABCD\) parámetros de la red en la Figura\(\PageIndex{14}\) (b) son
\[\begin{align}\label{eq:9}T_{B}&=T_{\text{SHUNT STUB}}T_{\text{SERIES STUB}}T_{\text{SHUNT STUB}} \\ \label{eq:10}&=\left[\begin{array}{cc}{1}&{0}\\{-\jmath /(Z_{011}\tan\theta )}&{1}\end{array}\right]\left[\begin{array}{cc}{1}&{\jmath Z_{012}\tan\theta}\\{0}&{1}\end{array}\right]\left[\begin{array}{cc}{1}&{0}\\{-\jmath /(Z_{022}\tan\theta)}&{1}\end{array}\right] \\ \label{eq:11}&=\left[\begin{array}{cc}{1}&{\jmath Z_{012}\tan\theta}\\{-\jmath /(Z_{011}\tan\theta)}&{1+Z_{012}/Z_{011}}\end{array}\right]\left[\begin{array}{cc}{1}&{0}\\{-\jmath (Z_{022}\tan\theta)}&{1}\end{array}\right] \\ \label{eq:12} &= \left[\begin{array}{cc}{1+\frac{Z_{012}}{Z_{022}}}&{\jmath Z_{012}\tan\theta}\\{\frac{-\jmath}{\tan\theta}\left(\frac{1}{Z_{011}}+\frac{1}{Z_{022}}+\frac{Z_{012}}{Z_{011}Z_{022}}\right)}&{1+\frac{Z_{012}}{Z_{011}}}\end{array}\right] \end{align} \]
Ecuación de ecuaciones\(\eqref{eq:8}\) y\(\eqref{eq:12}\) rendimientos
\[\begin{align}\label{eq:13}1+\frac{Z_{012}}{Z_{022}}&=\frac{1}{n}\left(1+\frac{Z_{02}}{Z_{01}}\right) \\ \label{eq:14} Z_{012}&=Z_{02}/n \\ \label{eq:15}\left(\frac{Z_{011}+Z_{022}+Z_{012}}{Z_{011}Z_{022}}\right)&=\frac{n}{Z_{01}} \\ \label{eq:16}1+\frac{Z_{012}}{Z_{011}}&=n\end{align} \]
que tienen la solución
\[\begin{align}\label{eq:17}Z_{011}&=\frac{Z_{012}}{n-1}=\frac{Z_{02}}{n(n-1)} \\ \label{eq:18}Z_{012}&=\frac{Z_{02}}{n} \\ \label{eq:19}Z_{022}&=\frac{Z_{01}Z_{02}}{Z_{02}-(n-1)Z_{01}}\end{align} \]
Reordenando estas, expresiones para\(Z_{01},\: Z_{02},\) y se\(n\) pueden obtener:
\[\label{eq:20}n=1+\frac{Z_{012}}{Z_{011}},\quad Z_{01}=\left(\frac{nZ_{011}Z_{022}}{Z_{011}+Z_{022}+Z_{012}}\right),\quad\text{and}\quad Z_{02}=nZ_{02}Z_{012} \]
Usando estas, Ecuaciones\(\eqref{eq:1}\) —\(\eqref{eq:4}\), y el análisis de línea acoplada de la Sección 5.6 de [29], se pueden obtener los parámetros geométricos de la sección de línea combinada correspondiente al circuito stub de la Figura\(\PageIndex{14}\) (b).
Así, el circuito equivalente de la sección de combline, la figura superior izquierda en la figura\(\PageIndex{13}\), tiene el circuito equivalente que se muestra en la figura\(\PageIndex{14}\). La síntesis de filtros puede dirigirse al desarrollo de estructuras de circuitos como la de la Figura\(\PageIndex{14}\) (b) y a partir de este diseño eléctrico, se puede desarrollar el diseño físico que consiste en secciones de combline.
Notas al pie
[1] Recordemos que la designación de orden proviene del prototipo de paso bajo por lo que aquí un filtro de paso de banda de segundo orden en realidad tiene dos resonadores, cada uno con una respuesta\(LC\) similar.