2.7: El método de las imágenes con cargas puntuales y esferas

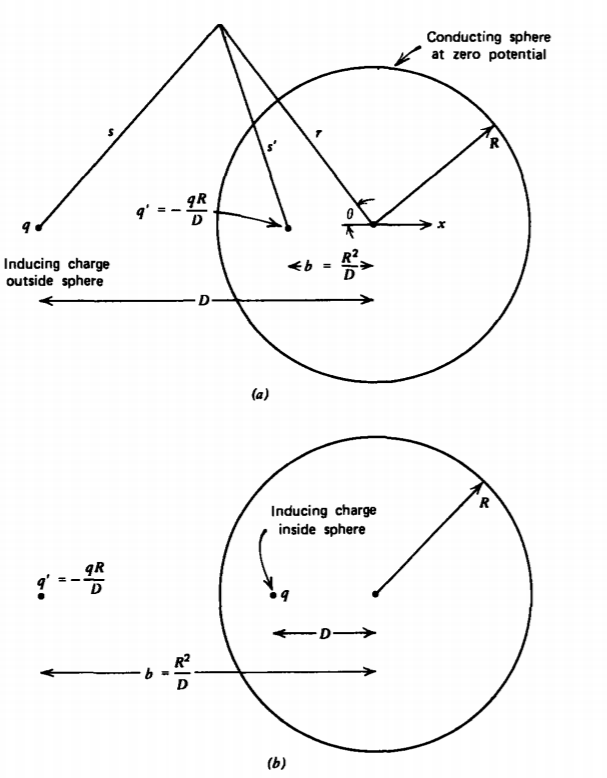
Carga puntual y esfera con conexión a tierra

Una carga puntual q es una distancia D desde el centro de la esfera conductora de radio R a potencial cero como se muestra en la Figura 2-27 a. Intentamos utilizar el método de imágenes colocando una sola carga de imagen q' a distancia b del centro de la esfera a lo largo de la línea que une el centro a la carga puntual q.

Necesitamos encontrar valores de q' y b que satisfagan la condición límite potencial cero a r = R. El potencial en cualquier punto P fuera de la esfera es

$$V= \frac{1}{4 \pi \varepsilon_{0}}(\frac{q}{s} + {q'}{s'}) \nonumber$$

donde la distancia de P a los cargos puntuales se obtienen de la ley de cosenos:

$$s = [r^{2} + D^{2} - 2rD \cos \theta]^{1/2} \\ s' = [b^{2} + r^{2} - 2rb \cos \theta]^{1/2} \nonumber$$

Figura 2-27 (a) El campo debido a una carga puntual q, una distancia D fuera de una esfera conductora de radio R, se puede encontrar colocando una sola carga de imagen - qR/D a una$b = R^{2}/D$ distancia del centro de la esfera. (b) Las mismas relaciones se mantienen verdaderas si la carga q está dentro de la esfera pero ahora la carga de imagen está fuera de la esfera, ya que D < R.

A r = R, el potencial en (1) debe ser cero de manera que q y q' deben ser de polaridad opuesta:

$$(\frac{q}{s} + \frac{q'}{s'})_{\vert_{r = R}} = 0 \Rightarrow (\frac{q}{s})^{2} + (\frac{q'}{s'})^{2}_{\vert_{r = R}} \nonumber$$

donde cuadramos las igualdades en (3) para eliminar las raíces cuadradas al sustituir (2),

$$q^{2}[b^{2} + R^{2} - 2Rb \cos \theta] = q'^{2}[R^{2} + D^{2} - 2RD \cos \theta] \nonumber$$

Dado que (4) debe ser cierto para todos los valores de$\theta$, obtenemos las siguientes dos igualdades:

$$q^{2}(b^{2} + R^{2}) = q'^{2}(R^{2} + D^{2}) \\ q^{2}b = q'^{2}D \nonumber$$

Al eliminar q y q' se obtiene una ecuación cuadrática en b:

$$b^{2} - bD[1 + (\frac{R}{D})^{2}] + R^{2} = 0 \nonumber$$

con solución

$$b = \frac{D}{2} [1 + (\frac{R}{D})^{2}] \pm \sqrt{\left \{ \begin{matrix} \frac{D}{2}[1 + (\frac{R}{D})^{2}] \end{matrix} \right \}^{2} - R^{2}} \\ = \frac{D}{2} [1 + (\frac{R}{D})^{2}] \pm \sqrt{\left \{ \begin{matrix} \frac{D}{2}[1 - (\frac{R}{D})^{2}] \end{matrix} \right \}^{2}} \\ = \frac{D}{2} \left \{ \begin{matrix} [1 + (\frac{R}{D})^{2}] \pm [1 - (\frac{R}{D})^{2}] \end{matrix} \right \} \nonumber$$

Tomamos la raíz negativa inferior para que la carga de imagen esté dentro de la esfera con valor obtenido al usar (7) en (5):

$$b = \frac{R^{2}}{D}, \: \: \: \: q'= -q \frac{R}{D} \nonumber$$

recordando de (3) que q y q' tienen signo opuesto. Ignoramos la solución b = D con q' = -q ya que el cargo de imagen siempre debe estar fuera de la región de interés. Si permitimos esta solución, la carga neta en la posición de la carga inductora es cero, contrariamente a nuestra afirmación de que la carga neta es q.

La distancia de carga de imagen b obedece a una relación similar a la encontrada para cargas de línea y cilindros en la Sección 2.6.3. Ahora, sin embargo, la magnitud de carga de imagen no es igual a la magnitud de la carga inductora porque no todas las líneas de fuerza terminan en la esfera. Algunas de las líneas de campo que emanan de q van alrededor de la esfera y terminan en el infinito.

La fuerza en la esfera conectada a tierra es entonces solo la fuerza sobre la carga de imagen -q' debido al campo de q:

$$f_{x} = \frac{qq'}{4 \pi \varepsilon_{0}(D-b)^{2}} = - \frac{q^{2}R}{4 \pi \varepsilon_{0}D(D-b)^{2}} = - \frac{q^{2}RD}{4 \pi \varepsilon_{0}(D^{2}-R^{2})^{2}} \nonumber$$

El campo eléctrico fuera de la esfera se encuentra desde (1) usando (2) como

$$\textbf{E} = - \nabla V = \frac{1}{4 \pi \varepsilon_{0}} (\frac{q}{s^{3}} [ (r-D \cos \theta) \textbf{i}_{r} + D \sin \theta \textbf{i}_{\theta}] \\ + \frac{q'}{s'^{3}} [ (r-b) \cos \theta) \textbf{i}_{r} + b \sin \theta \textbf{i}_{\theta}]) \nonumber$$

En la esfera donde$s' = (R/D)s$, la distribución de carga superficial se encuentra a partir de la discontinuidad en el campo eléctrico normal como se indica en la Sección 2.4.6:

$$\sigma (r=R) = \varepsilon_{0}E_{r}(r=R) = - \frac{q (D^{2} - R^{2})}{4 \pi R [ R^{2} + D^{2} - 2RD \cos \theta]^{3/2}} \nonumber$$

La carga total en la esfera

$$q_{T} = \int_{0}^{\pi} \sigma(r = R) 2 \pi R^{2} \sin \theta d \theta \\ = - \frac{q}{2}R(D^{2} - R^{2}) \int_{0}^{\pi} \frac{\sin \theta d \theta }{[R^{2} + D^{2} - 2RD - \cos \theta]^{3/2}} \nonumber$$

se puede evaluar introduciendo el cambio de variable

$$u = R^{2} + D^{2} - 2RD \cos \theta, \: \: \: du = 2 RD \sin \theta d \theta \nonumber$$

para que (12) se integre a

$$q_{T} = - \frac{q (D^{2}-R^{2})}{4D} \int-{(D-R)^{2}}^{(D+R)^{2}} \frac{du}{u^{3/2}} = - \frac{q(D^{2}-R^{2})}{4D} (-\frac{2}{u^{1/2}}) \bigg|_{(D-R)^{2}}^{(D+R)^{2}} = - \frac{qR}{D} \nonumber$$

que solo equivale a la carga de imagen q'.

Si la carga puntual q está dentro de la esfera puesta a tierra, la carga de imagen y su posición siguen siendo dadas por (8), como se ilustra en la Figura 2-27b. Desde D < R, la carga de imagen está ahora fuera de la esfera.

Carga puntual cerca de un plano conectado a tierra

Si la carga puntual es una distancia a de un plano puesto a tierra, como en la Figura 2-28 a, consideramos que el plano es una esfera de radio infinito R de manera que D = R + a. En el límite a medida que R se vuelve infinito, (8) se convierte

$$\lim_{R \rightarrow \infty \\ D = R + a} q' = -q, \: \: \: b = \frac{R}{(1 + a/R)} = R-a \nonumber$$

Figura 2-28 (a) Una carga puntual q cerca de un plano conductor tiene su carga de imagen -q simétricamente ubicada detrás del plano. b) Un campo eléctrico uniforme aplicado provoca una distribución uniforme de la carga superficial en el plano conductor. Cualquier carga inyectada debe superar la fuerza restauradora debido a su imagen para dejar el electrodo.

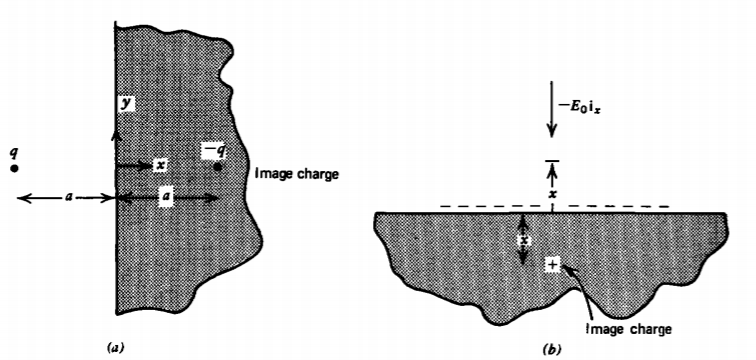
de manera que la carga de imagen es de igual magnitud pero polaridad opuesta y simétricamente ubicada en el lado opuesto del plano.

El potencial en cualquier punto (x, y, z) fuera del conductor se da en coordenadas cartesianas como

$$V = \frac{Q}{4 \pi \varepsilon_{0}}(\frac{1}{[(x + a)^{2} + y^{2} + z^{2}]^{1/2}} - \frac{1}{[(x-a)^{2} + y^{2}+ z^{2}]^{1/2}}) \nonumber$$

con campo eléctrico asociado

$$\textbf{E} = - \nabla V = \frac{q}{4 \pi \varepsilon_{0}} ( \frac{(x + a)\textbf{i}_{x} + y \textbf{i}_{y} + z \textbf{i}_{z}}{[(x+a)^{2} + y^{2} + z^{2}]^{3/2}} - \frac{(x-a) \textbf{i}_{x} + y \textbf{i}_{y} + z \textbf{i}_{z}}{[(x-a)^{2} + y^{2} + z^{2}]^{3/2}}) \nonumber$$

Tenga en cuenta que, según sea necesario, el campo es puramente normal al plano conectado a tierra

$$E_{y} (x=0) = 0, \: \: \: E_{z} (x=0) = 0 \nonumber$$

La densidad de carga superficial en el conductor viene dada por la discontinuidad de E normal:

$$\sigma(x = 0) = - \varepsilon_{0}E_{x}(x = 0) \\ = - \frac{q}{4\pi} \frac{2a}{[y^{2} + z^{2} + a^{2}]^{3/2}} \\ = - \frac{qa}{2 \pi (\textrm{r}^{2} + a^{2})^{3/2}} ; \textrm{r}^{2} = y^{2} + z^{2} \nonumber$$

donde surge el signo menos porque la superficie normal apunta en la dirección x negativa.

La carga total sobre la superficie conductora se obtiene integrando (19) sobre toda la superficie:

$$q_{T} = \int_{0}^{\infty} \sigma (x = 0 )2 \pi \textrm{r} d \textrm{r} \\ = - qa \int_{0}^{\infty} \frac{\textrm{r} d \textrm{r}}{(\textrm{r}^{2} + a^{2})^{3/2}} \\ = \frac{qa}{(\textrm{r}^{2} + a^{2})^{1/2}} \bigg|_{0}^{\infty} = -q \nonumber$$

Como siempre es el caso, la carga total sobre una superficie conductora debe ser igual a la carga de imagen.

La fuerza sobre el conductor se debe entonces solo al campo de la carga de imagen:

$$\textbf{f} = - \frac{q^{2}}{16 \pi \varepsilon_{0}a^{2}} \textbf{i}_{x} \nonumber$$

Esta fuerza de atracción evita que las cargas se escapen de la superficie de un electrodo cuando se aplica un campo eléctrico. Supongamos que un campo eléctrico$-E_{0} \textbf{i}_{x}$. se aplica perpendicular al electrodo mostrado en la Figura (2-28 b). Una distribución uniforme de carga superficial negativa$\sigma = - \varepsilon_{0}E_{0}$ como se indica en (2.4.6) surge para terminar el campo eléctrico ya que no hay campo eléctrico dentro del conductor. Entonces hay una fuerza coulómbica ascendente en la carga superficial, entonces ¿por qué no se sacan los electrones del electrodo? Imagine una carga expulsada -q a una distancia x del conductor. De (15) sabemos que una carga de imagen +q aparece entonces en -x que tiende a tirar de la carga - q de vuelta al electrodo con una fuerza dada por (21) con a = x en oposición al campo impuesto que tiende a tirar de la carga lejos del electrodo . La fuerza total sobre la carga - q es entonces

$$f_{x} = qE_{0} - \frac{q^{2}}{4 \pi \varepsilon_{0}(2x)^{2}} \nonumber$$

La fuerza es cero en la posición x _c

$$f_{x} = 0 \Rightarrow x_{c} = [\frac{q}{16 \pi \varepsilon_{0}E_{0}}]^{1/2} \nonumber$$

Para un electrón (q = 1.6 x 10 ^-19 culombios) en un campo de$E_{0} = 10^{6} v/m$,$x_{c} \approx 1.9 \times 10^{-8}$ m. Para valores menores de x la fuerza neta es negativa tendiendo a tirar de la carga de nuevo al electrodo. Si la carga puede ser impulsada más allá de x _c por fuerzas externas, el campo impuesto transportará entonces la carga lejos del electrodo. Si esta fuerza externa se debe al calentamiento del electrodo, el proceso se denomina emisión termiónica. La alta emisión de campo incluso con un electrodo frío ocurre cuando el campo eléctrico E _o se vuelve suficientemente grande (del orden de 10 ¹⁰ v/m) como para que la fuerza culómbica supere las fuerzas de unión mecánica cuántica que mantienen los electrones dentro del electrodo.

Esfera con carga constante

Si la carga puntual q está fuera de una esfera conductora (D > R) que ahora lleva una carga total constante Q ₀, la carga inducida sigue siendo$q' = -qR/D$. Dado que la carga total sobre la esfera es Q ₀, debemos encontrar otra carga de imagen que mantenga a la esfera una superficie equipotencial y tenga valor$Q_{0} + qR/D$. Esta otra carga de imagen debe colocarse en el centro de la esfera, como en la Figura 2-29a. La carga original q más la carga de imagen$q' = -qR/D$ pone la esfera a cero potencial. El cargo adicional de imagen en el centro de la esfera eleva el potencial de la esfera para

$$V = \frac{Q_{0} + qR/D}{4 \pi\varepsilon_{0}R} \nonumber$$

La fuerza sobre la esfera se debe ahora al campo de la carga puntual q que actúa sobre las dos cargas de imagen:

$$f_{x} = \frac{q}{4 \pi \varepsilon_{0}}(- \frac{qR}{D(D-b)^{2}} + \frac{(Q_{0} + qR/D)}{D^{2}}) = \frac{q}{4 \pi \varepsilon_{0}} (-\frac{qRD}{(D^{2}-R^{2})^{2}} + \frac{(Q_{0} + qR/D)}{D^{2}}) \nonumber$$

Figura 2-29 (a) Si una esfera conductora lleva una carga constante Q ₀ o (b) está a una tensión constante V ₀, se necesita una carga de imagen adicional en el centro de la esfera cuando una carga q está cerca.

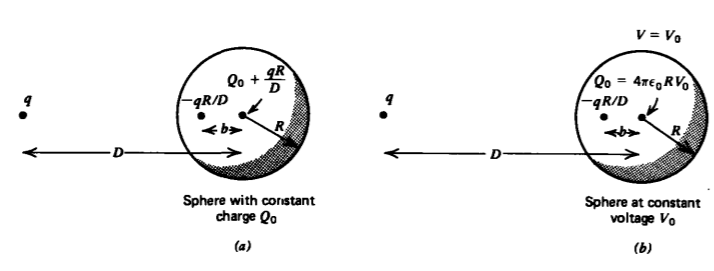
Esfera de Voltaje Constante

Si la esfera se mantiene a voltaje constante V ₀, la carga de imagen$q' = -qR/D$ a$b = R^{2}/D$ distancia del centro de la esfera aún mantiene la esfera a potencial cero. Para elevar el potencial de la esfera a V ₀, otra carga de imagen,

$$Q_{0} = 4 \pi \varepsilon_{0}RV_{0} \nonumber$$

deben colocarse en el centro de la esfera, como en la Figura 2-29 b. La fuerza sobre la esfera es entonces

$$f_{x} = \frac{q}{4 \pi \varepsilon_{0}} (-\frac{qR}{D(D-b)^{2}} + \frac{Q_{0}}{D^{2}}) \nonumber$$