5.3: Divergencia y Curl del Campo Magnético

Debido a nuestro éxito en el examen de diversas operaciones vectoriales en el campo eléctrico, vale la pena realizar operaciones similares en el campo magnético. Deberemos usar las siguientes identidades vectoriales de la Sección 1-5-4, Problema 1-24 y Secciones 2-4-1 y 2-4-2:

\[\nabla \cdot (\nabla \times \textbf{A}) = 0 \nonumber \]

\[\nabla \times (\nabla f) = 0 \nonumber \]

\[\nabla \bigg( \frac{1}{r_{QP}}) = - \frac{\textbf{i}_{QP}}{r^{2}_{QP}} \nonumber \]

\[\int_{V} \nabla^{2} \bigg( \frac{1}{r_{QP}} \bigg) d \textrm{V} = \left \{ \begin{matrix} 0, & r_{QP} \neq 0 \\ -4 \pi , & r_{QP} = 0 \end{matrix} \right. \nonumber \]

\[\nabla \cdot (\textbf{A} \times \textbf{B}) = \textbf{B} \cdot (\nabla \times \textbf{A}) - \textbf{A} \cdot \nabla \times \textbf{B} \nonumber \]

\[\nabla \times (\textbf{A} \times \textbf{B}) = (\textbf{B} \cdot \nabla)\textbf{A} - (\textbf{A} \cdot \nabla) \textbf{B} + (\nabla \cdot \textbf{B} \textbf{A} - (\nabla \cdot \textbf{A}) \textbf{B} \nonumber \]

\[\nabla (\textbf{A} \cdot \textbf{B}) = (\textbf{A} \cdot \nabla) \textbf{B} + (\textbf{B} \cdot \nabla) \textbf{A} + \textbf{A} \times (\nabla \times \textbf{B}) + \textbf{B} \times (\nabla \times \textbf{A}) \nonumber \]

5-3-1 Ley de Gauss para el Campo Magnético

Usando (3) el campo magnético debido a una distribución de volumen de la corriente J se reescribe como

\[\textbf{B} = \frac{\mu_{0}}{4 \pi} \int_{\textrm{V}} \frac{\textbf{J} \times \textbf{i}_{QP}}{r^{2}_{QP}} d \textrm{V} = \frac{-\mu_{0}}{4 \pi} \int_{\textrm{V}} \textbf{J} \times \nabla \bigg( \frac{1}{r_{QP}} \bigg) d \textrm{V} \nonumber \]

Si tomamos la divergencia del campo magnético con respecto a las coordenadas del campo, el operador del se puede llevar dentro de la integral ya que la integral está solo sobre las coordenadas de origen:

\[\nabla \cdot \textbf{B} = \frac{-\mu_{0}}{4 \pi} \int_{\textrm{V}} \nabla \cdot \bigg[ \textbf{J} \times \nabla \bigg( \frac{1}{r_{QP}} \bigg) \bigg] d \textrm{V} \nonumber \]

El integrando se puede ampliar usando (5)

\[\nabla \cdot \bigg[ \textbf{J} \times \nabla \bigg( \frac{1}{r_{QP}} \bigg) \bigg] = \nabla \bigg(\frac{1}{r_{QP}} \bigg) \cdot \underbrace{(\nabla \times \textbf{J})}_{0} - \textbf{J} \cdot \underbrace{\nabla \times \bigg[ \nabla \bigg( \frac{1}{r_{QP}} \bigg) \bigg]}_{0} = 0 \nonumber \]

El primer término en el lado derecho en (10) es cero porque J no es una función de coordenadas de campo, mientras que el segundo término es cero desde (2), el rizo del gradiente es siempre cero. Entonces (9) reduce a

\[\nabla \cdot \textbf{B} = 0 \nonumber \]

Esto contrasta con la ley de Gauss para el campo de desplazamiento donde el lado derecho es igual a la densidad de carga eléctrica. Como nadie ha descubierto aún ninguna carga magnética neta, no hay un término fuente en el lado derecho de (11).

El teorema de la divergencia nos da la representación integral equivalente

\[\int_{\textrm{V}} \nabla \cdot \textbf{B} d \textrm{V} = \oint_{S} \textbf{B} \cdot \textbf{B} \cdot \textbf{dS} = 0 \nonumber \]

lo que nos dice que el flujo magnético neto a través de una superficie cerrada es siempre cero. Tanto flujo entra en una superficie como la deja. Dado que no hay cargas magnéticas para terminar el campo magnético, las líneas de campo siempre están cerradas

5-3-2 Ley Circuital de Ampere

Del mismo modo tomamos el rizo de (8) para obtener

\[\nabla \times \textbf{B} = \frac{-\mu_{0}}{4 \pi} \int_{\textrm{V}} \nabla \times \bigg[ \textbf{J} \times \nabla \bigg( \frac{1}{r_{QP}} bigg) \bigg] d \textrm{V} \nonumber \]

donde nuevamente el operador del puede ser llevado dentro de la integral y solo opera en\(r_{QP}\)

Ampliamos el integrando usando (6):

\[\nabla \times \bigg[ \textbf{J} \times \nabla \bigg( \frac{1}{r_{QP}} \bigg) \bigg] = \bigg[ \nabla \bigg( \frac{1}{r_{QP}} \bigg) \underbrace{\cdot \bigg] \textbf{J}}_{0} - ( \textbf{J} \cdot \nabla) \nabla \bigg( \frac{1}{r_{QP}} \bigg) \\ + \bigg[ \nabla^{2} \bigg( \frac{1}{r_{QP}} \bigg) \bigg] \textbf{J} - \underbrace{(\nabla \cdot \textbf{J}) \nabla}_{0} \bigg(\frac{1}{r_{QP}}\bigg) \nonumber \]

donde dos términos en el lado derecho son cero porque J no es una función de las coordenadas del campo. Usando la identidad de (7)

\[\nabla \bigg[ \textbf{J} \cdot \nabla \bigg( \frac{1}{r_{QP}} \bigg) \bigg] = \bigg[ \nabla \bigg( \frac{1}{r_{QP}} \bigg) \underbrace{\cdot \nabla \bigg] \textbf{J}}_{0} + ( \textbf{J} \cdot \nabla ) \nabla \bigg(\frac{1}{r_{QP}}\bigg) \\ + \nabla \bigg( \frac{1}{r_{QP}} \bigg) \times \underbrace{(\nabla \times \textbf{J})}_{0} + \textbf{J} \times \bigg[ \underbrace{\nabla \times \nabla \bigg( \frac{1}{r_{QP}} \bigg)}_{0} \bigg] \nonumber \]

el segundo término en el lado derecho de (14) puede relacionarse con un gradiente puro de una cantidad porque los términos primero y tercero a la derecha de (15) son cero ya que J no es una función de coordenadas de campo. El último término en (15) es cero porque el rizo de un gradiente es siempre cero. Usando (14) y (15), (13) se puede reescribir como

\[\nabla \times \textbf{B} = \frac{\mu_{0}}{4 \pi} \int_{\textrm{V}} \{ \nabla \bigg[ \textbf{J} \cdot \nabla \bigg( \frac{1}{r_{QP}} \bigg) \bigg] - \textbf{K} \nabla^{2} \bigg( \frac{1}{r_{QP}} \bigg) \} d \textrm{V} \nonumber \]

Usando el teorema de gradiente, corolario del teorema de divergencia, (ver Problema 1-15a), la primera integral de volumen se convierte en una integral de superficie

\[\nabla \times \textbf{B} = \frac{\mu_{0}}{4 \pi} \bigg[ \int_{S} \underbrace{\textbf{J} \cdot \nabla \bigg( \frac{1}{r_{QP}} \bigg) \textbf{dS}}_{0} - \int_{\textrm{V}} \textbf{J} \nabla^{2} \bigg(\frac{1}{r_{QP}} \bigg) d \textrm{V} \bigg] \nonumber \]

Esta superficie rodea completamente la distribución de corriente de manera que S está afuera en una región de corriente cero donde J =0 para que la integral de la superficie sea cero. La integral de volumen restante es diferente de cero solo cuando\(r_{QP}\) =0, de modo que usando (4) finalmente obtenemos

\[\nabla \times \textbf{B} = \mu_{0} \textbf{J} \nonumber \]

que se conoce como ley de Ampere.

El teorema de Stokes aplicado a (18) resulta en la ley circuital de Ampere:

\[\int_{S} \nabla \times \frac{\textbf{B}}{\mu_{0}} \cdot \textbf{dS} = \oint_{L} \frac{\textbf{B}}{\mu_{0}} \cdot \textbf{dL} = \int_{S} \textbf{J} \cdot \textbf{dS} \nonumber \]

Al igual que la ley de Gauss, elegir el contorno correcto basado en argumentos de simetría a menudo permite soluciones fáciles para B.

Si tomamos la divergencia de ambos lados de (18), el lado izquierdo es cero porque la divergencia del rizo de un vector es siempre cero. Esto requiere que los sistemas de campo magnético tengan corrientes libres de divergencia para que la carga no pueda acumularse. Las corrientes siempre deben fluir en bucles cerrados.

5-3-3 Corrientes con simetría cilíndrica

Una corriente superficial\(K_{0} \textbf{i}_{z}\) fluye sobre la superficie de un cilindro hueco infinitamente largo de radio a. Considere los dos elementos de carga de línea ubicados simétricamente\(dI = K_{0} a d \phi\) y sus campos efectivos en un punto P en la Figura 5-11a. El campo magnético debido a ambos elementos actuales se cancela en la dirección radial pero se suma en la\(\phi\) dirección. El campo magnético total se puede encontrar haciendo una difícil integración sobre\(\phi\). Sin embargo

Figura 5-11 (a) El campo magnético de un cilindro infinitamente largo que transporta una corriente superficial paralela a su eje se puede encontrar utilizando la ley Biot-Savart para cada elemento de corriente de línea incremental. Los elementos ubicados simétricamente tienen componentes de campo radial que cancelan pero componentes de\(\phi\) campo que agregan. (b) Ahora que sabemos que el campo está puramente\(\phi\) dirigido, es más fácil utilizar la ley circuital de Ampere para un contorno circular concéntrico con el cilindro. Para r< a no pasa corriente por el contorno mientras que para r> a toda la corriente pasa por el contorno. (c) Si la corriente se distribuye uniformemente sobre el cilindro, el contorno más pequeño ahora encierra una fracción de la corriente.

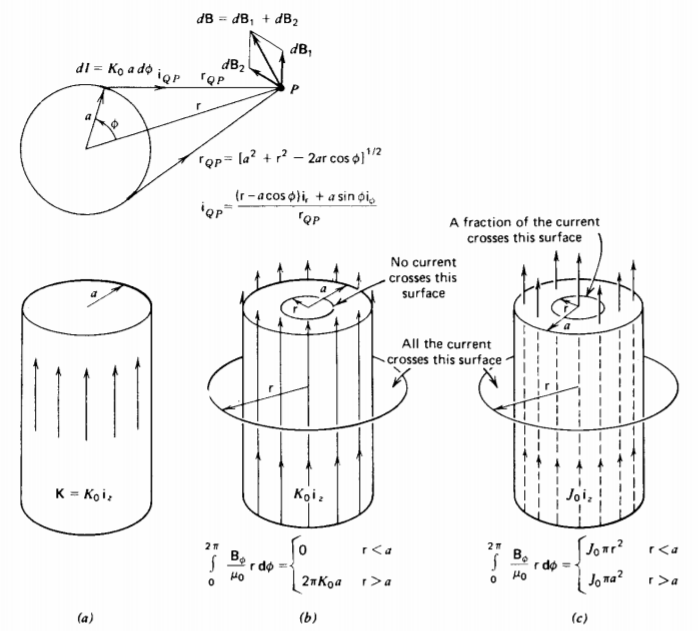
usar la ley circuital de Ampere de (19) es mucho más fácil. Como sabemos que el campo magnético está\(\phi\) dirigido y por simetría solo puede depender de r y no\(\phi\) o z, escogemos un contorno circular de radio constante r como en la Figura 5-11 b. ya que\(\textbf{dl} = r d \phi \textbf{i}_{\phi}\) está en la misma dirección que B, el producto puntual entre el campo magnético y dl se convierte en una multiplicación pura. Para r< a no pasa corriente a través de la superficie encerrada por el contorno, mientras que para r > a toda la corriente es puramente perpendicular a la normal a la superficie del contorno:

\[\oint_{L} \frac{\textbf{B}}{\mu_{0}} \cdot \textbf{dl} = \int_{0}^{2 \pi} \frac{B_{\phi}}{\mu_{0}} \textrm{r} d \phi = \frac{2 \pi \textrm{r} B_{\phi}}{\mu_{0}} = \left \{ \begin{matrix} K_{0} 2 \pi a = I, & \textrm{r} > a \\ 0, & \textrm{r} < a \end{matrix} \right. \nonumber \]

donde I es la corriente total en el cilindro.

El campo magnético es así

\[B_{\phi} = \left \{ \begin{matrix} \mu_{0} K_{0} a/r = \mu_{0} I/(2 \pi r), & r>a \\ 0, & r<a \end{matrix} \right. \nonumber \]

Fuera del cilindro, el campo magnético es el mismo que si toda la corriente se concentrara a lo largo del eje como una corriente de línea.

(b) Corriente de volumen

Si el cilindro tiene la corriente uniformemente distribuida sobre el volumen ya que\(J_{0} \textbf{i}_{z}\) el contorno que rodea a todo el cilindro todavía tiene la corriente total que\(I = J_{0} \pi a^{2}\) pasa a través de él. Si el contorno tiene un radio menor que el del cilindro, solo la fracción de corriente proporcional al área cerrada pasa a través de la superficie como se muestra en la Figura 5-11c:

\[\oint_{L} \frac{B_{\phi}}{\mu_{0}} \textrm{r} \d \phi = \frac{2 \pi \textrm{r} B_{\phi}}{\mu_{0}} = \left \{ \begin{matrix} J_{0} \pi a^{2} = I, & \textrm{r} >a \\ J_{0} \pi \textrm{r}^{2} = I \textrm{r}^{2}/a^{2}, & \textrm{r} < a \end{matrix} \right. \nonumber \]

para que el campo magnético sea

\[B_{\phi} = \left \{ \begin{matrix} \frac{\mu_{0} J_{0} a^{2}}{2 \textrm{r}} = \frac{\mu_{0}I}{2 \pi \textrm{r}}, & \textrm{r} > a \\ \frac{\mu_{0} J_{0} \textrm{r}}{2} = \frac{\mu_{0}I \textrm{r}}{2 \pi a^{2}}, & \textrm{r} < a \end{matrix} \right. \nonumber \]