5.4: El potencial vectorial

Singularidad

Como la divergencia del campo magnético es cero, podemos escribir el campo magnético como el rizo de un vector,

\[\nabla \cdot \textbf{B} = 0 \Rightarrow \textbf{B} = \nabla \times \textbf{A} \label{1} \]

donde A se llama potencial vectorial, ya que la divergencia del rizo de cualquier vector es siempre cero. A menudo es más fácil calcular A y luego obtener el campo magnético de la Ecuación\ ref {1}.

De la ley de Ampere, el potencial vectorial está relacionado con la densidad de corriente como

\[\nabla \times \textbf{B} = \nabla \times (\nabla \times \textbf{A}) = \nabla (\nabla \cdot \textbf{A}) - \nabla^{2} \textbf{A} = \mu_{0} \textbf{J} \nonumber \]

Vemos que (1) no define de manera única A, ya que podemos sumar el gradiente de cualquier término a A y no cambiar el valor del campo magnético, ya que el curl del gradiente de cualquier función es siempre cero:

\[\textbf{B} \rightarrow \textbf{A} + \nabla f \Rightarrow \textbf{B} = \nabla \times ( \textbf{A} + \nabla f ) = \nabla \times \textbf{A} \nonumber \]

El teorema de Helmholtz establece que para especificar de manera única un vector, se debe especificar tanto su curl como su divergencia y que lejos de las fuentes, los campos deben acercarse a cero. Para probar este teorema, digamos que nos dan, el rizo y divergencia de A y estamos para determinar qué es A. ¿Hay algún otro vector C, diferente de A que tenga el mismo rizo y divergencia? Intentamos C de la forma

\[\textbf{C} = \textbf{A} + \textbf{a} \nonumber \]

y vamos a demostrar que a es cero.

Por definición, el rizo de C debe ser igual al rizo de A de manera que el rizo de a debe ser cero:

\[\nabla \times \textbf{C} = \nabla \times (\textbf{A} + \textbf{a}) = \nabla \times \textbf{A} \Rightarrow \nabla \times \textbf{a} = 0 \nonumber \]

Esto requiere que a sea derivable del gradiente de una función escalar f

\[\nabla \times \textbf{a} = 0 \Rightarrow \textbf{a} = \nabla f \nonumber \]

De igual manera, la condición de divergencia requiere que la divergencia de a sea cero,

\[\nabla \cdot \textbf{C} = \nabla \cdot (\textbf{A} + \textbf{a}) = \nabla \cdot \textbf{A} \Rightarrow \nabla \cdot \textbf{a} = 0 \nonumber \]

de manera que el laplaciano de\(f\) debe ser cero,

\[\nabla \cdot \textbf{a} = \nabla^{2} f = 0 \nonumber \]

En el Capítulo 2 obtuvimos una ecuación y solución similar para el potencial eléctrico que va a cero lejos de la distribución de carga:

\[\nabla^{2} V = - \frac{\rho}{\varepsilon} \Rightarrow V = \int_{\textrm{V}} \frac{\rho d \textrm{V}}{4 \pi \varepsilon r_{QP}} \nonumber \]

Si equiparamos f a V, entonces\(\rho\) debe ser cero dándonos que la función escalar f también es cero. Es decir, la solución a la ecuación de Laplace de (8) para fuentes cero en todas partes es cero, a pesar de que la ecuación de Laplace en una región sí tiene soluciones distintas de cero si hay fuentes en otras regiones del espacio. Con f cero, de (6) tenemos que el vector a también es cero y luego C = A, demostrando así el teorema de Helmholtz.

5-4-2 El potencial vectorial de una distribución de corriente

Como somos libres de especificar la divergencia del potencial vectorial, tomamos el caso más simple y lo ponemos a cero:

\[\nabla \cdot \textbf{A} = 0 \nonumber \]

Entonces (2) reduce a

\[\nabla^{2} \textbf{A} = - \mu_{0} \textbf{J} \nonumber \]

Cada componente vectorial de (11) es solo la ecuación de Poisson para que la solución también sea análoga a (9)

\[\textbf{A} = \frac{\mu_{0}}{4 \pi} \int_{\textrm{V}} \frac{\textbf{J} d \textrm{V}}{r_{QP}} \nonumber \]

El potencial vectorial suele ser más fácil de usar ya que está en la misma dirección que la actual, y podemos evitar el producto cruzado a menudo complicado en la ley Biot-Savart. Para cargas de puntos móviles, así como para corrientes superficiales y de línea, utilizamos (12) con los elementos de corriente apropiados:

\[\textbf{J} d \textrm{V} \rightarrow \textbf{K} d \textrm{S} \rightarrow \textbf{I} dL \rightarrow q \textbf{v} \nonumber \]

5-4-3 El potencial vectorial y el flujo magnético

Usando el teorema de Stokes, el flujo magnético a través de una superficie se puede expresar en términos de una línea integral del potencial vectorial:

\[\begin{align*} \Phi &= \int_{S} \textbf{B} \cdot \textbf{dS} \\[4pt] &= \int_{S} \nabla \times \textbf{A} \cdot \textbf{dS} \\[4pt] &= \oint_{L} \textbf{A} \cdot \textbf{dl} \end{align*} \nonumber \]

(a) Corriente de línea de longitud finita

El problema de una corriente\(I\) de línea de longitud\(L\), como en la Figura 5-12a parece no ser físico ya que la corriente debe ser continua. Sin embargo, podemos imaginar que esta corriente de línea forma parte de un bucle cerrado y calculamos el potencial vectorial y el campo magnético a partir de esta parte del bucle.

Figura 5-12 (a) El campo magnético debido a una corriente de línea de longitud finita se encuentra más fácilmente utilizando el potencial vectorial, que está en la dirección de la corriente. Este problema es físico solo si se considera que la corriente de línea es parte de un bucle cerrado. (b) El campo magnético de una longitud\(w\) de corriente superficial se encuentra superponiendo el potencial vectorial de (a) con\(L \rightarrow \infty\). Las líneas de campo son líneas de constante\(A_{z}\) (c) El flujo magnético a través de un bucle de corriente cuadrado está en la dirección - x por la regla de la derecha.

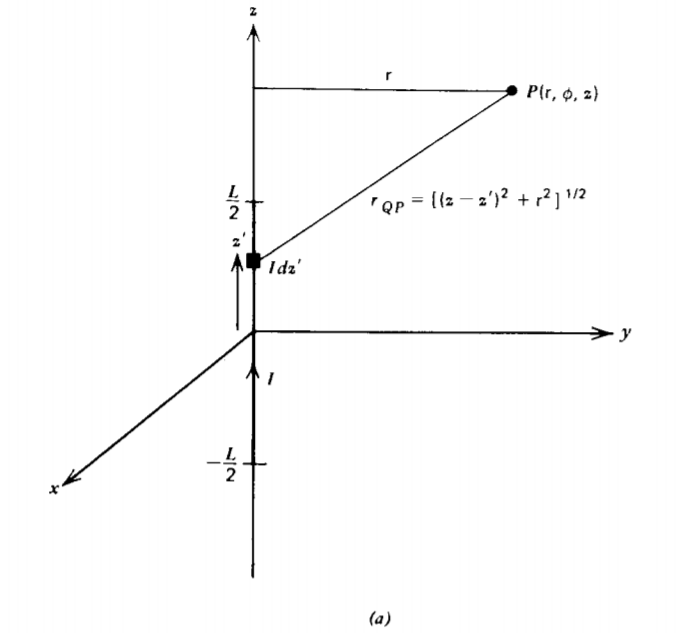
La distancia\(r_{QP}\) desde el elemento actual\(I \: dz'\) hasta el punto de campo en la coordenada (r,\(\phi\), z) es

\[r_{QP} = [ (z-z')^{2} + \textrm{r}^{2}]^{1/2} \nonumber \]

El potencial del vector es entonces

\[\begin{align*} A_{z} &= \frac{\mu_{0}I}{4 \pi} \int_{-L/2}^{L/2} \frac{dz'}{[(z-z')^{2} + \textrm{r}^{2}]^{1/2}} \\[4pt] &= \frac{\mu_{0}I}{4 \pi} \ln \left( \frac{-z + L/2 + [(z-L/2)^{2} + \textrm{r}^{2}]^{1/2}}{-(z+L/2) + [(z + L/2)^{2} + \textrm{r}^{2}]^{1/2}} \right) \\[4pt] &= \frac{\mu_{0}I}{4 \pi} \left(\sinh^{-1} \frac{-z + L/2}{\textrm{r}} + \sinh^{-1} \frac{z + L/2}{\textrm{r}} \right) \end{align*} \nonumber \]

con campo magnético asociado

\[ \begin{align*} \textbf{B} &= \nabla \times \textbf{A} \\[4pt] &= \left( \frac{1}{\textrm{r}} \frac{\partial A_{z}}{\partial \phi} - \frac{\partial A_{\phi}}{dz} \right) \textbf{i}_{\textrm{r}} + \left( \frac{\partial A_{\textrm{r}}}{\partial z} - \frac{\partial A_{z}}{\partial \textrm{r}} \right) \textbf{i}_{\phi} + \frac{1}{\textrm{r}} \left( \frac{\partial}{\partial \textrm{r}} (\textrm{r} A_{\phi}) - \frac{\partial A_{\textrm{r}}}{\partial \phi} \right) \textbf{i}_{z} \\[4pt] &= - \frac{\partial A_{z}}{\partial \textrm{r}} \textbf{i}_{\phi} \\[4pt] &= \frac{- \mu_{0} I \textrm{r}}{4 \pi} \left( \frac{1}{[(z-L/2)^{2} + \textrm{r}^{2}]^{1/2} ( -z + L/2 + [(z-L/2)^{2} + \textrm{r}^{2}]^{1/2} )} - \frac{1}{[(z+L/2)^{2} + \textrm{r}^{2}]^{1/2} (-(z-L/2) + [(z + L/2)^{2} + \textrm{r}^{2}]^{1/2} ) } \right) \textbf{i}_{\phi} \\[4pt] &= \frac{\mu_{0}I}{4 \pi \textrm{r}} \left( \frac{-z + L/2}{[\textrm{r}^{2} + (z-L/2)^{2}]^{1/2}} + \frac{z + L/2}{[\textrm{r}^{2} + (z + L/2)^{2}]^{1/2}} \right) \textbf{i}_{\phi} \end{align*} \nonumber \]

Figura 5-12

Para grandes\(L\), (17) se acerca al campo de una corriente de línea infinitamente larga como se indica en la Sección 5-2-2:

\[\lim_{L \rightarrow \infty} \left \{ \begin{matrix} A_{z} = \frac{- \mu_{0}I}{2 \pi} \ln \textrm{r} + \textrm{const} \\ B_{\phi} = - \frac{\partial A_{z}}{\partial \textrm{r}} = \frac{\mu_{0} I}{2 \pi \textrm{r}} \end{matrix} \right. \nonumber \]

Tenga en cuenta que la constante de potencial vectorial en (18) es infinita, pero esto no es importante ya que esta constante no tiene ninguna contribución al campo magnético.

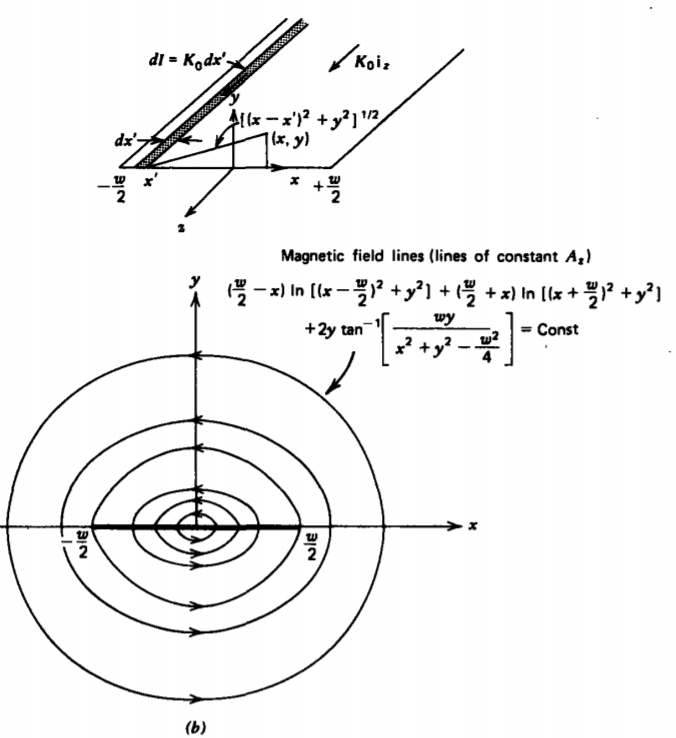
(b) Corriente de superficie de ancho finito

Si una corriente superficial\(K_{0} \text{i}_{z}\) de ancho\(w\), se forma colocando juntos muchos elementos de corriente de línea, como en la Figura 5-12b, el potencial vectorial en (x, y) desde el elemento de corriente de línea\(K_{0} dx'\) en la posición x' viene dado por (18):

\[dA_{z} = \frac{- \mu_{0} K_{0} dx'}{4 \pi} \ln [(x-x')^{2} + y^{2}] \nonumber \]

El potencial total del vector se encuentra integrando sobre todos los elementos:

\[A_{z} = \frac{-\mu_{0}K_{0}}{4 \pi} \int_{-w/2}^{+w/2} \ln [(x-x')^{2} + y^{2}]dx' \\ = \frac{-\mu_{0}K_{0}}{4 \pi} \left( (x'-x) \ln [(x-x')^{2} + y^{2}]-2(x'-x) \\ = 2y \tan^{-1} \frac{(x'-x)}{y}\right) \bigg|_{-w/2}^{+w/2} \\ = \frac{-\mu_{0}K_{0}}{4 \pi} \left( \left( \frac{w}{2} - x \right) \ln \bigg[ \left( x - \frac{w}{2} \right)^{2} + y^{2} \bigg] \\ + \left( \frac{w}{2} + x \right) \ln \bigg[ \left( x + \frac{w}{2} \right)^{2} + y^{2} \bigg] \\ -2 w + 2 y \tan^{-1} \frac{wy}{y^{2} +x^{2} - w^{2}/4} \right) \nonumber \]

*

El campo magnético es entonces

\[\textbf{B} = \textbf{i}_{x} \frac{\partial A_{z}}{\partial y} - \textbf{i}_{y} \frac{\partial A_{z}}{\partial x} \\ = \frac{- \mu_{0} K_{0}}{4 \pi} \left( 2 \tan^{-1} \frac{wy}{y^{2} + x^{2} - w^{2}/4} \textbf{i}_{x} + \ln \frac{(x + w/2)^{2} + y^{2}}{(x - w/2)^{2} + y^{2}} \textbf{i}_{y} \right) \nonumber \]

El potencial vectorial en geometrías bidimensionales también es útil para trazar líneas de campo,

\[\frac{dy}{dx} = \frac{B_{y}}{B_{x}} = \frac{- \partial A_{z}/ \partial x}{\partial A_{z} / \partial y} \nonumber \]

porque si cruzamos multiplicar (22),

\[\frac{\partial A_{z}}{\partial x} dx + \frac{\partial A_{z}}{\partial y} dy = d A_{z} = 0 \Rightarrow A_{z} = \textrm{const} \nonumber \]

vemos que es constante en una línea de campo. Las líneas de campo en la Figura 5-12b son solo líneas de constante\(A_{z}\). El potencial vectorial juega así el mismo papel que la función de corriente eléctrica en las Secciones 4.3.2b y 4.4.3b.

\[\tan^{-1} (a-b) + \tan^{-1} (a + b) = \tan ^{-1} \frac{2a}{1-a^{2} + b^{2}} \nonumber \]

(c) Flujo a través de un bucle cuadrado

El potencial vectorial para el bucle cuadrado en la Figura 5-12c con un radio muy pequeño a se encuentra superponiendo (16) para cada lado con cada componente de A en la misma dirección que la corriente en cada tramo. El campo magnético resultante viene dado entonces por cuatro términos como el de (17) para que el flujo pueda calcularse directamente integrando el componente normal de B sobre el área del bucle. Este método es sencillo pero el álgebra es engorroso

Un método más fácil es usar (14) ya que ya conocemos el potencial vectorial a lo largo de cada pata. Escogemos un contorno que se extiende a lo largo del límite interior del cable en un radio pequeño a. Como cada pierna es idéntica, solo tenemos que integrar sobre una pierna, luego multiplicar el resultado por 4:

\[\begin{align*} \Phi &= 4 \int_{a-D/2}^{-a + D/2} A_{z} \\[4pt] &= \frac{\mu_{0}I}{\pi} \int_{a-D/2}^{-a + D/2} ( \sinh^{-1} \frac{-z + D/2}{a} + \sinh^{-1} \frac{z + D/2}{a} \right) dz \\[4pt] &= \frac{\mu_{0}I}{\pi} \bigg[ - \left( \frac{D}{2} - z) \sinh ^{-1} \frac{-z + D/2}{a} + \bigg[ \left( \frac{D}{2} - z \right)^{2} + a^{2} \bigg]^{1/2} + \left(\frac{D}{2} + z \right) \sinh^{-1} \frac{z + D/2}{a} - \bigg[ \left( \frac{D}{2} + z \right)^{2} + a^{2} \bigg]^{1/2} \bigg] \bigg|_{a-D/2}^{-a + D/2} \\[4pt] &= 2 \frac{\mu_{0} I}{\pi} \left( - a \sinh^{-1} 1 + a \sqrt{2} + (D-a) \sinh^{-1} \frac{D-a}{a} -[(D-a)^{2} + a^{2}]^{1/2} \right) \end{align*} \nonumber \]

A medida que\(a\) se vuelve muy pequeño, (24) se reduce a

\[\lim_{a \rightarrow 0} \Phi = 2 \frac{\mu_{0}I}{\pi} D \left( \sinh^{-1} \left( \frac{D}{a} \right) - 1 \right) \nonumber \]

Vemos que el flujo a través del bucle es proporcional a la corriente. Esta constante de proporcionalidad se llama autoinductancia y es solo una función de la geometría:

\[L = \frac{\Phi}{I} = 2 \frac{\mu_{0}D}{\pi} \left( \sinh^{-1} \left( \frac{D}{a} \right) - 1 \right) \nonumber \]

La inductancia está más desarrollada en el Capítulo 6.