5.6: Condiciones de contorno
( \newcommand{\kernel}{\mathrm{null}\,}\)
En los límites interfaciales que separan materiales de diferentes propiedades, los campos magnéticos a cada lado del límite deben obedecer ciertas condiciones. El procedimiento consiste en utilizar la forma integral de las leyes de campo para contornos, superficies y volúmenes de tamaños diferenciales de la misma manera que se realizó para campos eléctricos en la Sección 3-3.
Para resumir nuestro desarrollo hasta ahora, las leyes de campo para campos magnéticos en forma diferencial e integral son
∇×H=Jf,∮LH⋅dl=∫SJf⋅dS
∇×M=Jm,∮LM⋅dl=∫SJm⋅dS
∇⋅B=0,∮SB⋅dS=0
5-6-1 Componente tangencial de H
Aplicamos la ley circuital de Ampere de (1) al contorno de tamaño diferencial que encierra la interfaz, como se muestra en la Figura 5-22a. Debido a que se supone que la interfaz es infinitamente delgada, los lados cortos etiquetados c y d son de longitud cero y así ofrecen
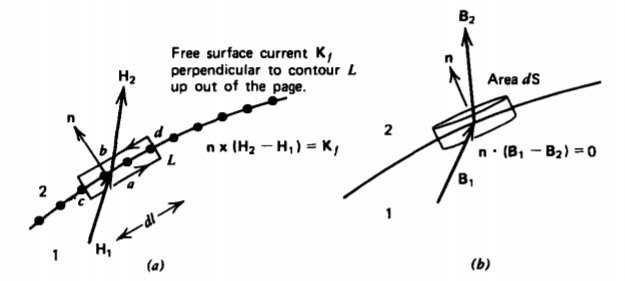
sin contribución a la línea integral. Los dos lados restantes rinden
∮LH⋅dl=(H1t−H2t)dl=Kfndl
dondeKfn. es el componente de la corriente de superficie libre perpendicular al contorno por la regla de la derecha en este caso hacia arriba de la página. Por lo tanto, el componente tangencial del campo magnético puede ser discontinuo por una corriente de superficie libre,
(H1t−H2t)=Kfn⇒n×(H2−H1)=Kf
donde la unidad normal apunta desde la región 1 hacia la región 2. Si no hay corriente superficial, el componente tangencial de H es continuo.
5-6-2 Componente tangencial de M
La ecuación (2) es de la misma forma que (6) por lo que podemos usar los resultados de (5) reemplazar H por M y K f por K m la corriente de magnetización superficial:
(M1t−M2t)=Kmn,n×(M2−M1)=Km
Esta condición límite confirma el resultado para la corriente de magnetización superficial encontrada en el Ejemplo 5-1.
5-6-3 Componente Normal de B
La figura 5-22b muestra un pequeño volumen cuyas superficies superior e inferior son paralelas y están a ambos lados de la interfaz. El lado cilíndrico corto, al ser de longitud cero, no ofrece ninguna contribución a (3), lo que reduce así a
∮SB⋅dS=(B2n−B1n)dS=0
produciendo la condición límite de que el componente de B normal a una interfaz de discontinuidad es siempre continuo:
B1n−B2n=0⇒n⋅(B1−B2)=0
Una losa de extensión infinita en las direcciones x e y se coloca dentro de un campo magnético uniformeH0iz como se muestra en la Figura 5-23.
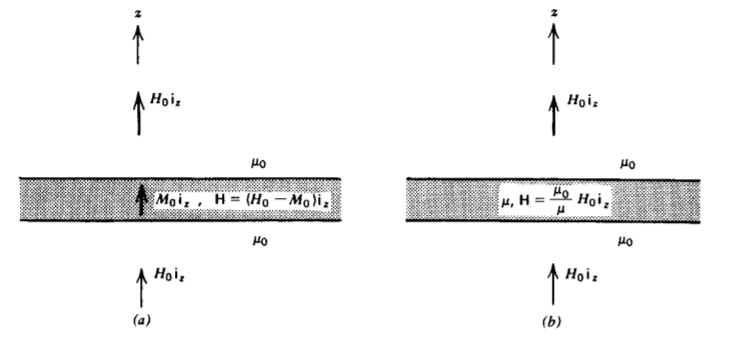
Encuentra el campo H dentro de la losa cuando está
(a) magnetizada permanentemente con magnetizaciónM0iz
(b) un material permeable lineal con permeabilidadμ.
Solución
Para ambos casos, (8) requiere que el campo B a través de los límites sea continuo ya que normalmente es incidente.
a) Para la losa permanentemente magnetizada, esto requiere que
μ0H0=μ0(H+M0)⇒H=H0−M0
Tenga en cuenta que cuando no hay campo aplicado externamente (H0= 0), el campo resultante dentro de la losa se dirige opositamente a la magnetización de manera que B = 0.
(b) Para un medio permeable lineal (8) se requiere
μ0H0=μH⇒H=μ0μH0
Paraμ>μ0 el campo magnético interno se reduce. SiH0 se establece en cero, el campo magnético dentro de la losa también es cero.


