2.3. Curvas definidas implícitamente en el espacio
- Page ID
- 49612
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vector}[1]{\vec{\mathbf{#1}}}\)
\( \newcommand{\Disco}{\Bbb D}\)
\( \newcommand{\C}{\Bbb C}\)
\( \newcommand{\Q}{\Bbb Q}\)
\( \newcommand{\R}{\Bbb R}\)
\( \newcommand{\K}{\Bbb K}\)
\( \newcommand{\N}{\Bbb N}\)
\( \newcommand{\Z}{\Bbb Z}\)
\( \newcommand{\bo}{\textbf O}\)
\( \newcommand{\eps}{\varepsilon}\)
\( \newcommand{\la}{\lambda}\)
\( \newcommand{\om}{\omega}\)
\( \newcommand{\bmatriz}{\bmatrix \format \r&&\quad\r\\}\)
\( \newcommand{\bmatrize}{\bmatrix \format \c&&\quad\c\\}\)
\( \newcommand{\sep}{\, \equiv \,}\)
\( \newcommand{\xsep}{\quad \equiv \quad}\)
\( \newcommand{\xlsep}{\qquad \equiv \qquad}\)
\( \newcommand{\matriz}{\bmatrix\format\r&&\quad\r\\}\)
\( \newcommand{\endmatriz}{\endbmatrix}\)
\( \newcommand{\conj}[1]{\overline{}[1]}}\)
\( \newcommand{\vector}[1]{\vec{\textbf {}[1]}}}\)
\( \newcommand{\abs}[1]{\left\vert {#1} \right\vert}}\)
\( \newcommand{\norm}[1]{\left\Vert {#1}\right\Vert}\)
\( \newcommand{\bil}[2]{\left\langle {#1},{#2} \right\rangle}\)
\( \newcommand{\absbil}[2]{\abs{ \bil{#1}{#2} }}\)
\( \newcommand{\vectori}{\vector{\mathbf{\i}}}\)
\( \newcommand{\vectorj}{\vector{\mathbf{\j}}}\)
\( \newcommand{\vectork}{\vector{\mathbf{k}})\)
\( \newcommand{\vectorr}{\vector r}\)
\( \newcommand{\vectorrp}{\vector r}\,{}'}\)
\( \newcommand{\vectorrs}{\vector r}\,{}''}\)
\( \newcommand{\parteim}{\mathop{\text{Im}}\nolimits}\)
\( \newcommand{\partere}{\mathop{\text{Re}}\nolimits}\)
\( \newcommand{\sen}{\mathop{\text{sen}}\nolimits}\)
\( \newcommand{\sinc}{\mathop{\text{sinc}}\nolimits}\)
\( \newcommand{\sa}{\mathop{\text{sa}}\nolimits}\)
\( \newcommand{\senh}{\mathop{\text{senh}}\nolimits}\)
\( \newcommand{\arsenh}{\mathop{\text{arsenh}}\nolimits}\)
\( \newcommand{\arcosh}{\mathop{\text{arcosh}}\nolimits}\)
\( \newcommand{\Log}{\mathop{\text{Log}}\nolimits}\)
\( \newcommand{\Ln}{\mathop{\text{Ln}}\nolimits}\)
\( \newcommand{\Arg}{\mathop{\text{Arg}}\nolimits}\)
\( \newcommand{\arcsen}{\mathop{\text{arcsen}}\nolimits}\)
\( \newcommand{\arcos}{\mathop{\text{arccos}}\nolimits}\)
\( \newcommand{\arctg}{\mathop{\text{arctg}}\nolimits}\)
\( \newcommand{\ran}{\mathop{\text{ran}}\nolimits}\)
\( \newcommand{\maxe}{\mathop{\text{máx}}}\)
\( \newcommand{\mine}{\mathop{\text{mín}}}\)
\( \newcommand{\lime}{\mathop{\text{lím}}}\)
\( \newcommand{\lin}{\mathop{\text{lin}}\nolimits}\)
\( \newcommand{\inte}{\mathop{\text{int}}\nolimits}\)
\( \newcommand{\grad}{\mathop{\text{grad}}\nolimits}\)
\( \newcommand{\signo}{\mathop{\text{sig}}\nolimits}\)
\( \newcommand{\fl}{\mathop{\text{flot}}\nolimits}\)
\( \newcommand{\essup}{\mathop{\text{ess}\,\text{sup}}\nolimits}\)
\( \newcommand{\card}{\mathop{\text{card}}\nolimits}\)
\( \newcommand{\rot}{\mathop{\text{rot}}\nolimits}\)
\( \newcommand{\diver}{\mathop{\text{div}}\nolimits}\)
\( \newcommand{\volum}{\mathop{\text{vol}}\nolimits}\)
\( \newcommand{\Res}{\mathop{\text{Res}}\nolimits}\)
\( \newcommand{\grado}{\mathop{\text{gr}}\nolimits}\)
\( \newcommand{\dpar}[2]{\dfrac{\partial{#1}}{\partial{#2}}}\)
\( \newcommand{\dparx}[1]{\dfrac{\partial {#1}}{\partial x}}}\)
\( \newcommand{\dpary}[1]{\dfrac{\partial {#1}}{\partial y}}}\)
\( \newcommand{\dparz}[1]{\dfrac{\partial {#1}}{\partial z}}}\)
\( \newcommand{\dparr}[1]{\dfrac{\partial {#1}}{\partial r}}}\)
\( \newcommand{\dparth}[1]{\dfrac{\partial {#1}}{\partial \theta}}}\)
\( \newcommand{\dparxx}[1]{\dfrac{\partial^2 {#1}}{\partial x^2}}}\)
\( \newcommand{\dparyy}[1]{\dfrac{\partial^2 {#1}}{\partial y^2}}}\)
\( \newcommand{\dparxy}[1]{\dfrac{\partial^2 {#1}}{\partial x \partial y}}}\)
\( \newcommand{\dparzz}[1]{\dfrac{\partial^2 {#1}}{\partial z^2}}}\)
\( \newcommand{\dparxz}[1]{\dfrac{\partial^2 {#1}}{\partial x \partial z}}}\)
\( \newcommand{\dparyz}[1]{\dfrac{\partial^2 {#1}}{\partial y \partial z}}}\)
\( \newcommand{\dpardos}[2]{\dfrac{\partial^2 {#1}}{\partial {#2}^2}}}\)
\( \newcommand{\dparcruz}[3]{\dfrac{\partial^2 {#1}}{\partial {#2} \partial {#3}}}\)
\( \newcommand{\dtan}[1]{ \dfrac{\partial {#1}}{\partial {\vector t}} }}\)
\( \newcommand{\dnormal}[1]{ \dfrac{\partial {#1}}{\partial {\vector n}} }}\)
Curvas dadas por la intersección de dos superficies
Dados dos campos escalares \( F(x,y,z) \) y \( G(x,y,z) \), los puntos \( (x,y,z) \) que cumplen \( F(x,y,z)=0 \) y \( G(x,y,z)=0 \) forman, en general, una curva \( C \) en el espacio tridimensional. Entonces se dice que estas ecuaciones definen implícitamente la curva \( C \) y se llaman ecuaciones implícitas de \( C \). El ejemplo más simple es la definición de una recta como intersección de dos planos. Otro ejemplo son las cónicas, definidas en 3D como la intersección de un cono y un plano, o las curvas dadas por la intersección de dos cuádricas, como la curva de Viviani, que es la curva en forma de \( 8 \) dada por la intersección de la esfera \( x^2+y^2+z^2=1 \) con el cilindro circular \( x^2+y^2=x \), en otras palabras, es el conjunto de puntos cuyas coordenadas \( (x,y,z) \) son las soluciones de las ecuaciones \(F(x,y,z) = x^2+y^2+z^2-1=0 \) y \( G(x,y,z)=x^2+y^2-x=0 \).
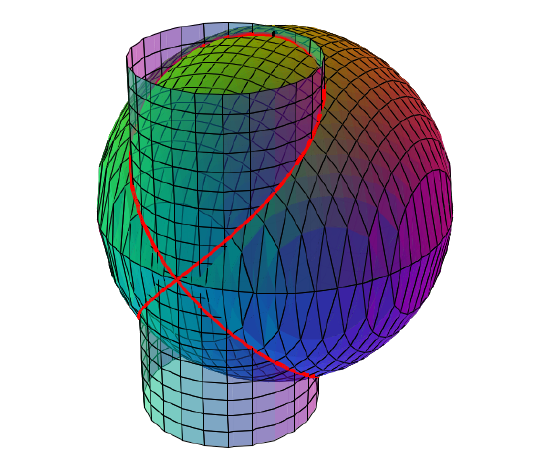
La curva de Viviani.
Recta tangente a una curva dada por la intersección de dos superficies. Para ver que el conjunto \( C \) de los puntos \( (x,y,z) \) que cumplen \( F(x,y,z)=0 \) y \( G(x,y,z)=0 \) es una curva, lo ideal sería despejar dos de las variables en función de la tercera, que podría usarse como parámetro de la curva. Si \( C \) es una curva, entonces está contenida en ambas superficies, luego que el vector tangente a \( C \) en un punto \( P \) debe ser ortogonal tanto a \( \nabla F(P) \) como a \( \nabla G(P) \). En consecuencia, el producto vectorial \( \nabla F(P)\times \nabla G(P) \) es, si no es el vector nulo, tangente a la curva en \( P \), luego la condición debe ser que \( \nabla F(P) \) y \( \nabla G(P) \) sean linealmente independientes para que \( \nabla F(P)\times \nabla G(P) \neq \vecs 0 \).
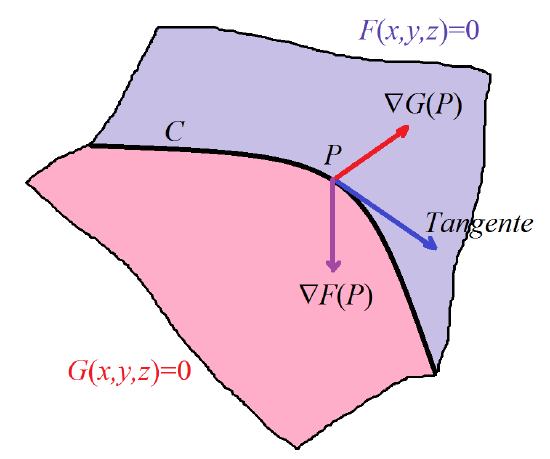
Curva dada por ecuaciones implícitas.
Teorema de la función implícita para una curva en el espacio o para dos ecuaciones con tres variables.
Teorema de la función implícita (3D, dos ecuaciones). Sean \( F \) y \( G \) funciones de clase \( C^n(U) \) y \( P=(x_0,y_0,z_0) \) un punto interior del dominio \( U \) tal que \( F(P)=0 \) y \( G(P)=0 \). Si los vectores gradientes \( \nabla F(P) \) y \( \nabla G(P) \) son linealmente independientes, entonces cerca del punto \( P \) los puntos \( (x,y,z) \) que cumplen \( F(x,y,z)=0 \) y \( G(x,y,z)=0 \) forman una curva \( C \) que podemos parametrizar usando una de las variables como parámetro.
Concretamente, si \( \nabla F(P) \) y \( \nabla G(P) \) son linealmente independientes, entonces \( \nabla F(P)\times \nabla G(P)\neq \vecs 0 \) y podemos usar como parámetro de la curva cualquiera de las variables cuya coordenada correspondiente en \( \nabla F(P) \times \nabla G(P) \) no sea cero. Así, por ejemplo, si la primera coordenada de \( \nabla F(P) \times \nabla G(P) \) no es cero, entonces podemos usar \( x \) como parámetro y despejar \( y,z \) en función de \( x \) cerca de \( P \), en el sentido de que existen un intervalo \( I \subset \R \) centrado en el punto \( x_0 \) y dos únicas funciones escalares \( y(x) \) y \( z(x) \) de clase \( C^n(I) \) tales que \( y(x_0)=y_0 \), \( z(x_0)=z_0 \) y \( \bigl(x,y=y(x),z=z(x)\bigr) \) es una solución del sistema de ecuaciones \( F(x,y,z)=0 \), \( G(x,y,z)=0 \) para cada \( x \in I \). Además, las derivadas \( y'(x) \) y \( z'(x) \) vienen dadas para cada \( x \in I \) por la solución única del sistema de ecuaciones lineales
\[ \begin{align} F_y\bigl(x, y(x), z(x) \bigr) y'(x) + F_z \bigl(x, y(x), z(x) \bigr)z'(x) &=- F_x \bigl(x, y(x), z(x) \bigr) \notag \\ G_y\bigl(x, y(x), z(x) \bigr) y'(x) + G_z\bigl(x, y(x), z(x) \bigr) z'(x) &=-G_x\bigl(x, y(x), z(x) \bigr) \notag \end{align} \]
Se dice, en este caso, que las ecuaciones \( F(x,y,z)=0 \) y \( G(x,y,z)=0 \) definen implícitamente las variables \( y, z \) como funciones \( y(x), z(x) \) de la variable \( x \) cerca del punto \( P \).
En estas condiciones, el trozo de curva \( C \) cerca de \( P\) podemos parametrizarlo, usando \( x \) como parámetro, mediante \( {\vecs r}: x \in I \to {\vecs r}(x)=\bigl(x,y(x),z(x)\bigr) \). Entonces, un vector tangente a la curva en un punto \( \bigl( x,y=y(x),z=z(x) \bigr) \) es \({\vecs r}\,{}'(x)= \bigl( 1,y'(x),z'(x) \bigr) \) que, como se deduce del sistema de ecuaciones anterior, es ortogonal tanto a \( \nabla F \) como a \( \nabla G \) y, por tanto, paralelo al producto vectorial \( \nabla F \times \nabla G \), como habíamos adelantado.
Como en los casos de curvas en el plano y de superficies en el espacio, el papel de las variables es intercambiable, de manera que si la segunda coordenada de \( \nabla F(P)\times \nabla G(P) \) no es cero, entonces podemos usar \( y \) como parámetro y despejar \( x,z \) en función de \( y \) cerca de \( P \), mientras que si la tercera coordenada de \( \nabla F(P)\times \nabla G(P) \) no es cero, entonces podemos usar \( z \) como parámetro y despejar \( x,y \) en función de \( z \) cerca de \( P \).
Procedimiento de derivación implícita
Volviendo al caso en que las ecuaciones \( F(x,y,z)=0 \) y \( G(x,y,z)=0 \) definen implícitamente las variables \( y, z \) como funciones de la variable \( x \) cerca del punto \( P \), el procedimiento de derivación implícita para ir calculando las sucesivas derivadas de \( y(x) \) y \( z(x) \) consiste en derivar simultáneamente las dos igualdades \( F\bigl(x, y(x), z(x) \bigr)=0 \), \( G\bigl(x, y(x), z(x) \bigr)=0 \) para \( x \in I \), sustituir los valores previamente obtenidos y resolver el sistema corrrespondiente. Veamos un ejemplo.
Ejemplo. Consideremos la intersección de la superficie dada por \(x^2+y^2+z^3=2\) con el plano \( x+y+z=2\). El punto \(P=(0,1,1)\) está en dicha intersección. Los campos \( F(x,y,z)=x^2+y^2+z^3-2\) y \( G(x,y,z)=x+y+z-2\) son de clase \( C^\infty(\R^3) \). Además, \(\nabla F(x,y,z)=(2x, 2y, 3z^2) \) y \( \nabla G(x,y,z)=(1,1,1) \) cumplen que \( \nabla F(P)=(0,2,3) \) y \( \nabla G(x,y,z)=(1,1,1) \) son linealmente independientes y la primera componente de \( \nabla F(P) \times \nabla G(P) = (-1,3,-2) \) no es cero, así que el teorema de la función implícita nos dice que las ecuaciones \(x^2+y^2+z^3=2\) y \( x+y+z=2 \) definen implícitamente, cerca del punto \( P =(0,1,1) \), una curva \( C \) en la que las variables \( y, z \) son funciones \( y(x), z(x) \) de la variable \( x \) que se mueve en un intervalo \( I \) centrado en \( x_0=0 \) y cumplen \( y(0)=1, z(0)=1 \). Sería muy complicado calcular las expresiones explícitas de estas funciones \( y(x), z(x) \), pero podemos calcular sus derivadas en \( x_0=1\) y, por tanto, sus polinomios de Maclaurin.
Derivamos con respecto a \( x \) en las igualdades \(x^2+y^2+z^3=2\) y \( x+y+z=2 \), usando ya que \( y, z \) son funciones de \( x \in I \) (pero suprimiendo el argumento \( (x) \) de las funciones \( y(x), z(x), y'(x), z'(x), \ldots \) por claridad). Entonces nos queda \( 2x+2yy'+3z^2z'=0 \) y \(1+y'+z'=0 \) para \( x \in I \). Tomando \( x=0 \) y usando que \( y(0)=1, z(0)=1 \), obtenemos \( 2y'(0)+3z'(0)=0 \) e \( y'(0)+z'(0)=-1 \). Resolviendo este sistema obtenemos \(y'(0)=-3\) y \(z'(0)=2\).
Ahora, derivando con respecto a \( x \) las igualdades \( 2x+2yy'+3z^2z'=0 \) y \(1+y'+z'=0 \) para \( x \in I \), obtenemos \( 2+2(y')^2+2yy''+6z(z')^2+3z^2z'' =0 \) e \(y''+z''=0 \) para \( x \in I \). Poniendo \( x=0 \) y usando que \( y(0)=1, z(0)=1, y'(0)=-3, z'(0)=2 \), nos queda \(2y'(0)+3z'(0)=-44 \) e \( y''(0)+z''(0)=0\), con lo que \( y''(0)=44 \) y \(z''(0)=-44\).
Volviendo a derivar obtenemos \(6y'y''+2yy'''+6(z')^3+18zz'z''+3z^2z'''=0\) e \(y'''+z'''=0\) para \( x \in I \). Tomando \( x=0 \) y los valores anteriormente obtenidos queda \( 2y'''(0)+3z'''(0)=2328 \) e \( y'''(0)+z'''(0)=0 \). Resolviendo este sistema nos queda \(y'''(0)=-2328\) y \(z'''(0)=2328\). Entonces, los polinomios de Maclaurin de grado \( 3 \) de \( y(x) \) y \(z(x) \) son, respectivamente,
\[ y(x)\approx p_3(x)=1-3x+22x^2-388x^3, \qquad z(x)\approx q_3(x)=1+2x-22x^2+388x^3. \notag\]
En la figura vemos la superficie \(x^2+y^2+z^3=2\) (los tonos verdosos y violeta al fondo), el plano \( x+y+z=2 \) (en amarillo oscuro), el punto \(P=(0,1,1)\) (en negro) y la aproximación de la curva \( C \) (en rojo) dada por la parametrización \(x, y(x)\approx p_3(x), z(x)\approx q_3(x) \) con \( -0.05 < x < 0.05\).
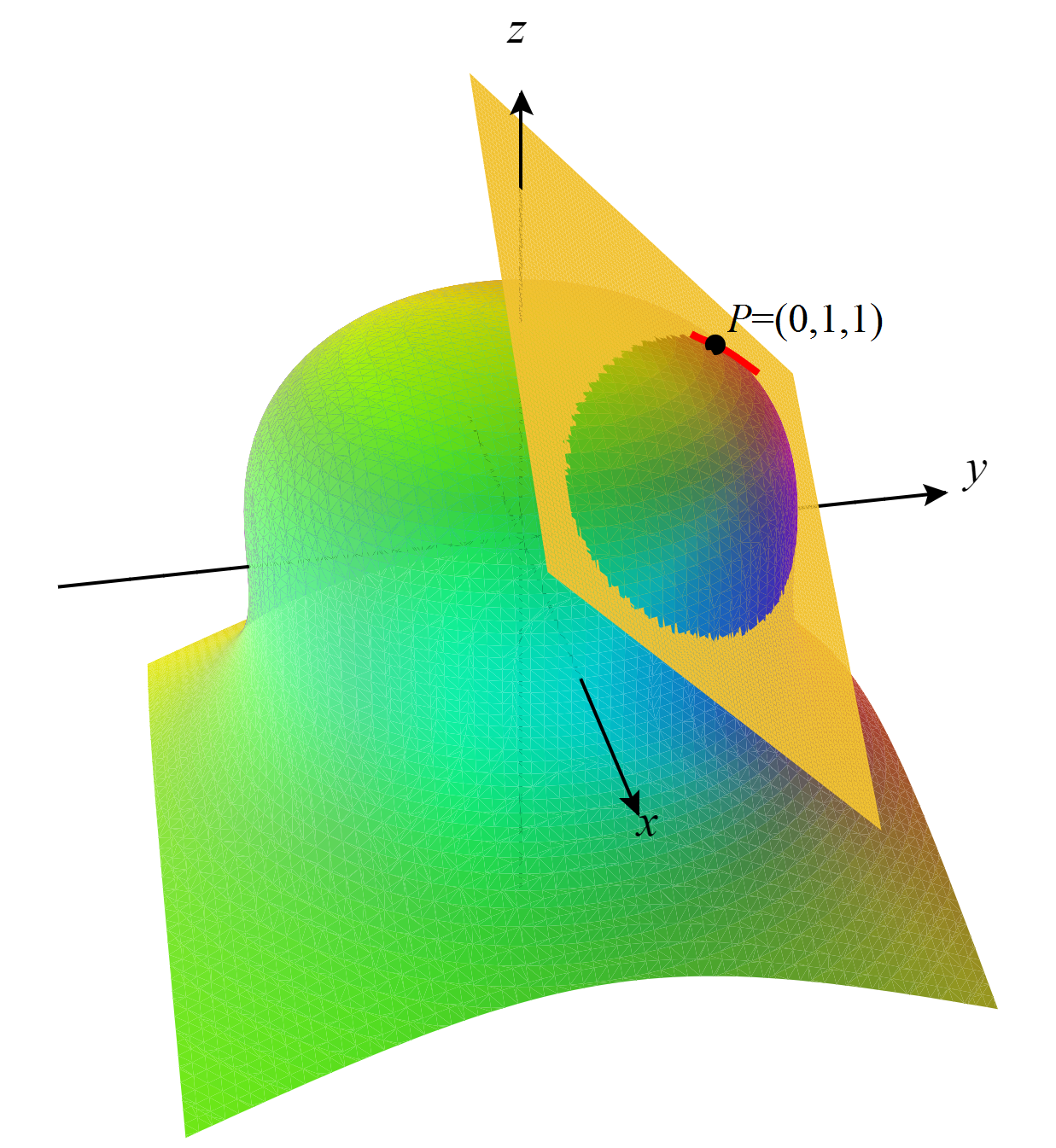
Corte de la superficie \(x^2+y^2+z^3=2\) con el plano \( x+y+z=2 \).
Ejercicios
Utiliza la aplicación CalcPlot3D para dibujar las gráficas de las superficies que aparecen en los ejercicios.
Ejercicio 1. Calcula la recta tangente en \( P=(0,0,2) \) a la curva \( C \) obtenida al cortar la esfera \(x^2 + y^2 + z^2 = 4 \) con el paraboloide \( x^2 + z^2 = y + 4\).
Ejercicio 2. Sea \( C \) la curva dada por la intersección del paraboloide \( z=2-(x^2+y^2)\) con el cilindro \( x^2+z^2=2x \). Calcula las ecuaciones continuas de la recta tangente a \( C \) en el punto \( P=(1,0,1) \).
Ejercicio 3. Sea \( C \) la elipse obtenida al cortar el elipsoide \( x^2 + 4y^2 + 3z^2 = 16 \) con el plano \( x+y+2z = 5 \). Prueba que cerca del punto \( P=(0,1,2)\) se pueden despejar las variables \( y \) y \( z \) de dicha elipse en función de la variable \(x \) y calcula los correspondientes polinomios de Maclaurin de grado \( 3\).
Ejercicio 4. Prueba que el sistema de ecuaciones \( x^2+zy^2+z^3=1 \), \( x+y+z=1 \) define implícitamente las variables \( y,z \) como funciones \( y(x),z(x) \) cerca de \( P=(0,0,1) \) y calcula los correspondientes polinomios de Maclaurin de grado \( 2 \) de dichas funciones \( y(x), z(x) \).
Ejercicio 5. Sea \( C \) la curva dada por la intersección de la esfera \( x^2+y^2+z^2=3\) con el cilindro \( x^2+y^2=2x \). Prueba que cerca de \(P=(1,1,1) \) se pueden despejar las variables \( x \) e \( y \) de la curva como funciones de \(z \) y calcula los polinomios de Taylor de orden 3 de las correspondientes funciones alrededor del punto \( z_0=1 \).
Ejercicio 6. Sea \( C \) la curva dada por las ecuaciones implícitas \(x+y+z^2=0 \) y \( x^3+y^3+z^3=3xyz \). Prueba que cerca del punto \(P=(1,-1,0) \) se pueden despejar las variables \( y,z \) de la curva como funciones de \( x \) y calcula los polinomios de Taylor de orden \( 3 \) de las correspondientes funciones alrededor del punto \( x_0=1 \).
Ejercicio 7. Sea \( S \) la superficie de ecuación implícita \( F(x,y,z)=x^{2}+y^{2}+z^{2}+4xy+z=1 \).
- Prueba que dicha ecuación implícita permite definir \( z \) como una función de \( x \) e \( y \), que denotaremos por \( z=f(x,y) \),cerca de \( P=(0,-1,0) \).
- Determina la dirección según la cual la derivada direccional de \( f \) en el punto \( (0,-1) \) es máxima y calcula el valor de dicha derivada direccional.
- Determina la ecuación del plano tangente a \( S \) en \( P \).
- Al cortar la superficie \( S \) con el cilindro de ecuación \( x^{2}+y^{2}=1 \) se obtiene una curva \( C \) que pasa por \( P \). Halla la recta tangente a la curva \( C \) en el punto \( P \) y su curvatura en dicho punto \( P \).
Ejercicio 8. Sea \( C \) la curva dada por las ecuaciones \( y^2+z^2-x^2+2=0 \) e \( yz+xz-xy-1=0 \).
- Prueba que es posible parametrizar un tramo de \( C \) cerca del punto \( P=(2,1,1) \) tomando la variable \( x \) como parámetro.
- Halla el vector \( \vecs{u} \) que es tangente a la curva \( C \) en el punto \( P \), es unitario y apunta en el sentido de subida de \( C \) en dicho punto.
- Dado el campo escalar \( f(x,y,z)=-xy-y^2+xyz+z^2+2y-2 \), halla la derivada direccional de \( f \) en \( P \) en la dirección de \( \vecs{u} \).

