6.1 Integrales de Línea
- Page ID
- 2923
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vector}[1]{\vec{\mathbf{#1}}}\)
\( \newcommand{\Disco}{\Bbb D}\)
\( \newcommand{\C}{\Bbb C}\)
\( \newcommand{\Q}{\Bbb Q}\)
\( \newcommand{\R}{\Bbb R}\)
\( \newcommand{\K}{\Bbb K}\)
\( \newcommand{\N}{\Bbb N}\)
\( \newcommand{\Z}{\Bbb Z}\)
\( \newcommand{\bo}{\textbf O}\)
\( \newcommand{\eps}{\varepsilon}\)
\( \newcommand{\la}{\lambda}\)
\( \newcommand{\om}{\omega}\)
\( \newcommand{\bmatriz}{\bmatrix \format \r&&\quad\r\\}\)
\( \newcommand{\bmatrize}{\bmatrix \format \c&&\quad\c\\}\)
\( \newcommand{\sep}{\, \equiv \,}\)
\( \newcommand{\xsep}{\quad \equiv \quad}\)
\( \newcommand{\xlsep}{\qquad \equiv \qquad}\)
\( \newcommand{\matriz}{\bmatrix\format\r&&\quad\r\\}\)
\( \newcommand{\endmatriz}{\endbmatrix}\)
\( \newcommand{\conj}[1]{\overline{}[1]}}\)
\( \newcommand{\vector}[1]{\vec{\textbf {}[1]}}}\)
\( \newcommand{\abs}[1]{\left\vert {#1} \right\vert}}\)
\( \newcommand{\norm}[1]{\left\Vert {#1}\right\Vert}\)
\( \newcommand{\bil}[2]{\left\langle {#1},{#2} \right\rangle}\)
\( \newcommand{\absbil}[2]{\abs{ \bil{#1}{#2} }}\)
\( \newcommand{\vectori}{\vector{\mathbf{\i}}}\)
\( \newcommand{\vectorj}{\vector{\mathbf{\j}}}\)
\( \newcommand{\vectork}{\vector{\mathbf{k}})\)
\( \newcommand{\vectorr}{\vector r}\)
\( \newcommand{\vectorrp}{\vector r}\,{}'}\)
\( \newcommand{\vectorrs}{\vector r}\,{}''}\)
\( \newcommand{\parteim}{\mathop{\text{Im}}\nolimits}\)
\( \newcommand{\partere}{\mathop{\text{Re}}\nolimits}\)
\( \newcommand{\sen}{\mathop{\text{sen}}\nolimits}\)
\( \newcommand{\sinc}{\mathop{\text{sinc}}\nolimits}\)
\( \newcommand{\sa}{\mathop{\text{sa}}\nolimits}\)
\( \newcommand{\senh}{\mathop{\text{senh}}\nolimits}\)
\( \newcommand{\arsenh}{\mathop{\text{arsenh}}\nolimits}\)
\( \newcommand{\arcosh}{\mathop{\text{arcosh}}\nolimits}\)
\( \newcommand{\Log}{\mathop{\text{Log}}\nolimits}\)
\( \newcommand{\Ln}{\mathop{\text{Ln}}\nolimits}\)
\( \newcommand{\Arg}{\mathop{\text{Arg}}\nolimits}\)
\( \newcommand{\arcsen}{\mathop{\text{arcsen}}\nolimits}\)
\( \newcommand{\arcos}{\mathop{\text{arccos}}\nolimits}\)
\( \newcommand{\arctg}{\mathop{\text{arctg}}\nolimits}\)
\( \newcommand{\ran}{\mathop{\text{ran}}\nolimits}\)
\( \newcommand{\maxe}{\mathop{\text{máx}}}\)
\( \newcommand{\mine}{\mathop{\text{mín}}}\)
\( \newcommand{\lime}{\mathop{\text{lím}}}\)
\( \newcommand{\lin}{\mathop{\text{lin}}\nolimits}\)
\( \newcommand{\inte}{\mathop{\text{int}}\nolimits}\)
\( \newcommand{\grad}{\mathop{\text{grad}}\nolimits}\)
\( \newcommand{\signo}{\mathop{\text{sig}}\nolimits}\)
\( \newcommand{\fl}{\mathop{\text{flot}}\nolimits}\)
\( \newcommand{\essup}{\mathop{\text{ess}\,\text{sup}}\nolimits}\)
\( \newcommand{\card}{\mathop{\text{card}}\nolimits}\)
\( \newcommand{\rot}{\mathop{\text{rot}}\nolimits}\)
\( \newcommand{\diver}{\mathop{\text{div}}\nolimits}\)
\( \newcommand{\volum}{\mathop{\text{vol}}\nolimits}\)
\( \newcommand{\Res}{\mathop{\text{Res}}\nolimits}\)
\( \newcommand{\grado}{\mathop{\text{gr}}\nolimits}\)
\( \newcommand{\dpar}[2]{\dfrac{\partial{#1}}{\partial{#2}}}\)
\( \newcommand{\dparx}[1]{\dfrac{\partial {#1}}{\partial x}}}\)
\( \newcommand{\dpary}[1]{\dfrac{\partial {#1}}{\partial y}}}\)
\( \newcommand{\dparz}[1]{\dfrac{\partial {#1}}{\partial z}}}\)
\( \newcommand{\dparr}[1]{\dfrac{\partial {#1}}{\partial r}}}\)
\( \newcommand{\dparth}[1]{\dfrac{\partial {#1}}{\partial \theta}}}\)
\( \newcommand{\dparxx}[1]{\dfrac{\partial^2 {#1}}{\partial x^2}}}\)
\( \newcommand{\dparyy}[1]{\dfrac{\partial^2 {#1}}{\partial y^2}}}\)
\( \newcommand{\dparxy}[1]{\dfrac{\partial^2 {#1}}{\partial x \partial y}}}\)
\( \newcommand{\dparzz}[1]{\dfrac{\partial^2 {#1}}{\partial z^2}}}\)
\( \newcommand{\dparxz}[1]{\dfrac{\partial^2 {#1}}{\partial x \partial z}}}\)
\( \newcommand{\dparyz}[1]{\dfrac{\partial^2 {#1}}{\partial y \partial z}}}\)
\( \newcommand{\dpardos}[2]{\dfrac{\partial^2 {#1}}{\partial {#2}^2}}}\)
\( \newcommand{\dparcruz}[3]{\dfrac{\partial^2 {#1}}{\partial {#2} \partial {#3}}}\)
\( \newcommand{\dtan}[1]{ \dfrac{\partial {#1}}{\partial {\vector t}} }}\)
\( \newcommand{\dnormal}[1]{ \dfrac{\partial {#1}}{\partial {\vector n}} }}\)
Muchos conceptos físicos, como el de trabajo desarrollado por una fuerza, se expresan en términos del comportamiento de un campo vectorial a lo largo de una curva, para lo que es necesario extender el concepto de integral. En los cursos de cálculo con una variable has estudiado la integral de una función continua en un intervalo. En esta lección estudiamos las integrales de línea, sustituyendo el intervalo por una curva en \(\R^3\) (para trabajar en \(\R^2\) basta con suprimir la tercera coordenada) y la función por un campo escalar o vectorial continuo sobre esa curva. En la mayoría de las aplicaciones de los conceptos y teoremas que veremos en esta lección las variables \(x\), \(y\) y \(z\) representan coordenadas espaciales, por eso trabajaremos con gradientes en vez de diferenciales.
Sea \(C\) una curva regular a trozos parametrizada por \(\vecs r(t)\), con \(t \in [a,b]\), y sea \(\vecs F:C\to \R^3\) un campo vectorial continuo. La integral de línea de \(\vecs F\) sobre \(C\) se define como
\[ \int_C \vecs F \cdot d\vecs r = \int_a^b \vecs F\big(\vecs r(t) \big) \cdot \vecs r'(t) \, dt. \]
Cuando la curva es cerrada, se usa una notación especial que destaca este hecho: \(\displaystyle \oint_C\vecs F\cdot d\vecs r\) en cuyo caso la integral también se denomina circulación de \(\vecs F\) a lo largo de \(C\).
Si la parametrización y el campo vectorial vienen dados por sus componentes, \(\vecs r(t)=\big(x(t),y(t),z(t)\big)\) y \(\vecs F(x,y,z)=\big(P(x,y,z), \, Q(x,y,z), \, R(x,y,z) \big)\), entonces la integral queda
\[ \int_C \vecs F\cdot d\vecs r= \int_a^b \big[ P\big(x(t),y(t), z(t)\big) x'(t) + Q\big(x(t),y(t), z(t)\big) y'(t) + R\big(x(t),y(t), z(t)\big) z'(t) \big] \,dt \]
por lo que otra notación muy habitual para estas integrales de línea es
\[ \int_C \vecs F\cdot d\vecs r=\int_C P\,dx \, + \, Q\,dy \, + \, R\,dz. \]
Para el caso bidimensional \( \vecs F(x,y)=\big(P(x,y),Q(x,y)\big) \) se escribe
\[ \int_C {\vecs F}\cdot d{\vecs r}=\int_C P\,dx \, + \, Q\,dy. \]
Propiedades de las integrales de línea de campos vectoriales. Sea \(C\) una curva regular a trozos parametrizada por \(\vecs r (t)\), con \(t\in [a,b]\), y sean \(\vecs F, \vecs G:C \to\R^3\) campos vectoriales continuos.
\(\rm{L\small{INEALIDAD}}\): si \(\lambda\) y \(\mu\) son números reales entonces \(\displaystyle \int_C \left( \lambda\vecs F+\mu\vecs G \right)\cdot d{\vecs r} = \lambda\int_C \vecs F\cdot d{\vecs r} +\mu\int_C \vecs G\cdot d{\vecs r}\)
\(\rm{A\small{DITIVIDAD}}\): si \(C\) puede descomponerse en dos curvas \(C_1\) y \(C_2\) que no se solapan, entonces
\[ \int_C \vecs F \cdot d\vecs r = \int_{C_1} \vecs F \cdot d\vecs r + \int_{C_2} \vecs F\cdot d\vecs r. \]
\(\rm{D\small{EPENDENCIA \,DE \,LA \,ORIENTACIÓN}}\): El valor absoluto de \(\int_C \vecs F\cdot d\vecs r\) no depende de la parametrización elegida, pero su signo sí. Si \(\vecs {r}_1\) es una parametrización de \(C\) con la misma orientación que \(\vecs r\) entonces \(\int_C \vecs F\cdot d\vecs r =\int_C \vecs F\cdot d{\vecs {r}_1}\), mientras que si \(\vecs {r}_2\) es una parametrización de \(C\) con orientación opuesta a \(\vecs r\), entonces \(\int_C \vecs F\cdot d\vecs r =- \int_C \vecs F\cdot d\vecs {r}_2\).
Observación. Sea \(\vecs r(t)\), con \(t \in [a,b]\), una parametrización regular de la curva \(C\). Entonces, usando que \(\|\vecs r'(t)\|\neq 0\), podemos escribir
\[ \int_C \vecs F\cdot d{\vecs r}= \int_a^b \vecs F\big( \vecs r(t) \big) \cdot \vecs r'(t)\,dt= \int_a^b \vecs F\big( \vecs r(t) \big) \cdot \dfrac{ \vecs r'(t)}{\|\vecs r'(t)\|} {\|\vecs r'(t)\|}\, dt. \]
El vector \(\vecs r'(t) \big / \|\vecs r'(t)\|\) que aparece en esta integral es el vector tangente unitario \(\vecs T\), de manera que \(\vecs F\cdot(\vecs r’ / \|\vecs r'\| ) = \vecs F \cdot \vecs T\) es la componente tangencial del campo \(\vecs F\) a lo largo de la curva y se tiene \(\displaystyle\int_C \vecs F\cdot d\vecs r= \int_a^b \vecs F\cdot \vecs T \,\|\vecs r'(t)\|\, dt.\) Por su analogía con la integral \(\displaystyle\int_a^b \|\vecs r'(t)\|\,dt\) que nos da la longitud de \(C\), la integral de línea también se suele escribir como \(\displaystyle \int_C \vecs F\cdot {\vecs T} \, ds\), o bien \(\displaystyle \int_C \vecs F\cdot {\vecs T} \, |d\vecs r|\), donde "ds" y "\(|d\vecs r|\)"se lee "diferencial de la longitud de arco".
Integrales de línea de campos escalares con respecto a la longitud de arco. Sea \(C\) una curva regular a trozos parametrizada por \(\vecs r(t)\) para \(t \in [a,b]\) y sea\( f \colon C\to\R\) un campo escalar continuo. La integral de línea con respecto a la longitud de arco de \(f\) sobre \(C\) se define como
\[ \int_C f \,ds = \int_a^b f\big( \vecs r(t) \big) \|\vecs r'(t)\| \, dt \] donde "ds" se lee "diferencial de arco". Otra notación habitual es \(\displaystyle \int_C f \, |d \vecs r|\). Además, cuando la curva es cerrada, se usa una notación especial que destaca este hecho: \(\displaystyle\oint_C f \, ds \).
En el caso de una curva plana y un campo escalar de dos variables, podemos interpretar geométricamente la integral de línea de un campo positivo \(f\) sobre \(C\) de la siguiente manera: Cortamos la superficie \(z=f(x,y)\) verticalmente a lo largo de la curva \(C\) ; es decir, sobre cada punto \((x,y)\) de la curva levantamos una línea vertical de altura \(z=f(x,y)\). El resultado es como una valla vertical cuya altura va cambiando. La integral de \(f\) sobre \(C\) es el área de dicha valla.
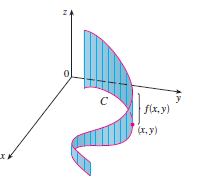
En particular, para el campo \(f=1\) la integral de línea nos proporciona la longitud de la curva
\[ \int_C 1 \,ds = \int_a^b \|\vecs r'(t)\| \, dt =\text{longitud de }C.\]
El teorema del cambio de variable para integrales nos permite probar que el valor de la integral no depende de la parametrización elegida (sea la curva recorrida en el mismo sentido o en sentido contrario). Si, en particular, \(C\) es una curva regular de longitud \(L\) y tomamos la parametrización natural \(\vecs r_{n}\colon [0,L] \to C\) donde \(s\) es el parámetro longitud de arco , entonces sabemos que \(\|\vecs r'_{n}(s)\|=1\), luego
\[ \int_C f \,ds=\int_0^L f\big( \vecs r_{\text{n}} (s) \big) \, ds \] que es de donde viene la notación.
Propiedades de las integrales de línea con respecto a la longitud de arco. Sea \(C\) una curva regular a trozos parametrizada por \({r} ^3\) y sean \(f\), \(g: C\) sendos campos escalares continuos en \(C\).
\(\mathbf{(1)}\) Linealidad: si \(\lambda\) y \(\mu\) son números reales, entonces \(\displaystyle\int_C (\lambda f +\mu g )\, ds = \lambda\int_C f \, ds +\mu\int_C g \,ds.\)
\(\mathbf{(2)}\) Monotonía: si \(f(x) \leq g(x)\) para todo \(x \in C\), entonces \(\displaystyle\int_C f \,ds \leq \int_C g \, ds.\)
\(\mathbf{(3)}\) Aditividad: si \(C\) puede escribirse como la unión de dos curvas \(C_1\) y \(C_2\), entonces \(\displaystyle\int_C f \,ds = \int_{C_1} f \, ds + \int_{C_2} f \, ds.\) Esta propiedad facilita los cálculos en el caso en que distintas porciones de la curva se parametrizan mediante fórmulas distintas; un polígono, por ejemplo.
EJERCICIOS DE LA SECCIÓN 1
Ejercicio 1. Sea \(C\) el arco de la curva de ecuación \(y=x^3\) recorrido desde el punto \((0,0)\) hasta el punto \((1,1)\). Calcula la integral de línea del campo vectorial \(\vecs F(x,y)=(y^3,x^3+3xy^2)\) sobre \(C\).
Ejercicio 2. Sea \(C\) el rectángulo de vértices \((0,0)\), \((1,0)\), \((1,2)\), \((0,2)\). Halla \(\displaystyle \oint_{C}(2xy-x^{2},x+y^{2})\cdot d\vecs r\).
Ejercicio 3. Sea \(C\) la curva cerrada formada por los arcos de las parábolas \(y=x^{2}\) e \(y^{2}=x\) recorrida en sentido positivo. Calcula \(\displaystyle \oint_{C}(xy,x+y)\cdot d\vecs r\).
Ejercicio 4. Calcula \(\displaystyle \oint_{C}(-y,x^{2}+2)\cdot d\vecs r\), donde \(C\) es la circunferencia de centro el origen y radio \(a\) orientada en sentido positivo.
Ejercicio 5. Calcula \(\displaystyle \oint_{C}\big(-y^{3}\,dx+x^{3}\,dy\big)\) sobre el triángulo \(C\) de vértices \((0,0)\), \((1,0)\) y \((0,2)\).
Ejercicio 6. Calcula \(\displaystyle \oint_{C}2xy\,dx+(y^{2}-x^{2})\,dy\), donde \(C\) es la cardioide de ecuación \(r=1+\cos(\theta)\) orientada en sentido antihorario.
Ejercicio 7. Calcula \(\displaystyle \int_{C}(x^{2}-2xy,y^{2}-2xy)\cdot d\vecs r\), donde \(C\) es el arco de la parábola \(y=x^{2}\) comprendido entre \((-1,1)\) y \((1,1)\).
Ejercicio 8. Dados los puntos \(O=(0,0,0)\), \(A=(1,0,0)\), \(B=(1,1,0)\) y \(P=(1,1,1)\), calcula la integral de línea \(\displaystyle\int_{C} y\,dx-(x-y)\,dy+x\,dz\) a lo largo de cada una de las tres curvas que tienen \(O\) como punto inicial y \(P\) como punto final dadas a con-ti-nua-ción: (1) La diagonal \(OP\), (2) las aristas del cubo \(OABP\) y (3) la quebrada \(OBP\).
Ejercicio 9. Calcula la integral de línea del campo \(\vecs F(x,y,z)=(yz,xz,xy)\) sobre el segmento parametrizado por \(\vecs r(t)=(1+t,-1+t,1+2t)\) para \(t\in [0,1]\).
Ejercicio 10. Sea \(C\) la hélice \(\vecs r(t)=(2\cos (t),2\,\text{sen}(t),t/3)\), con \(t\in [0,4\pi ]\). Halla \(\displaystyle \int_{C}(x,zy,y)\cdot d\vecs r\).
Ejercicio 11. Calcula \(\displaystyle\int_{C}z\,dz\), siendo \(C\) la hélice cónica \(\vecs r(t)=(t\cos (t),t\,\text{sen}(t),t)\), para \(t\in [0,6\pi ]\).
Ejercicio 12. Calcula \(\displaystyle \oint_{C}y\,dx+z\,dy+x\,dz\), donde \(C\) es la curva intersección de las superficies \(z=xy\) y \(x^{2}+y^{2}=1\) con orientación positiva si se mira la curva desde arriba.
Ejercicio 13. Calcula \(\displaystyle \oint_{C}(y-z)\,dx+(z-x)\,dy+(x-y)\,dz\), siendo \(C\) el triángulo de vértices \((a,0,0)\), \((0,b,0)\) y \((0,0,c)\) recorrido en este sentido.
Ejercicio 14. Calcula la integral \(\displaystyle \int_C x^2 y \,ds\) sobre las siguientes curvas.
(2) La semicircunferencia \(x^2 + y^2 = 1\), con \(x ⩽ 0.\)
(3) La quebrada que une consecutivamente los puntos \((1, 1), \,(1, 0)\) y \((0, 1).\)
(4) El segmento que une los puntos \((1, 2)\) y \((3, −1).\)
Ejercicio 15. Prueba la siguiente propiedad de la cicloide: Si un punto se desliza por la cicloide (invertida), sin velocidad inicial, desde un punto \(A\) hasta el punto más bajo \(B\) sujeto únicamente a la acción de la gravedad, entonces el tiempo que tarda en llegar hasta \(B\) es el mismo sea cual sea el punto \(A\) de partida (esta propiedad se conoce como tautocronía). Para ello, utiliza que la velocidad es \(ds/dt = \sqrt{2gy}\), siendo \(y\) la distancia bajada medida en vertical, de manera que el tiempo que se tarda en recorrer un arco \(C\) de cicloide es \(\displaystyle t = \int_C \frac{ds}{\sqrt{2gy}}.\)
Ejercicio 16. Calcula las siguientes integrales con respecto a la longitud de arco.
(2) \(\displaystyle\int_C y^2 \,ds\), siendo \(C\) la cicloide generada por una circunferencia de radio unidad.
(3) \(\displaystyle\int_C x^2 y^2 \,ds\), siendo \(C\) la circunferencia unidad.
(4) \(\displaystyle\int_C (x + y) \,ds\), donde \(C\) es el triángulo de vértices \((0, 0), \,(1, 0)\) y \((0, 1).\)
(5) \(\displaystyle\int_C 2xy \,ds\), siendo \(C\) la curva cerrada formada por los arcos de las parábolas \(y = x^2\) e \(y^2 = x\) con \(0 ≤ x ≤ 1\) y \(0 ≤ y ≤ 1.\)
Ejercicio 17. Dada la función \(f(x, y) = x^2 y^2\), calcula las integrales de \(f\) con respecto a la longitud de arco sobre las curvas dadas por las siguientes parametrizaciones.
(2) \(\vecs r_2(t) = (\cos(2t), \text{sen}(2t))\), con \(t ∈ [0, 2π].\)
(3) \(\vecs r_3(t) = (\cos(t), − \text{sen}(t))\), con \(t ∈ [0, 2π].\)
Observa que las tres son parametrizaciones distintas de la circunferencia unidad. ¿Cómo se recorre la circunferencia en cada caso?, ¿cómo influyen los diferentes recorridos en el valor de la integral?

