10: El Péndulo Simple

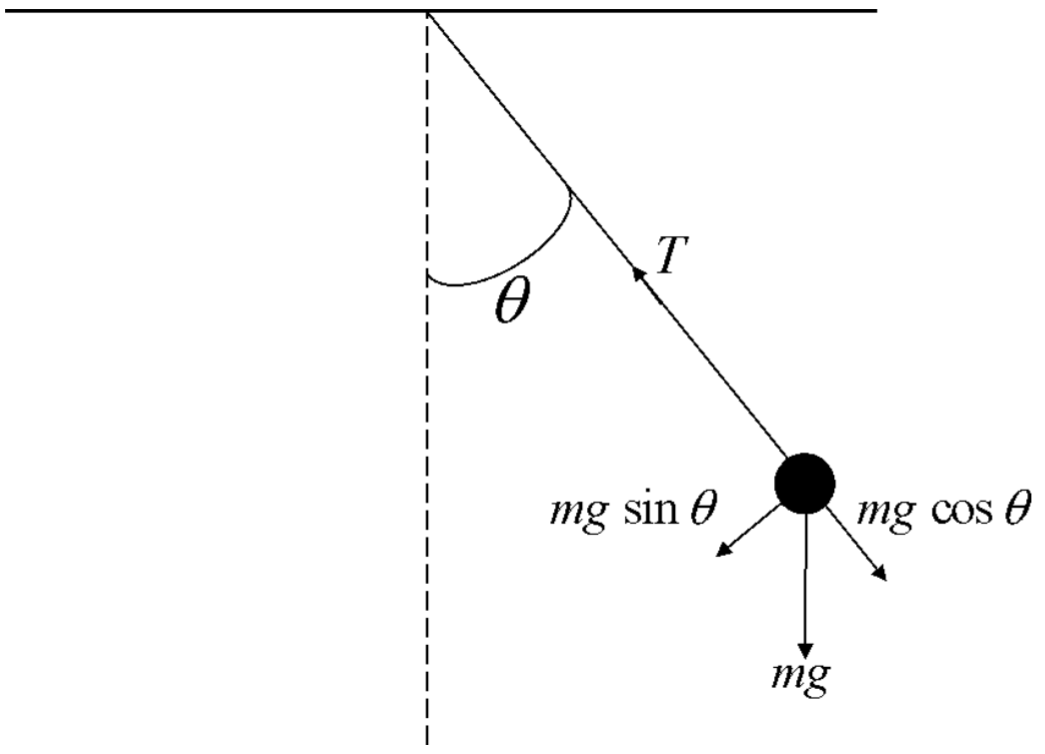
Primero consideramos el péndulo simple que se muestra en la Fig. 10.1. Una masa se une a una varilla rígida sin masa, y se limita a moverse a lo largo de un arco de un círculo centrado en el punto de pivote. Supongamos que\(l\) es la longitud fija de la biela, y\(\theta\) es el ángulo que hace con el eje vertical. Derivaremos las ecuaciones gobernantes para el movimiento de la masa, y una ecuación que puede resolverse para determinar el período de oscilación.

Ecuaciones de gobierno

Las ecuaciones gobernantes para el péndulo se derivan de la ecuación de Newton,\(F=m a .\) Debido a que el péndulo está constantado para moverse a lo largo de un arco, podemos escribir la ecuación de Newton directamente para el desplazamiento\(s\) del péndulo a lo largo del arco con origen en la parte inferior y positivo dirección a la derecha.

La fuerza relevante sobre el péndulo es la componente de la fuerza gravitacional a lo largo del arco, y de la Fig. \(10.1\)se ve que es

\[F_{g}=-m g \sin \theta, \nonumber \]

donde el signo negativo significa una fuerza que actúa a lo largo de la\(s\) dirección negativa cuando\(0<\theta<\pi\), y la\(s\) dirección positiva cuando\(-\pi<\theta<0\).

La ecuación de Newton para el péndulo simple que se mueve a lo largo del arco es por lo tanto

\[m \ddot{s}=-m g \sin \theta . \nonumber \]

Ahora, la relación entre la longitud del arco\(s\) y el ángulo\(\theta\) viene dada por\(s=l \theta\), y por lo tanto\(\ddot{s}=l \ddot{\theta} .\) La ecuación simple del péndulo se puede escribir entonces en términos del ángulo\(\theta\) como

\[\ddot{\theta}+\omega^{2} \sin \theta=0, \nonumber \]

con

\[\omega=\sqrt{g / l} \nonumber \]

La aproximación estándar de ángulo pequeño\(\sin \theta \approx \theta\) da como resultado la conocida ecuación para el oscilador armónico simple,

\[\ddot{\theta}+\omega^{2} \theta=0 . \nonumber \]

Hemos derivado las ecuaciones de movimiento suponiendo que el péndulo está limitado a moverse a lo largo del arco de un círculo. Tal restricción es válida siempre que la masa del péndulo esté conectada a una varilla rígida sin masa. Si la varilla es reemplazada por un resorte sin masa, digamos, entonces pueden ocurrir oscilaciones en la longitud del resorte. Derivar las ecuaciones para esta situación física más general requiere considerar la forma vectorial de la ecuación de Newton.

Figura 10.1: Fuerzas que actúan sobre el péndulo.

Es informativo construir las ecuaciones gobernantes equivalentes en coordenadas polares. Para ello, formamos la coordenada compleja\(z=x+i y\), y hacemos uso de la forma polar para\(z\), dada por

\[z=r e^{i \theta} . \nonumber \]

Las ecuaciones gobernantes se convierten entonces

\[\frac{d^{2}}{d t^{2}}\left(r e^{i \theta}\right)=g-\frac{T}{m} e^{i \theta} \nonumber \]

La segunda derivada se puede calcular usando las reglas de producto y cadena, y uno encuentra

\[\frac{d^{2}}{d t^{2}}\left(r e^{i \theta}\right)=\left(\left(\ddot{r}-r \dot{\theta}^{2}\right)+i(r \ddot{\theta}+2 \dot{r} \dot{\theta})\right) e^{i \theta} . \nonumber \]

Dividiendo ambos lados de\((10.7)\) por\(e^{i \theta}\), obtenemos

\[\left(\ddot{r}-r \dot{\theta}^{2}\right)+i(r \ddot{\theta}+2 \dot{r} \dot{\theta})=g e^{-i \theta}-\frac{T}{m} . \nonumber \]

Las dos ecuaciones gobernantes en coordenadas polares, entonces, se determinan equiparando las partes reales y las partes imaginarias de\((10.9)\), y encontramos

\[\begin{align} &\ddot{r}-r \dot{\theta}^{2}=g \cos \theta-\frac{T}{m} \\ &r \ddot{\theta}+2 \dot{r} \dot{\theta}=-g \sin \theta \end{align} \nonumber \]

Si el conector es una varilla rígida, como asumimos inicialmente, entonces\(r=l, \dot{r}=0\), y\(\ddot{r}=0 .\) La primera ecuación\((10.10)\) es entonces una ecuación para la tensión\(T\) en la varilla, y la segunda ecuación (10.11) reduce a nuestra derivada previamente (10.3). Si el conector es un resorte, entonces se puede aplicar la ley de Hooke. Supongamos que la constante de resorte es\(k\) y el resorte no estirado tiene longitud\(l\). Entonces

\[T=k(r-l) \nonumber \]

en\((10.10)\), y un par de ecuaciones simultáneas de segundo orden gobiernan el movimiento. El equilibrio estable con la masa en reposo en el fondo satisface\(\theta=0\) y\(r=l+m g / k ;\) es decir, el resorte se estira para contrarrestar la masa colgante.

Periodo de movimiento

En general, el periodo del péndulo simple depende de la amplitud de su movimiento. Para pequeñas oscilaciones de amplitud, la ecuación de péndulo simple se\((10.3)\) reduce a la ecuación de oscilador armónico simple (10.5), y el período se vuelve independiente de la amplitud. La solución general de la ecuación simple del oscilador armónico se puede escribir como

\[\theta(t)=A \cos (\omega t+\varphi) \nonumber \]

Condiciones iniciales sobre\(\theta\) y\(\dot{\theta}\) determinar\(A\) y\(\varphi\), y redefiniendo el origen del tiempo, siempre se puede elegir\(\varphi=0\) y\(A>0\). Con esta elección,\(A=\theta_{m}\), la amplitud máxima del péndulo, y la solución analítica de\((10.5)\) es

\[\theta(t)=\theta_{m} \cos \omega t \nonumber \]

donde\(\omega\) se llama la frecuencia angular de oscilación. El período de movimiento está relacionado con la frecuencia angular por

\[T=2 \pi / \omega, \nonumber \]

y es independiente de la amplitud\(\theta_{m}\).

Si ya no\(\sin \theta \approx \theta\) es una aproximación válida, entonces necesitamos resolver la ecuación de péndulo simple (10.3). Primero derivamos una expresión analítica de forma cerrada, y luego explicamos cómo calcular una solución numérica.

Solución analítica

Un procedimiento estándar para resolver ecuaciones diferenciales desconocidas es tratar de determinar alguna combinación de variables que sea independiente del tiempo. Aquí, podemos multiplicar\((10.3)\) por\(\dot{\theta}\) para obtener

\[\dot{\theta} \ddot{\theta}+\omega^{2} \dot{\theta} \sin \theta=0 . \nonumber \]

Ahora,

\[\dot{\theta} \ddot{\theta}=\frac{d}{d t}\left(\frac{1}{2} \dot{\theta}^{2}\right), \quad \dot{\theta} \sin \theta=\frac{d}{d t}(-\cos \theta), \nonumber \]

para que\((10.16)\) pueda escribirse como

\[\frac{d}{d t}\left(\frac{1}{2} \dot{\theta}^{2}-\omega^{2} \cos \theta\right)=0 \nonumber \]

La combinación de variables entre paréntesis es, por lo tanto, independiente del tiempo y se denomina integral de movimiento. También se dice que se conserva, y\((10.18)\) se le llama ley de conservación. En física, esta integral del movimiento (multiplicada por\(m l^{2}\)) se identifica con la energía del oscilador.

El valor de esta integral de movimiento\(t=0\) es dado por\(-\omega^{2} \cos \theta_{m}\), por lo que la ley de conservación derivada toma la forma

\[\frac{1}{2} \dot{\theta}^{2}-\omega^{2} \cos \theta=-\omega^{2} \cos \theta_{m}, \nonumber \]

que es una ecuación diferencial de primer orden separable.

Podemos calcular el periodo de oscilación\(T\) como cuatro veces el tiempo que tarda el péndulo en pasar de su altura inicial al fondo. Durante este trimestre de ciclo de oscilación, de\(d \theta / d t<0\) manera que a partir de (10.19),

\[\frac{d \theta}{d t}=-\sqrt{2} \omega \sqrt{\cos \theta-\cos \theta_{m}} . \nonumber \]

Después de separarnos e integrarnos durante un trimestre, tenemos

\[\int_{0}^{T / 4} d t=-\frac{\sqrt{2}}{2 \omega} \int_{\theta_{m}}^{0} \frac{d \theta}{\sqrt{\cos \theta-\cos \theta_{m}}} \nonumber \]

o

\[T=\frac{2 \sqrt{2}}{\omega} \int_{0}^{\theta_{m}} \frac{d \theta}{\sqrt{\cos \theta-\cos \theta_{m}}} \nonumber \]

Podemos transformar esta ecuación para el periodo en una forma más estándar usando una identidad trigonométrica y una sustitución. La identidad de trazo es la conocida fórmula de medio ángulo para el pecado, dada por

\[\sin ^{2}(\theta / 2)=\frac{1}{2}(1-\cos \theta) \nonumber \]

Usando esta identidad, escribimos

\[\cos \theta=1-2 \sin ^{2}(\theta / 2), \quad \cos \theta_{m}=1-2 \sin ^{2}\left(\theta_{m} / 2\right) \nonumber \]

y sustituir (10.24) en (10.19) resulta en

\[T=\frac{2}{\omega} \int_{0}^{\theta_{m}} \frac{d \theta}{\sqrt{\sin ^{2}\left(\theta_{m} / 2\right)-\sin ^{2}(\theta / 2)}} . \nonumber \]

Ahora definimos la constante

\[a=\sin \left(\theta_{m} / 2\right) \nonumber \]

y realizar la sustitución

\[\sin \phi=\frac{1}{a} \sin (\theta / 2) \nonumber \]

Desarrollando esta sustitución, tenemos

\[\cos \phi d \phi=\frac{1}{2 a} \cos (\theta / 2) d \theta . \nonumber \]

Ahora,

\[\begin{aligned} \cos (\theta / 2) &=\sqrt{1-\sin ^{2}(\theta / 2)} \\ &=\sqrt{1-a^{2} \sin ^{2} \phi} \end{aligned} \nonumber \]

para que\((10.28)\) pueda resolverse para\(d \theta\):

\[d \theta=\frac{2 a \cos \phi}{\sqrt{1-a^{2} \sin ^{2} \phi}} d \phi . \nonumber \]

Utilizando\((10.27)\), el dominio de integración\(\theta \in\left[0, \theta_{m}\right]\) se transforma en\(\phi \in[0, \pi / 2] .\) Por lo tanto, sustituyendo (10.27) y (10.29) en (10.25) da como resultado la ecuación estándar para el periodo dado por

\[T=\frac{4}{\omega} \int_{0}^{\pi / 2} \frac{d \phi}{\sqrt{1-a^{2} \sin ^{2} \phi}} \nonumber \]

con\(a\) dado por (10.26). La integral\(T=T(a)\) se llama la integral elíptica completa del primer tipo.

Para pequeñas amplitudes de oscilación, es posible determinar la dependencia del orden de avance del período sobre\(\theta_{m}\). Ahora\(a\) se da por\((10.26)\), para que una serie de Taylor a los rendimientos de orden principal

\[a^{2}=\frac{1}{4} \theta_{m}^{2}+\mathrm{O}\left(\theta_{m}^{4}\right) \nonumber \]

De igual manera, la expansión de la serie Taylor del integrando de\((10.30)\) viene dada por

\[\begin{aligned} \frac{1}{\sqrt{1-a^{2} \sin ^{2} \phi}} &=1+\frac{1}{2} a^{2} \sin ^{2} \phi+\mathrm{O}\left(a^{4}\right) \\ &=1+\frac{1}{8} \theta_{m}^{2} \sin ^{2} \phi+\mathrm{O}\left(\theta_{m}^{4}\right) \end{aligned} \nonumber \]

Por lo tanto, a partir de (10.30),

\[T=\frac{4}{\omega} \int_{0}^{\pi / 2} d \phi\left(1+\frac{1}{8} \theta_{m}^{2} \sin ^{2} \phi\right)+\mathrm{O}\left(\theta_{m}^{4}\right) \nonumber \]

Usando

\[\int_{0}^{\pi / 2} d \phi \sin ^{2} \phi=\frac{\pi}{4} \nonumber \]

tenemos

\[T=\frac{2 \pi}{\omega}\left(1+\frac{\theta_{m}^{2}}{16}\right)+\mathrm{O}\left(\theta_{m}^{4}\right) \nonumber \]

Solución numérica

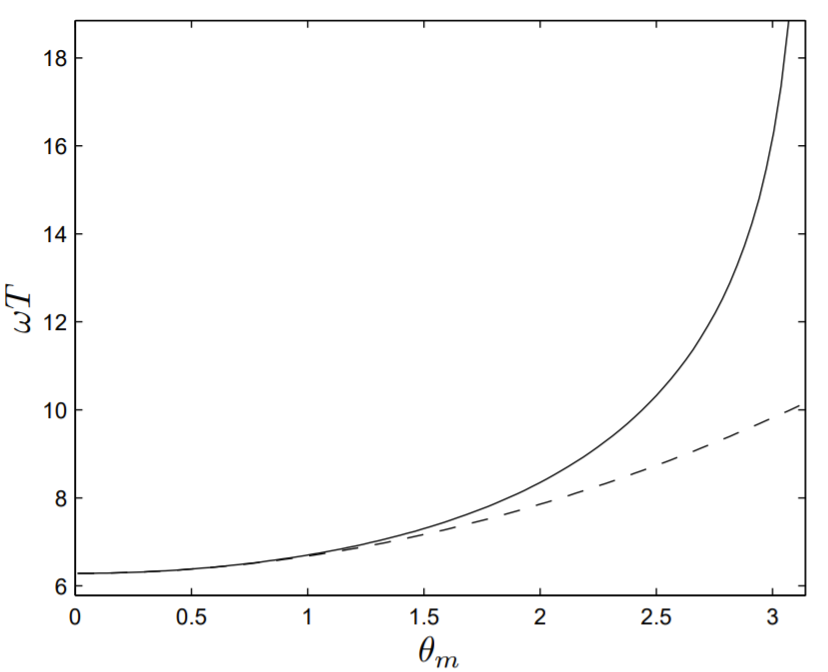
Se discuten aquí dos métodos para computar el periodo del péndulo\(T=T\left(\theta_{m}\right)\) en función de la amplitud máxima. El periodo se puede encontrar en unidades de\(\omega^{-1}\); es decir, calculamos\(\omega T\).

El primer método hace uso de nuestro trabajo analítico y realiza una integración numérica de (10.30). Los algoritmos para la integración numérica se discuten en el Capítulo 3. En particular, se puede hacer uso de la cuadratura adaptativa de Simpson, implementada en la función de MATLAB quad. \(\mathrm{m}\).

El segundo método, que es igual de razonable, resuelve directamente la ecuación diferencial (10.3). No dimensionalizar usando\(\tau=\omega t\), la ecuación\((10.3)\) se convierte en

\[\frac{d^{2} \theta}{d \tau^{2}}+\sin \theta=0 \nonumber \]

Para resolverlo\((10.35)\), escribimos esta ecuación de segundo orden como el sistema de dos ecuaciones de primer orden

\[\begin{aligned} &\frac{d \theta}{d \tau}=u, \\ &\frac{d u}{d \tau}=-\sin \theta, \end{aligned} \nonumber \]

con condiciones iniciales\(\theta(0)=\theta_{m}\) y\(u(0)=0\). Luego determinamos el tiempo (adimensional) requerido para que el péndulo se mueva a la posición\(\theta=0\): esta vez será igual a una cuarta parte del período de movimiento

Los algoritmos para la integración de ecuaciones diferenciales ordinarias se discuten\(4 .\) en Capítulo En particular, se puede hacer uso de una\((4,5)\) fórmula Runge-Kutta, el par Príncipe Dormand-Prince, que se implementa en la función de MATLAB ode\(45 . \mathrm{m}\).

Quizás la forma más sencilla de calcular el periodo es hacer uso de la propiedad Ubicación del evento del solucionador de oda MATLAB. A través de la opción odeset, es posible instruir\(45 . \mathrm{m}\) a oda para que finalice la integración de tiempo cuando\(\theta=0\) se produzca el evento, y que devuelva la hora en la que se lleva a cabo este evento.

En la Fig. 10.2\(\theta_{m}\) se muestra una gráfica del periodo adimensional\(\omega T\) versus la amplitud. Para comparación, el resultado analítico de orden bajo de\((10.34)\) se muestra como la línea discontinua.

Figura 10.2: El periodo adimensional del péndulo simple\(\omega T\) versus amplitud\(\theta_{m}\). La línea continua es el resultado numérico y la línea discontinua es una aproximación de orden bajo.