Soluciones
- Page ID
- 113192
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Módulo 1 Teoría de Conjuntos
Set de ejercicios 1 Soluciones
| a. 5P, 6P, 7P, 8P | ||||||
| b. 4D, 5D, 6D, 7D, 8D, 9D | ||||||
| c. 5H, 6H, 7H, 9H | ||||||
|
d. Hay 6 grupos. Deberías haber enumerado 2 de estos grupos:
|
5. una colección de objetos
6. los objetos en un conjunto
7. El conjunto nulo es un conjunto que no contiene elementos es decir, está vacío.
9. Sí.
| N = {4N, 5N, 6N, 7N, 8N} |
| Q = {4Q, 5Q, 6Q, 7Q, 8Q, 9Q} |
| S = {4N, 4D, 4Q} |
| W = {6P, 6N, 6D, 6Q, 6H} |
| Y = {8P, 8N, 8D, 8Q} |
| T = {} |
10.
|
a. si; cualquier elemento de N será suficiente 4N, 5N, 6N, 7N u 8N |
b. no | c. no | d. si |
11. Las respuestas pueden variar. Cualquier elemento en P será suficiente 5P, 6P, 7P o 8P
12.
| a. F | b. T | c. T | d. t | e. F |
| f. t | g. T | h. t | i. F |
| a. 4 | b. 5 | c. 6 | d. 6 | e. 3 | f. 4 |
| g. 4 | h. 0 | i. 3 | j. 5 | k. 5 | l. 5 |
| m. 25 | n. 0 | o. Z ~ S; P~H, H ~ Y; N ~ W; X ~ V; Q ~ D (no es necesario incluir subconjuntos nulos) |
15.
| a. Ø | b. {9H} | c. {4H} |
| d. {6Q} | e. Ø |
17. Dos conjuntos, A y B, son disjuntos si\(A \cap B = Ø\) es decir que su intersección está vacía.
18. 5D, 6P, 7P, 8P, 5P, 5N, 5Q, 5H. si, hay 8 monedas.
19.
| a. {4N, 5N, 6N, 7N, 8N, 4D, 4Q} |
| b. {4Q, 5Q, 6Q, 7Q, 8Q, 9Q, 6P, 6N, 6D, 6H} |
| c. {5P, 6P, 7P, 8P, 4D, 5D, 6D, 7D, 8D, 9D} |
| d. {7P, 7N, 7D, 7Q, 7H, 8P, 8N, 8D, 8Q} |
23.
| a. {2, 4} | b. {3, 5} |
| c. {} o Ø | d. {1, 2, 3, 4, 5, 6, 8} |
| e. {1, 2, 3, 4, 5, 7} | f. {2, 3, 4, 5, 6, 7, 8} |
| g. {6, 7, 8, 9} | h. {1, 3, 5, 7, 9} |
| i. {1, 2, 4, 6, 8, 9} | p. {1, 3, 5, 7} |
| j. {1, 3, 5} | q. {3, 5, 6, 7, 8, 9} |
| k. {6, 8} | r. {2,3,4,5,7} |
| l. {1, 2, 4} | s. {2, 4} |
| m. {7} | t. {6, 8, 9} |
| n. B o {2,4,6,8} | u. {7, 9} |
| o.C o {3,5,7} | v. {1, 3, 5, 6, 7, 8, 9} |
| w. {7, 9} | x. {3, 5, 6, 7, 8, 9} |
| y. t | z. |
| aa. F | bb. F |
| cc. T | dd. F |
| ee. T | f. f |
| gg. F | hh. T |
| ii. T | jj. F |
25.
| a. {a, b, c,..., z} |
| b. {124, 126, 128,..., 698} |
| c. {101, 102, 103,..., 999} |
| d. {x|x es un ex presidente de Estados Unidos hasta 1995} |
| e. {Reagan, Bush, Clinton} |
30.
| a. 3; 8; las respuestas pueden variar |
| b. 4; 6; las respuestas pueden variar |
| c. 2; 12; las respuestas pueden variar |
| d. 12; 2; las respuestas pueden variar |
| e. 8; 3; las respuestas pueden variar |
| f. 6; 4; las respuestas pueden variar |
31. e. unión
32.
| c. no |
| d. sí; LYC, LYQ, LYT |
| e. intersección; {LYC, LYQ, LYT} |
34.
| a. {} |
| b. {}, {P} |
| c. {}, {G}, {F}, {F, G} |
| d. {}, {X}, {Y}, {Z}, {X, Y}, {X, Z}, {Y, Z}, {X, Y, Z} |
| e. {}, {1}, {2}, {3}, {4}, {1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}, {1, 2, 3}, {1, 2, 4}, {1, 3, 4}, {2, 3, 4}, {1, 2, 3, 4} |
35.
| a. 1 | b. 2 | c. 4 | d. 8 |
| e. 16 | f. 32 | g.\(2^{n}\) |
36. 35
37. 35
38. si
39.
| a. bc | b.\(b^{2}\) | c.\(c^{2}\) |
40. Una posibilidad es dejar A = {m} y B = {n}. Entonces\(A \times B = {(m,n)}\) pero\(B \times A = {(n,m)}\). Por lo tanto,\(A \times B \nleq B \times A\) (asegúrese de escribir su propia solución)
41.
| a. {(3,2), (3,6), (4,2), (4,6)} |
| b. {(6,5), (7,5), (8,5), (9,5)} |
| c. {} |
| d. {(a, a)} |
| e. {(x, x), (x, y), (y, x), (y, y)} |
| f. {(1,1), (1,3), (1,5), (3,1), (3,3), (3,5), (5,1), (5,3), (5,5)} |
| g. {((9,4), D), (9,4), {a, b, c}), (C, D), (C, {a, b, c})} |
| h. {({5,6,7,8,9}, g), ({5,6,7,8,9}, {4,3})} |
Set de ejercicios 2 Soluciones
















18-56: Las respuestas a estos ejercicios son los diagramas de Venn al final del Conjunto de ejercicios 2.
Set de ejercicios 3 Soluciones
1. Las respuestas pueden variar. La superposición es la intersección. Hay 8 regiones.
2.
|
a.  |
b.  |
|
c.  |
d.  |
4.
|
a.  |
|
b.  |
|
c.  |
5. Algunas posibilidades son: triángulo, círculo, cuadrado; grande, pequeño y cualquier otro valor.
8.
|
a.  |
| b. SRT, SYT, SGT, LGT, SYC, LYT, SRC, SGC, LRT, LGC, LRC, LYC |
| c. SRT, SYT, SGT, LGT, SYC, LYT, SRC, SGC, LRT, LGC, LRC, LYC |
| d. Los elementos son exactamente los mismos |
| e.\(B \cup Q)^{c} = B^{c} \cap Q^{c}\) |
9.
|
a.  |
| b. SRT, LRQ, LRT, SRQ |
| c. SRT, LRQ, LRT, SRQ |
| d. Los elementos son exactamente los mismos. |
| e.\((R^{c} \cup C)^{c} = R \cap C^{c}\) |
10. Para las partes a y b, los sombreados finales son los mismos que se muestran en el diagrama de Venn a continuación. La ecuación que puedes escribir es:\((B \cup Q)^{c} = B^{c} \cap Q^{c}\)

11. Para las partes a y b, los sombreados finales son los mismos que se muestran en el diagrama de Venn a continuación. La ecuación que puedes escribir es:\((A \cap B)^{c} = A^{c} \cup B^{c}\)

12.
| a.\(R \cup S\) | b. (\(M^{c} \cup N^{c})^{c}\) | c.\(F^{c} \cap G\) | d.\((H \cap I^{c})^{c}\) | e.\(P \cup Q^{c}\) | f.\((S^{c} \cup T)^{c}\) |
14. Solo se proporciona una prueba a 14.c.
|
\((B^{c} \cup C)^{c} = (({2, 4, 6, 8}}}^{c} \cup {3, 5, 7}^{c}\) =\({1, 3, 5, 7, 9} \cup {3, 5, 6})^{c}\) =\(({1, 3, 5, 7, 9})^{c}\) = {2, 4, 6, 8}. |
|
\(B \cap C^{c} = {2, 4, 6, 8} \cap ({1, 3, 5, 7, 9})^{c}\) =\({2, 4, 6, 8} \cap {2, 4, 6, 8}\) = {2, 4, 6, 8}. |
Ya que\((B^{c} \cup C)^{c}\) y\(B \cap C^{C}\) tienen exactamente los mismos elementos, son iguales. Por lo tanto,\((B^{c} \cup C)^{c} = B \cap C^{c}\).
15.
|
a, b: los sombreados finales son los mismos que se muestran en el diagrama de Venn a continuación.  |
| c. {2,3,4,5} |
| d. {2,3,4,5} |
| e. Son iguales. |
16.
|
a, b: los sombreados finales son los mismos que se muestran en el diagrama de Venn a continuación.  |
| c. {1,2,3,4,5} |
| d. {1,2,3,4,5} |
| e. son lo mismo. |
17.
| a. (\(X \cap Y) \cup (X \cap Z\)) |
| b.\((P \cup Q^{c}) \cap (P \cup R\)) |
| c.\(K^{c} \cap (L \cup M)\) |
| d.\(D \cup (E^{c} \cap F\)) |
Set de ejercicios 4 Soluciones
1.
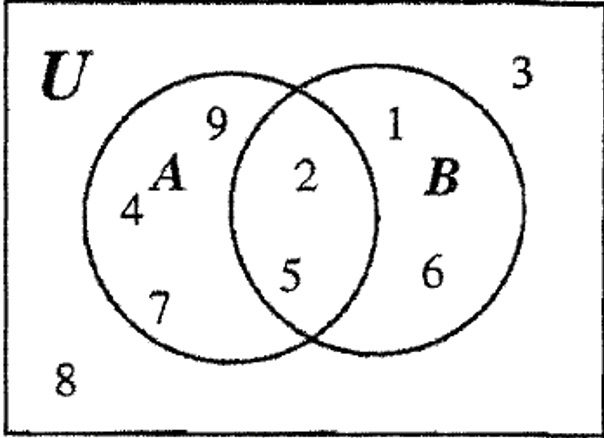
2.
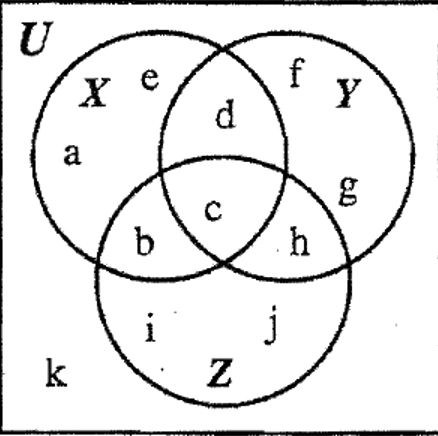
3.
| a.\((A \cup B \cup C)^{c}\) | b. A - (\(B \cup C)\) |
| c. (A\ cap B) - C | d. B - (\(A \cup C)\) |
| e.\((A \cap B \cap C\)) | f.\((A \cap C) - B\) |
| g.\((B \cap C) - A\) | h.\(C - \(A \cup B)\) |
4.
| a. 43 | b. 51 | c. 46 | d. 38 |
| e. 18 | f. 25 | g. 13 | h. 89 |
5.
| a. n (\(A - (B \cup C)\)) = 11 |
| b. n (A) = 69 |
| c. n (\(B \cap C\)) = 51 |
| d. n (\((A \cup B) - C\)) = 71 |
| e. n (\(C^{c}\)) = 73 |
| f. n (\(B \cup C\)) = 160 |
| g. n (B - C) = 60 |
| h. n (\((A \cap B) \cup (B \cap C) \cup (A \cap C)\)) = 66 |
| i. n (\((A \cap B) \cup (B \cap C) \cup (A \cap C) - (A \cap B \cap C)\)) = 23 |
6.
| a. 34 | b. 5 | c. 69 | d. 37 | e. 13 |
| f. 3 | g. 21 | h. 9 | i. 23 |
7.
|
a. 12  |
b. 2 | c. 6 |
8.
| a. 9 | b. 5 | c. 10 | d. 43 |
|
e. 37 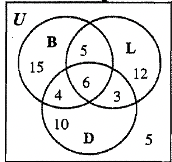 |
f. 18 | g. 3 |
9.
| a. 86 | b. 49 | c. 31 |
| d. 25 | e. 4 | f. 27 |

10. Esta es una forma de demostrarlo.

11. Esta es una forma de demostrarlo.

12. Esta es una forma de demostrarlo.

Soluciones para la tarea
1.
| a. {a, c} |
| c. {e, v, w, z} |
| e. {r, u, x} |
| g. {a, c, r, u} |
| i. {x} |
| k. Ø o {} |
| m. 10 |
| n. 2 |
3. a.\((N^{c} \cap P)^{c}\)
4. a.\(A^{c} \cup (E \cap F\))
5.
|
a.  |
| c. 15 |
| e. 5 |
| g. 9 |
6.
| a. 8 | b. 3 |
7.
| a. T | c. F | e. T |
8.
|
a.  |
c.  |
e.  |
9. a.\(A \cup (B \cap C)\)
10.
a. {}
c. {}, {a}, {b}, {a, b}
11.
| a. {(1, 1), (1, 2), (1, 4), (2, 1), (2, 2), (2, 4), (4, 1), (4, 2), (4, 4)} |
| c. {({a, c}, {a, c}), ({a, c}, 5), (5, {a, c}), (5, 5)} |
| e. {(x, x)} |
12.
| a. {LBC, LYC, LGC} |
| c. {LRC, LBC, LGC, LYC, SRC} |
Módulo 2 Conteo y Números
Set de ejercicios 1 Soluciones
8. Los conjuntos tienen el mismo número de elementos. La cardinalidad es igual.
10.
|
a) 1)\(1 \leftrightarrow A\) |
|
b. 1)\(2 \leftrightarrow B, 3 \leftrightarrow C\) 2)\(2 \leftrightarrow C, 3 \leftrightarrow B\) |
|
c. 1)\(4 leftrightarrow D, 5 leftrightarrow E, 6 leftrightarrow F\) 2)\(4 leftrightarrow D, 5 leftrightarrow F, 6 leftrightarrow E\) 3)\(4 leftrightarrow E, 5 leftrightarrow D, 6 leftrightarrow F\) 4)\(4 leftrightarrow E, 5 leftrightarrow F, 6 leftrightarrow D\) 5)\(4 leftrightarrow F, 5 leftrightarrow D, 6 leftrightarrow E\) 6)\(4 leftrightarrow F, 5 leftrightarrow E, 6 leftrightarrow D\) |
11.
|
a) 1)\(M \leftrightarrow M\) |
|
b. 1)\(x \leftrightarrow x, y \leftrightarrow z\) 2)\(x \leftrightarrow z, y \leftrightarrow x\) |
|
c. 1)\(1 \leftrightarrow 1, 2 \leftrightarrow 2\) 2)\(1 \leftrightarrow 2, 2 \leftrightarrow 1\) |
|
d. 1)\(1 \leftrightarrow 1, 2 \leftrightarrow 2, 3 \leftrightarrow 3\) 2)\(1 \leftrightarrow 1, 2 \leftrightarrow 3, 3 \leftrightarrow 2\) 3)\(1 \leftrightarrow 2, 2 \leftrightarrow 1, 3 \leftrightarrow 3\) 4)\(1 \leftrightarrow 2, 2 \leftrightarrow 3, 3 \leftrightarrow 1\) 5)\(1 \leftrightarrow 3, 2 \leftrightarrow 1, 3 \leftrightarrow 2\) 6)\(1 \leftrightarrow 3, 2 \leftrightarrow 2, 3 \leftrightarrow 1\) |
|
e. 1)\(1 \leftrightarrow 3, 2 \leftrightarrow 4, 3 \leftrightarrow 5\) 2)\(1 \leftrightarrow 3, 2 \leftrightarrow 5, 3 \leftrightarrow 4\) 3)\(1 \leftrightarrow 4, 2 \leftrightarrow 3, 3 \leftrightarrow 5\) 4) 1\ trightarrow izquierda4, 2\ izquierdatrightarrow 5, 3\ izquierdatrightarrow 3 5) 1\ izquierdatrightarrow 5, 2\ izquierdatrightarrow 3, 3\ izquierdatrightarrow 4 6) 1\ trightarrow izquierda5, 2\ izquierdatrightarrow 4, 3\ izquierdatrightarrow 3 |
12.
| a. 1 | b. 2 | c. 6 |
14.
| a. | | | | | | | | | |
| b. Hacer 512 marcas de trazo; hacer 2,000,000 marcas de trazo. |
16.
| a. | | | | | | | | | | | | | | |
|
b.  |
17. 36
18. Las respuestas pueden variar. Algunas posibilidades son hacer 123 golpes o hacer 8 I's y 53 trazos.
19.
| a. 301,020 | b. 4.010.507 |
| c. 35,000 | d. 110,023 |
20.
|
a.  |
|
b.  |
|
c.  |
|
d.  |
|
e. 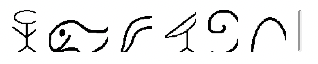 |
21. Base Diez. Sólo tienen símbolos de hasta un millón en egipcio. Esto hace que escribir números muy grandes sea demasiado engorroso y posiblemente prácticamente imposible.
24.
| a. XXXII | b. DLXI |
| c. DCCVIII | d. MMLIII |
25.
| a. 2,687 | b. 1,232 |
26.
| a.\(\bar{\text{CCCXXX}}\) DCCCII |
| b.\(\bar{\bar{\text{LXX}}}\) MDCLI |
27.
| a. CCCCCCCCCXXXXIIII o DCCCCXXXXIIII |
| b. CCCCXXXXXXXIIIIIIIIII o CCCCLXXXXVIIII |
29.
| a. DCCXLVIII |
| b.\(\bar{\text{XIV}}\) CDLXXX |
| c. CMLXIX |
| d. CDXLII |
30.
| a.\(\bar{\text{XIX}}\) CDLIII |
| b. MMDCCCXLIX |
| c. MCMXCVI |
32. 3, 1, 3, 1, 3, 1
33.
| a. 10 | b. 1 | c. 2 |
| d. 7 | e. 7 |
34.
| a. 3 |
| b. 2 |
| c. 9 |
| d. 900 golpes |
| e. 180 5 recuentados de trazos |
35.
Hindu-Árabe: 3, 3, 7, 5, 4
Carrera: 143, 400, 1000000, 30009, 2124
Cuenta: 31, 80, 200000, 6005, 428
Egipcio: 8, 4, 1, 12, 9
Romanos: 6, 2, 1, 5, 7
Set de ejercicios 2 Soluciones
1.
|
a. 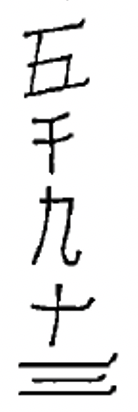 |
b.  |
c.  |
d. 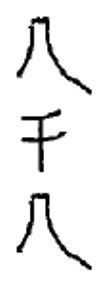 |
2.
| a. 109 | b. 6063 | c. 40 | d. 2815 | e.7800 |
3.
|
1.  |
5. 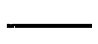 |
9.  |
13.  |
17. 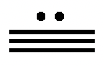 |
|
2.  |
6.  |
10.  |
14.  |
18.  |
|
3.  |
7.  |
11.  |
15.  |
|
|
4.  |
8.  |
12.  |
16.  |
19.  |
4. Un punto representa el número uno y un segmento de línea representa el número cinco. Cualquier combinación de 1-3 segmentos de línea y/o 1-4 puntos forma cualquier número hasta 19.
5.
| a. 90 | b. 320 | c. 162 |
6.
| a. 3974 | b. 1946 | c. 3300 |
| d. 32454 | e. 7319 |
7.
|
a.  |
b.  |
c.  |
d.  |
e.  |
8.
| a. 27 rem. 156 |
| b. 9 rem. 6709 |
| c. 16 rem. 13 |
| d. 2 rem. 142040 |
9. A 19 en el segundo nivel arriba es 380. A continuación se muestra el número maya para 380.

10. No se puede tener más alto que el 17 en el segundo nivel arriba porque 18 en ese nivel representa 360, que debe ser representado en el tercer nivel arriba. Para todos los demás niveles, el número más alto puede ser 19.
11.
|
a.  |
b.  |
c. 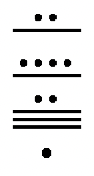
 |
d.  |
e. |
12.
|
a.  |
b.  |
c.  |
13.
| a. 10 | b. 12 | c. 3 |
14.
| Chino | Maya | |
| a. 15 |
 |
 |
| b. 100 |
 |
 |
| c. 1000 |
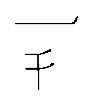 |
 |
| d. 9999 |
 |
 |
Set de ejercicios 3 Soluciones
1.
| a. 2 | b. 2 | c. 2 | d. 2 | e. 2 |
2.
| a. 27 | b. 13, 1, 14 |
| c. 6, 1, 1, 8 | d. 3, 0, 1, 1, 5 |
| e. 1, 1, 0, 1, 1, 4 | f. 1, 1, 0, 1, 1 |
| g. 27, 4 |
3.
| a. 18 | b. 9, 0, 9 |
| c. 4, 1, 0, 5 | d. 2, 0, 1, 0, 3 |
| e. 1, 0, 0, 1, 0, 2 | f. 1, 0, 0, 1, 0 |
4.
| a. 45 | b. 22, 1, 23 |
| c. 11, 0, 1, 12 | d. 5, 1, 0, 1, 7 |
| e. 2, 1, 1, 0, 1, 5 | |
| f. 1, 0, 1, 1, 0, 1, 4 | |
| g. 1, 0, 1, 1, 0, 1 |
5.
| a. tres, cero, dos, base seis |
| b. uno, cero, uno, uno, base dos |
| c. cuatro, tres, cinco, base siete |
6.
| a.\(5016_{\text{eight}}\) | b.\(101001_{\text{two}}\) |
7.
| 2048, 1024, 512, 256,... |
8.
| a. 19 | b. 65 | c. 63 |
9. 3125, 625, 125, 25, 5, 1
10. 8
11. 2187, 729, 243, 81, 27, 9, 3, 1
12.
| a. 500 | b. 3711 | c. 1093 |
13.
| a. Seis: 7776, 1296, 216, 36, 6, 1 |
| b. siete: 16807, 2401, 343, 49, 7, 1 |
| c. Nueve: 59049, 6561, 729, 81, 9, 1 |
| d. ocho: 32768, 4096, 512, 64, 8, 1 |
| e. Cuatro: 1024, 256, 64, 16, 4, 1 |
| f. diez: 100000,10000,1000,100,10,1 |
| g. Doce: 20736, 1728, 144, 12, 1 |
| h. Once: 14641, 1331, 121, 11, 1 |
14. \(n^{10}, n^{9}, n^{8}, n^{6}, n^{5}, n^{4}, n^{2}, n^{1}\)
15.
| a.\(3 \times 815 + 6 \times 811 + 2 \times 87\) |
| b.\(3 \times 515 + 4 \times 510 + 2 \times 57\) |
| c.\(4 \times 1114 + 3 \times 1110 + 2 \times 110\) |
| d.\(1 \times 214 + 1 \times 211 + 1 \times 24\) |
16.
| a.\(9^{6}\) | b.\(9^{0}\) | c.\(9^{12}\) | d.\(9^{10}\) |
17.
| a.\(2401000300_{\text{five}}\) |
| b.\(30040001600_{\text{eight}}\) |
| c.\(7000804000_{\text{twelve}}\) |
| d.\(201010200_{\text{three}}\) |
18.
| a.\(6^{17}\) | b.\(9^{19}\) |
19. 3:0, 1, 2
20. 4:0, 1, 2, 3
21. 5:0, 1, 2, 3, 4
22. 6:0, 1, 2, 3, 4, 5
23. 8:0, 1, 2, 3, 4, 5, 6, 7
24. No, porque los únicos dígitos que pueden aparecer en un número Base Siete son 0, 1, 2, 3, 4, 5 y 6.
25.
| a. Siete |
| b. No hay base más alta, puede ocurrir en cualquier base superior a Seis. |
26. 11
27. 12
28. 13
29.
| a. 671 | b. 1291 | c. 1830 |
| d. 3496 | e. 1358 | f. 2231 |
30.
| a. 6 | b. 12 | c. 20 | d. 30 |
| e. 42 | f. 56 | g. 72 | h. 90 |
| i. 132 | j. 156 | k. 182 | l. 420 |
31. \(13201154320050146_{\text{eleven}}\)es más grande. El ejercicio 30 ilustra que si dos números tienen los mismos dígitos exactos, el que tiene la base más alta tiene un valor mayor ya que cada valor posicional vale más. Las explicaciones pueden variar.
32. \(4 \times 1213 + 10 \times 129 + 11 \times 123\)
33. \(600T000E0000W00_{\text{thirteen}}\)
Set de ejercicios 4 Soluciones
1. Pregúntale a un amigo cómo es tu obra de arte.
2.
| a. 4, 4, 4, 4, 4, 4 |
| b. 4,16,64,256 |
| c. 5 |
| d. 36 |
3. 2, 2, 2, 2, 2
4. 3, 3, 3
5. 4, 4, 4
6.a.
|
i. 42 ii. 21, 0 iii. 10, 1, 0 iv. 5, 0, 1, 0 v. 2, 1, 0, 1, 0 vi. 1, 0, 1, 0, 1, 0 vii. Ver primera fila de la parte d. |
| b. Ver segunda fila de la parte d. |
| c. Véase tercera fila de la parte d. |
|
d. 101010 Base Dos 001120 Base Tres 000222 Base Cuatro |
7.
| a.\(110100_{\text{two}}\) |
| b.\(1221_{\text{three}}\) |
| c.\(310_{\text{four}}\) |
8.
| a.\(3020_{\text{four}}\) |
| b.\(1212_{\text{seven}}\) |
| c.\(1011001_{\text{two}}\) |
| d.\(100210_{\text{three}}\) |
| e.\(1E8_{\text{thirteen}}\) |
9.
| a.\(12202_{\text{three}}\) |
| b.\(10E_{\text{twelve}}\) |
| c.\(10011011_{\text{two}}\) |
| d.\(1110_{\text{five}}\) |
10.
| a.\(T23T_{\text{eleven}}\) |
| b.\(625T_{\text{thirteen}}\) |
11.
| a.\(59T_{\text{twelve}}\) |
| b.\(1506_{\text{eight}}\) |
| c.\(2305_{\text{seven}}\) |
| d.\(1131_{\text{nine}}\) |
13. 10
14. El último dígito del número anterior debe haber sido un 9 y el último dígito del nuevo número será 0.
15. 99,999,999
16. 1,000,000,000
17. 3
18. El último dígito del número anterior debe haber sido un 2 y el último dígito del nuevo número será 0.
19. \(1000000_{\text{three}}\)
20. \(2222222_{\text{three}}\)
21.
| a.\(1202011_{\text{three}}\) |
| b.\(2220012_{\text{three}}\) |
| c.\(1010110_{\text{three}}\) |
| d.\(2100220_{\text{three}}\) |
| e.\(2121000_{\text{three}}\) |
22.
| a.\(1200101_{\text{three}}\) |
| b.\(1202220_{\text{three}}\) |
| c.\(2110012_{\text{three}}\) |
| d.\(2110022_{\text{three}}\) |
23. El dígito “3" no puede estar en el numeral.
24. \(0_{\text{four}}, 1_{\text{four}}, 2_{\text{four}}, 3_{\text{four}}, 10_{\text{four}}, 11_{\text{four}}, 12_{\text{four}}, 13_{\text{four}}, 20_{\text{four}}, 21_{\text{four}}, 22_{\text{four}}, 23_{\text{four}}, 30_{\text{four}}, 31_{\text{four}}, 32_{\text{four}}, 33_{\text{four}}, 100_{\text{four}}, 101_{\text{four}}, 102_{\text{four}}, 103_{\text{four}}, 110_{\text{four}}, 111_{\text{four}}, 112_{\text{four}}, 113_{\text{four}}\)
25. 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111, 10000, 10001, 10010, 10011, 10100
26. 75, 76, 77, 100, 101, 102, 103, 104
27.
| a.\(3026_{\text{eight}}, 3030_{\text{eight}}\) |
| b.\(1234_{\text{five}}, 1241_{\text{five}}\) |
| c.\(101011_{\text{two}}, 101101_{\text{two}}\) |
28.
| a.\(12221_{\text{three}}\), 160 |
| b.\(2405_{\text{eight}}\), 1285 |
| c.\(1310_{\text{three}}\), 205 |
Set de ejercicios 5 Soluciones
1.
| a.\(\frac{1}{4}\) | b.\(\frac{1}{16}\) | c.\(\frac{1}{64}\) |
| d.\(\frac{1}{3}\) | e.\(\frac{1}{25}\) | f.\(\frac{1}{8}\) |
2.
| a. 35\(\frac{1}{4}\) | b. 168\(\frac{7}{11}\) |
| c. 15\(\frac{1}{2}\) | d. 27\(\frac{1}{2}\) |
3.
| a. 27\(\frac{13}{36}\) | b. 45\(\frac{27}{64}\) |
| c. 90\(\frac{9}{49}\) | d. 7\(\frac{5}{8}\) |
| e. 26\(\frac{26}{27}\) | f. 1475\(\frac{5}{72}\) |
4.
| a. binario: 00110101; decimal: 53 |
| b. binario: 10011010; decimal: 154 |
| c. binario: 01010100; decimal: 84 |
| d. binario: 00000000; decimal: 0 |
| e. binario: 11111111; decimal: 255 |
5.
| a. binario: 00110101; hex: 35 |
| b. binario: 10011010; hex: 9A |
| c. binario: 01010100; hex: 54 |
| d. binario: 00000000; hexadecimal: 00 |
| e. binario: 11111111; hex: FF |
6.
| a. binario: 01011110; decimal: 94 |
| b. binario: 11100101; decimal: 229 |
| c. binario: 00111001; decimal: 57 |
| d. binario: 00011111; decimal: 31 |
| e. binario: 10011000; decimal: 152 |
| f. binario: 00101010; decimal: 42 |
| g. binario: 00000111; decimal: 7 |
| h. binario: 01000000; decimal: 64 |
7.
| a. me encantan las matemáticas! |
| b. ¡Enseñar es una carrera desafiante pero gratificante! |
8.
|
a. Hex: 48, 45, 4C, 50, 21 Binario: 01001000,01000101, 01001100, 01010000, 00100001 |
|
b. hex.: 2,45,20,48,41,50,50,59,2E Binario: 01000010, 01000101,00100000,01000,01000,01000001,01010000, 01010000, 01011001, 00101110 |
| c. ¡Esto dependerá de tu nombre! |
9.
| a. binario:\(1001001_{\text{two}}\) hexadecimal:\(49_{\text{sixteen}}\) |
| b. binario:\(1111010_{\text{two}}\) hexadecimal:\(7A_{\text{sixteen}}\) |
| c. binario:\(110010_{\text{two}}\) hexadecimal:\(32_{\text{sixteen}}\) |
| d. binario:\(11111010_{\text{two}}\) hexadecimal:\(FA_{\text{sixteen}}\) |
| e. binario:\(1111101000_{\text{two}}\) hexadecimal:\(3E8_{\text{sixteen}}\) |
Soluciones para la tarea
1. b. No hay coincidencia posible porque la cardinalidad de los dos conjuntos es diferente
2. Una posibilidad es:\(1 \leftrightarrow 5, 2 \leftrightarrow 10, 3 \leftrightarrow 15, 4 \leftrightarrow 20\), etc. dar su propia respuesta
3.
(1)\(SBC \leftrightarrow SRC, SBT \leftrightarrow SRT, SBQ \leftrightarrow SRQ\)
(2)\(SBC\leftrightarrow SRC, SBT \leftrightarrow SRQ, SBQ \leftrightarrow SRT\)
(3)\(SBC \leftrightarrow SRT, SBT \leftrightarrow SRC, SBQ \leftrightarrow SRQ\)
(4)\(SBC \leftrightarrow SRT, SBT \leftrightarrow SRQ, SBQ \leftrightarrow SRC\)
(5)\(SBC \leftrightarrow SRQ, SBT \leftrightarrow SRT, SBQ \leftrightarrow SRC\)
(6)\(SBC \leftrightarrow SRQ, SBT \leftrightarrow SRC, SBQ \leftrightarrow SRT\)
4.
| a. 16 |
| c. 1962 |
| d. 744 |
| f. 3,031,020 |
| h. 50,703 |
| i. 1395 |
| k. 971 |
5.
| a. CCCXLII |
|
c.  |
|
e. 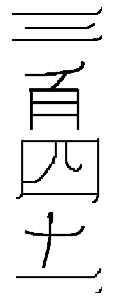 |
6.
| a.\(59T_{\text{twelve}}\) |
d. 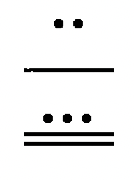 |
7. \(7T4E_{\text{twelve}}\)
10. a.\(17342575T_{\text{eleven}}\)
11. a.\(539100E0_{\text{twelve}}\)
13.
| a.\(10122_{\text{three}}\) | b. 98 |
14.
| a.\(300640000_{\text{seven}}\) | c.\(40T00E00_{\text{thirteen}}\) |
15.
| a.\(2 \times 911 + 5 \times 97 + 3 \times 94\) | c.\(8 \times 1210 + 11 \times 125 + 10 \times 123\) |
16.
| a.\(39\frac{1}{3}\) | b.\(16\frac{7}{9}\) |
18.
| a.\(302.301_{\text{four}}\) | c.\(101.1001_{\text{two}}\) |
Módulo 3 Suma y Resta
Set de ejercicios 1 Soluciones
1.
| b. 3 | d. 4 | f. 7 |
2.
| a. {t, u, v, w, x, y, z} | b. 7 | c. no | d. no | e. A & B no deben tener elementos en común. |
4.
| a. {LBT, LBC, LBQ, LRT, LRC, LRQ, LGT, LGQ, LGC, LYT, LYC, LYQ, SBT, SRT, SGT, SYT} | b. 16 | c. no | d. L y T tienen elementos en común. |
5.
|
a. Que A = {x, y} y B = {a, b, c, d} 2+4 = n (A) + n (B) =\(n(A \cup B)\) = n ({x, y, a, b, c, d}) = 6 Por lo tanto, 2 + 6 = 6 |
Dado que n (A) = 2, n (B) =4\(A \cap B =Ø\), y, luego sustituyendo n (A) por 2 y n (B) por 4 sustituyendo n (A) por 2 y n (B) por 4\(A \cup B\) calculando contando los elementos en\(A \cup B\) |
|
b. Que A = {x, y} y B = {a, b} 2+2 = n (A) +n (B) =\(n(A \cup B)\) = n ({x, y, a, b}) = 4 Por lo tanto, 2 + 2 = 4 |
Dado que n (A) = 2, n (B) =2, y\(A \cap B = Ø\), luego sustituyendo n (A) por 2 y n (B) por 2 por la teoría de conjuntos definición de suma\(A \cup B\) calculando contando los elementos en\(A \cup B\) |
|
c. Que A = {x, y, z} y B = {} 3 + 0 = n (A) + n (B) =\(n(A \cup B)\) = n ({x, y, z}) = 3 Por lo tanto, 3 + 0 = 3 |
Dado que n (A) = 3, n (B) =0, y\(A \cap B = Ø\), luego sustituyendo n (A) por 3 y n (B) por 0 por la teoría de conjuntos definición de suma\(A \cup B\) calculando contando los elementos en\(A \cup B\) |
6.
| a. K | b. h | c. B | d. o | e. S |
| f. p | g. B | h. n | i. H | j. b |
| k. n | l. | m. cada par es igual. |
8.
| a. Y, B | b. D, B | c. mismo | d. B, S | e. D, S | f. mismo |
11.
| a. Propiedad conmutativa de adición |
| b. Propiedad conmutativa de adición |
| c. Propiedad asociativa de adición |
| d. Propiedad asociativa de adición |
13. W + W + W, W + R, R + W, L
14. 1 + 1 + 1 = 3, 1 + 2 = 3, 2 + 1 = 3, 3 = 3
15. P, W + W + W + W, W + W + R, W + R + W, R + W + W, W + L, L + W, R + R
16. 4 = 4, 1 + 1 + 1 + 1 = 4, 1 + 3 = 4, 3 + 1 = 4, 2 + 2 = 4, 1 + 1 + 2 = 4, 1 + 2 + 1 = 4, 2 + 1 + 1 = 4
17. Hay once trenes: R + P, L+ L, R + R + R, W + W + W + L, D, W + W + W + W + W + W + W + W + W + W + W + W + R, W + W + W + R, W + W + P, W + W + R + R
18. 1 + 1 + 1 + 1 + 1 + 1 = 6, 1 + 5 = 6, 1 + 1 + 4 = 6, 1 + 1 + 1 + 1 + 2 = 6, 1 + 1 + 2 + 2 = 6, 1 + 1 + 3 = 6, 6 = 6, 2 + 2 + 2 = 6, 1 + 2 + 3 = 6, 3 + 3 = 6, 2 + 4 = 6
19.
| a. R | b. y | c. N |
| d. r | e. P | f. w |
20.
| b. porque 30 = 22 + 8 |
| c. porque 156 = 96 + 60 |
| d. porque 80 = 0 + 80 |
| e. porque 231 = 195 + 36 |
| f. porque 987 = 967 + 20 |
21.
| b. porque 30 + 69 = 99 |
| c. porque 19 + 51 = 70 |
| d. porque 0 + 32 = 32 |
| e. porque 489 + 11 = 500 |
| f. porque 65 + 136 = 201 |
22.
| a. izquierda | b. derecha |
23. si
24. si
25.
| a. < | b. > |
26. {0, 1, 2, 3,.}
27. si
28. no
29.
| a. cerrado (desde 0 + 0 = 0) |
| b. no cerrado; 1 + 1 = 2 es un contraejemplo |
| c. cerrado; mult de 2: ¡te queda prueba! |
| d. no cerrado; 1 + 3 = 4 es un contraejemplo |
Set de ejercicios 2 Soluciones
1.
|
a.  |
|
b.  |
|
c.  |
|
d.  |
2.
| a. B | b. d | c. G |
3.
| a. DDDCCCCCCCAAAAA |
| b. EEEDCCCCCBBAAAA |
| c. FEB |
| d. e |
4.
|
a.  |
b.  |
c.  |
5.
|
a.  |
b.  |
c.  |
|
d.  |
e.  |
6. \(33_{\text{four}} + 31_{\text{four}} = 130_{\text{four}}\)
7. \(21_{\text{seven}} + 16_{\text{seven}} = 40_{\text{seven}}\)
8. \(1111_{\text{two} + 1101_{\text{two} = 11100_{\text{two}}\)
9. \(16_{\text{nine}} + 14_{\text{nine}} = 31_{\text{nine}}\)
10. \(120_{\text{three}} + 111_{\text{three}} = 1001_{\text{three}}\)
11. \(17_{\text{eight}} + 15_{\text{eight}} = 34_{\text{eight}}\)
13.
| a.\(2_{\text{nine}}\) | b.\(2_{\text{seven}}\) | c.\(T_{\text{twelve}}\) |
| d.\(8_{\text{eleven}}\) | e.\(4_{\text{six}}\) | f.\(1_{\text{two}}\) |
| g.\(1_{\text{three}}\) | h.\(3_{\text{four}}\) | i.\(2_{\text{five}}\) |
14.
| a.\(14_{\text{eleven}}\) | b.\(12_{\text{five}}\) |
| c.\(11_{\text{eight}}\) | d.\(11_{\text{thirteen}}\) |
| e.\(12_{\text{four}}\) | f.\(13_{\text{seven}}\) |
| g.\(11_{\text{three}}\) | h.\(10_{\text{two}}\) |
| i.\(12_{\text{six}}\) | j.\(13_{\text{nine}}\) |
15.
|
a. Mesa de Adición Base Tres  |
|
b. Tabla de Adición Base Seis  |
|
c. Tabla de Adición Base Dos 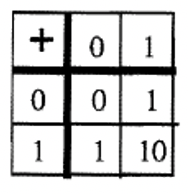 |
Set de ejercicios 3 Soluciones
1.
| a. 50 | b. 51 | c. 47 | d. 52 |
2.
| a. 69 | b. 70 | c. 74 |
3.
| a. 47 | b. 43 | c. 53 | d. 53 |
4.
| a.\(1065_{\text{thirteen}}\) | b.\(10110_{\text{two}}\) |
| c.\(12222_{\text{five}}\) | d.\(1168_{\text{nine}}\) |
| e.\(110100_{\text{two}}\) | f.\(10211_{\text{three}}\) |
| g.\(T450_{\text{twelve}}\) | h.\(11521_{\text{seven}}\) |
6.
|
a. 43 + 47 = (40 + 3) + (40 + 7) = (40 + 40) + (3 + 7) = 80 + 10 = 90 |
|
b. 88 + 54 = (80 + 8) + (50 + 4) = (80 + 50) + (8 + 4) = 130 + 12 = 100 + 30 + 10 + 2 = 100 + 40 + 2 = 142 |
7. El primer alumno suma las unas (9 + 7 = 16), luego las decenas (50 + 60 = 110) y en tercer lugar, las centenas (800 + 400 = 1200). A continuación se suman esas tres sumas intermedias (16 + 110 + 1200 = 1326). El segundo alumno está haciendo básicamente lo mismo excepto que primero se agregan los cientos, luego se agregan las decenas y unas. El primer alumno está agregando de derecha a izquierda mientras que el segundo estudiante está agregando de izquierda a derecha.
9.
| a. 12,109 | b. 111,463 |
| c. 16,668 | d. 128,334 |
10.
| a. 8,805 | b. 10,463 |
| c. 13,029 | d. 106,003 |
11.
| a.\(1300_{\text{six}}\) | b.\(1392_{\text{eleven}}\) |
| c.\(1166_{\text{eight}}\) | d.\(11001_{\text{two}}\) |
| e.\(3201_{\text{five}}\) | f.\(1065_{\text{thirteen}}\) |
| g.\(10110_{\text{two}}\) | h.\(12222_{\text{five}}\) |
| i.\(1168_{\text{nine}}\) | j.\(110100_{\text{two}}\) |
| k.\(10211_{\text{three}}\) | l.\(T450_{\text{twelve}}\) |
| m.\(11521_{\text{seven}}\) |
12.
| a. siete |
| b. trece |
| c. doce |
| d. tres - trece |
| e. cuatro - trece |
13.
| a. Base Ocho;\(132_{\text{eight}}\) |
| b. Base Nueve:\(82_{\text{nine}}\) |
| c. Base Tres;\(110_{\text{three}}\) |
| d. Base Diez; 123 |
14. Ella pensó en 68 como 70 - 2. Entonces, 47 + (70 - 2) = (47 + 70) - 2 = 117 - 2 = 15
15. Primero, sumó las decenas juntas, (40 + 60 = 100), luego sumó las juntas (8 + 7 = 15) y finalmente sumó las dos sumas preliminares juntas (100 + 15 = 115).
18. 1115; CELOSÍA MOSTRADA A CONTINUACIÓN

19.
|
a.\(41_{\text{six}}\)  |
b.\(WOE_{\text{thirteen}}\)  |
20. Estimación: $46; Suma Real: $45.18
22. Subestimarás si por casualidad redondear hacia abajo en casi todos los artículos. Sobestimarás si por casualidad redondear casi todos los artículos.
Set de ejercicios 4 Soluciones
2.
| a. 7 | b. 3 | c. 4 |
4.
|
a. dejar A = {t, u, v, w, x, y, z} y B = {w, y, z}. Dado que n (A) = 7, n (B) = 3 y\(B \subseteq A\), 7 - 3 = n (A) - n (B) sustituyendo n (A) por 7 y n (B) por 3 = n (A\ B) por la teoría de conjuntos definición de sustitución = n ({t, u, v, x}) calculando A\ B = 4 contando los elementos en A\ B Por lo tanto, 7 - 3 = 4. |
|
a. dejar A = {t, u, v, w, x, y, z} y B = {w, y, z}. Dado que n (A) = 7, n (B) = 3 y\(B \subseteq A\), 7 - 3 = n (A) - n (B) sustituyendo n (A) por 7 y n (B) por 3 = n (A\ B) por la teoría de conjuntos definición de sustitución = n ({t, u, v, x}) calculando A\ B = 4 contando los elementos en A\ B Por lo tanto, 7 - 3 = 4. |
|
a. dejar A = {t, u, v, w, x, y, z} y B = {w, y, z}. Dado que n (A) = 7, n (B) = 3 y\(B \subseteq A\), 7 - 3 = n (A) - n (B) sustituyendo n (A) por 7 y n (B) por 3 = n (A\ B) por la teoría de conjuntos definición de sustitución = n ({t, u, v, x}) calculando A\ B = 4 contando los elementos en A\ B Por lo tanto, 7 - 3 = 4. |
5.
|
a.  |
b.  |
6.

7.
|
a.  |
b.  |
|
c.  |
d.  |
8.
| \(32_{\text{five}}; 14_{\text{five}}; 13_{\text{five}}\) \(32_{\text{five}} – 14_{\text{five}} = 13_{\text{five}}\) |
9.
| \(21_{\text{eight}}; 7_{\text{eight}}; 12_{\text{eight}}\) \(21_{\text{eight}} – 7_{\text{eight}} = 12_{\text{eight}}\) |
10.
| \(210_{\text{three}}; 21_{\text{three}}; 112_{\text{three}}\) \(210_{\text{three}} – 21_{\text{three}} = 112_{\text{three}}\) |
12. L
13.
| a. B | b. y | c. N | d. n | e. |
14. Esto se hace con las C-Sstrips.
15. No; 7 —10 no es un número entero
16.
| a. cerrado | b. no cerrado; 2-4 es un contraejemplo |
17.
| a. 12 — 4 = 8; 12 — 8 = 4 |
| b. 170 — 130 = 40; 170 — 40 = 130 |
| c. 80 — 62 = 18; 80 — 18 = 62 |
18.
| a. 4 = 7 —3 | b. 8 = 9 —1 |
19. No. 4 < 7 pero no es cierto que 7 < 4
21.
| a. 2; 9 = 7 + 2 | b. 7; 13 = 6 + 7 |
| c. 80; 88 = 8 + 80 | d. 56; 70 = 14 + 56 |
22. \(41_{\text{five}}\)
23. \(1_{\text{two}}\)
24. \(4E_{\text{twelve}}\)
25.
| a. -5 | b. 3 |
26.
|
a. 6 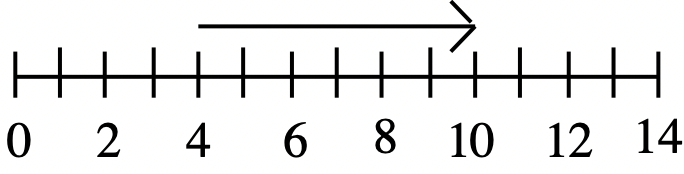 |
|
b. 7 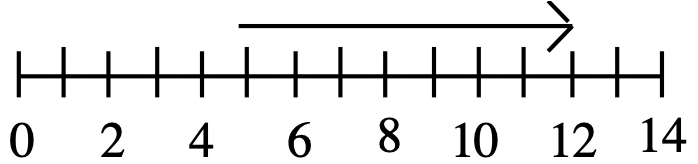 |
|
c. 5  |
|
d. 2 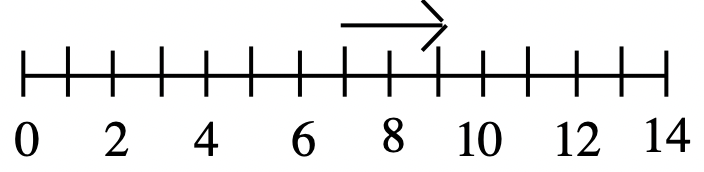 |
|
e. -7  |
|
f. -3  |
|
g. -12  |
|
h. 0  |
27. vector a: 6; vector c: -5; vector d: 3
Set de ejercicios 5 Soluciones
1.
| a.\(314_{\text{thirteen}}\) | b.\(151_{\text{nine}}\) |
| c.\(1225_{\text{six}}\) | d.\(134_{\text{five}}\) |
| e.\(12_{\text{three}}\) |
2.
| a. 1618 | b.\(31_{\text{four}}\) |
| c.\(363_{\text{twelve}}\) | d.\(45_{\text{six}}\) |
| e.\(111_{\text{two}}\) | f.\(254_{\text{nine}}\) |
| g.\(33_{\text{five}}\) | h.\(234_{\text{seven}}\) |
| i.\(2_{\text{three}}\) | j.\(236_{\text{eight}}\) |
3. Muestre el cheque sumando la respuesta al sustraendo y asegurándose de que la suma sea el minuendo.
4.
| a. 6717 | b.\(1214_{\text{five}}\) |
| c.\(1424_{\text{eight}}\) | d.\(49E_{\text{thirteen}}\) |
| e.\(1010_{\text{two}}\) |
5. Muestre la comprobación sumando la diferencia (respuesta) al sustraendo y asegurándose de que la suma es el minuendo.
6.
| a. 6697 | b.\(1144_{\text{five}}\) |
| c.\(1774_{\text{eight}}\) | d.\(4WE_{\text{thirteen}}\) |
| e.\(111_{\text{two}}\) |
7. Muestre la comprobación sumando la diferencia (respuesta) al sustraendo y asegurándose de que la suma es el minuendo.
10.
| a. 9462 | b.\(122_{\text{four}}\) | c.\(101_{\text{two}}\) |
11. \(1_{\text{two}}\)
12.
| a. 4677 | b.\(134_{\text{five}}\) |
13.
| a. Dado que el minuendo es\(120_{\text{three}}\), el siguiente bloque de valor posicional es un bloque base tres. Ya que lo es el sustraendo\(12_{\text{three}}\), tenemos que averiguar a qué añadir\(12_{\text{three}}\) para hacer un bloque. \(12_{\text{three}}\)es una larga y dos unidades, así que tengo que agregar 1 unidad, 1 larga y 2 pisos para hacer un bloque. Por lo tanto, culo 2 pisos, un largo una unidad al minuend,\(120_{\text{three}}\), lo que da 1 cuadra, 1 plana y 1 unidad para el nuevo minuend. Si quito el bloque más grande de este nuevo minuend, debería tener la respuesta de 1 piso y 1 unidad.Entonces la respuesta es\(101_{\text{three}}\). Te he dejado el dibujo a ti. Ver #13 a continuación para ver cómo iniciar el problema con un dibujo abreviado. |
|
b. Dado que el minuendo es\(213_{\text{four}}\), el siguiente bloque de valor posicional es un bloque base cuatro. Ya que lo es el sustraendo\(133_{\text{four}}\), tenemos que averiguar a qué añadir\(133_{\text{four}}\) para hacer un bloque. \(133_{\text{four}}\)es un piso, 3 largos y tres unidades, así que tengo que agregar 1 unidad y 2 pisos para hacer un bloque. Por lo tanto, agregar 2 pisos y una unidad al minuendo\(213_{\text{four}}\), lo que da 1 cuadra y 2 largos para el nuevo minuendo. Si quito el bloque más grande de este nuevo minuendo, debería tener la respuesta de 2 largos. Entonces la respuesta es\(20_{\text{four}}\). Puede usar abreviaturas para el dibujo y comenzar representando cada número original como se muestra a continuación. He dejado la parte para sumar y resta final para ti  |
14.
| a. está dividiendo el sustraendo en tres partes (100 + 50 + 2), restando un valor posicional a la vez. 634 — 100 = 534; 534 — 50 = 484; 484 — 2 =482. |
| b. Está utilizando un método complementario. Si agregas 48 a 152, obtienes 200. Por lo que suma 48 al minuendo (634 + 48 = 682) y luego resta 200. |
Soluciones para la tarea
1. Proporcione sus propios conjuntos. Aquí hay una solución.
a. primero, debemos definir dos conjuntos, A y B, que sean disjuntos entre sí, de tal manera que un conjunto tenga 5 elementos y el otro tenga 3 elementos.
Sea A = {1, 2, 3, 4, 5} y B = {x, y, z}. Dado que n (A) = 5, n (B) = 3 y\(A \cap B = Ø\), podemos encontrar la suma de 5 y 3 formando primero la unión de A y B y luego contando el número de elementos en su unión. \(A \cup B\)= {1, 2, 3, 4, 5, x, y, z}. Desde n (\(A \cup B\)) = 8, entonces 5 + 3 = 8.
2. a. desde 79 = 66 + 13
3. a. cerrado bajo ambas operaciones
4.
|
a.  |
|
c.  |
5.
|
a.  |
|
c.  |
6.
| a.\(12325_{\text{six}}\) | b.\(2535_{\text{five}}\) |
13. a. 6

14.
| a. Base 9 |
| c. Bases Tres a Trece |
Módulo 4 Multipication
Set de ejercicios 1 Soluciones
1.
|
b. Paso 1:  |
Paso 2:  |
c. Paso 3:  |
d. ambos trenes tienen la misma longitud |
2.
| a. 2 verde oscuro | b. 6 rojo | c. 12, 12 | d. misma longitud | e.\(R \times D = D \times R ; 2 \times 6 = 6 \times 2\) |
3.
| a. 7 verde claro | b. 3 negro | c. 21, 21 | d. misma longitud | e.\(K \times L = L \times K ; 7 \times 3 = 3 \times 7\) |
4.
| a. 12 blanco | b. 1 rosa intenso | c. 12, 12 | d. misma longitud | e.\(H \times W = W \times H ; 12 \times 1 = 1 \times 12\) |
5.
| a. D | b. W | c. R | d. p | e. L | f. K | g. l | h. de R | i. R |
6.
|
a. Estos son los cuatro trenes, pero es posible que los hayan catalogado en un orden diferente.  |
|
b. Utilizando los trenes indicados anteriormente, Tren 1:\(R \times D = H\), o\(2 \times 6 = 12\) Tren 2:\(P \times L = H\), o\(4 \times 3 = 12\) Tren 3:\(D \times R = H\), o\(6 \times 2 = 12\) Tren 4:\(H \times W = H\), o\(12 \times 1 = 12\) |
7. Rojo, R
8.
| a. 3 + 3 + 3 + 3 + 3 + 3 = 18 |
| b. 9 + 9 = 18 |
| c. 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 = 18 |
9.
| a.\(4 \times 3 = 3 + 3 + 3 + 3 = 6 + 3 + 3 = 9 + 3 = 12 ; 3 \times 4 = 4 + 4 + 4 = 8 + 4 = 12\) |
| b.\(2_{\text{five}} \times 3_{\text{five}} = 3_{\text{five}} + 3_{\text{five}} = 11_{\text{five}} ; 3_{\text{five}} \times 2_{\text{five}} = 2_{\text{five}} + 2_{\text{five}} + 2_{\text{five}} = 11_{\text{five}}\) |
10. Solo se muestra la respuesta, y no los pasos individuales
|
a.  |
|
b.  |
|
c.  |
11.
|
b.  |
c. 6 |
|
e.  |
f. 6 |
| g. misma longitud | h. (\(R \times L ) \times P) = R \times (L \times P)\) |
| i.\((2 \cdots 3) \cdots 4 = 2 \cdots (3 \cdots 4)\) | j.\((2 \cdots 3) \cdots 4 = 6 \cdots 4 = 24; 2 \cdots (3 \cdots 4) = 2 \cdots 12 = 24\) |
| k. si |
12.
|
b.  |
c. 10 |
|
e.  |
f. 10 |
| g. misma longitud | h.\((Y \times R ) \times L) = Y \times (R \times L)\) |
| i.\((5 \cdots 2) \cdots 3 = 5 \cdots (2 \cdots 3)\) | j.\((5 \cdots 2) \cdots 3 = 10 \cdots 3 = 30; 5 \cdots (2 \cdots 3) = 5 \cdots 6 = 30\) |
| k. si |
13. Hacer el orden de las operaciones para simplificar cada lado de cada ecuación en a - d.
14. Hay varias combinaciones que podrías usar para la parte a.
15.
| a. 3 tiras moradas y 3 tiras amarillas. | b. lo mismo que la parte a |
| c.\(L \times (P + Y) = (L \times P) + (L \times Y)\) | d.\(4 \times (2 + 3) = (4 \times 2) + (4 \times 3)\) |
| e.\(4 \times (2 + 3) = 4 \times 5 = 20\) y\((4 \times 2) + (4 \times 3) = 8 + 12 = 20\) |
16.
| a. 2 tiras blancas y 2 tiras verde oscuro | b. lo mismo que la parte a |
| c.\(R \times (W + D) = (R \times W) + (R \times D)\) | d.\(2 \times (1 + 6) = (2 \times 1) + (2 \times 6)\) |
| e.\(2 \times (1 + 6) = 2 \times 7 = 14\) y\((2 \times 1) + (2 \times 6) = 2 + 12 = 14\) |
17. Hacer el orden de las operaciones para simplificar cada lado de cada ecuación en a - d.
18. Hay varias combinaciones que podrías usar para las partes a y b.
19.
| a. R;\(1 \cdots 2 = 2\) | b. B;\(1 \cdots 9 = 9\) | c. D;\(1 \cdots 6 = 6\) |
| d. S;\(1 \cdots 11 = 11\) | e. N;\(8 \cdots 1 = 8\) | f. H;\(12 \cdots 1 = 12\) |
20. W, W
21.
| a.\(764 \cdots (1000 - 1) = 764 \cdots 1000 - 764 \cdots 1 = 764000 - 764 = 763236\) |
| b.\(324 \cdots (100 + 2) = 324 \cdots 100 + 324 \cdots 2 = 32400 + 648 = 33048\) |
| c.\(83 \cdots (74 + 26) = 83 \cdots 100 = 8300\) |
22. Asegúrese de conocer todas las propiedades y puede proporcionar ejemplos.
23.
| a. {(3,2), (3,6), (4,2), (4,6)} |
| b. {(6,5), (7,5), (8,5), (9,5)} |
| c. {} |
| d. {(a, a)} |
| e. {(x, x), (x, y), (y, x), (y, y)} |
| f. {(1,1), (1,3), (1,5), (3,1), (3,3), (3,5), (5,1), (5,3), (5,5)} |
24. a. Se pueden utilizar dos conjuntos cualesquiera, uno con 5 elementos y otro con 2 elementos. Esta es solo una solución posible. Dejar M = {a, b, c, d, e} y dejar N = {x, y}. Dado que n (M) = 5 y n (N) = 2, entonces\(5 \times 2 = n(M \times N) = n({(a,x), (a,y), (b,x), (b,y), (c,x), (c,y), (d,x), (d,y), (e,x), (e,y)}) = 10\).
25.
| a.\(8 \times 6\) | b.\(3 \times 10\) | c.\(8 \times 6\) | d.\(5 \times 5\) | e.\(4 \times 14\) | f.\(3 \times 7\) |
28. c.\(6 \times 4\)
30.
|
a.  |
b.  |
c.  |
d.  |
e. si |
31. La propiedad distributiva de la multiplicación sobre la suma.
32. Esto se debe hacer como el ejercicio 30. Explicar los pasos así como mostrar las imágenes.
33.
| a. 8 | b. 8 | c. misma longitud |
Set de ejercicios 2 Soluciones
2.
|
\(13\ veces 29\) 1 —> 29 2 —> 58 4 —>116 8 —>232 — 232 + 116 + 29 = 377 |
\(29\ veces 13\) 1 —>13 2 —>26 4 —>52 8 —>104 16 —>208 — 208 + 104 + 52 + 13 = 377 |
3.
|
\(27\ veces 14\) 1 —> 14 2 —> 28 4 —> 56 8 —> 112 16 —> 224 — 224 + 112 + 28 + 14 = 378 |
\(14\ veces 27\) 1 —> 27 2 —>54 4 —>108 8 —>216 — 216 + 108 + 54 = 378 |
4.

5.
|
a. Respuesta: 3,591  |
b. respuesta: 29.070  |
e. Respuesta: 3,886  |
f.  |
6.
| a.\(221_{\text{four}}\) |
b.  |
| c.\(1102_{\text{four}}\) | d.\(2_{\text{four}} \times 221_{\text{four}} = 1102_{\text{four}}\) |
7.
| a.\(221_{\text{four}}\) |
b.  |
| c.\(1102_{\text{four}}\) | d.\(2_{\text{four}} \times 221_{\text{four}} = 1102_{\text{four}}\) |
8. Hacer dos pilas de base tres bloques, cada uno teniendo 2 pisos, 2 largos y una unidad. Los dos pilotes iguales se muestran a continuación.


Después, combine las pilas juntas y realice los intercambios apropiados. Después de hacer intercambios, así es como se ve:

Escribe el numeral base tres representado después de realizar todos los intercambios. La respuesta es\(1212_{\text{three}}\).
9. Hacer tres pilas de base tres bloques, cada uno teniendo 2 pisos, 2 largos y una unidad. A continuación se muestran los tres montones iguales.

Después, combine las pilas juntas y realice los intercambios apropiados. Después de hacer intercambios, así es como se ve:

Escribe el numeral base tres representado después de realizar todos los intercambios. La respuesta es\(2210_{\text{three}}\).
10.
| a. un piso | b. un piso | c. un piso | d.\(L \times L\) = F |
11.
| a. un bloque | a. un bloque | a. un bloque | d.\(F \times L\) = B |
12.
| a. un bloque largo | a. un bloque largo | a. un bloque largo | d.\(B \times L\) = LB |
13.
| a. F | b. b | c. LB | d. B | e. LB |
15.
| a. 3, 1 y 2 | b. 3 bloques, 1 plano y 2 largos |
16. Aquí solo se dan las respuestas. Asegúrate de mostrarlo con bloques y EXPLICAR.
| a.\(1032_{\text{four}}\) | b.\(10122_{\text{three}}\) |
17.
| a. un bloque largo | b. un bloque largo | c. un bloque largo | d.\(F \times F\) = LB |
18.
| a. U | b. l | c. F | d. B |
| e. L | f. F | g. B | h. F |
| i. B | j. lb |
20. La respuesta es\(20010_{\text{three}}\). Asegúrate de mostrarlo con bloques y EXPLICAR.
21. Se muestra toda la tabla:

22.
|
a.\(23_{\text{five}} \times 32_{\text{five}}\) = (2L + 3U)\(\times\) (3L + 2U) =\(2L \times 3L + 2L \times 2U + 3U \times 3L + 3U \times 2U\) = 6F + 4L + 9L + 6U = 6F + 13L + 6U = 1B + 1F + 2F + 3L + 1L + 1U = 1B + 3F + 4L + 1U =\(1341_{\text{five}}\) |
|
\(42_{text{eight}} \times 53_{\text{eight}}\) = (4L + 2U)\(\times\) (5L + 3U) =\(4L \times 5L + 4L \times 3U + 2U \times 5L + 2U \times 3U\) = 20F + 12L + 10L + 6U = 20F + 22L + 6U = 2B + 4F + 2F + 6L + 6U = 2B + 6F + 6L + 6U =\(2666_{\text{eight}}\) |
23.
\(212_{\text{four}} \times 102_{\text{four}}\)
= (2F + 1L + 2U)\(\times\) (1F + 2U)
=\(2F \times 1F + 2F \times 2U + 1L \times 1F + 1L \times 2U + 2U \times 1F + 2U \times 2U\)
= 2LB + 4F + 1B + 2L + 2F + 4U
= 2LB + 1B + 6F + 2L + 4U
= 2LB + 1B + 1B + 2F + 2L + 1 L
= 2LB + 2B + 2F + 3L
=\(22230_{\text{four}}\)
24.
|
a.\(361_{\text{nine}} \times 15_{\text{nine}}\) = (3F + 6L + 1U)\(\times\) (1L + 5U) =\(3F \times 1L + 3F \times 5U + 6L \times 1L + 6L \times 5U + 1U \times 1L + 1U \times 5U\) = 3B + 15F + 6F + 30L + 1L + 5U = 3B + 21F + 31L + 5U = 3B + 2B + 3F + 3F + 4L + 5U = 5B + 6F + 4L + 5U =\(5645_{\text{nine}}\) |
|
b.\(111_{\text{two}} \times 11_{\text{two}}\) = (1F + 1L + 1U)\(\times\) (1L + 1U) =\(1F \times 1L + 1F \times 1U + 1L \times 1L + 1L \times 1U + 1U \times 1L + 1U \times 1U\) = 1B + 1F + 1F + 1L + 1L + 1U = 1B + 2F + 2L + 1U = 1B + 1B + 1F + 1U = 1LB + 1F + 1U =\(10101_{\text{two}}\) |
25.
|
a. Respuesta:\(1422_{\text{six}}\)  |
b. Respuesta:\(1469_{\text{eleven}}\)  |
c.\(100011_{\text{two}}\) |
| d.\(T09_{\text{twelve}}\) | e.\(20211_{\text{three}}\) | f.\(2122_{\text{four}}\) |
26. Aquí sólo se muestran a, b y c. Asegúrate de hacer d y e.
 |
 |
 |
27.
| a.\(1103_{\text{five}}\) | b.\(1T58_{\text{thirteen}}\) | c.\(1022_{\text{three}}\) |
| d.\(16015_{\text{seven}}\) | e.\(16015_{\text{seven}}\) | f.\(101310_{\text{four}}\) |
29. \(2144_{\text{five}}\)
30. \(31653_{\text{seven}}\)
31. \(10001111_{\text{two}}\)
32. \(1220212_{\text{three}}\)
33. \(15417_{\text{twelve}}\)
34. \(115503_{\text{six}}\)
35. \(2012220_{\text{three}}\)
36. \(424204_{\text{six}}\)
37. \(101001010_{\text{two}}\)
38. \(T73E8_{\text{twelve}}\)
39. \(615032_{\text{eight}}\)
40. \(1033230_{\text{four}}\)
41. \(2321411_{\text{five}}\)
42. \(1563526_{\text{seven}}\)
43. \(414025_{\text{nine}}\)
44. \(8T6697_{\text{eleven}}\)
Soluciones para la tarea
1. a. 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 = 32
3. a. P;\(4 \cdots 1 = 4\)
4. a. {(3,0), (3,1), (3,6), (x,0), (x,1), (x,6)}
6.
| a. B | c. LB | e. FB |
10.
a. Propiedad asociativa de la multiplicación
Ilustrar que esta ecuación es cierta:\((2_{\text{five}} \cdots 3_{\text{five}}) \cdots 4_{\text{five}} = 2_{\text{five}} \cdots (3_{\text{five}} \cdots 4_{\text{five}}\))
Lado izquierdo:\((2_{\text{five}} \cdots 3_{\text{five}}) \cdots 4_{\text{five}} = 11_{\text{five}} \cdots 4_{\text{five}} = 44_{\text{five}}\)
Lado derecho:\(2_{\text{five}} \cdots (3_{\text{five}} \cdots 4_{\text{five}}) = 2_{\text{five}} \cdots 22_{\text{five}}) = 44_{\text{five}}\)
Ambas expresiones son iguales\(44_{\text{five}}\), entonces\((2_{\text{five}} \cdots 3_{\text{five}}) \cdots 4_{\text{five}} = 2_{\text{five}} \cdots (3_{\text{five}} \cdots 4_{\text{five}}\))
Propiedad Distributiva de Multiplicación de Adición:
Ilustrar que esta ecuación es cierta:\(2_{\text{five}} \cdots (3_{\text{five}} + 4_{\text{five}}) = (2_{\text{five}} \cdots 3_{\text{five}}) + (2_{\text{five}} \cdots 4_{\text{five)}}\)
Lado izquierdo:\(2_{\text{five}} \cdots (3_{\text{five}} + 4_{\text{five}}) = 2_{\text{five}} \cdots (12_{\text{five}}) = 24_{\text{five}}\)
Lado derecho:\((2_{\text{five}} \cdots 3_{\text{five}}) + (2_{\text{five}} \cdots 4_{\text{five}}) = 11_{\text{five}} + 13_{\trxt{five}} = 24_{\text{five}}\)
Ambas expresiones son iguales\(24_{\text{five}}\), entonces\(2_{\text{five}} \cdots (3_{\text{five}} + 4_{\text{five}}) = (2_{\text{five}} \cdots 3_{\text{five}}) + (2_{\text{five}} \cdots 4_{\text{five}}\))
Módulo 5 Operaciones Binarias
Set de ejercicios 1 Soluciones
2.
| a. 16 | b. 65 | c. 2 | d. 42 | e. 4 |
| f. 18 | g. 14 | h. 41 | i. 20 |
3.
| a. m! n = n! m; Sí; Prueba: Si m! n = n! m, entonces! es conmutativo. m! n = 2 y n! m = 2. Ya que ambas expresiones (m! n y n! m) igual a 2, entonces! es conmutativo. |
| b.\(m \bigoplus n = n \bigoplus m\); Sí; Prueba: Si\(m \bogoplus n = n \bigoplus m\), entonces\(\bigoplus\) es conmutativa. \(m \bigoplus n = 3mn\)y\(n \bigoplus m = 3nm\). Desde 3mn = 3nm, entonces\(m \bigoplus n = n \bigoplus m.\) Por lo tanto, es conmutativo. |
| c. m # n = n # m; Sí; Proporcione el suyo un ejemplo usando números. |
| d. m n = n m; Sí; Prueba: Si m n = n m, entonces es conmutativo. m n = 2m + 2n, y n m = 2n + 2m. Desde 2m + 2n = 2n + 2m, entonces m n = n m Por lo tanto, es conmutativo. |
| e.\(m \XBox n = n \XBox m\); No; Proporcione su propio contraejemplo usando números. |
| f. m, n = n, m; Sí; Prueba: Si m, n = n, m, entonces, es conmutativo. \(m , n = m^{2} + n^{2}\)y\(n , m = n^{2} + m^{2}\). Ya que\(m^{2} + n^{2} = n^{2} + m^{2}\), entonces m, n = n, m. por lo tanto,, es conmutativo. |
| g. m * n = n * m; No; Proporcione su propio contraejemplo usando números. |
| h. m |
4.
| a. 17 | b. 4 | c. 2 | d. 216 | e. 36 | f. 125 |
5.
| a. 270 | b. 34 | c. 27 | d. 6 | e. 6 |
| f. 629 | g. 6 | h. 4 | i. 12 |
6.
| a. (a! b) q c = a! (b! c); sí; Prueba: Si (a! b)! c = a! (b! c), entonces! es asociativo. (¡a! b)! c = 2! c = 2, y ¡a! (b! c) = ¡a! 2 = 2. Ya que ambos (a! b)! c y a! (b! c) son iguales a 2, entonces! es asociativo. |
| b.\((a \bigoplus b) \bigoplus c = a \bigoplus (b \bioplus c)\); sí; Prueba: Si\((a \bigoplus b)r c = a \bigoplus (b \bigoplus c)\), entonces\(\bigoplus\) es asociativo. \((a \bigoplus b) \bigoplus c = 3ab \bigoplus c = 3 \cdots 3ab \cdots c = 9abc,\)y\(a \bigoplus (b \bigoplus c) = a \bigoplus 3bc = 3 \cdots a \cdots 3bc = 9abc\). Dado que ambas expresiones\([(a \bigoplus b) \bigoplus c\) y\(a \bigoplus (b \bigoplus c)]\) son iguales a 9abc, entonces\(\bigoplus\) es asociativo. |
| c. (a # b) # c = a # (b # c); sí; Proporcione su propio ejemplo usando números. |
| d. (a b) c = a (b c); no; Proporcione su propio contraejemplo usando números. |
| e.\((a \XBox b) \XBox c = a \XBox (b \XBox c)\); no; Proporcione su propio contraejemplo usando números. |
| f. (a, b), c = a, (b, c); no; Proporcione su propio contraejemplo usando números. |
| g. (a * b) * c = a * (b * c); no; Proporcione su propio contraejemplo usando números. |
7. a @ (b + c) = (a @ b) + (a @ c)
8. a + (b @ c) = (a + b) @ (a + c)
9.
| a. a & (b $ c) = (a & b) $ (a y c) |
| b. a $ (b & c) = (a $ b) y (a $ c) |
10.
| a. a! (b r c) = (a! b) r (a! c) |
| b. no |
| c. Proporcione su propio contraejemplo usando números. |
| d.\(a \bigoplus (b ! c) = (a \bigoplus b) ! (a \bigoplus c)\) |
| e. no |
| f. proporcione su propio contraejemplo usando números. |
11.
| a.\(a + (b \cdots c) = (a + b) \cdots (a + c)\) |
| b. no |
| c. Proporcione su propio contraejemplo usando números. |
12.
| a.\(a \cdots (b \cdots c) = (a \cdots b) \cdots (a \cdots c)\) |
| b. si |
| c. Proporcione su propio ejemplo usando números. |
13.
| a. a, (b @ c) = (a, b) @ (a, c) |
| b. no |
| c. Proporcione su propio contraejemplo usando números. |
| d. a @ (b, c) = (a @ b), (a @ c) |
| e. no |
| f. proporcione su propio contraejemplo usando números. |
14. Estás por tu cuenta aquí. Sé creativo.
15.
a. m n = n n = n m; no; proporcione su propio contraejemplo usando números m; no; proporcione su propio contraejemplo usando números |
b. m n = n n = n m; sí; proporcione su propia prueba m; sí; proporcione su propia prueba |
c. (m n) n) x = m x = m (n (n x); no; proporcione su propio contraejemplo usando números x); no; proporcione su propio contraejemplo usando números |
d. (m n) n) x = m y (n x = m y (n x); no; proporcione su propio contraejemplo x); no; proporcione su propio contraejemplo |
e. a (b + c) = (a (b + c) = (a b) + (a b) + (a c); no; proporcione su propio contraejemplo c); no; proporcione su propio contraejemplo |
f. a (b + c) = (a (b + c) = (a b) + (a b) + (a c); no; proporcione su propio contraejemplo c); no; proporcione su propio contraejemplo |
g. a (b y c) = (a (b y c) = (a b) y (a b) y (a c); no; proporcione su propio contraejemplo c); no; proporcione su propio contraejemplo |
h. a (b (b c) = (a c) = (a b) b) (a (a c); no; proporcione su propio contraejemplo c); no; proporcione su propio contraejemplo |
16. \((a + b) \cdots c = (a \cdots c) + (b \cdots c)\); sí; da tu propio ejemplo
17. \((a \cdots b) + c = (a + c) \cdots (b + c)\); no; proporcione su propio contraejemplo
18. \((a + b) \div c = (a \div c) + (b \div c)\); sí; da tu propio ejemplo
19. \(a \div (b + c) = (a \div b) + (a \div c)\); no; proporcione su propio contraejemplo
20.
a. (b + c) a = (b a = (b a) + (c a) + (c a); no; proporcione su propio contraejemplo a); no; proporcione su propio contraejemplo |
b. (b + c) a = (b a = (b a) + (c a) + (c a); no; proporcione su propio contraejemplo a); no; proporcione su propio contraejemplo |
c. (b c) c) a = (b a = (b a) a) (c (c a); no; proporcione su propio contraejemplo a); no; proporcione su propio contraejemplo |
d. (b c) c) a = (b a = (b a) a) (c (c a); no; proporcione su propio contraejemplo a); no; proporcione su propio contraejemplo |
Soluciones para la tarea
1.
| a. 23 | b. 20 | c. 2a + b | d. 26 | g. 2 |
| j. 90 | m. 1 | p. 10 | s. 26 | v. 17 |
| y. 45 |
2. a. 19
3.
| a. 20 | c. 36 | e. 21 |
Módulos 6 Integrados
Set de ejercicios 1 Soluciones
1. {..., -3, -2, -1}
2. {..., -3, -2, -1, 0, 1, 2, 3,...}
3.
| a. 4 | b. 8 | c. 2 | d. 1 | e. 0 |
4.
| a. 7 | b. 13 | c. 4 | d.\(\frac{3}{7}\) | e.\(\frac{3}{7}\) | f. 6 |
5. a. 6, -6
6. a. 19, -19
7. 0
8. ninguno
9.
| a. -5 | b. +3 |
10.
|
a. -3 desde el punto terminal del último vector aterrizó en -3.  |
|
b. -9 ya que el punto terminal del último vector aterrizó en -9.  |
|
c. 4 ya que el punto terminal del último vector aterrizó en 4.  |
|
d. 1 ya que el punto terminal del último vector aterrizó en 1.  |
|
e. -2 ya que el punto terminal del último vector aterrizó en -2.  |
|
f. -60 desde el punto terminal del último vector aterrizó en -60.  |
|
g. -1 ya que el punto terminal del último vector aterrizó en -1.  |
|
h. -3 desde el punto terminal del último vector aterrizó en -3.  |
11. termómetro
12. caminar dos cuadras al este
13. Las respuestas para éstas son las mismas que para las del ejercicio 10.
14.
| a. 5 | b. -9 | c. -3 | d. 6 |
15.
| a. RRRRR | b. GG | c. RRRR |
16. 0; las razones pueden variar
17. Las respuestas variarán, pero siempre habrá el mismo número de contadores negativos que contadores positivos en cada representación.
18.
| a. -2 | b. -2 | c. -2 | d. -2 | e. -3 | f. +3 | g. +3 | h. +4 |
19. Las respuestas variarán, pero habrá 4 contadores más positivos que negativos en cada representación.
20. Las respuestas variarán, pero habrá 4 contadores negativos más que positivos en cada representación.
21.
|
a. (1) Combina 5 rojos y 3 rojos: RRRRR + RRR (2) Hay 8 rojos, RRRRRRRRRR, que representa -8. (3) Por lo tanto, -5 + -3 = -8. |
|
b. (1) Combinar 6 rojos y 9 verdes: RRRRRR + GGGGGGG = R R R R R R G G G G G G G G G G G G (2) Eliminar 6 pares rojo-verde (cero), dejando GGG, que representa -3. (3) Por lo tanto, -6 + 9 = 3. |
|
c. (1) Combinar 8 rojos y 6 verdes: RRRRRRRRRR + GGGGGG = R R R R R R R R R G G G G G (2) Eliminar 6 pares rojo-verde (cero), dejando RR, que representa -2. (3) Por lo tanto, -8 + 6 = -2. |
|
d. (1) Combinar 5 rojos, 3 rojos y 6 verdes: RRRRR + RRR + GGGGGG = R R R R R R R R G G G G G G (2) Eliminar 6 pares rojo-verde (cero), dejando RR, que representa -2. (3) Por lo tanto, -5 + -3 + 6 = -2. |
|
e. (1) Combinar 6 rojos, 9 verdes y 1 rojo: RRRRRRR + GGGGGGG + R = R R R R R R R G G G G G G G G G G G G G G G G G (2) Eliminar 7 pares rojo-verde (cero), dejando GG que representa +2. (3) Por lo tanto, -6 + 9 + -1 = +2. |
|
f. (1) Combina 4 greens, 6 verdes y 5 rojos: GGGG + GGGGGG + RRRRR = G G G G G G G G G G R R R R R R R (2) Eliminar 5 pares rojo-verde (cero), dejando GGGGG, que representa +5. (3) Por lo tanto, +4 + +6 + -5 = +5. |
22.
|
a. (1) 6 — 3 significa eliminar 3 greens de una colección de contadores que representan 6. (2) Representa 6 con 6 greens: GGGGGG (3) Retire 3 greens, dejando GGG, que representa +3. (4) Por lo tanto, 6 — 3 = 3 |
|
b. (1) 4 — 6 significa eliminar 6 greens de una colección de contadores que representan 4. (2) Representa 4 con 4 greens: GGGG (3) Añadir 2 pares rojo-verde (cero) a la colección: G G G G G R R (4) Eliminar 6 greens, dejando RR, que representa -2. (5) Por lo tanto, 4 — 6 = -2 |
|
c. (1) -7 — -6 significa eliminar 6 rojos de una colección de contadores que representan -7. (2) Representa -7 con 7 rojos: RRRRRRRR (3) Eliminar 6 rojos, dejando R, que representa -1. (4) Por lo tanto, -7 — (-6) = -1 |
|
d. (1) -3 — -7 significa eliminar 7 rojos de una colección de contadores que representan -3. (2) Representa -3 con 3 rojos: RRR (3) Añadir 4 pares rojo-verde (cero) a la colección: R R R R R R R G G G (4) Eliminar 7 rojos, dejando GGGG, que representa +4. (5) Por lo tanto, -3 — (-7) = +4 |
|
e. (1) 4 — -3 significa eliminar 3 rojos de una colección de contadores que representan +4. (2) Representar +4 con 4 greens: GGGG (3) Añadir 3 pares rojo-verde (cero) a la colección: G G G G G G R R R (4) Eliminar 3 rojos, dejando GGGGG, que representa +7. (5) Por lo tanto, 4 — (-3) = +7 |
|
f. (1) -2 — 5 significa eliminar 5 greens de una colección de contadores que representan -2. (2) Representar -2 con 2 rojos: RR (3) Añadir 5 pares rojo-verde (cero) a la colección: R R R R R R R G G G G (4) Retire 5 greens, dejando RRRRRRRR, que representa -7. (5) Por lo tanto, -2 — 5 = -7 |
|
g. (1) 5 — 5 significa eliminar 5 greens de una colección de contadores que representan 5. (2) Representa 5 con 5 greens: GGGGG (3) Quitar 5 greens, sin dejar nada, lo que representa 0. (5) Por lo tanto, ,5 — 5 = 0 |
|
h. (1) 5 — (-5) significa eliminar 5 rojos de una colección de contadores que representan 5. (2) Representa 5 con 5 greens: GGGGG (3) Añadir 5 pares rojo-verde (cero) a la colección: G G G G G G G G G G G G R R R R (4) Eliminar 5 rojos, dejando GGGGGGGG, que representa 10. (5) Por lo tanto, 5 — (-5) = +10 |
|
i. (1) -4 — (- 4) significa eliminar 4 rojos de una colección de contadores que representan -4. (2) Representa -4 con 4 rojos: RRRR (3) Quitar 4 rojos, sin dejar nada, lo que representa 0.. (5) Por lo tanto, -4 — -4 = 0. |
|
j. (1) -6 — 6 significa eliminar 6 greens de una colección de contadores que representan -6. (2) Representa -6 con 6 rojos: RRRRRR (3) Añadir 6 pares rojo-verde (cero) a la colección: R R R R R R R R R R R G G G G G G (4) Quitar 6 greens, dejando RRRRRRRRRRRRRR, que representa -12. (5) Por lo tanto, -6 — 6 = -12 |
23.
|
a. (1) 5 — 8 significa eliminar 8 greens de una colección de contadores que representan 5. (2) Representa 5 con 5 greens: GGGGG (3) Añadir 3 pares rojo-verde (cero) a la colección: G G G G G G G R R R (4) Eliminar 8 greens, dejando RRR, que representa -3. (5) Por lo tanto, 5 — 8 = -3 |
|
b. (1) 5 + -8 medias combinan 5 verdes y 8 rojos: GGGGG + RRRRRRR = G G G G G R R R R R R R R R R R (2) Eliminar 5 pares rojo-verde (cero), dejando RRR, que representa -3. (3) Por lo tanto, 5 + -8 = -3. |
| c. Las respuestas son las mismas. |
24. Hay varias formas de hacer este problema. Pero en todo caso, el cobro final para cada uno debe dar la misma respuesta.
25.
|
a. 1ª vía: Eliminar 3 greens de una colección que represente -5. 2da forma: Combina una colección de 5 rojos y 3 rojos juntos. |
|
b. 1ª vía: Eliminar 8 greens de una colección que represente +4. 2da forma: Combina una colección de 4 greens y 8 rojos juntos. |
|
c. 1a vía: Eliminar 7 rojos de una colección que representa -9. 2da forma: Combina una colección de 9 rojos y 7 verdes juntos. |
|
d. 1ª vía: Eliminar 10 rojos de una colección que represente -10. 2da forma: Combina una colección de 10 rojos y 10 verdes juntos. |
26.
| a. 4 + (-5) | b. -9 + (-7) | c. -3 + (+4) |
27.
| a. 4 + -5 + -7 + -6 + +9 | b. -43 + (+75) + 12 + 63 + (-9) |
28.
| a. -6 | b. +8 | c. negativo, negativo | d. positivo, positivo | e. opuesto |
29.
| a. Cuando el minuendo y el sustraendo son el mismo número | b. 0 |
30.
|
a. 10 — 4 = +6  |
e. 3 — 10 = -7  |
|
b. -7 — 5 = -12  |
f. -5 — (-8) = +3  |
|
c. 8 — (-3) = +11  |
g. 6 — (-6) = +12  |
|
d. -9 — -1 = -8  |
h. 9 — 9 = 0  |
31.
| a. 1 — (-5) = +6 | b. 13 — 10 = +3 | c. 3 — 8 = -5 |
32.
| a. -92 — -71 = -21 | d. -122 — 76 = -198 |
| b. 92 — -81 = +173 | e. 208 — 389 = -181 |
| c. -110 — -200 = +90 | a. 46 + -76 + 92 = 138 + -76 = 62 |
33.
| a. 46 + -76 + 92 = -30 + 92 = 62 |
| b. -63 + 94 + 45 + -71 = 31 + 45 + -71 = 76 + -71 = 5 |
34.
| a. 46 + -76 + 92 = 138 + -76 = 62 |
| b. -63 + 94 + 45 + -71 = 139 + -134 = 5 |
35.
| a. Cerrado |
| a. Cerrado |
| a. Cerrado |
| d. No Cerrado; un contraejemplo es: 7 — 10 = -3 |
| e. Cerrado |
| f. No Cerrado; un contraejemplo es: -11 — -20 = +9 |
| g. No cerrado; un contraejemplo es: 1 + 1 = 2 |
| h. No cerrado; un contraejemplo es: 1 — -1 = 2 |
Set de ejercicios 2 Soluciones
1.
| a. R R R R R G |
| b. R R R R R R R R R R R R R R R R G G G |
| c. RRRRRRRRRRRRR = -12 |
2.
| a. R R R R R R G G |
| b. R R R R R R R R R R R R R R R R R R R G G G G G G G G G |
| c. RRRRRRRRRRRRR = -12 |
3.
| a. R R R R |
| b. r r r r r r r r r r r r r |
| c. -12 |
4.
| a.\(4 \times -2\) significa combinar 4 juegos de 2 rojos: RR + RR + RR + RR = RRRRRRRR = -8 |
| b.\(3 \times 5\) significa combinar 3 juegos de 5 greens: GGGGG + GGGGG + GGGGG = GGGGGGGGGGGGG = +15 |
| c.\(5 \times -3\) significa combinar 5 juegos de 3 rojos: RRR + RRR + RRR + RRR + RRR + RRR = RRRRRRRRRRRRRRR = -15 |
| d.\(7 \times 2\) significa combinar 7 juegos de 2 greens: GG + GG + GG + GG + GG + GG + GG + GG = GGGGGGGGGGGG = +14 |
| e.\(0 \times -3\) medias para combinar 0 conjuntos de 3 rojos = 0 |
5.
| a. R R R R R R R R R R R R R R R G G G G G G G G G G G G G G G G |
| b. R R R R R R R R R R R R R R R R G G |
| c. R R R R R R R R R R R R R = -12 |
6.
| a. R R R R R R R R R R R R R G G G G G G G G G G G G G G G |
| b. r r r r r r r r r r r r r |
| c. -12 |
7.
|
a.\(-5 \times 3\) significa eliminar 5 juegos de 3 greens de una colección que representa cero. (1) Que el cero esté representado por 15 rojos y 15 verdes: R R R R R R R R R R R R R R R R R R R R R R G G G G G G G G G G G G G (2) Retire 5 juegos de 3 greens de la colección anterior, que deja RRRRRRRRRRRRRRRRRR, que representa -15. Por lo tanto,\(-5 \times 3 = -15\). |
|
b.\(-3 \times 2\) significa eliminar 3 juegos de 2 greens de una colección que representa cero. (1) Dejar que el cero esté representado por 6 rojos y 6 verdes: R R R R R R R R G G G G G (2) Retire 3 juegos de 2 greens de la colección anterior, que deja RRRRRR, que representa -6. Por lo tanto,\(-3 \times 2 = -6\) |
| c.\(2 \times -3\) significa combinar 2 juegos de 3 rojos: RRR + RRR = RRRRR = -6. Por lo tanto\(2 \times -3 = -6\) |
|
d.\(-2 \times 3\) significa eliminar 2 juegos de 3 greens de una colección que representa cero. (1) Que el cero esté representado por 6 rojos y 15 verdes: R R R R R R R R G G G G G (2) Eliminar 2 juegos de 3 verdes de la colección anterior, que deja RRRRRR, que representa -6. Por lo tanto,\(-2 \times 3 = -6\). |
| e.\(3 \times 2\) medias para combinar 3 juegos de 2 greens: GG + GG + GG = GGGGGG = 6. Por lo tanto\(3 \times 2 = 6\) |
| f.\(0 \times -4\) significa combinar 0 conjuntos de 4 rojos = 0 |
|
g.\(-4 \times 0\) significa eliminar 4 conjuntos de 0 contadores de una colección que representa cero. (1) Elija cualquier representación de cero. Una posibilidad es dejar que el cero esté representado por 6 rojos y 6 verdes. R R R R R R R R G G G G G (2) Eliminar 0 conjuntos de 0 contadores de la colección anterior, que deja la colección original, que representa 0. Por lo tanto,\(-4 \times 0 = 0\). |
8.
\(-3 \times 6\): Eliminar 3 juegos de 6 greens de cero; 5G y 23R; -18
\(-3 \times 6\): Eliminar 3 juegos de 6 greens de cero; 18R; -18
\(-4 \times 4\): Eliminar 4 juegos de 4 greens de cero; 2G y 18R; -16
\(-4 \times -4\): Eliminar 4 juegos de 4 rojos de cero; 18G y 2R; 16
\(-5 \times 2\): Eliminar 5 juegos de 2 greens de cero; 4G y 14R; -10
\(-2 \times 5\): Eliminar 2 juegos de 5 greens de cero; 3G y 13R; -10
\(-5 \times -2\): Eliminar 5 juegos de 2 rojos de cero; 11G y 1R; 10
\(-2 \times -5\): Eliminar 2 juegos de 5 rojos de cero; las respuestas variarán; 10
\(-3 \times 3\): Eliminar 3 juegos de 3 greens de cero; 1G y 10R; -9
\(-3 \times -3\): Eliminar 3 juegos de 3 rojos de cero; 12G y 3R; 9
\(-7 \times 2\): Eliminar 7 juegos de 2 greens de cero; las respuestas variarán; -14
\(-2 \times 8\): Eliminar 2 juegos de 8 greens de cero; 2G y 18R; -16
\(-2 \times -8\): Eliminar 2 juegos de 8 rojos de cero; 18G y 2R; 16
9.
| a. positivo | b. negativo | c. cero | d. positivo |
10.
| a. Cerrado |
| b. cerrado |
| c. No Cerrado: un contraejemplo es:\(-2 \times -8 = 16\) |
| d. No cerrado: un contraejemplo es:\(-1 \times -1 = 1\) |
| e. Cerrado |
| f. cerrado |
11.
| a. verdadero |
| b. verdadero |
| c. verdadero |
| d. false; 2 < 3; Multiplicar ambos lados por 5:\(2 \times 5 > 3 \times 5\) es falso. |
| e. verdadero |
| f. false: 2 < 3; Multiplicar ambos lados por -5:\(2 \times -5 > 3 \times -5\) es falso. |
12.
| a. Si a > b y b > c, entonces a > c |
| b. Si a > b, entonces a + c > b + c |
| c. Si a > b, entonces ap > bp |
| d. Si a > b, entonces un < bn |
Soluciones para la tarea
2.
| a. 16 | c. 2 | e. 8 |
3. a. 4 y -4
4.
| a. +7 | c. -9 |
5.
| a. 2 — (-5) | c. 3 — 12 |
6. -8 + 5 + (-3) = -6, ya que el punto terminal del último vector aterrizó en -6.

8.
|
a. 5 — 11 = -6  |
|
c. 5 — (-11) = 16  |
9.
a. (1) -4 + (-3) significa combinar 4 rojos y 3 rojos: RRRR + RRR = RRRRRRR, que representa -7
(2) Por lo tanto, -4 + -3 = -7
10.
a. (1) 6 — 8 significa eliminar 8 greens de una colección de contadores que representan +6.
(2) Representar +6 con 6 greens: GGGGGG
(3) Añadir 2 pares rojo-verde (cero) a la colección:
G G G G G G G
R R
(4) Eliminar 8 greens, dejando RR, que representa -2.
(5) Por lo tanto, 6 — 8 = -2
11.
| a. Cerrado |
| b. No cerrado; un contraejemplo es 3 — 10 = -7 |
| c. Cerrado |
12.
a.\(-5 \times 3\) significa eliminar 5 juegos de 3 greens de una colección que representa cero.
(1) Que el cero esté representado por 15 rojos y 15 verdes:
R R R R R R R R R R R R R R R R R R R R R R
G G G G G G G G G G G G G
(2) Retire 5 juegos de 3 greens de la colección anterior, que deja
RRRRRRRRRRRRRRRRRR, que representa -15. Por lo tanto,\(-5 \times 3 = -15\).
Soluciones para la tarea
2.
| a. 16 | c. 2 | e. 8 |
3. a. 4 y -4
4. a +7
5.
| a. 2 — (-5) | c. 3 — 12 |
6. -8 + 5 + -3 = -6, ya que el punto terminal del último vector aterrizó en -6.

8.
|
a. 5 — 11 = -6  |
|
c. 5 — (-11) = 16  |
9.
a. (1) -4 + -3 significa combinar 4 rojos y 3 rojos: RRRR + RRR = RRRRRRR, que representa -7
(2) Por lo tanto, -4 + -3 = -7
10.
a. (1) 6 — 8 significa eliminar 8 greens de una colección de contadores que representan +6.
(2) Representar +6 con 6 greens: GGGGGG
(3) Añadir 2 pares rojo-verde (cero) a la colección:
G G G G G G G
R R
(4) Eliminar 8 greens, dejando RR, que representa -2.
(5) Por lo tanto, 6 — 8 = -2
11.
| a. Cerrado |
| b. No cerrado; un contraejemplo es 3 — 10 = -7 |
| c. Cerrado |
12.
a.\(-5 \times 3\) significa eliminar 5 juegos de 3 greens de una colección que representa cero.
(1) Que el cero esté representado por 15 rojos y 15 verdes:
R R R R R R R R R R R R R R R R R R R R R R
G G G G G G G G G G G G G
(2) Eliminar 5 juegos de 3 verdes de la colección anterior, que deja RRRRRRRRRRRRRRRRRR, que representa -15. Por lo tanto,\(-5 \times 3 = -15\).
Módulo 7 División
Set de ejercicios 1 Soluciones
1.
| a. 2 | b. R | c. R, R |
2.
|
a. P, W, P, W 9, 2, 4, 1, 9, 4, 2, 1  |
|
b. l, r, l, r, 11, 3, 3, 2, 11, 3, 3, 2  |
|
c. R, blanco (o 0), R, blanco (o 0), 8, 4, 2, blanco (o 0), 8, 2, 4, blanco (o 0)  |
|
d. W, L, W, L, 7, 4, 1, 3, 7, 1, 4, 3  |
|
e. R, blanco (o 0), R, blanco (o 0), 6, 3, 2, blanco (o 0), 6, 2, 3, blanco (o 0)  |
3. 2 pilas iguales de 18 unidades cada una

4.
| a.\(210_{\text{four}\) |
| b. Los métodos variarán. |
| c.\(102_{\text{four}}\) |
| d.\(210_{\text{four}}, 102_{\text{four}}\) |
5.
| a.\(1100_{\text{three}}\) |
| b. Los métodos variarán. |
| c.\(200_{\text{three}}\) |
| d.\(1100_{\text{three}}, 200_{\text{three}}\) |
7.
| a.\(210_{\text{four}}\) |
| b. Los métodos variarán. |
| c.\(30_{\text{four}}\) |
| d.\(210_{\text{four}}, 30_{\text{four}}\) |
9.
| a.\(100 \div 4\) |
| b. Partición en subconjuntos |
| c. Desembolsar 100 canicas en 4 subconjuntos iguales. |
|
d.  |
| e.\(4 \cdots 25\) |
| f. Contar cuántas canicas se colocaron en uno de los subconjuntos iguales. |
| g. 25 |
10.
| a.\(80 \div 8\) |
| b. Sustracción repetida |
| c. Poner 8 onzas en un subconjunto a la vez. |
|
d.  |
| e.\(10 \cdots 8\) |
| f. Contar cuántos subconjuntos, cada uno con 8 onzas, se hicieron. |
| g. 10 |
11.
| a.\(144 \div 16\) |
| b. Sustracción repetida |
| c. Cuenta 16 páginas a la vez. |
|
d.  |
| e.\(9 \cdots 16\) |
| f. contar cuántos cuentos, cada uno con 16 páginas, se hicieron. |
| g. 9 |
12.
| a.\(500 \div 4\) |
| b. Partición en subconjuntos |
| c. Desembolsar $500 en 4 subconjuntos iguales. |
|
d.  |
| e.\(4 \cdots 125\) |
| f. contar cuánto dinero se colocó en uno de los subconjuntos iguales. |
| g. $125 |
13.
| a.\(8 \div 1\frac{1}{3}\) |
| b. Sustracción repetida |
| c. Poner 1\(\frac{1}{3}\) tazas en un subconjunto a la vez. |
|
d.  |
| e.\(6 \cdots 1\frac{1}{3}\) |
| f. Contar cuántos subconjuntos se formaron. |
| g. 6 |
14.
| a.\(65 \div 13\) |
| b. Partición en subconjuntos |
| c. Desembolsa 65 pelones de beisboles en 13 subconjuntos iguales. |
|
d.  |
| e.\(13 \cdots 5\) |
| f. Contar cómo se colocaron las pelotas de beisbolín en uno de los subconjuntos iguales. |
| g. 5 |
15.
|
d.  |
| e.\(12 \cdots 4\) |
|
g.  |
| h.\(4 \cdots 12\) |
16.
|
d.  |
| e.\(4 \cdots 50\) |
| g. Poner 4 en un subconjunto a la vez. |
| h.\(50 \cdots 4\) |
17.
| d. Dibuja 50 subconjuntos y luego desembolsa 150 entre los 50 subconjuntos. |
| e.\(50 \cdots 3\) |
|
g.  |
| h.\(3 \cdots 50\) |
18.
| d. Dibuja 35 subconjuntos y luego desembolsa 140 entre los 35 subconjuntos. |
| e.\(35 \cdots 4\) |
|
g.  |
| h.\(4 \cdots 35\) |
19.
|
d.  |
| e.\(5 \cdots 19\) |
| g. Poner 5 en un subconjunto a la vez. |
| h.\(19 \cdots 5\) |
19.
|
d.  |
| e.\(5 \cdots 19\) |
| g. Poner 5 en un subconjunto a la vez. |
| h.\(19 \cdots 5\) |
19.
|
d.  |
| e.\(5 \cdots 19\) |
| g. Poner 5 en un subconjunto a la vez. |
| h.\(19 \cdots 5\) |
22.
| a.\(56 \div 8\) |
| b.\(40 \div 5\) |
23.
| a.\(18 \div 9\) |
| b.\(10 \div 2\) |
24. a representa cuántos subconjuntos y b representa cuántos hay en cada subconjunto.
25.
| a. Desde 32 = 8\(\cdots\) 4, entonces\(32 \div 8\) = 4 |
| b. Desde 56 = 8\(\cdots\) 7, luego 56\(\div\) 8 = 7 |
| c. Desde 32 = 2\(\cdots\) 16, luego 32\(\div\) 2 = 16 |
| d. Desde 0 = 13\(\cdots\) 0, luego 0\(\div\) 13 = 0 |
| e. Desde 12 = 1\(\cdots\) 12, luego 12\(\div\) 1 = 12 |
| f. Dado que X = 1\(\cdots\) X, entonces X\(\div\) 1 = X |
| g. Desde 0 = Y\(\cdots\) 0, entonces 0\(\div\) Y = 0 |
26.
| c. Desde 48 = 6\(\cdots\) 8, luego 48\(\div\) 6 = 8 |
| d. Como no existe una solución de números enteros para hacer verdadera la ecuación 35= 4\(\cdots\) __, 35\(\div\) 4 no se define bajo números enteros. |
| e. Desde 48 = 1\(\cdots\) 48, luego 48\(\div\) 1 = 48 |
| f. Como no existe una solución de números enteros para hacer verdadera la ecuación 55 = 7\(\cdots\) __, 55\(\div\) 7 no se define bajo números enteros. |
| g. Desde 0 = 8\(\cdots\) 0, luego 0\(\div\) 8 = 0 |
| e. 203 r. 314 |
| f. 248 r. 14 |
27.
| a. no hay ningún número que haga la ecuación, 6 = 0\(\cdots\) ____ verdadera, ya que cualquier número puesto en el blanco hará que el lado derecho de la ecuación sea cero, lo que nunca puede igualar al lado izquierdo de la ecuación, que es 6. Por lo tanto, no\(6 \div 0\) se define. |
| b. no hay ningún número que haga la ecuación, 18 = 0\(\cdots\) ____ verdadera, ya que cualquier número puesto en el blanco hará que el lado derecho de la ecuación sea cero, lo que nunca puede igualar al lado izquierdo de la ecuación, que es 18. Por lo tanto, no\(18 \div 0\) se define. |
| c. No hay un número que haga verdadera la ecuación, M = 0\(\cdots\) ____, ya que cualquier número que se ponga en blanco hará que el lado derecho de la ecuación sea cero, lo que nunca puede igualar al lado izquierdo de la ecuación, que es M (ya que se supone que M no es igual a cero). Por lo tanto, no\(M \div 0\) se define. |
Set de ejercicios 2 Soluciones
1.
| a. 6 r. 43 |
| b. 7 r. 20 |
| c. 8 r. 8 |
| d. 3 r. 194 |
| e. 5 r. 55 |
| f. 5 r. 165 |
| g. 9 r. 239 |
2.
| a. 45 r. 15 |
| b. 12 r. 27 |
| c. 32 r. 34 |
| d. 81 r. 29 |
3.
| a. 45 r. 15 |
| b. 12 r. 27 |
| c. 32 r. 34 |
| d. 81 r. 29 |
| e. 203 r. 314 |
| f. 248 r. 14 |
Set de ejercicios 3 Soluciones
1.
| a. F F L L U U |
|
b. i. LUU, LUU, LUU, LUU, LUU ii. U |
| c. UUUU |
| d. cociente: LUU, resto: U |
| e.\(12_{\text{three}}r. 1_{\text{three}}\) |
| f.\(12_{\text{three}} \cdots 12_{\text{three}} + 1_{\text{three}} = 221_{\text{three}} + 1_{\text{three}} = 222_{\text{three}}\) |
2.
| a.\(13_{\text{five}}r. 3_{\text{five}}\) |
| b.\(32_{\text{six}}r. 21_{\text{six}}\) |
| c.\(11_{\text{four}}r. 10_{\text{four}}\) |
| d.\(110_{\text{two}}r. 1_{\text{two}}\) |
3.
| a.\(23_{\text{seven}}r. 3_{\text{seven}}\) |
| b.\(102_{\text{three}}\) |
Set de ejercicios 3 Soluciones
1.
| a. F F L L U U |
|
b. i. LUU, LUU, LUU, LUU, LUU ii. U |
| c. UUUU |
| d. cociente: LUU, resto: U |
| e.\(12_{\text{three}}r. 1_{\text{three}}\) |
| f.\(12_{\text{three}} \cdots 12_{\text{three}} + 1_{\text{three}} = 221_{\text{three}} + 1_{\text{three }}= 222_{\text{three}}\) |
2.
| a.\(13_{\text{five}}r. 3_{\text{five}}\) |
| b.\(32_{\text{six}}r. 21_{\text{six}}\) |
| c.\(11_{\text{four}} r. 10_{\text{four}}\) |
| d.\(110_{\text{two}} r. 1_{\text{two}}\) |
3.
| a.\(23_{\text{seven}}r. 3_{\text{seven}}\) |
| b.\(102_{\text{three}}\) |
4. \(12_{\text{three}}r. 1_{\text{three}}\)
5. \(13_{\text{five}}r. 3_{\text{five}}\)
6. \(11_{\text{four}}r. 10_{\text{four}}\)
7. \(32_{\text{six}}r. 21_{\text{six}}\)
8. \(110_{\text{two}}r. 1_{\text{two}}\)
9. \(23_{\text{seven}}r. 3_{\text{seven}}\)
10. \(102_{\text{three}}\)
11. \(31_{\text{five}}r. 2_{\text{five}}\)
12. \(111_{\text{two}}r. 101_{\text{two}}\)
13. \(61_{\text{eight}}r. 6_{\text{eight}}\)
14. \(T2_{\text{thirteen }}r. E_{\text{thirteen}}\)
15. \(23_{\text{twelve}}r. 1E_{\text{twelve}}\)
Soluciones para la tarea
1.
| a.\(72 \div 4\) |
| b. Sustracción repetida |
| c. Pon 4 piruletas en una bolsa a la vez restando repetidamente 4 de 72 hasta que te quedes sin piruletas. |
|
d.  |
| e.\(18 \cdots 4\) |
| f. cuenta cuántos subconjuntos de 4 hiciste, cuántas bolsas de piruletas hay. |
| g. 18 |
7.
|
a.  |
|
b.  |
| c. Particionar en subconjuntos es más fácil, ya que solo necesitas hacer 2 subconjuntos iguales en lugar de restar 2 a la vez. |
11.
| a. el número de subconjuntos |
| b. cantidad en cada subconjunto |
13. \(56_{\text{seven}}r. 22_{\text{seven}}\)
15. \(285_{\text{eleven}}r. 167_{\text{eleven}}\)
17. \(2111_{\text{three}}r. 210_{\text{three}}\)
18.
| a. No cerrado;\(-1 \div -1 = 1\) |
| c. No cerrado; no\(1 \div 0\) está definido |
19. No;\(10 \div 2 = 5\), pero\(2 \div 10 = 1/2\). Por lo tanto,\(10 \div 2 \nleq 2 \div 10\). Usa un contraejemplo diferente en tus respuestas.
Módulo 8 Teoría de Números
Set de ejercicios 1 Soluciones
1.
| a. 7 | b. 3 |
| c. 8 | d. 1 |
| e. 2 | f. 8 |
| g. 2 | h. 8 |
| i. 0 | j. 2 |
| k. 4 | l. 0 |
| m. 7 | n. 8 |
2. mismas respuestas que para el ejercicio 1
3. Sí.
4.
|
a. Ck: 6 + 7 = 13 → 4 \(4 \nleq 2\); error |
|
b. Ck: 5 + 1 = 6 6 = 6; correcto |
|
c. Ck: 2 + 3 = 5 \(5 \nleq 4\); error |
|
d. Ck: 8 + 2 + 5 = 15 → 6 6 = 6; correcto |
|
e. Ck: 5 + 2 + 2 = 9 → 0 \(0 \nleq 3\); error |
|
f. Ck: 1 + 7 + 0 = 8 8 = 8; correcto |
5.
|
a.\(2 \cdots 8 = 16 → 7\) 7 = 7; correcto |
|
b.\(2 \cdots 0 = 0\) \(0 \nleq 8\); error |
|
c.\(5 \cdots 1 = 5\) 5 = 5; correcto |
|
d.\(2 ·\cdots 7 = 14 → 5\) \(5 \nleq 4\); error |
|
e.\(0 \cdots 1 = 0\) 0 = 0; correcto |
|
f. 3 · 7 = 21 → 3 \(3 \nleq 4\); error |
|
g.\(2 \cdots 7 = 14 → 5\) 5 = 5; correcto |
|
h.\(5 \cdots 2 = 10 → 1\) \(1 \nleq 0\); error |
|
i.\(2 \cdots 6 = 12 → 3\) 3 = 3; correcto |
6. Haz los problemas, luego revisa tus respuestas usando raíces digitales.
7.
|
a. 0 + 5 = 5 5 = 5; correcto |
|
b. 8 + 0 = 8 8 = 8; correcto |
|
c. 5 + 3 = 8 \(8 \nleq 6\); error |
|
d. 8 + 6 = 14 → 5 \(5 \nleq 4\); error |
|
e. 5 + 4 = 9 → 0 0 = 0; correcto |
|
f. 1 + 4 = 5 5 = 5; correcto |
8. Haz los problemas, luego revisa tus respuestas usando raíces digitales.
9.
|
a.\(1 \cdots 4 = 4; 4 + 7 = 11 → 2\) 2 = 2; correcto |
|
b.\(6 \cdots 0 = 0; 0 + 0 = 0\) 0 = 0; correcto |
|
c.\(8 \cdots 8 = 64 → 10 → 1; 1 + 1 = 2\) \(2 \nleq 4\); error |
|
d.\(6 \cdots 3 = 18 → 0; 0 + 5 = 5\) 5 = 5; correcto |
10. Haz el problema, luego revisa tu respuesta usando raíces digitales.
11.
| a. Este es un problema de división. La respuesta es 5. |
| b. Se trata de una declaración falsa ya que 35 no es un factor de 7. |
| c. Esta es una afirmación verdadera ya que 7 es un factor de 35; (\(7 \cdots 5 = 35\)) |
| d. Se trata de un problema de división. La respuesta es 5 r. 5. |
| e. Se trata de una declaración falsa ya que 56 no es un factor de 8. |
| f. se trata de una declaración falsa ya que 7 no es un factor de 40. |
| g. Esta es una afirmación verdadera ya que 12 es un factor de 60; (\(12 \cdots 5 = 60\)) |
| h. Este es un problema de división. La respuesta es 2 r. 20. |
| i. Este es un problema de división. La respuesta es 14. |
| j. Esta es una declaración falsa ya que 42 no es un factor de 3. |
| k. Esta es una afirmación verdadera ya que 6 es un factor de 42; (\(6 \cdots 7 = 42\)) |
| l. Este es un problema de división. La respuesta es 8. |
| m. Este es un problema de división. La respuesta es 50. |
| n. Esta es una afirmación verdadera ya que 4 es un factor de 100; (\(4 \cdots 25 = 100\)) |
| o. se trata de una declaración falsa ya que 4 no es un factor de 90. |
| p. Esta es una declaración falsa ya que 25 no es un factor de 5. |
13. El comprobante se escribe exactamente igual que el Ejemplo 1 mostrado arriba de este ejercicio si a se sustituye por x, b se sustituye por y, y c se sustituye por z.
18. Si a es un factor de b, entonces am = b para algún número entero, m. Si a es un factor de c, entonces a = c para algún número entero n. Usando la sustitución, bc = (am) (a) = a (amn), que muestra a es un factor de bc.
19. El comprobante se escribe exactamente igual que el ejemplo mostrado arriba de este ejercicio si a se sustituye por c, b se sustituye por a, y c se sustituye por b.
20.
| a. 2|9,712 ya que el último dígito es par. |
| b. 5.643 es impar, por lo que no es divisible por 2. |
| c. 5.690 no es divisible por 4 ya que 4 no es un factor de 90. |
| d. 63,868 es divisible por 4 ya que 4 es un factor de 68. |
| e. 854.100 es divisible por 4 ya que 4 es un factor de 0. |
| f. 8 es un factor de 12,345,248 ya que 8 es un factor de 248. |
| g. 54.094.422 no es divisible por 8 ya que 8 no es un factor de 422. |
21.
| a. 5|9,750 ya que el último es 0. |
| b. 5|5,645 ya que el último es 5. |
| c. 5.696 no es divisible por 5 ya que el último dígito no es 0 o 5. |
| d. 10|63,860 ya que el último dígito es 0. |
| e. 854.105 no es divisible por 10 ya que el último dígito no es 0. |
22.
| a. 3|9,750 desde 3|3, donde 3 es la raíz digital de 9,750. |
| b. 3|5,645 es falso ya que 3 no es un factor de 2, que es el d.r. de 5,645. |
| c. 3|5,696 es falso ya que 3 no es un factor de 8, el d.r. de 5,696. |
| d. 3|63,860 es falso ya que 3 no es un factor de 5, el d.r. de 63,860. |
| e. 3|854.115 desde 3|6, donde 6 es el d.r. de 854.115. |
23.
| a. 9|9,753 es falso ya que la raíz digital de 9,753 es 6, no 0. |
| b. 9|5,646 es falso ya que el d.r. de 5,646 es 3, no 0. |
| c. 9|5,697 ya que la raíz digital de 5,697 es 0. |
| d. 9|63,576 ya que la raíz digital de 63,576 es 0. |
| e. 9|854,103 es falso ya que el d.r. de 854,103 es 3, no 0. |
24.
| a. 6|9.753 es falso ya que 9.753 no es par, por lo tanto no es divisible por 2. |
| b. 6|5,645 es falso ya que 5,645 no es par, por lo tanto no es divisible por 2. |
| c. 6|5,696 es falso ya que 3 no es un factor de 8, que es el d.r. de 5,696. |
| d. 6|63,876 ya que es par y también es divisible por 3, ya que el d.r. es 3. |
| e. 6|854,103 es falso ya que 854,103 no es par, por lo tanto no es divisible por 2. |
25.
| a. 15|9.753 es falso ya que no es divisible por 5. |
| b. 15|6,645 ya que tanto 3 como 5 son factores. |
| c. 15|1,690 es falso ya que 3 no es un factor. |
| d. 15|63,872 es falso ya que 5 no es un factor. |
| e. 15|654,105 ya que es divisible tanto por 3 como por 5. |
26. Incluir justificación
| a. verdadero |
| b. falso |
| c. verdadero |
| d. verdadero |
27. Incluir justificación
| a. verdadero |
| b. falso |
| c. falso |
| d. verdadero |
| e. falso |
Set de ejercicios 2 Soluciones
1. c. 1, 2, 3, 4, 6, 12
2.
| a. 1, 2 |
| b. 1, 3 |
| c. 1, 2, 4 |
| d. 1, 5 |
| e. 1, 2, 3, 6 |
| g. 1, 2, 4, 8 |
| h. 1, 3, 9 |
| i. 1, 2, 5, 10 |
| j. 1, 11 |
| k. 1, 13 |
| l. 1, 2, 7, 14 |
| m. 1, 3, 5, 15 |
| n. 1, 2, 4, 8, 16 |
3.
| a. 2, 3, 5, 7, 11, 13 |
| b. Los únicos factores son 1 y el número en sí. |
| c. 4, 9, 16 |
| d. Son cuadrados perfectos. |
4.
| a.\(45 = 3 \cdots 3 \cdots 5\) |
| b.\(65 = 5 \cdots 13\) |
| c.\(200 = 2 \cdots 2 \cdots 2 \cdots 5 \cdots 5\) |
| d.\(91 = 7 \cdots 13\) |
| e.\(76 = 2 \cdots 2 \cdots 19\) |
| f.\(350 = 2 \cdots 5 \cdots 5 \cdots 7\) |
| g.\(189 = 3 \cdots 3 \cdots 3 \cdots 7\) |
| h.\(74 = 2 \cdots 37\) |
| i.\(512 = 2 \cdots 2 \cdots 2 \cdots 2 \cdots 2 \cdots 2 \cdots 2 \cdots 2 \cdots 2\) |
| j.\(147 = 3 \cdots 7 \cdots 7\) |
5. 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97
6. 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48
7. 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, 100, 102, 104, 105, 106, 108, 110, 111, 112, 114, 115, 116, 117, 118, 119, 120
8. \(11 \cdots 47\)
9. 22.7
10.
| a. 11; 149 |
| b. 13; 3 · 7 · 13 |
| c. 19; 3 · 127 |
| d. 19; 19 · 23 |
| e. 19; 509 |
| f. 23; 613 |
| g. 23; 787 |
11.
| a.\(2 \cdots 2 \cdots 2 \cdots 5 \cdots 7\) |
| b. 281 |
| c.\(2 \cdots 3 \cdots 47\) |
| d. 283 |
| e.\(2 \cdots 2 \cdots 71\) |
| f.\(5 \cdots 3 \cdots 19\) |
| g.\(2 \cdots 11 \cdots 13\) |
| h.\(7 \cdots 41\) |
| i.\(25 \cdots 3 \cdots 3\) |
| j.\(17 \cdots 17\) |
| k.\(2 \cdots 5 \cdots 29\) |
| l.\(3 \cdots 97\) |
| m.\(2 \cdots 2 \cdots 73\) |
| n. 293 |
| o.\(2 \cdots 3 \cdots 7 \cdots 7\) |
| p.\(5 \cdots 59\) |
12. 281 y 283
13. No; al menos uno será un múltiplo de 3.
14.
| a. 1, 2, 3, 6, 7, 14, 42 |
| b. 1, 2, 5, 7, 10, 14, 35, 70 |
| c. 1, 2, 7, 14 |
| d. 14 |
| e. 14 |
15.
| a. 1, 2, 4, 23, 46, 92 |
| b. 1, 5, 23, 115 |
| c. 1, 23 |
| d. 23 |
| e. 23 |
16.
| a. 1, 2, 3, 4, 6, 8, 12, 16, 24, 48 |
| b. 1, 2, 3, 6, 9, 18, 27, 54 |
| c. 1, 3, 7, 9, 21, 63 |
| d. 1, 3 |
| e. 3 |
| f. 3 |
17.
| a. 14 | b. 23 | c. 3 |
| d. 34 | e. 25 | f. 42 |
18. a.\(24 \cdots 3 \cdots 132\)
19.
| a.\(2^{4} \cdots 3^{2} \cdots 7^{6} \cdots 13^{2}\) |
| b.\(3^{4} \cdots 5^{2}\) |
| c.\(a^{4} \cdots c^{3} \cdots d^{3} \cdots e^{2}\) |
| d.\(a^{2} \cdots d^{3}\) |
22. a. 2, 7
23. 1
24.
| a. m | b. 2m | c. m |
| d. 1 | e. m |
25. a - g: 1, 2, 3, 6
h. mismos factores
26. a - f: 6
27.
| a. 13 | b. 18 | c. 36 |
28.
| a. 38 r. 186 |
| b. 9 r. 33 |
| c. 7 r. 11 |
| d. 8 r. 25 |
29.
| a. 13 | b. 18 | c. 36 |
30. d. 22
31. d. 31
32. d. 1
34. 14|n si 2|n y 7|n.
35.
| a. Cierto desde 2|742 y 7|742 |
| b. Falso —7 no es un factor de 968 |
| c. Falso —2 no es un factor de 483 |
36. Piensa por qué TUS crees que no funciona. Esta es una pregunta que solo tú puedes responder.
37. Piensa por qué TÚ crees que funciona. Esta es una pregunta que solo tú puedes responder.
38.
| a. 4|n y 3|n |
| b. 9|n y 2|n |
39.
| a. 35|n si 5|n y 7|n |
| b. 28|n si 4|n y 7|n |
| c. 75|n si 3|n y 25|n |
| d. 56|n si 7|n y 8|n |
| e. c|n si 4|n, 27|n, 25|n y 11|n |
| f. d|n si 16|n, 3|n, 5|n y 11|n |
40.
| a - e. 1 |
| f. No; 1 es el factor más pequeño de cada número. |
Set de ejercicios 3 Soluciones
1.
| a. 8, 16, 24, 32, 40, 48, 56, 64, 72, 80 |
| b. 12, 24, 36, 48, 60, 72, 84, 96, 108, 120 |
| c. 24, 48, 72 |
| d. 24 |
| e. no |
2.
| a. 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60 |
| b. 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 66, 72, 78, 84, 90 |
| c. 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120, 130, 140, 150 |
| d. 60 |
| e. 60 |
5.
| a. X, Y |
| b. Y, Z |
| c. X, Y |
7. \(2^{2} \cdots 3^{5} \cdots 5 \cdots 7^{3} \cdots 11^{2} \cdots 1^{3}\)
8. \(2^{2} \cdots 3^{4} \cdots 7^{3} \cdots 11^{2} \cdots 13^{2} \cdots 1^{9}\)
9. \(2^{4} \cdots 3^{6} \cdots 5^{4} \cdots 7^{6} \cdots 11^{2} \cdots 1^{9} \cdots 23^{2}\)
10.
|
a. GCF:\(2^{2} \cdots 3^{2} \cdots 1^{3}\) LCM:\(2^{2} \cdots 3^{5} \cdots 5 \cdots 7^{3} \cdots 1^{3}\) |
|
b. GCF: 2 LCM:\(2^{2} \cdots 3^{4} \cdots 7^{3} \cdots 11^{2} \cdots 13^{2} \cdots 1^{9}\) |
|
c. GCF:\(c^{3} \cdots d\) LCM:\(a^{5} \cdots b^{4} \cdots c^{5} \cdots d^{3} \cdots e^{2}9\). |
|
d. GCF:\(c \cdots d\) LCM:\(a^{6} \cdots b^{4} \cdots c^{4} \cdots d^{3} \cdots e^{7}\) |
11.
| a. 120 |
| b. 1400 |
| c. 1274 |
| d. 840 |
| e. 1870 |
12.
| a. 3 · 2 · 2 · 7 · 3 · 5 = 1260 |
| b. 2·3·3·11·7·5·2·2·17 = 942,480 |
| c. 5·2·3·7·2·2·17·3·5 = 214,200 |
| d. 3 · 5 · 2 · 3 · 2 · 5 · 7 = 6,300 |
13. 14,112
14. 2,835
15. 3,705
16. 2 y 20; 4 y 10
17.
| a. 21 | b. 18.018 |
18.
| a. 73 | b. 74.095 |
19.
| a. 37 | b. 395.641 |
20.
| a. 6 | b. 58,344,300 |
25.
| a. 2 (4n + 10) es un número par. |
| b. 2 (5k + 4) + 1 es un número impar. |
| c. 5x + 2 puede ser par o impar |
26. Dejar 2n = un número par, y dejar 2m = otro número par. La suma es: 2n+2m = 2 (n+m), que es en forma de número par. Por lo tanto, la suma de 2 números pares es par.
27. Dejar 2n + 1 = un número impar, y dejar 2m + 1 = otro número impar. La suma es: 2n + 1 + 2m + 1 = 2n + 2m + 2 = 2 (n + m + 1), que está en forma de número par. Por lo tanto, la suma de 2 números impares es par
28. Dejar 2n = un número par, y dejar 2m + 1 = un número impar. La suma es: 2n + 2m + 1 = 2n + 2m + 1 = 2 (n + m) + 1, que es en forma de número impar. Por lo tanto, la suma de un número par y un número impar es impar.
29. Dejar 2n = un número par, y dejar 2m = otro número par. El producto es: 2n · 2m = 4mn = 2 (2mn), que está en forma de un número par. Por lo tanto, el producto de dos números pares es par.
30. Dejar 2n + 1 = un número impar, y dejar 2m + 1 = un número impar. El producto es: (2n + 1) (2m +) = 2nm + 2m + 2n + 1 = 2 (nm + m + n) + 1, el cual está en forma de número impar. Por lo tanto, el producto de dos números impares es impar.
31. Dejar 2n = un número par, y dejar 2m + 1 = un número impar. El producto es: 2n (2m + 1) = 4nm + 2n = 2 (2nm + n), que está en forma de número par. Por lo tanto, el producto de un número par y un número impar es par.
32. 3240
33. 3240
34. 31,375
35.
| a. 3,77 |
| b.148,181 |
| c.195,650 |
36.
| a. 3,775 |
| b. 148.181 |
| c. 195,650 |
| d. [n — (k —1)]\((n + k) \div 2\) o (n —k + 1)\((n + k) \div 2\) |
37. múltiplos de 7
38. 1 + 2 + 3 +. + 99 + 100
39.
| a. 5.050 |
| b. 5.050 |
| c. 35,350 |
40.
| a. 63.000 |
| b. 41.151 |
| c. 226,500 |
41. múltiplos de 4
42. 28 + 29 + 30 +. + 131 + 132
43. 33,600
44.
| a. 54.450 |
| b. 96.019 |
45. 6
46. 4, 8, 14
47. 4, 6
48. 4
49. 8
50. 3, 7
51. 7
52. 68, 178, 288, 398, 508, 618, 728, 838, 948
53. 5
54. 5
55. 5 ó 26
56. mult. de 7
57. 9 ó 23
58. 3, 5 o 9
59. 9
60. Sí; explicación no proporcionada aquí
Soluciones para la tarea
1. GCF:14; LCM: 6.300
3. a. GCF: 47; MCM: 49,350
4. a. Dado que el número es par, solo necesitamos hacer que el número resultante sea divisible por 3. La raíz digital hasta el momento es 8. Entonces, decide qué dígitos individuales podrían agregarse a 8 para obtener un número que sigue siendo divisible por 3. Agregar 1, 4 o 7 a 8 funcionará. Entonces las posibilidades son 4, 7 u 8.
5. Los ejemplos y contraejemplos no son proporcionados por estas soluciones. ¡Asegúrate de proporcionarlos!
| a. falso |
| b. verdadero |
6.
| a.\(7 \cdots 53\) |
| d.\(7 \cdots 41\) |
7.
| a. m |
| b. m |
| c. m |
| d. 1 |
9.
| a. 49,770 |
| b. 35.800 |
10.
| a. 39 |
| b. 80 |
11.
| a. 1, 2, 3; 6; perfecto |
| b. 1; 1; deficiente |
| c. 1, 2, 4; 7; deficiente |
13. Aquí no se proporcionan ejemplos y contraejemplos. Asegúrate de proporcionarlos.
| a. Falso |
| b. Cierto |
| c. Falso |
| d. Cierto |
15. a. 84
Módulo 9 Números racionales
Soluciones de calentamiento
1. R
2. Y
3. P
4. D
5. O
6. D
7. H
8. B
9. D
10. O
11. Y
12. B
13. B
14. L
Set de ejercicios 1 Soluciones
1. \(\frac{1}{12} < \frac{1}{10} < \frac{1}{9} < \frac{1}{8} < \frac{1}{6} < \frac{1}{5} < \frac{1}{4} < \frac{1}{3} < \frac{1}{2}\)
2.
| a.\(\frac{1}{90}\) | b.\(\frac{1}{32}\) |
3. \(\frac{5}{12} < \frac{5}{10} < \frac{5}{9} < \frac{5}{8} < \frac{5}{6}\)
4.
| a.\(\frac{15}{37}\) | b.\(\frac{89}{100}\) |
5. \(\frac{4}{12} < \frac{4}{11} < \frac{4}{10} < \frac{4}{9} < \frac{4}{8} < \frac{4}{7} < \frac{4}{6} < \frac{4}{5}\)
6. Si estás comparando dos fracciones que tienen el mismo numerador, la que tiene el denominador más pequeño tiene el valor mayor.
7, 8. \(\frac{1}{2} < \frac{2}{3} < \frac{3}{4} < \frac{4}{5} < \frac{5}{6} < \frac{7}{8} < \frac{8}{9} < \frac{9}{10} < \frac{11}{12}\)
9.
| a.\(\frac{94}{95}\) | b.\(\frac{89}{100}\) |
10. \(\frac{13}{14} < \frac{25}{26} < \frac{34}{35} <\frac{45}{46} < \frac{51}{52} < \frac{71}{72} < \frac{99}{100}\)
11. Si estás comparando dos fracciones donde en cada fracción el numerador es uno menos que el denominador, la fracción con el numerador mayor y denominador tiene el valor mayor.
12. Las respuestas variarán. Intenta dibujar un pastel por cada fracción, sombreando en 2 de 3 partes iguales para 2/3 y 4 de 5 partes iguales para 4/5. ¿Qué pastel está más sombreado?
13. Las respuestas variarán
14. \(\frac{2}{4}\)y\(\frac{3}{6}\) y\(\frac{4}{8}\) y\(\frac{5}{10}\) y\(\frac{6}{12}\)
15. \(\frac{4}{6}\)y\(\frac{6}{9}\) y\(\frac{8}{12}\)
16 - 17: Hay muchas posibilidades usando múltiples tiras.
18. Multiplica el numerador y denominador por el mismo número para obtener una fracción equivalente.
19 - 27. A continuación solo se muestran las respuestas finales. Haz tus propios modelos para los ejercicios 22 - 28 siguiendo los ejemplos asegurándote de mostrar todos los pasos, definir unidades, filas, columnas, etc.
19. \(\frac{3}{4} < \frac{4}{5}\)
20. \(\frac{13}{20}\)
21. \(\frac{5}{24}\)
22.
| a.\(\frac{8}{15}\) | b.\(\frac{15}{24}\) |
23.
| a.\(\frac{2}{3} \cdots \frac{5}{6} = \frac{10}{18}\) | b.\(\frac{1}{2} \cdots \frac{7}{8} = \frac{7}{16}\) |
24.
| a.\(\frac{4}{5} \cdots \frac{3}{5} = \frac{12}{25}\) | b.\(\frac{1}{7} \cdots \frac{3}{4} = \frac{3}{28}\) |
25. Las respuestas pueden variar. Una posibilidad: Let 1 = H;\(\frac{3}{4}\) de H = B;\(\frac{1}{3}\) de B = L;\(\frac{L}{H} = \frac{3}{12}\)
26.
| a. H; B; L; L/H; 3/12 |
| b. N; R; W; W/N; 1/8 |
| c. N; R; L; L/N; 3/8 |
| d. D; L; R; R/D; 2/6 |
27 - 30. Haz tus propios modelos. Se da una posibilidad para cada uno usando el modelo de tira C, pero hay otras opciones.
27. Dejar 1 unidad = O, luego 1/10 = W y 1/5 = R. Hay 2 W en R, entonces la respuesta es 2.
28. Dejar 1 unidad = B, luego 1/9 = W y 1/3 = L. Hay 3 W en L, entonces la respuesta es 3.
29. Dejar 1 unidad = H, luego 1/6 = R y 2/3 = N. Hay 4 R en N, entonces la respuesta es 4.
30. Dejar 1 unidad = P, luego 1/4 = W y 3 = H. Hay 12 W en H, entonces la respuesta es 12.
31.
| a. equivalente | b. equivalente | c. no equivalente |
32. Hay infinitamente muchas posibilidades: puedes usar las múltiples tiras para encontrar algunas.
33. igual que #31
34.
| a.\(\frac{14}{25}\) | b.\(\frac{13}{17}\) | c.\(\frac{18}{35}\) | d.\(\frac{15}{22}\) |
35. igual que #31
36.
| a.\(\frac{4}{5} > \frac{5}{8}\) | b.\(\frac{12}{35} < \frac{11}{18}\) | c.\(\frac{13}{15} > \frac{14}{17}\) |
37. \(89 \cdots 95 < 90 \cdots 94\)desde 8455 < 8460. Comprobación cruzada de productos.
38. Se comprueba, muestra el trabajo
39.
| a. -4/70 | b. 71/72 |
40. Las respuestas pueden variar. Algunas posibilidades: 21/50, 22/50, 23/50,., 29/50
41,42. 1/2
43. Algunas posibilidades: 51/150, 52/150, 53/150,., 59/150
44. Algunas posibilidades: 21/60, 22/60, 23/60,., 29/60
45. 241/300, 242/300, 243/300,., 249/300
46. 83/112
47. 75/112
48. Dibuja 12 círculos. 11 de los círculos suman 66, así que pon 6 en cada círculo. Respuesta: 6 alumnos.
49. Dibuja 7 círculos, ya que 3 círculos suman 36, pon 12 en cada círculo. Los otros 4 círculos representan a los estudiantes que no compran el almuerzo. Respuesta: 48 alumnos
50. Dibuja 8 círculos. Dado que los 8 círculos suman 120, ponen 15 en cada círculo. 5 de los círculos representan a las hembras, los otros tres representan a los machos. Respuesta: 75 hembras y 45 machos.
Set de ejercicios 2 Soluciones
1.
| a. cuatro décimas;\(\frac{4}{10} = \frac{2}{5}\) |
| b. veintiséis centésimas;\(\frac{26}{100} = \frac{13}{50}\) |
| c. tres y ocho centésimas;\(3\frac{8}{100} = 3\frac{2}{25}\);\(\frac{388}{100} = \frac{77}{25}\) |
| d. nueve y ochenta y cinco centésimas;\(9\frac{85}{100} = 9\frac{17}{20}\);\(\frac{985}{100} = \frac{197}{20}\) |
| e. diecisiete trescientos cinco milésimas;\(17\frac{305}{1000}= 17\frac{61}{200}\);\(\frac{17305}{1000} = \frac{3461}{200}\) |
2.
| a. 0.14 | b. 008 |
| c. 4\(\frac{35}{100} = 4.35\) | d. 563\(\frac{8}{10} = 563.8\) |
| e. 3\(\frac{5}{100} = 3.05\) |
3.
| a. 0.028 | b. 0.32 |
| c. 0.075 | d. 0.66 |
4.
| a. 1.9; 1.90000 |
| b. 4.0340 |
5.
| a. 3.5 > .9 |
| b. 35.06 = 3.0600 |
| c. 0.089 < 0.0908 |
6.
| a. 3.51 > 3.488 |
| b. 35.061 < 35.35 |
| c. 0.8933 < 0.0894 |
7.
| a.\(2 \cdots 5\) | b.\(2 \cdots 5 \cdots 2 \cdots 5\) |
| c.\(2 \cdots 5 \cdots 2 \cdots 5 \cdots 2 \cdots 5\) | d.\(2 \cdots 5 \cdots 2 \cdots 5 \cdots 2 \cdots 5 \cdots 2 \cdots 5\) |
| e.\(2 \cdots 5 \cdots 2 \cdots 5 \cdots 2 \cdots 5 \cdots 2 \cdots 5 \cdots 2 \cdots 5\) |
8. 2 y 5
9. 3
10. 2
11. Bueno, ¿qué opinas?
12.
| a. 0.0875 | b. 0.875 |
13. Escribe una respuesta con tus propias palabras.
14.
| a.\(\frac{3}{4} = \frac{3}{2 \cdots 2} \cdots \frac{5 \cdots 5}{5 \cdots 5} = \frac{75}{100} = 0.75\) |
| b.\(\frac{9}{20} = \frac{3 \cdots 3}{2 \cdots 2 \cdots 5} \cdots \frac{5}{5} = \frac{45}{100} = 0.45\) |
| c.\(\frac{9}{15} = \frac{3 \cdots 3}{3 \cdots 5} = \frac{3}{5} \cdots \frac{2}{2} = \frac{6}{10} = 0.6\) |
| d.\(\frac{18}{25} = \frac{2 \cdots 3 \cdots 3}{5 \cdots 5} \cdots \frac{2 \cdots 2}{2 \cdots 2} = \frac{72}{100} = 0.72}\) |
| e.\(\frac{5}{14} = \frac{5}{2 \cdots 7}\) Esto no se puede escribir como decimal de terminación porque el factor reducido tiene un factor primo de 7 (que es distinto de un 2 o 5) en el denominador. |
15. Haz tres de los tuyas.
16.
| a. 0, 1, 2, 3, 4, 5 |
| b. 0, 1, 2, 3, 4, 5, 6 |
| c. 0, 1, 2, 3, 4, 5, 6, 7, 8 |
| d. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 |
| e. 0, 1, 2 |
17. Haz tres de los tuyas.
18. a, b, d
19.
| a. Hay 33 (incluyendo 0 como resto). Un máximo de 32 dígitos podría estar en una secuencia sin repetir. |
| b. si haces la división larga, obtienes .939393... |
| c. 2 |
| d. 13 y 31 |
20.
| a. 0. \(\bar{5}\)o 0.555... |
| b. 0. \(\bar{714285}\)o 0.714285714285... |
| c. 0.1\(\bar{6}\) ó 0.1666... |
| d. 0. \(\bar{6}\)o 0.666.. |
| e. 0. \(\bar{63}\)o 0.636363... |
| f. 0.41\(\bar{6}\) o 0.41666.. |
| g. 0.5\(\bar{3}\) ó 0.5333... |
| h. 0.3\(\bar{5}\) ó 0.3555... |
| i. 0.0\(\bar{75}\) ó 0.0757575... |
21. x - 1
22.
10x = 7.272727... ;
100x = 72.727272... ;
1000x = 727.272727...
23.
| a. 99x |
| b. 72 |
| c. 99x = 72; x =\(\frac{72}{99}\) |
| d. x =\(\frac{8}{11}\) |
24.
| a.\(\frac{4}{10} =\frac{2}{5}\) | b.\(\bar{4} = \frac{4}{9}\) |
| c.\(\frac{6}{100} = \frac{3}{50}\) | d.\(\bar{0.06} = \frac{6}{99} = \frac{2}{33}\) |
| e.\(\frac{9}{10}\) | f.\(\bar{0.9} = \frac{9}{9} = 1\) sorpresa! |
| g.\(\frac{45}{100} = \frac{9}{20}\) | h. 0. \(\bar{45} = \frac{45}{99} = \frac{5}{11}\) |
| i.\(\frac{84}{1000} = \frac{21}{250}\) | j. 0. \(\bar{084} = \frac{84}{999} = \frac{28}{333}\) |
25.
| a.\(\frac{2.8}{99} = \frac{28}{99 \cdots 10} = \frac{14}{495}\) |
| b.\(\frac{2.6}{9} = \frac{26}{9 \cdots 10} = \frac{13}{45}\) |
| c.\(\frac{0.06}{9} = \frac{6}{9 \cdots 100} = \frac{1}{150}\) |
| d.\(\frac{101}{999}\) |
| e.\(\frac{3.6}{9} = \frac{36}{9 \cdots 10} = \frac{2}{5}\) |
26. ¡Sé creativo!
27. No, ya que el 9 es un cuadrado perfecto. Entonces,\(\sqrt{9} = 3\)
28-30. ¡Sé creativo!
31.
| a. racional (repetición decimal). |
| b. irracional (¡tiene un patrón, pero no se repite!) |
| c. racional |
| d. irracional (ya que 80 no es un cuadrado perfecto) |
| e. racional (ya que 100 es un cuadrado perfecto; entonces\(\sqrt{100} = 10\) |
| f. irracional |
Soluciones para la tarea
1.
| a. K | c. D | e. D | g. h |
2.
| a. H | c. P | e. R |
3. a. L
7. \(\frac{1}{3} < \frac{3}{8}\)
8. \(\frac{17}{24}\)
9. \(\frac{7}{20}\)
10. a.\(\frac{3}{20}\)
11. a.\(\frac{5}{6} \cdots \frac{2}{3} = \frac{10}{18}\)
12. a.\(\frac{2}{3} \cdots \frac{3}{8} = \frac{6}{24}\)
13. a. B; D; R; R/B; 2/9
14. a. 15
16. a.\(\frac{18}{35}\)
18. Algunas posibilidades: 31/80, 32/80, 33/80,., 49/80
20. a. Dibuja 10 círculos. Ya que 7 de los círculos suman 21, pon 3 en cada círculo. Los 10 círculos suman 30, por lo que hay 30 alumnos.
21.
| a. siete décimas |
| b. tres y veintiocho centésimas |
22.
| a.\(\frac{3}{10} \cdots \frac{8}{10} = \frac{14}{100} = 0.14\) |
| b.\(\frac{122}{100} \cdots \frac{23}{10} = \frac{2086}{1000} = 2.806\) |
23.
| a.\(\frac{11}{16} = \frac{11}{2 \cdots 2 \cdots 2 \cdots 2} \cdots \frac{5 \cdots 5 \cdots 5 \cdots 5}{5 \cdots 5 \cdots 5 \cdots 5} = \frac{6875}{10000} = 0.6875\) |
| c.\(\frac{1}{12} = \frac{1}{2 \cdots 2 \cdots 3}\) |
Esto no se puede escribir como un decimal de terminación porque el factor reducido tiene un factor primo de 3 (que es distinto de un 2 o 5. en el denominador).
24.
| a.\(\frac{7}{9}\) | c.\(\frac{235}{999}\) |

