16.3: Diagramas Tanabe-Sugano

Introducción

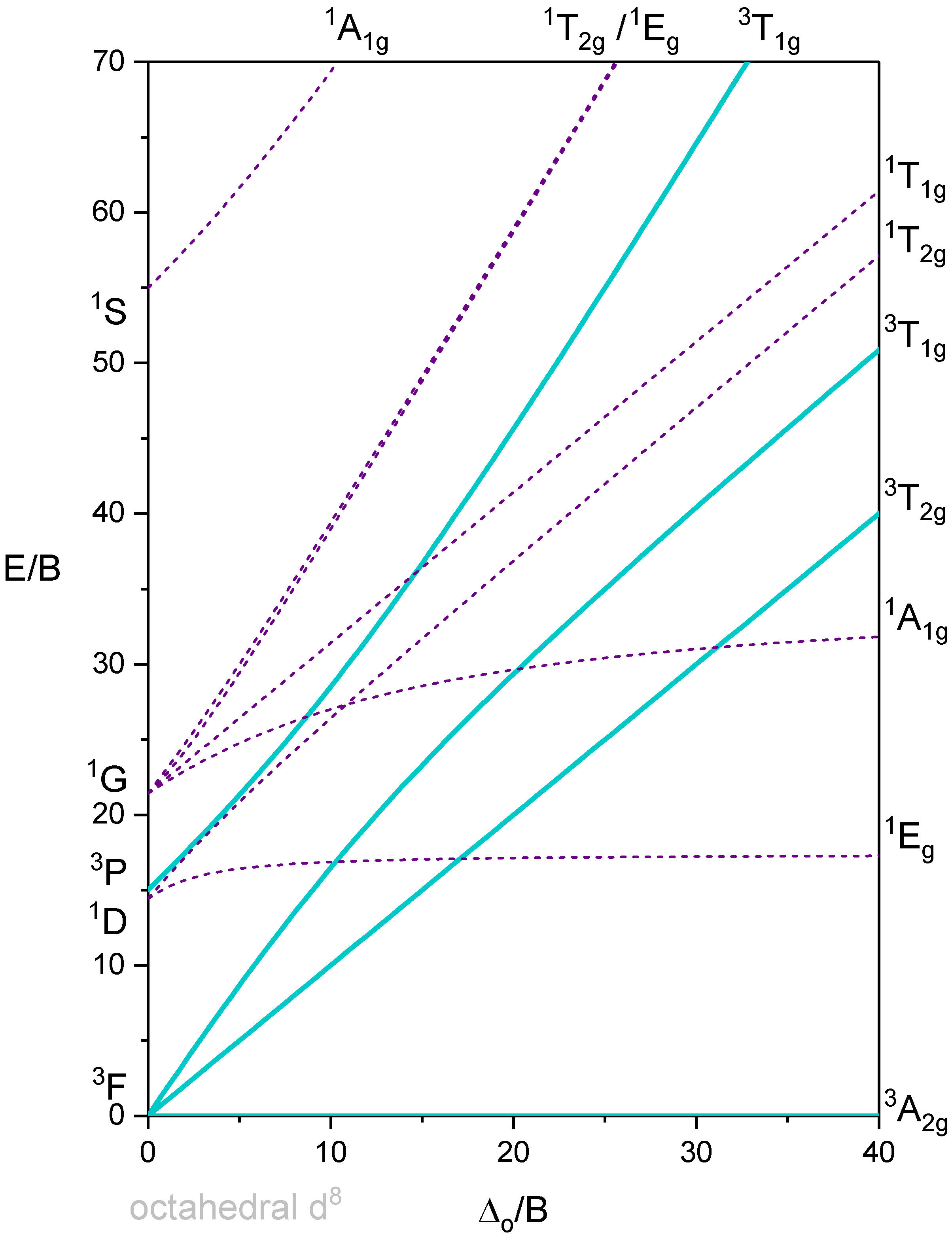
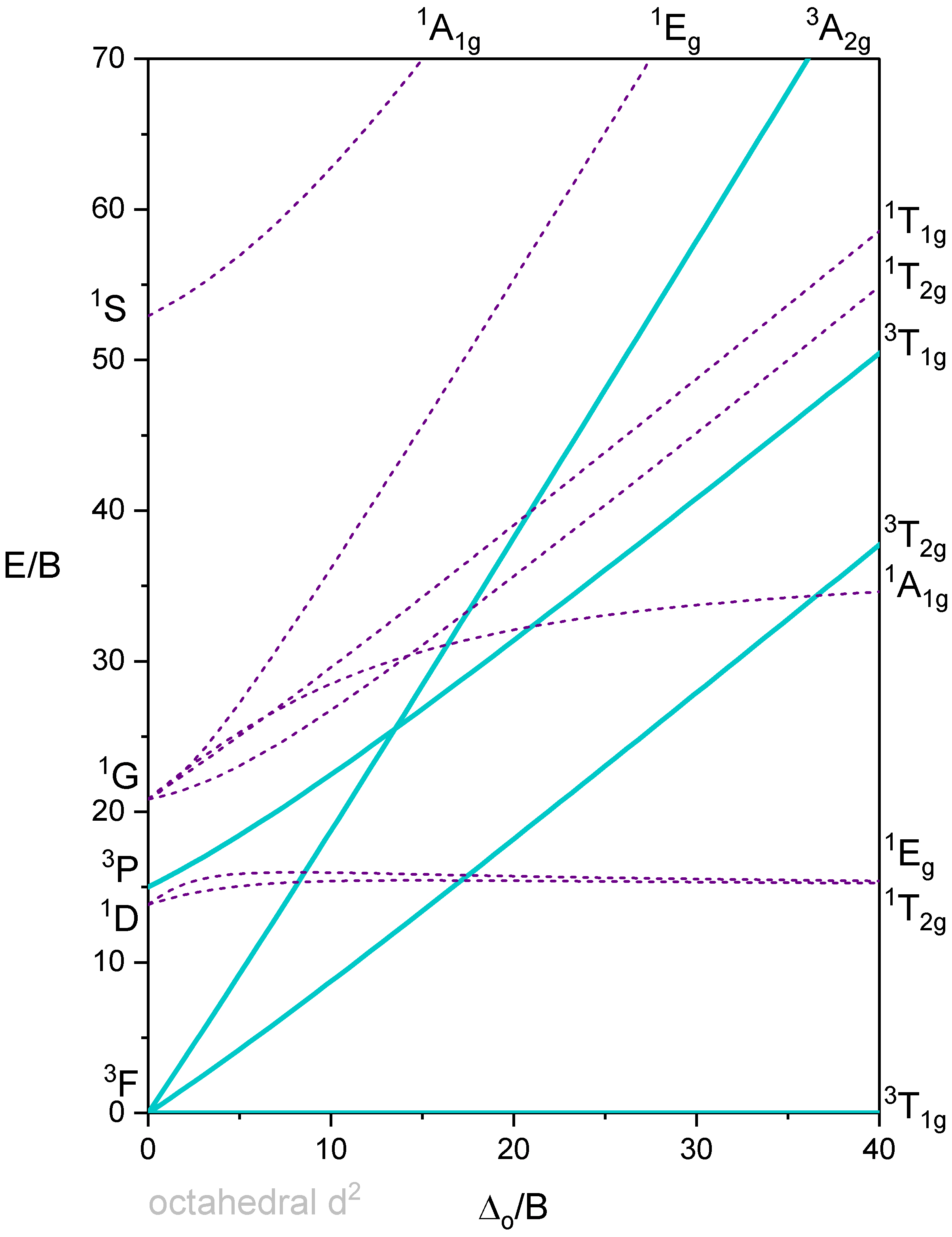
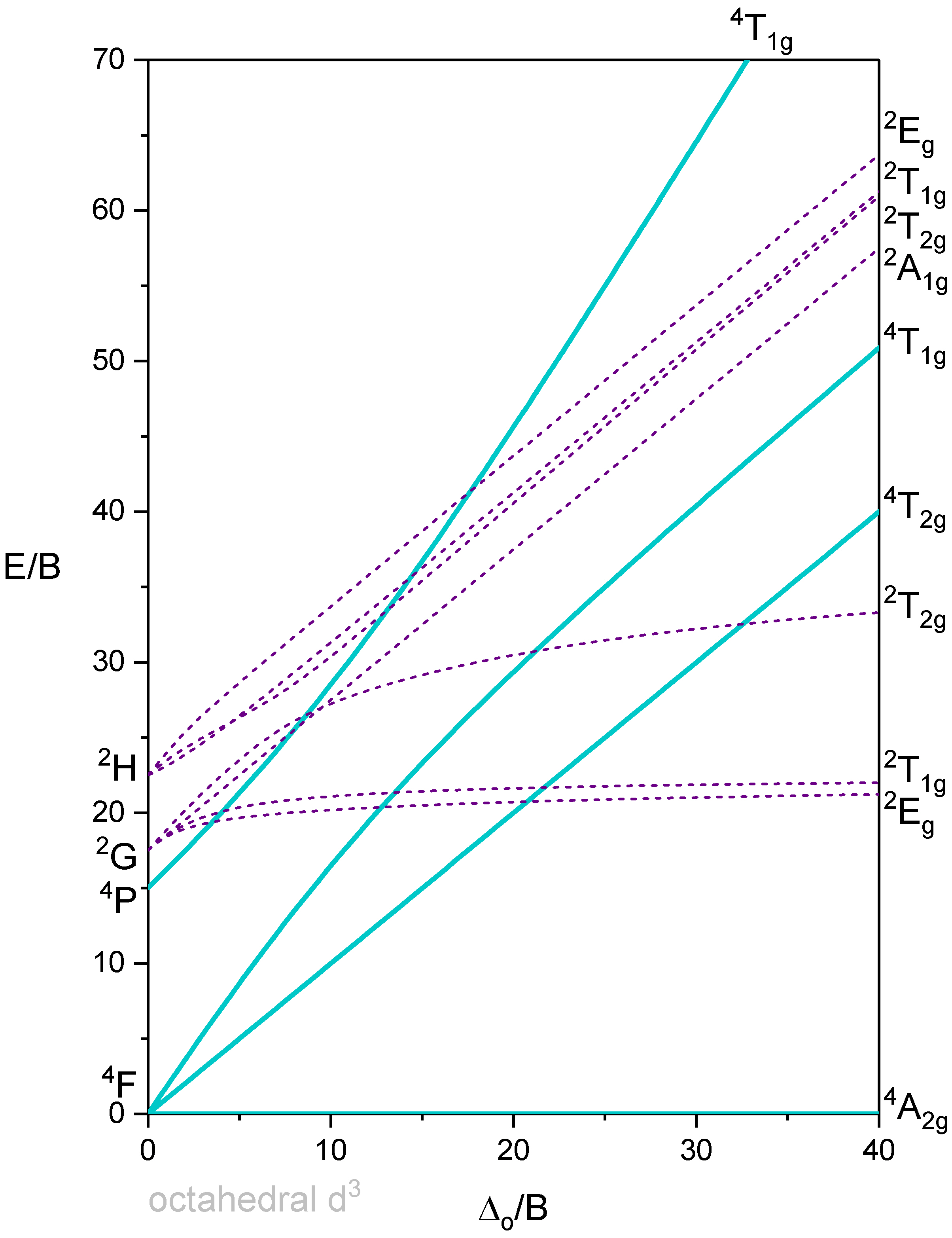
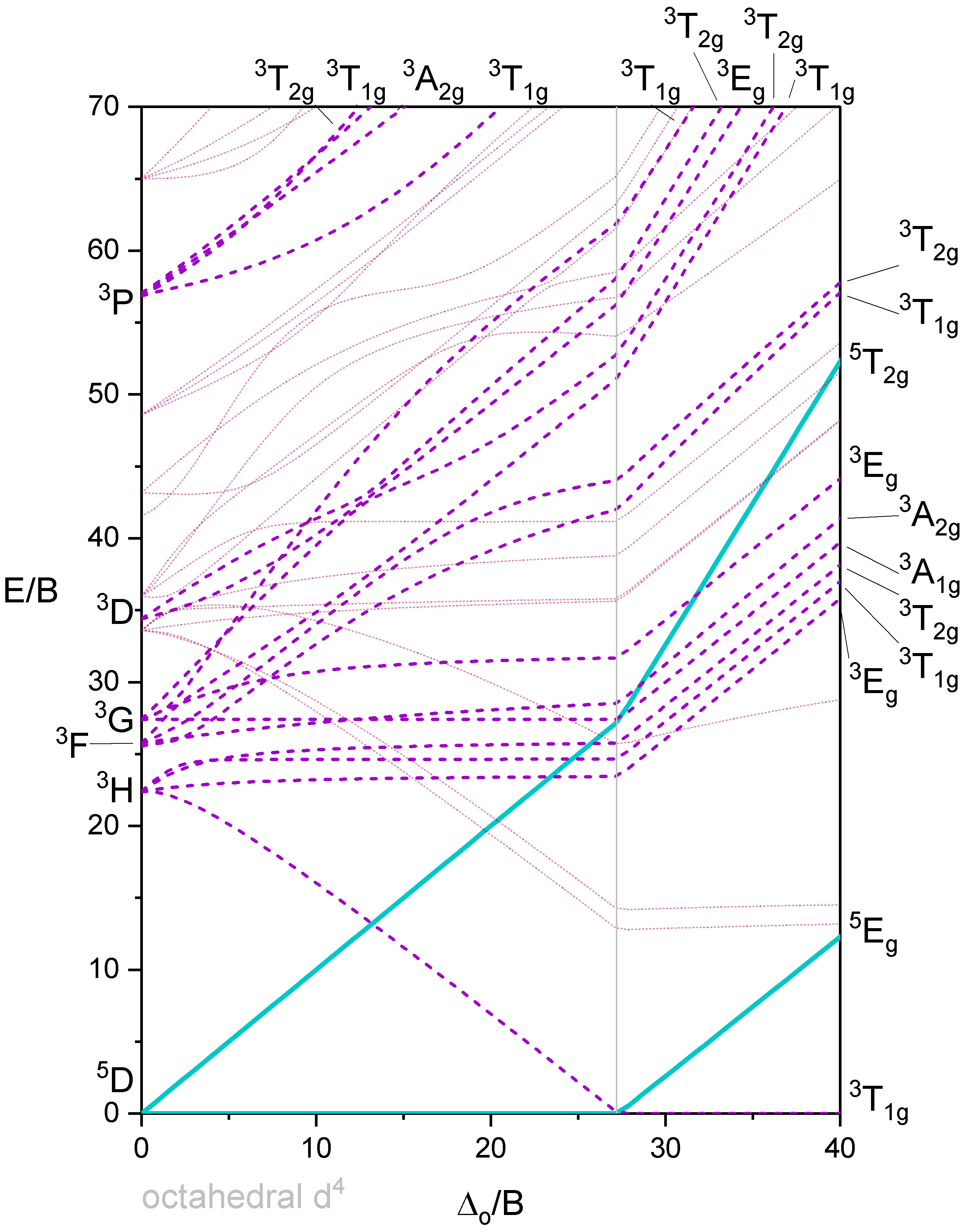
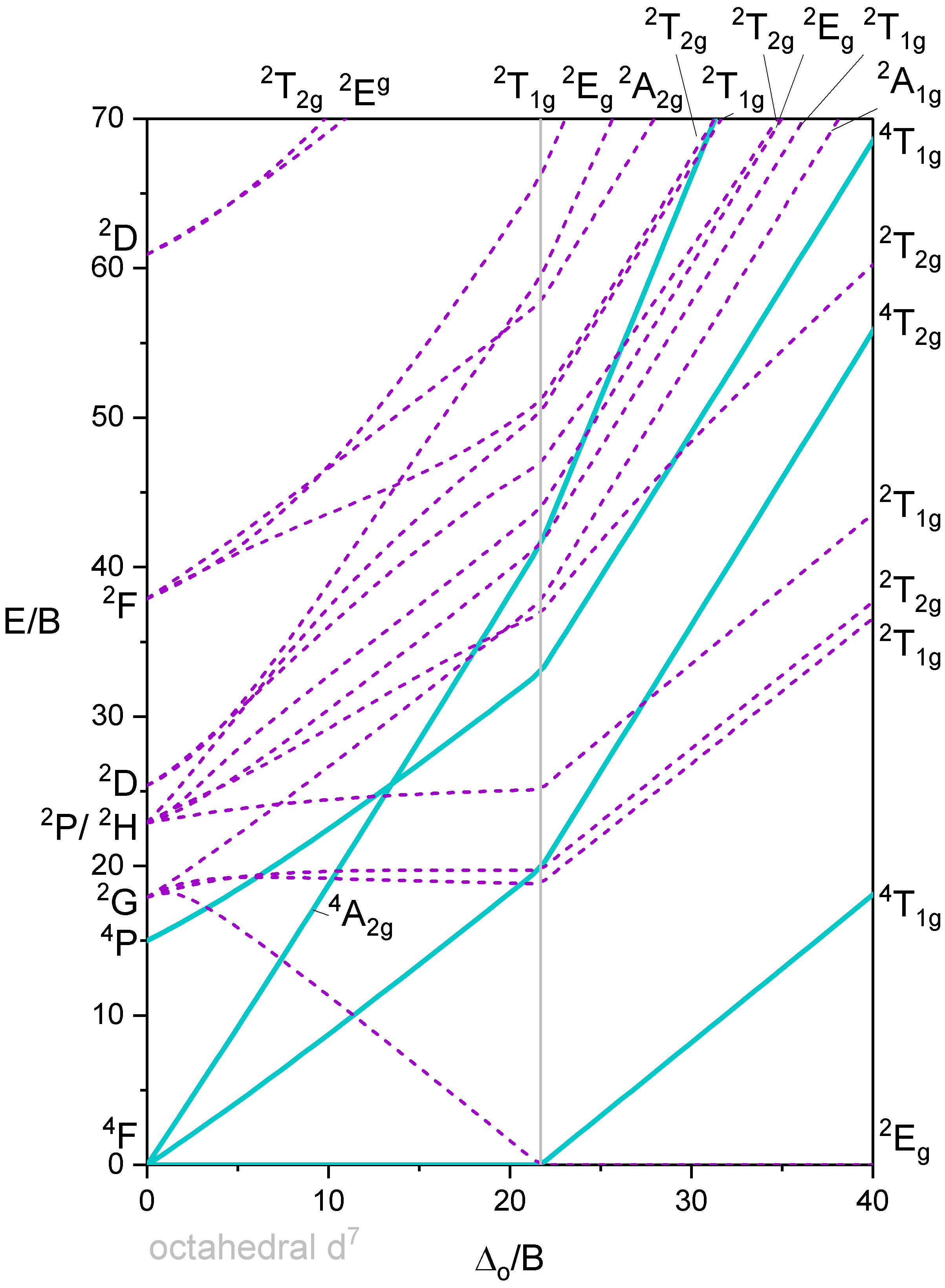
Los diagramas Tanabe-Sugano son una forma de diagramas de correlación. Estos diagramas muestran las energías relativas de términos (por ejemplo, microestados electrónicos) trazando la energía de división y la intensidad de campo en términos del Parámetro de Racah, B (trazado como\(\frac{E}{B}\) vs\(\frac{\Delta}{B}\)). El parámetro Racah da cuenta de las repulsiones\(d\) -electrón-electrón que afectan las energías de los términos (y por lo tanto la energía de transición). Estos diagramas son útiles para interpretar espectros electrónicos. Específicamente, los diagramas pueden usarse para predecir cualitativamente el número de transiciones permitidas y prohibidas por giro, las intensidades relativas de estas transiciones y sus energías relativas. Los diagramas también se pueden utilizar para estimar la energía\(d\) de división orbital (\( \Delta\)o\(10 D_q \)) y la intensidad de campo necesaria para causar la transición entre alta y baja espín.

Los diagramas Tanabe-Sugano que se muestran a continuación pueden ser utilizados para interpretar los espectros de complejos octaédricos de una configuración electrónica dada. Los diagramas para los complejos octaédricos para\(d^2, \; d^3, \; d^4, \; d^5, \;  d^6,  \; d^7\) y\(d^8\) se dan a continuación. Los diagramas Tanabe-Sugano para\(d^0,  \; d^1,  \; d^9\) y\(d^{10}\) son innecesarios. En el caso de\(d^0\) y\(d^{10}\), no hay\(d-d\) transiciones posibles porque los\(d\) -orbitales están completamente vacíos o completamente llenos. En el caso de\(d^1\), sólo hay un término de iones libres (\(^2D\)) que se divide en un estado fundamental\(^2T_{2g}\) y estado excitado\(^2E_g\). No hay repulsiones electrón-electrón a considerar, y solo hay una transición posible, por lo que el diagrama Tanabe-Sugano es innecesario para\(d^1\). El caso de\(d^9\) es similar y está relacionado con\(d^1\) el concepto de “agujero positivo”. En el caso de\(d^9\), el término de iones\(^2D\) libres solitarios se divide en un término de estado fundamental y un\(^2E_g\) término de estado\(^2T_{2g}\) excitado. Solo hay una transición posible y así el diagrama Tanabe-Sugano para también\(d^9\) es innecesario. En algunos casos, se dan dos versiones; una versión completa y una versión simplificada. Todos los diagramas se muestran en tamaño de página completa.

Estos diagramas también pueden ser utilizados para interpretar los espectros electrónicos de complejos tetraédricos. Para un complejo tetraédrico con\(d^m\), use el diagrama que se da a continuación para\(d^{10-m}\). Todos los subíndices\(g\) "" en los términos son irrelevantes para los tetraedros.

Octaedro con 2 electrones d

Figura\(\PageIndex{2}\):\(d^2\): Diagrama Tanabe-Sugano para el complejo metálico octaédrico con dos\(d\) electrones. Para mayor comodidad, los términos que pueden acomodar transiciones permitidas por giro desde el estado fundamental se indican mediante líneas continuas. Los términos que tienen multiplicidad diferente al estado fundamental se muestran en líneas discontinuas. (CC-BY-SA; Kathryn Haas)

 

Octaedro con 3 electrones d

Figura\(\PageIndex{2}\):\(d^3\): Diagrama Tanabe-Sugano para el complejo metálico octaédrico con tres\(d\) electrones. Para mayor comodidad, los términos que pueden acomodar transiciones permitidas por giro desde el estado fundamental se indican mediante líneas continuas. Los términos que tienen multiplicidad diferente al estado fundamental se muestran en líneas discontinuas. (CC-BY-SA; Kathryn Haas)

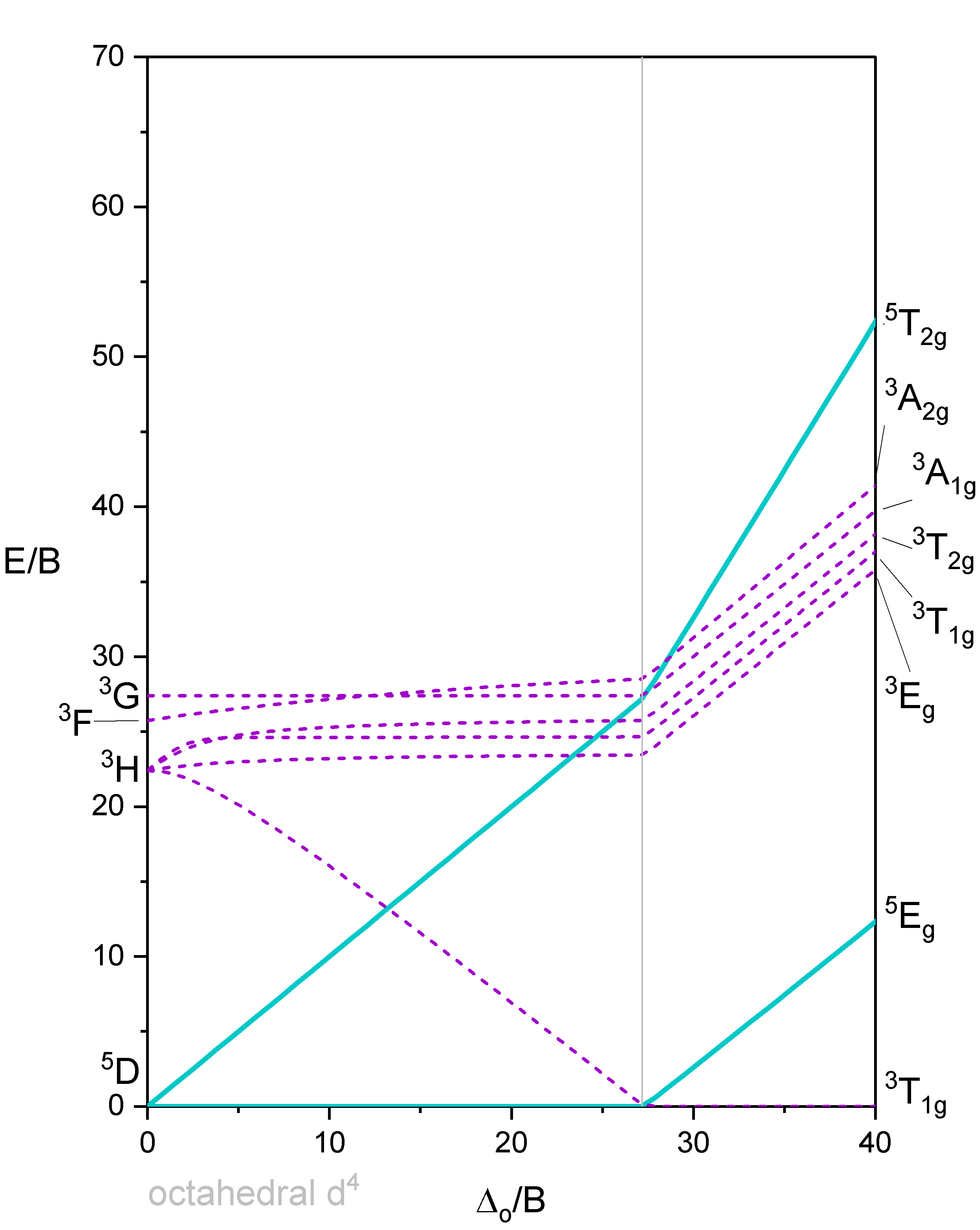
Octaedro con 4 electrones d

La Figura 3 muestra un diagrama de Tanabe-Sugano que incluye todos los términos. A continuación se muestra una versión simplificada del Diagrama\(d^4\) Tanabe-Sugano en la Figura 4.

Figura\(\PageIndex{3}\):\(d^4\), completo: Diagrama Tanabe-Sugano para el complejo metálico octaédrico con cuatro\(d\) electrones. Una línea vertical gris en 27.2\(\frac{\Delta_o}{B}\) divide los casos de alto giro de los casos de giro bajo. Para mayor comodidad, los términos que pueden acomodar transiciones permitidas por giro desde el estado fundamental del pentet en alto giro (izquierda de la línea gris) se indican mediante líneas sólidas pesadas. Los términos que pueden acomodar transiciones permitidas por giro desde el estado fundamental del triplete de giro bajo se muestran en líneas discontinuas pesadas. Los términos que tienen multiplicidad diferente a los estados de tierra penteta o triplete se muestran en líneas punteadas más claras. Para una versión simplificada del\(d^4\) diagrama, consulte la Figura\(\PageIndex{4}\). (CC-BY-SA; Kathryn Haas)

Figura\(\PageIndex{4}\):\(d^4\), simplificado: Diagrama Tanabe-Sugano para el complejo metálico octaédrico con cuatro\(d\) electrones. Una línea vertical gris en 27.2\(\frac{\Delta_o}{B}\) divide los casos de alto giro de los casos de giro bajo. Para mayor comodidad, los términos que pueden acomodar transiciones permitidas por giro desde el estado fundamental del pentet en alto giro (izquierda de la línea gris) se indican mediante líneas sólidas pesadas. Los términos que pueden acomodar transiciones permitidas por giro desde el estado fundamental del triplete de giro bajo se muestran en líneas discontinuas pesadas. Esta versión del Diagrama\(d^4\) Tanabe Sugano se abrevia en el sentido de que solo muestra los términos de aleación de espín que son más relevantes para interpretar los espectros UV-Visible. Para ver la versión completa de un\(d^4\) diagrama, consulte la Figura\(\PageIndex{3}\). (CC-BY-SA; Kathryn Haas)

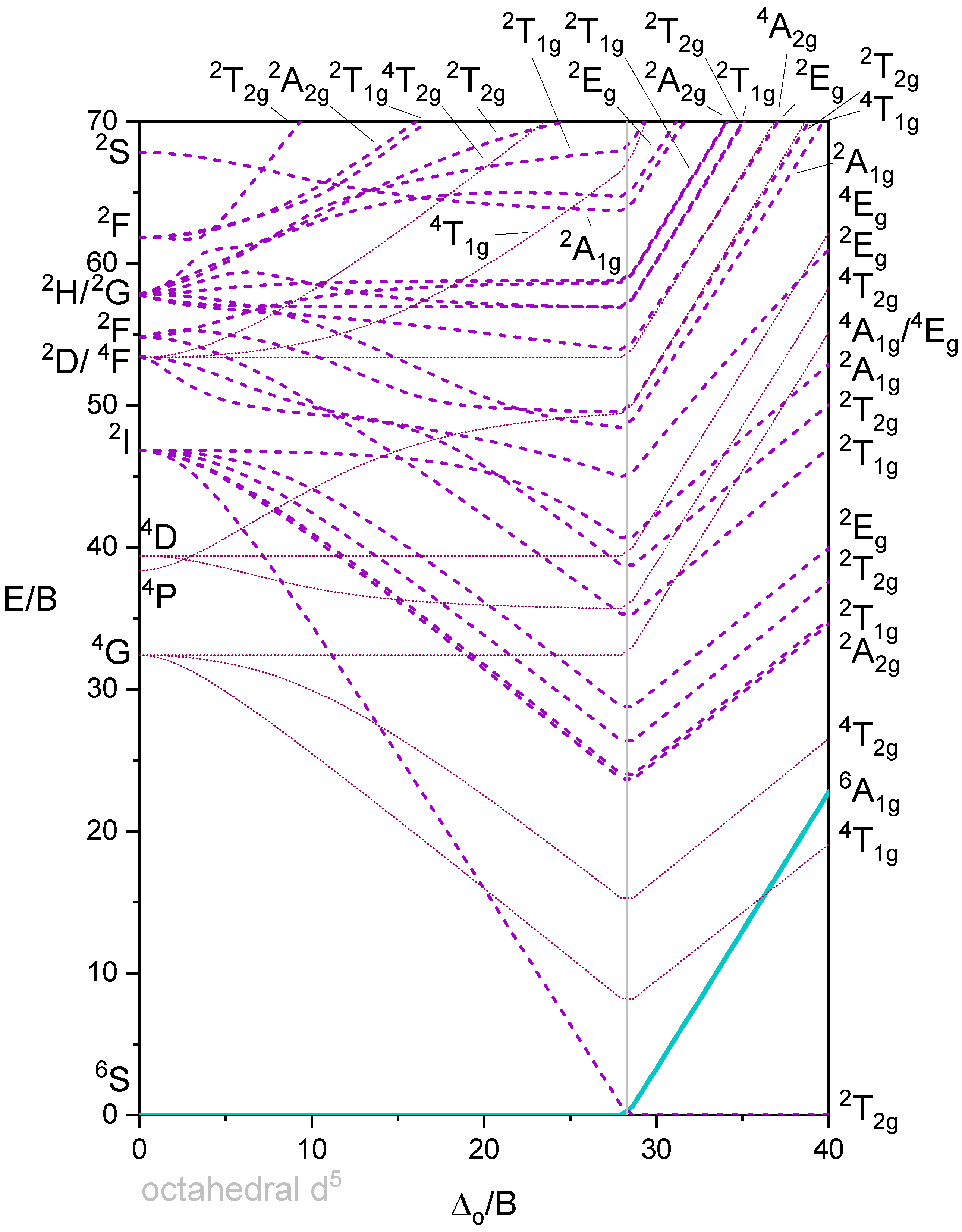
Octaedro con 5 electrones d

La Figura 5 muestra un diagrama de Tanabe-Sugano que incluye todos los términos. A continuación se muestra una versión simplificada del Diagrama\(d^5\) Tanabe-Sugano en la Figura 6.

Figura\(\PageIndex{5}\):\(d^5\), completo: Diagrama Tanabe-Sugano para el complejo metálico octaédrico con cinco\(d\) electrones. Una línea vertical gris en 27.3\(\frac{\Delta_o}{B}\) divide los casos de alto giro de los casos de giro bajo. Para mayor comodidad, los términos que pueden acomodar transiciones permitidas por giro desde el estado fundamental del sexteto en alto giro (izquierda de la línea gris) se indican mediante líneas continuas pesadas. Los términos que pueden acomodar transiciones permitidas por giro desde el estado fundamental del doblete de giro bajo se muestran en líneas discontinuas pesadas. Los términos que tienen multiplicidad diferente a los estados del suelo se muestran en líneas punteadas más claras. Para una versión simplificada del\(d^5\) diagrama, consulte la Figura\(\PageIndex{6}\). (CC-BY-SA; Kathryn Haas)

Figura\(\PageIndex{6}\):\(d^5\), simple: Diagrama Tanabe-Sugano para el complejo metálico octaédrico con cinco\(d\) electrones. Una línea vertical gris en 27.3\(\frac{\Delta_o}{B}\) divide los casos de alto giro de los casos de giro bajo. Para mayor comodidad, los términos que pueden acomodar transiciones permitidas por giro desde el estado fundamental del sexteto en alto giro (izquierda de la línea gris) se indican mediante líneas continuas pesadas. Los términos que pueden acomodar transiciones permitidas por giro desde el estado fundamental del doblete de giro bajo se muestran en líneas discontinuas pesadas. Los términos que tienen multiplicidad diferente a los estados del suelo se muestran en líneas punteadas más claras. Esta versión del Diagrama\(d^5\) Tanabe Sugano se abrevia por simplicidad y con el propósito de interpretar los espectros UV-Visible. Para la versión completa de un\(d^5\) diagrama, ver Figura\(\PageIndex{5}\) (CC-BY-SA; Kathryn Haas)

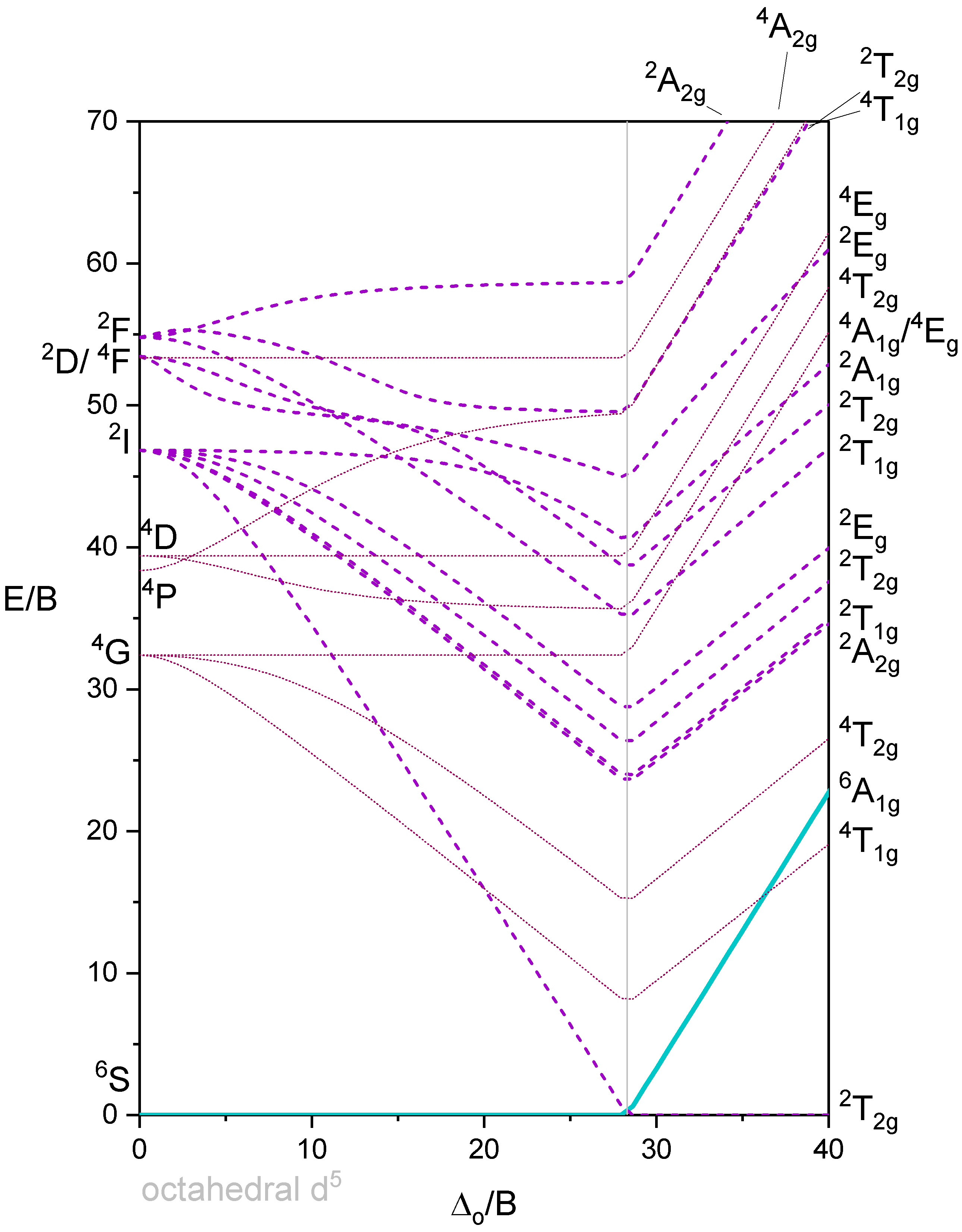
Octaedro con 6 electrones d

Figura\(\PageIndex{7}\)\(d^6\): Diagrama Tanabe-Sugano para el complejo metálico octaédrico con seis\(d\) electrones. Una línea vertical gris a 18.5\(\frac{\Delta_o}{B}\) divide el giro alto de los casos de giro bajo. Para mayor comodidad, los términos que pueden acomodar transiciones permitidas por giro desde el estado fundamental del pentet en alto giro (izquierda de la línea gris) se indican mediante líneas sólidas pesadas. Los términos que pueden acomodar transiciones permitidas por giro desde el estado fundamental del singlete de giro bajo se muestran en líneas discontinuas pesadas. Los términos que tienen multiplicidad diferente a los estados del suelo se muestran en líneas punteadas más claras. (CC-BY-SA; Kathryn Haas)

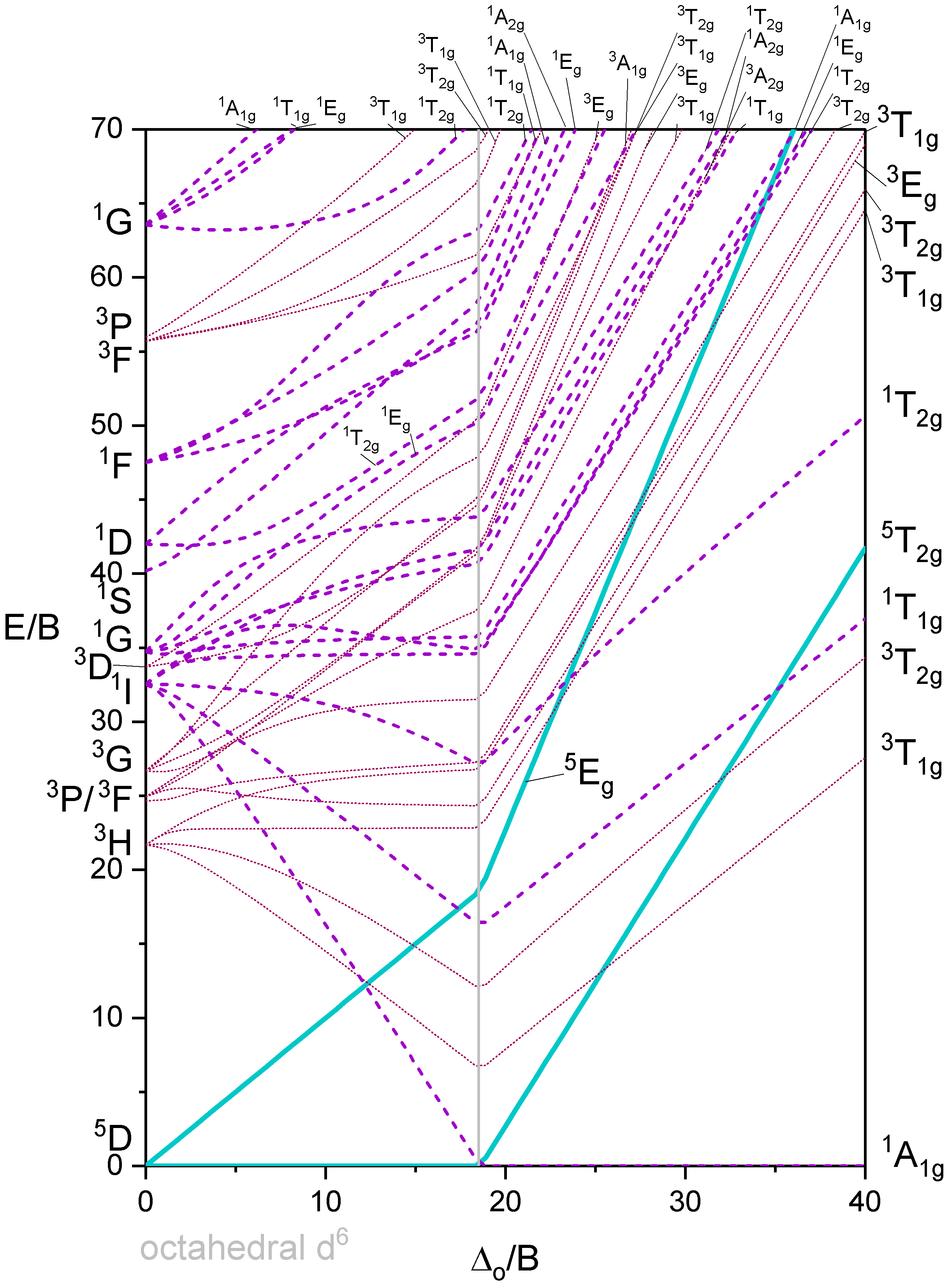
Octaedro con 7 electrones d

Figura\(\PageIndex{8}\):\(d^7\): Diagrama Tanabe-Sugano para el complejo metálico octaédrico con siete\(d\) electrones. Una línea vertical gris a 21.7\(\frac{\Delta_o}{B}\) divide los casos de alto giro de los casos de giro bajo. Para mayor comodidad, los términos que pueden acomodar transiciones permitidas por giro desde el estado fundamental del cuarteto en giro alto (izquierda de la línea gris) se indican mediante líneas sólidas pesadas. Los términos que pueden acomodar transiciones permitidas por giro desde el estado fundamental del doblete de giro bajo se muestran en líneas discontinuas pesadas. (CC-BY-SA; Kathryn Haas)

Octaedro con 8 electrones d

Figura\(\PageIndex{9}\):\(d^8\): Diagrama Tanabe-Sugano para el complejo metálico octaédrico con ocho\(d\) electrones. Para mayor comodidad, los términos que pueden acomodar transiciones permitidas por giro desde el estado fundamental se indican mediante líneas continuas. Los términos que tienen multiplicidad diferente al estado fundamental se muestran en líneas discontinuas. (CC-BY-SA; Kathryn Haas)