1.4: Habilidades cuantitativas

Última actualización
Guardar como PDF

Page ID: 56375

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Variables

La ciencia experimental analiza los tipos de relaciones de causa y efecto. Los experimentos controlados varían uno de los factores o rasgos para observar el efecto sobre otro factor o rasgo. Estos factores se denominan variables. Una variable dependiente es algo que se observa y se espera que cambie como resultado de modificar otro factor en el experimento. Es decir, el resultado depende de otro factor. Otro nombre para la variable dependiente es la variable de respuesta. La variable independiente es el factor o condición que está cambiando o siendo cambiado por el experimentador. A veces esperar es la condición que está cambiando, haciendo la variable independiente: el tiempo. Dado que cambiamos la variable independiente, también se llama la variable manipulada.

Graficando una Línea

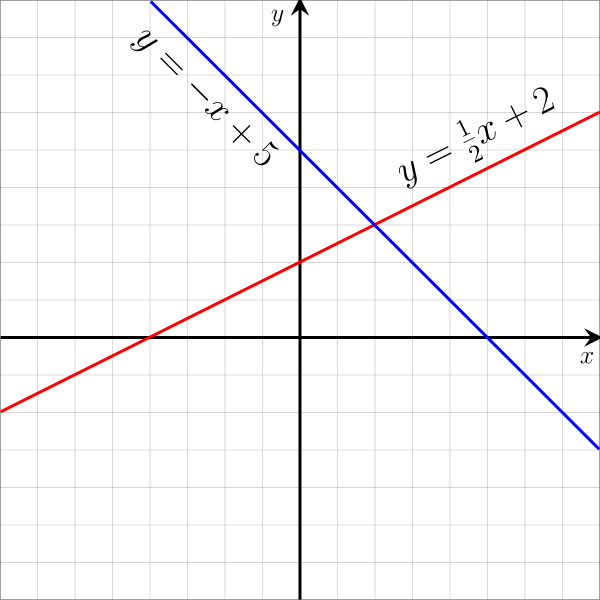
Un gráfico que muestra 2 líneas y sus ecuaciones

Una línea puede ser descrita matemáticamente por la ecuación:

Esto se conoce como la forma pendiente-intercepción. Las 2 variables y y x se refieren a coordenadas a lo largo de cada eje. El término m se refiere al cambio en los valores y sobre el cambio en los valores x. Esto se conoce como la pendiente de la línea. El término b, la intercepción y, es el valor y donde la línea cruza el eje y.

$m =\ frac {y_2-y_1} {x_2-x_1}$ O $m =\ frac {\ Delta y} {\ Delta x}$

Es así como se determina la pendiente de una línea (m).

La pendiente de la línea indica la relación entre las dos variables, x e y, La ecuación de la línea nos indica que “y” ocurre en función de los cambios a “x”. A veces esto está representado por la ecuación. Dado que “y” depende de “x”, “y” es la variable dependiente y “x” es la variable independiente. A medida que cambia “x”, ¿cómo cambia “y” en respuesta? Esto es lo que nos revela la pendiente.

Para más revisión, visite el siguiente enlace.

Actividad de taludes

Graficar líneas

Haga clic aquí para ejecutar la simulación.

Actividad de trazado de datos

Utilice los siguientes datos del USDA para trazar una gráfica de dispersión y generar una línea de tendencia.
Use la información de la tabla a continuación o descargue (un archivo de texto que se puede abrir en notepad/textedit)
Siga un tutorial sobre cómo graficar una gráfica de dispersión con línea de mejor ajuste (línea de tendencia)
O usa este tutorial en plot.ly
- Mostrar la ecuación de la línea de tendencia en la gráfica
- Asegurar que “lbs. mozzarella” es el eje y
- Asegurar que “Año” es el eje x
- Recuerda no usar un gráfico de líneas

Año	lbs. mozzarella
2000	9.33
2001	9.70
2002	9.66
2003	9.65
2004	9.94
2005	10.19
2006	10.52
2007	11.02
2008	10.57
2009	10.63

¿Qué Aprendemos?

¿Qué nos dice este diagrama de dispersión sobre la relación entre el consumo de mozzarella en relación con los años?
¿Cómo influiría esta gráfica en la forma en que inviertes en una empresa de queso mozzarella? ¿Se puede predecir algo sobre el futuro del consumo de queso?
¿Qué te indica la pendiente de esta línea?
1. Usa las matemáticas para ilustrar este punto.
2. La pendiente tiene una unidad relacionada con “lbs.” y “año”, ¿qué es esta unidad?

Creando una Línea de Mejor Ajuste

No todos los puntos recogidos caerán en línea recta. Una Línea de Mejor Ajuste o una Línea de Tendencia aproxima el promedio de esos puntos a través de un proceso matemático llamado método de mínimos cuadrados. Mientras que uno podría “globo ocular” esta línea, el método de mínimos cuadrados utiliza los datos para minimizar la distancia desde todos esos puntos a la línea para tener un efecto promediador.

Crear una columna de datos para valores “x”, valores “y”, x ² y xy
En la parte inferior de estas columnas, suma los datos. σx, σy, σx ², σxy
Calcular la pendiente a partir de estos valores
- $m =\ frac {N (\ Sigma xy) -\ Sigma x\ Sigma y} {N (\ Sigma x^2) - (\ Sigma x) ^2}$ (donde N = número de entradas en una columna)
Calcular la intercepción y a partir de estos valores
- $b =\ frac {N (\ Sigma y) - m (\ Sigma x)} {N}$
Que proporciona el uso de la función

Regresión por mínimos cuadrados

Haga clic aquí para ejecutar la simulación.

Search

Text Color

Text Size

Margin Size

Font Type

¿Qué Aprendemos?