2.5: pH

Última actualización
Guardar como PDF

Page ID: 56410

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

pH

Ácidos y Bases

Podemos llamar ácido a cualquier compuesto que agregue iones H ⁺ (un protón libre) en solución. Junto con esto, esperaríamos que cualquier compuesto que disminuyera la concentración de H ⁺ libre de una solución como base. El pH es el poder de H ⁺ de una solución. Definimos este poder como una concentración molar de H ⁺ en solución. Esta concentración invariablemente termina siendo un número relativamente pequeño (aunque grande en números absolutos) y se expresa como un número decimal. Debido a que el rango de las concentraciones es tan grande, expresamos estos números como números logarítmicos para evitar escribir muchos 0's después del decimal y para facilitar la comunicación de la concentración. Dado que estos números son tan (relativamente) pequeños, utilizamos el logaritmo negativo para describir esta concentración.

Definido matemáticamente, $pH=-\ log_ {10}\ lbrack {H} ^+\ rbrack$

La escala de pH oscila para que cualquier cosa por debajo de pH 7 sea ácida y cualquier cosa por encima de pH 7 sea alcalina. Entonces un número menor es más ácido. Pero, ¿no acabamos de afirmar que algo ácido contiene más iones H ⁺? Recuerden, porque estamos tratando con un Logaritmo negativo, esto quiere decir que la concentración es mayor.

Escalas logarítmicas

Si tenemos una cantidad que es 10 ², sabemos que se traduce en 100. Así como si tuviéramos una cantidad de 10 ⁴, sabemos que eso se traduce en 10000. Así como se vuelve inconveniente seguir escribiendo todos esos 0, es realmente poco práctico escribir muchos 0 después de un decimal. ¡También es muy difícil hablar de eso! Por lo que de igual manera expresaremos números como 0.0001 como 10 ^-4. Un logaritmo es la función inversa de un exponente. Por lo tanto:

$\ log_ {10} ({0.0001}) =-4$
$\ log_ {10} ({10} ^ {-4}) =-4$

Entonces, ¿cómo definimos una solución que es pH 2? Bueno, ya decidimos que esta solución está por debajo de pH 7 —convirtiéndola en un ácido. Pero, ¿qué significa esto en términos de concentración de iones H ⁺?
Vamos a resolver esto algebraicamente:

$pH=-\ log_ {10}\ lbrack {H} ^+\ rbrack$ Vamos a llevar el (-) al otro lado
$-pH=\ log_ {10}\ lbrack {H} ^+\ rbrack$ Ahora vamos a revertir el Log → base 10
$10^ {-pH} =\ lbrack {H} ^+\ rbrack$ Enchufe el pH → concentración molar de [H ⁺]

Como podemos ver ahora, una solución de pH 2 es ácida porque la concentración molar de [H ⁺] es de 10 ^-2 moles/L o 0.01M

Disociación de iones: ¡Ese número es pequeño!

No es un número pequeño. Recuerda que un mole es 6.022 X 10 ²³. ¡Ese es un número muy grande! ¡Piénsalo! Una solución de pH 4 es ácida, pero si enchufamos la fórmula, nos damos cuenta de que esto es igual a 0.0001M H ⁺ — ¡menor que pH 2 a 0.01M!

Pero comparémoslo con el contenido [H ⁺] de H ₂ O. ¡Ahora voy a sonar más loco! Se puede pensar que el agua está en un equilibrio donde algunas de las moléculas son ionizantes y desionizantes. Podemos expresarlo de 2 maneras:

H ₂ O H ⁺ + OH ^—
2H ₂ O H ₃ O ⁺ OH ^—

Por lo que en cualquier punto dado, un litro de H ₂ O a pH neutro (7) tiene 10 ^-7 moles de iones H ⁺. Por cierto, también tiene 10 ^-7 moles de OH ^— en solución. La segunda expresión indica la formación de un ion hidronio (H ₃ O ⁺) en lugar de un protón libre en solución. Entonces algo que es pH 2 es un ácido más fuerte que pH 4, ¿verdad? No. Eso solo indica la cantidad de protones libres en solución. Es más ácida pero la fuerza ácida significa otra cosa. Cuando hablamos de ácidos fuertes, significa que es más probable que se done un protón a la solución porque es más probable que se ionice. Veamos lo siguiente:

HA H ⁺ (aq) + A ^— (aq) Donde HA es un ácido que se disocia en solución

Si esta disociación es muy alta, entonces decimos que es un ácido fuerte. ^{De manera similar, un compuesto como el NaOH se disocia fácilmente por completo en solución y proporciona OH, iones que pueden eliminar fácilmente H ⁺ de la solución, ¡una base fuerte!} Hablamos de disociación en términos de tasas y lo expresamos como la constante de disociación ácida, K _a. Esto se calcula utilizando las concentraciones de [H ⁺] (protón), [A ^—] (base conjugada) y [HA] (no disociada) en equilibrio:

$K_ {a} =\ frac {[{H} ^+] [{A} ^-]} {[{HA}]}$

Al igual que los órdenes de magnitud que tenemos al discutir el pH, las tasas de disociación se comunican más convenientemente en una escala logarítmica.

${p} K_ {a} = -\ log_ {10} {K_ {a}}$

Piénsalo de esta manera, si la concentración de los iones disociados es muy alta, el numerador en la tasa es muy alto → K _a es grande. En otras palabras, en equilibrio, la reacción de disociación parece más unidireccional que bidireccional ya que el compuesto se ioniza fácilmente:

HA → H ⁺ (aq) + A ^— (aq)

En esta escala, nos referimos a cualquier cosa con _un pK a < -2 como un ácido fuerte ya que se disociará fácilmente en solución. Esta forma de la constante de disociación es extremadamente útil para estimar el pH de las soluciones tamponadas y para encontrar el pH de equilibrio de la reacción ácido-base (entre el protón y la base conjugada). Podemos estimar el pH utilizando la ecuación de Henderson-Hasselbalch:

${pH} = {p} K_ {a} +\ log_ {10}\ izquierda (\ frac {[{A} ^-]} {[{HA}]}\ derecha)$

Soluciones Bufferadas

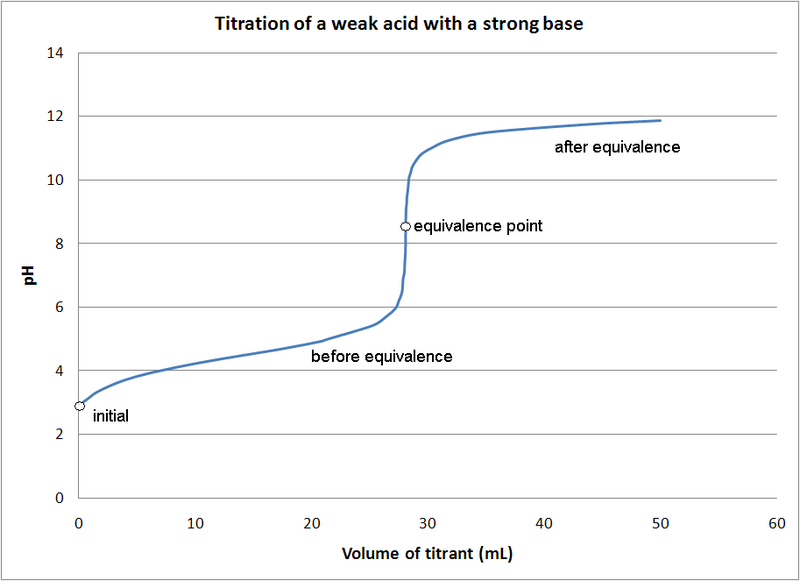
Un búfer es algo que resiste el cambio. Una solución tamponada es aquella que consiste en un ácido débil o una base débil que controlará el pH de una solución. Imagine que un tampón es un depósito de iones H+ u OH- disponibles. Si una solución tamponada tiene pH 2, agregarle una solución básica no provocará un cambio drástico en el pH porque el reservorio de H+ neutralizará continuamente la base. Eventualmente, esta tienda o reservorio de H+ se agotará. Cuando esto suceda, el pH cambiará repentinamente. El rango en el que se agrega ácido o base sin un cambio significativo en el pH se denomina zona tamponada o capacidad tamponadora. Cuando se agota esta reserva de H+ o capacidad de tamponamiento, hemos alcanzado el punto de equivalencia que describe el punto en el que la base ha neutralizado completamente el ácido débil.

Titulación de un ácido por una base La solución tiene una buena capacidad de tamponamiento entre pH 3 y pH 5

Simulación de ácidos y bases

Haga clic aquí para ejecutar la simulación sobre Ácidos y Bases

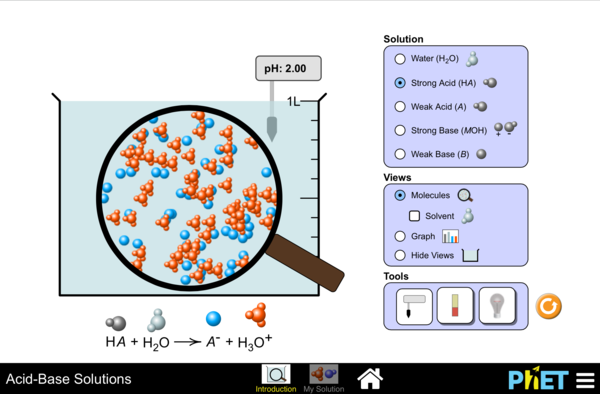
Simulación de pH

Escala de pH

Haga clic aquí para ejecutar la simulación en escalas de pH

Usa la siguiente tabla para indicar si un ítem es un ácido o una base y cuál predices que será el pH. Podemos determinarlos en clase a través de la medición.

Solución	Ácido o Base	pH pronosticado	pH real
Café
Cola
Destilado H ₂ O
Detergente
Bleach
Zumo de Manzana
Solución antiácida

Search

Text Color

Text Size

Margin Size

Font Type