16.6: Análisis Morfomético

Última actualización
Guardar como PDF

Page ID: 56332

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Morfometría y Marcadores Físicos

Morfometría (morfo — forma; métricas — mediciones) es el uso de mediciones físicas para determinar la relación de organismos. Con organismos extintos que se extinguieron hace mucho tiempo, la extracción de ADN resulta difícil. Asimismo, antes de las tecnologías de ADN para analizar especies, la taxonomía linneana se atribuyó a organismos en base a similitudes en características.

Describiendo especies y variación de morfologías

A continuación se muestran imágenes de hitos de cráneo de la familia de lagartos Varanidae. Esta familia incluye lagartos monitor y Dragones de Komodo. Como se puede ver a continuación, la morfología general de los cráneos es lo suficientemente similar como para que todos conserven los mismos hitos. La siguiente figura también ilustra la diversidad en estas lagartijas que ilustran una gran variación entre especies.

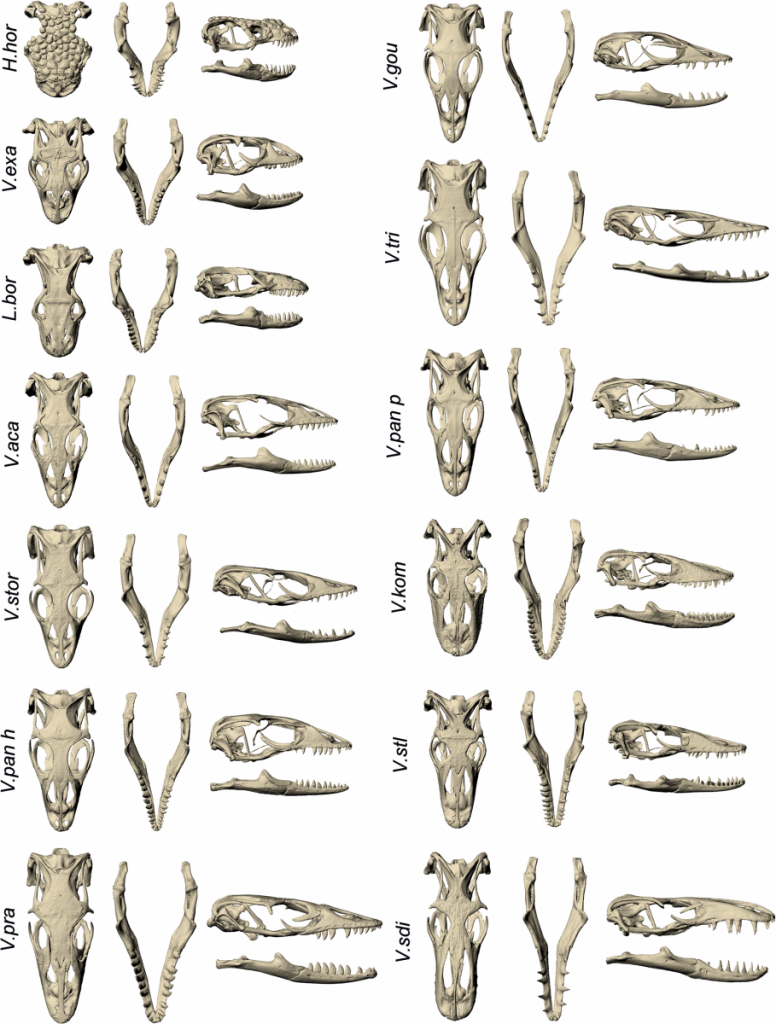
periodal.pone_.0130625.g005-776x1024.png

Calaveras de las especies involucradas en este análisis. McCurry y otros (2015) (CC-BY)

Hitos Estandarizar mediciones

Tener un conjunto de puntos de referencia compartidos brinda la oportunidad de realizar mediciones sistemáticas de características morfométricas.

periodal.pone_.0130625.g002-1024x829.png

Hitos y métricas de medición para el análisis morfométrico de cráneos. McCurry y otros (2015) (CC-BY)

Distancia euclidiana para medir la relación

La distancia euclidiana es una medida derivada de la geometría pitagórica que describe la distancia más corta ($d$) entre 2 puntos ($A$y$B$) como una línea recta usando triangulación. En un espacio cartesiano, los puntos se pueden definir:

\[A = \left( x _ { A } , y _ { A } \right)\nonumber \]

\[B = \left( x _ { B } , y _ { B } \right)\nonumber \]

El teorema estándar de Pitágoras se puede expresar como:

\[x ^ { 2 } + y ^ { 2 } = d ^ { 2 }\nonumber \]

Para encontrar la distancia entre los 2 puntos, utilizamos álgebra para calcular.

\[d = \sqrt { x ^ { 2 } + y ^ { 2 } }\nonumber \]

En este caso, ampliamos para comparar las coordenadas de los dos puntos:

\[\Delta x = x _ { B } - x _ { A }\nonumber \]

\[\Delta y = y _ { B } - y _ { A }\nonumber \]

Luego podemos ampliar esta idea para incluir las diferencias en los puntos de datos que describen las comparaciones de múltiples mediciones.

\[d \left( \mathbf { X } _ { \mathbf { i } } , \mathbf { X } _ { \mathbf { j } } \right) = \sqrt { \sum _ { k = 1 } ^ { p } \left( X _ { i k } - X _ { j k } \right) ^ { 2 } }\nonumber \]

Cálculo de distancia con R

Descargar el conjunto de datos (McCurry et al. 2015) asociados a esta actividad (un archivo.csv de Valor Separado por Comas). Esto se puede utilizar en una hoja de cálculo o en un editor de texto. Estos datos se pueden importar a R para determinar las distancias euclidianas de los hitos.
El siguiente código en R descargará el conjunto de datos en una variable llamada “varanoid”, medirá la distancia euclidiana y guardará una gráfica en un archivo PDF en un directorio llamado “/tmp”.

## instalar curl para buscar de internet si no lo es

install.packages ('curl')

## Cargar la biblioteca curl

biblioteca (curl)

## leer los datos de las mediciones y asignarlos a una variable 'varanoide'

varanoid = read.csv (curl ('https://raw.githubusercontent.com/jeremyseto/bio-oer/master/data/varanoid.csv'))

## establecer los nombres de fila en la columna Especie

fila.nombres (varanoid) = varanoid$especies

## eliminar la primera columna de la tabla para tener datos puramente numéricos

varanoid_truncado = (varanoid [, 2:14])

## calcular la distancia usando euclidiano como método

dist_measure = dist (varanoid_truncado, método= 'euclidiano')

## mostrar dist_measure para ver las comparaciones

dist_measure

varanoid_cluster = hclust (dist_measure)

## abrir PDF como dispositivo gráfico para guardar un archivo en el directorio '/tmp'

pdf (archivo= '/tmp/varanoid_tree.pdf')

plot (varanoid_cluster)

dev.off ()

## cierra el dispositivo para guardar la trama como pdf

Análisis de ADN

Antes de iniciar esta actividad, revisar la bioinformática y el análisis de secuencias.

Buscar en NCBI secuencias mitocondriales de las especies involucradas en McCurry 2015. Los datos han sido presentados por Ast (2001).
Encontrar las secuencias e identificar/extraer elementos que son comunes a todos.
Ensamble las secuencias compartidas en un editor de texto como un solo archivo FASTA donde cada especie está separada por un encabezado (“>Especie A”).
- Bloc de notas en Windows (pero es mejor descargar notepad++)
- Textedit en Mac (pero probablemente mejor para descargar TextWrangler)
- Gedit en Linux
Guardar el archivo como “algo.fasta”.
Realizar un análisis de múltiples secuencias usando UGENE.
Generar un árbol filogenético usando UGENE. Para este ejercicio, use Máxima Verosimilitud (PhyML) como algoritmo. Presenta el tutorial a continuación.
Comparar el ADN con los análisis morfométricos. ¿Qué problemas podríamos imaginar que surjan si dependemos únicamente de la morfometría?

Referencias

McCurry MR, Mahony M, Clausen PD, Quayle MR, Walmsley CW, Jessop TS , Woe S, Richards H, McHenry CR. (2015) La relación entre la estructura craneal, Desempeño Biomecánico y Diversidad Ecológica en Lagartos Varanoides. PLoS ONE 10 (6): e0130625. doi: 10.1371/periodista.pone.0130625
Ast, Jennifer C. (2001) Evidencia y evolución del ADN mitocondrial en Varanoidea (Squamata). Cladística 17 (3): 211—26. http://www.sciencedirect.com/science/article/pii/S0748300701901690
Fisher, R.A. (1936) El uso de múltiples mediciones en problemas taxonómicos. Anales de Eugenesia, 7:179—188. doi:10.1111/j.1469-1809.1936.tb02137.x

Search

Text Color

Text Size

Margin Size

Font Type