17.1: Introducción al Capítulo
( \newcommand{\kernel}{\mathrm{null}\,}\)
En la Ecuación 8.1, el mutualismo ocurre cuando los términos de interacción,s1,2 ys2,1, son ambos positivos. Esta es la característica definitoria del mutualismo. Los términos de autocompromiso,s1,1 ys2,2, pueden ser positivos o negativos, y los términos de crecimiento intrínseco,r1 yr2, también pueden ser positivos o negativos.
Si ambos términos de crecimientori son positivos, entonces cualquiera de las especies puede sobrevivir por sí sola, sin la presencia de la otra. Esto se llama “mutualismo facultativo”. Un ejemplo es el mutualismo entre el pájaro buey y el brujo de guerra (Figura 9.2 a la izquierda). Los pájaros bueyes tienen otras fuentes de alimento, y los warthogs pueden sufrir pero probablemente no mueren a causa de mayores cargas de parásitos.
Si ambosri son negativos, entonces ninguna de las especies puede sobrevivir por sí sola sin la presencia de la otra. Esto se llama “mutualismo obligado”. Un ejemplo es el liquen, compuesto por una alga y un hongo. Si el hongo solo se coloca sobre una roca, morirá. Aunque puede comer roca, o, más exactamente, puede disolver los nutrientes de la roca, no puede producir compuestos de carbono a partir de la roca. Y si las algas por sí solas se colocan sobre una roca, morirán. Aunque puede producir compuestos de carbono a partir del aire a través de la fotosíntesis, no puede comer roca. Pero los dos juntos se convierten en una asociación perfecta, cada uno cubriendo las debilidades del otro.
Figura17.1.1. La fotosíntesis es la base de muchos mutualismos. Euglena es una combinación protista y cloroplasto que puede fijar el dióxido de carbono del agua, cambiar la naturaleza del protista y puede moverse distancias siguiendo los nutrientes, apoyando al cloroplasto. Los cloroplastos parecen ser cianobacterias muy modificadas, que se vuelven totalmente dependientes de sus parejas por eones de evolución (izquierda, a través de un microscopio). Los líquenes son combinaciones de hongos y algas en las que el componente algal puede fijar carbono y el componente fúngico puede disolver los nutrientes de la roca (media, altura del hombro). Los corales son antozoos, animales marinos con tentáculos picantes para capturar alimentos, que a menudo construyen arrecifes y se asocian con algas marinas. Una fracción significativa del carbono del mundo es secuestrado en los arrecifes de coral (derecha, desde el espacio).
Cuandor1 es positivo yr2 es negativo, o viceversa, es un mutualismo parcialmente obligado. Una especie depende de una segunda, pero la segunda puede llevarse bien sin la primera. Esta es una posibilidad matemática, y algunos casos como el cloroplasto— euglena pueden ser ejemplos (Figura17.1.1 izquierda), donde el cloroplasto no puede vivir sin el protista, pero el protista sí.
Además del mutualismo obligado versus facultativo, existe otra distinción importante. Esto es entre el mutualismo “moderado” y el “desenfrenado”. Esta distinción no suele hacerse en los libros de texto porque está relacionada con la diferencia entre el crecimiento poblacional logístico y ortólogo, que normalmente no está cubierto.
Cuando los efectos autolimitantes de los términoss1,1 ys2,2 son más fuertes que los términos de mejora entre especiess1,2 ys2,1, el par mutualista tiene una capacidad de carga que se puede calcular a partir de las propiedades de las especies individuales. Alcanzan su capacidad de carga conjunta a lo largo de un camino que parece crecimiento logístico, y es idéntico en forma a la de dos especies competidoras que coexisten y alcanzan una capacidad de carga conjunta. Sin embargo, cuando los efectos autolimitantes des1,1 ys2,2 son más débiles que los términos de mejora entre especiess1,2 ys2,1, la capacidad de carga del par de especies no se puede calcular a partir del valor de esos parámetros, y aumentan cada vez más rápidamente hasta que algún otro limitación es golpeada.
Piensa de nuevo en el liquen. La capacidad de carga de cada especie es esencialmente cero cuando viven por separado en la superficie de una roca. Juntos, sin embargo, pueden cubrir la roca, y su capacidad de carga conjunta en la Tierra está relacionada con el área total de rocas en la Tierra, además de otros hábitats adecuados como la corteza de los árboles, la superficie exterior de un automóvil desguazado y descuidado durante décadas, y una miríada de otras superficies de otra manera inhabitables. El área de rocas en el mundo, y otras superficies adecuadas, ciertamente no es parte de los parámetros r i y s i, j! Esto es bastante diferente a la situación de competencia y depredación, en la que la capacidad de carga conjunta está codificada en los parámetros. Por qué esto debería ser es revelado por algunos diagramas y las matemáticas correspondientes.
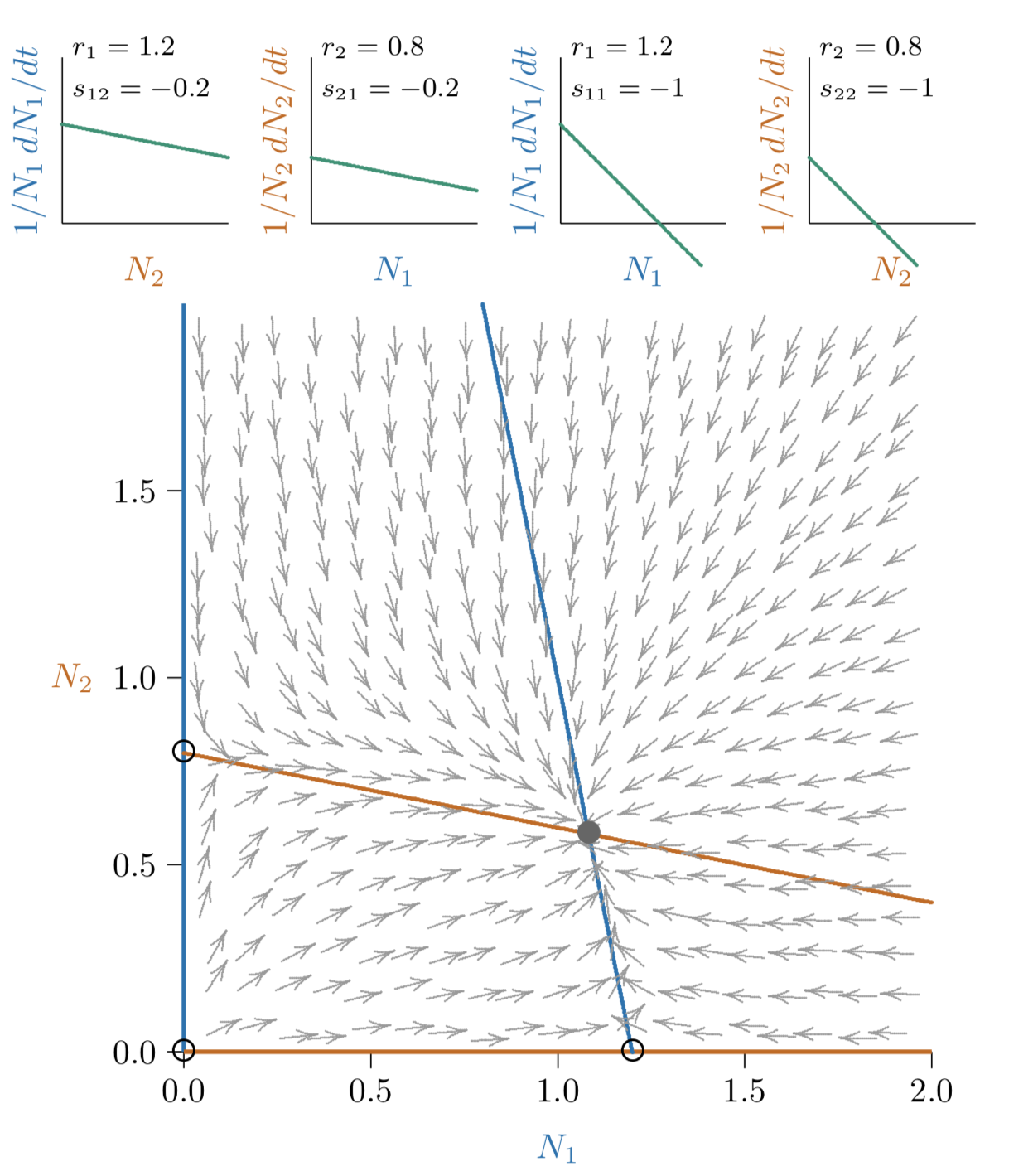
Figura17.1.2. El espacio de fase para la competencia es más débil que el de la Figura 10.11. El equilibrio articular (círculo relleno de negro) está más cerca a lo largo de los ejes a las capacidades de carga individuales (círculos abiertos).
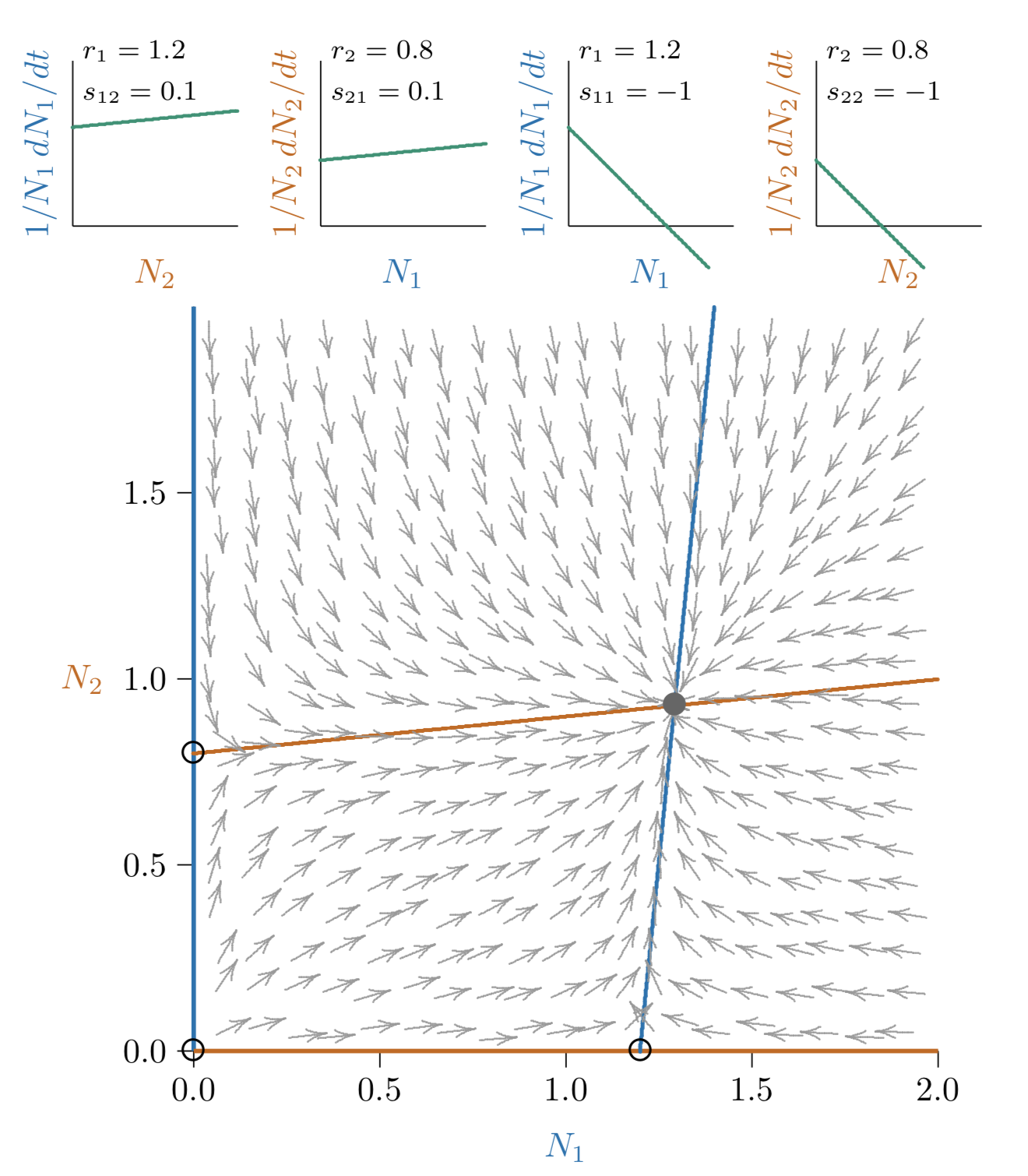
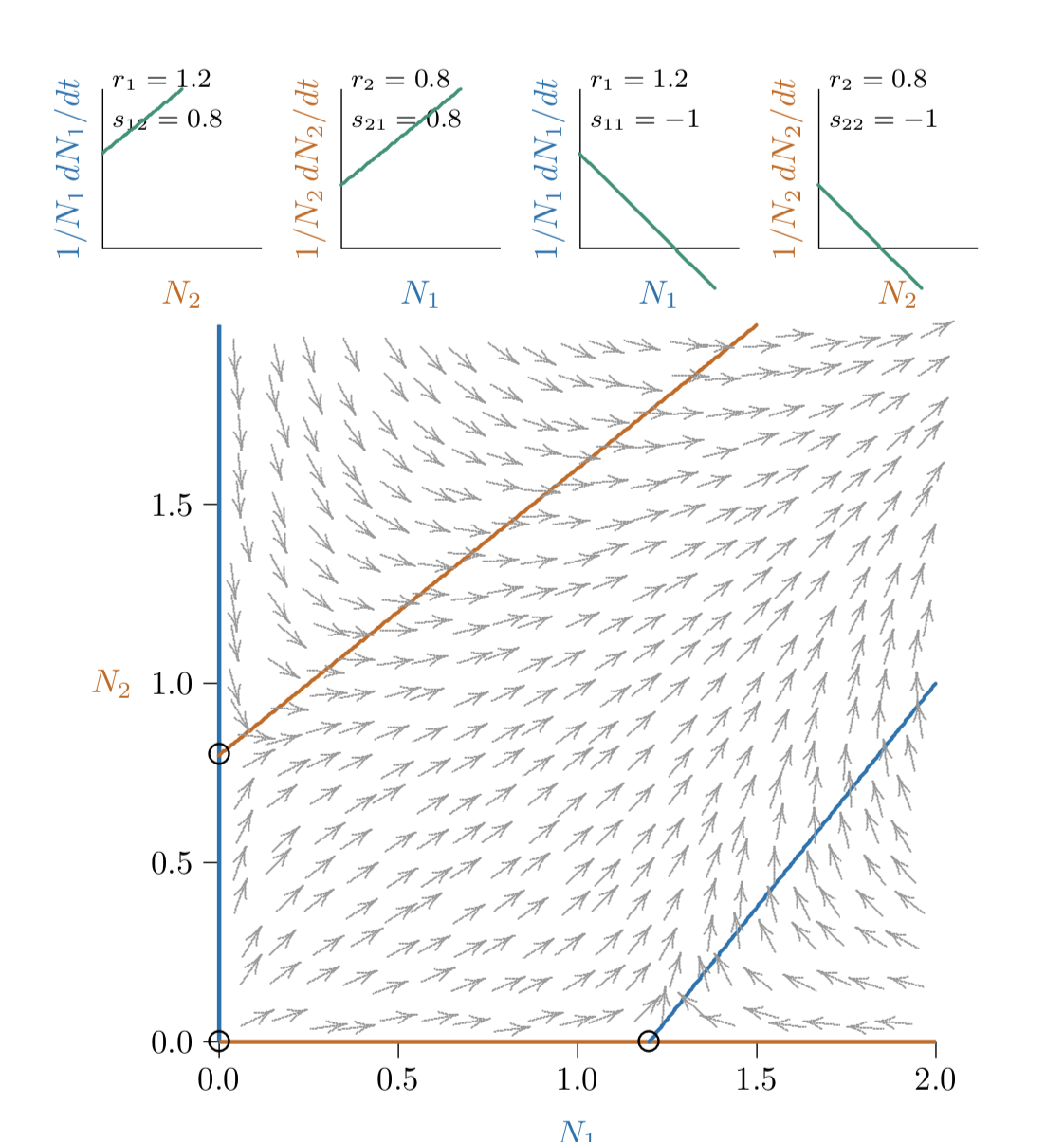
Figura Espacio de17.1.4 fase para un mutualismo más fuerte, pero aún limitado, porque todavía existe un equilibrio conjunto (aunque lejos de la gráfica en la intersección de las isoclinas roja y azul).
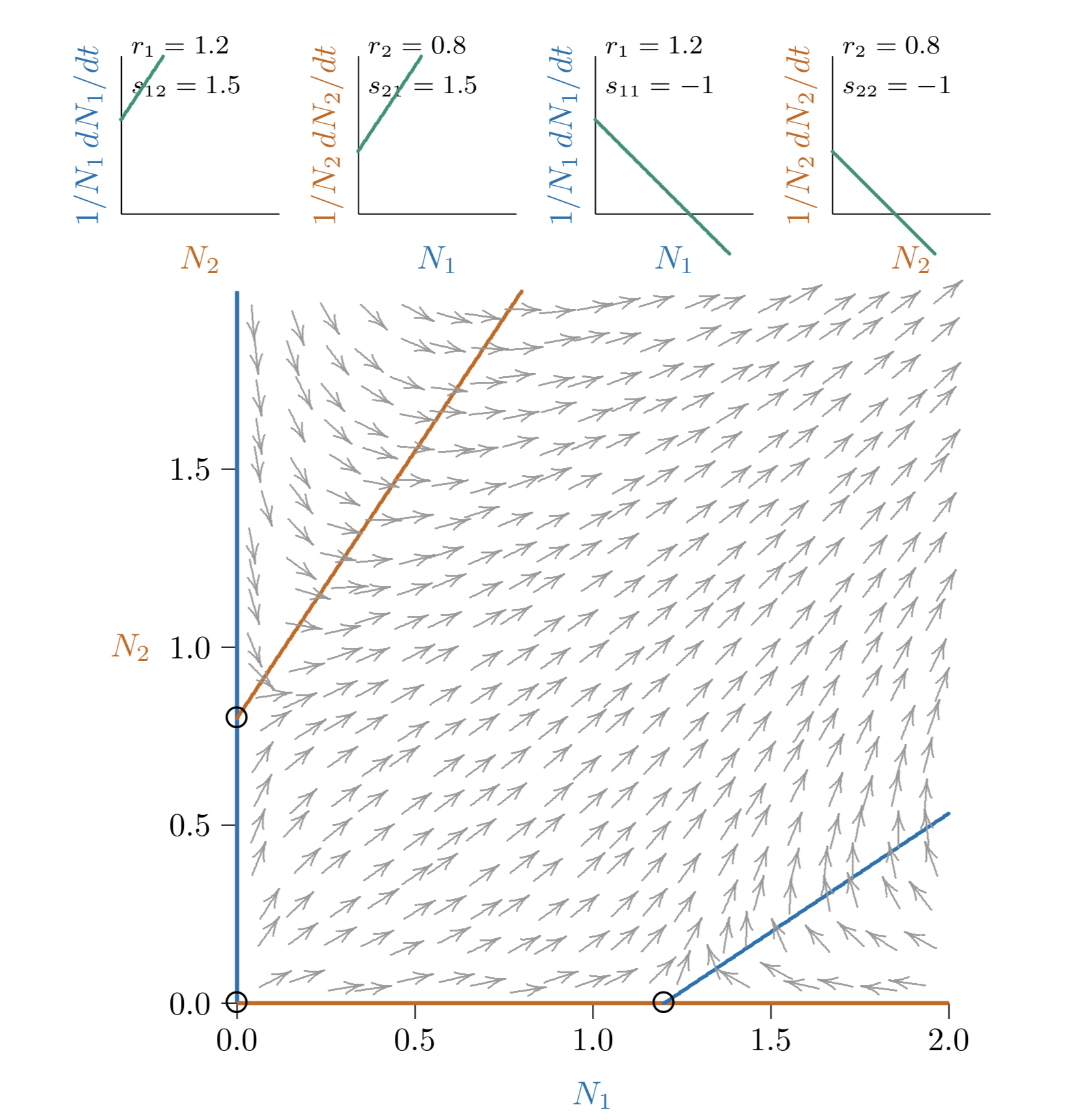
Figura17.1.5. Con un mutualismo ligeramente más fuerte todavía, el equilibrio conjunto desaparece —no se puede determinar a partir de los parámetros— y la relación mutualista se vuelve “desenfrenada”.
Figura17.1.6. A medida que las especies mutualistas se vuelven más dependientes unas de otras, sus capacidades de carga individuales se vuelven más pequeñas (los círculos abiertos aquí están más cerca del origen).


