6.1 Racionalidad
Una suposición conductual crítica en la economía es que los agentes operan de una
manera orientada hacia el logro de una meta. Esto puede interpretarse en el
sentido de que individuos y empresas maximizan su bienestar personal y/o
sus ganancias. Estos jugadores pueden tener otros objetivos además: La filantropía
y el bienestar de los demás son consistentes con la optimización individual.
Si los individuos van a lograr sus metas entonces deben actuar de una manera
que los lleve a su objetivo; en términos generales, deben actuar de
manera racional. La teoría de la maximización individual que desarrollaremos en este
capítulo se basa en esa premisa o suposición. Al asumir que los individuos son
racionales no necesitamos asumir que tienen toda la información
disponible para ellos que pueda ser relevante para una decisión o elección específica.
Tampoco es necesario asumir que tienen súper computadoras en su cerebro cuando
evalúan posibles estrategias alternativas.
Lo que sí hay que asumir, sin embargo, es que los individuos actúan de una manera consistente con la obtención de un objetivo determinado.
La teoría moderna de la economía del
comportamiento y la psicología conductual examina la toma de decisiones en
una amplia gama de circunstancias y ha descubierto muchos comportamientos
fascinantes, algunos de los cuales se desarrollan en el Recuadro de Aplicación 6.1
a continuación.
En el Capítulo 1 indicamos que, como científicos sociales,
requerimos un modelo confiable de comportamiento, es decir, una manera de
describir los elementos esenciales de la elección que sea consistente con
las observaciones cotidianas sobre los patrones de comportamiento individuales. En este capítulo, nuestro objetivo es comprender más
a fondo las fuerzas conductuales que impulsan el lado
de la demanda de la economía.
Los economistas analizan la toma de decisiones individuales utilizando dos enfoques diferentes, pero
complementarios: el análisis de utilidad y el análisis de indiferencia.
Comenzamos retratando a los individuos como maximizando su
utilidad medible (a veces llamada utilidad cardinal); luego avanzamos hacia el análisis de
indiferencia, donde se hace una suposición más débil sobre la capacidad de los
individuos para medir su satisfacción. En esta segunda instancia no
asumimos que los individuos puedan medir su utilidad numéricamente, sólo que
puedan decir si una colección de bienes y servicios les produce mayor
satisfacción que otro grupo. Este ranking de opciones corresponde a lo que a veces
se llama utilidad ordinal — porque los individuos pueden
ordenar grupos de bienes y servicios en orden ascendente de
satisfacción. En cada caso los individuos son percibidos como maximizadores racionales
u optimizadores: Destacan sus ingresos para elegir el resultado que los
hará lo más acomodados posible.
El segundo enfoque del comportamiento del consumidor se omite frecuentemente en los textos
introductorios. Aquí se puede omitir sin interpretar el flujo de
ideas, aunque sí arroja conocimientos adicionales sobre la elección del consumidor y la política
gubernamental. Al igual que en los capítulos anteriores, comenzamos el análisis con
un ejemplo numérico motivador.
Aplicación Box 6.1 Racionalidad e impulso
Recientemente han aparecido varios libros informativos y populares sobre la toma de decisiones. Su tema central es que nuestros procesos de decisión no deben ser vistos únicamente como una computadora racional, operando en un solo modo, e impasible de nuestras emociones o historia. Los psicólogos ahora saben que nuestros cerebros tienen al menos dos modos de decisión, y estos son desarrollados por el ganador del Premio Nobel de economía Daniel Kahneman en su libro “Pensando, rápido y lento”. Una parte de nuestro cerebro opera de una manera racional orientada a objetivos hacia el futuro (la parte 'lenta'), otra está motivada por la gratificación inmediata (la parte 'rápida'). Las decisiones que observamos en el mundo sobre nosotros reflejan estos diferentes mecanismos.
Richard Thaler, economista de Chicago y su colega profesor de derecho Cass Sunstein, han desarrollado un papel para las políticas públicas en su libro titulado “Nudge”. Ellos también argumentan que los individuos no operan inevitablemente en sus propios intereses a largo plazo y, como consecuencia, los individuos frecuentemente requieren un empujón del gobierno para tomar la decisión a largo plazo en lugar de la elección a corto plazo. Por ejemplo, cuando los individuos inician un nuevo empleo, se les puede inscribir automáticamente en el plan de pensiones de la empresa y se les da la libertad de optar por no participar, en lugar de no estar inscritos y darles la opción de optar por participar. Dichas políticas se consideran 'paternalismo suave'. Son paternalistas por la razón obvia —otro organismo está dirigiendo, pero también son suaves porque no son vinculantes.
6.2 Elección con utilidad medible
A Neal le encanta abrirse paso a través del polvo de gran altitud en la estación de
esquí y snowboard de Whistler. Su costo de boleto elevador con tarifa de estudiante es de $30 por
visita. También le encanta frecuentar los bares de jazz en el centro de Vancouver, y
cada visita de este tipo le cuesta 20 dólares. Con pasiones caras, Neal debe destinar cuidadosamente
su presupuesto mensual de entretenimiento. Ha evaluado cuánta
satisfacción, medida en utils, obtiene de cada salida de snowboard y
cada visita al club de jazz. Suponemos que estas utils son medibles, y utilizamos el
término utilidad cardinal para denotar esto. Estos
valores de utilidad medibles se enumeran en las columnas 2 y 3 del Cuadro 6.1.
Definen la utilidad total que obtiene de diversas cantidades de las
dos actividades.
Tabla 6.1 Utils del snowboard y el jazz
|
1 | 2 | 3 | 4 | 5 | 6 | 7 |
|
Visita | Total | Total | Marginal | Marginal | Marginal | Marginal |
|
# | snowboard | jazz | snowboard | utils de jazz | snowboard | utils de jazz |
|
| utils | utils | utils | | utils por $ | por $ |
|
1 | 72 | 52 | 72 | 52 | 2.4 | 2.6 |
|
2 | 132 | 94 | 60 | 42 | 2.0 | 2.1 |
|
3 | 182 | 128 | 50 | 34 | 1.67 | 1.7 |
|
4 | 224 | 156 | 42 | 28 | 1.4 | 1.4 |
|
5 | 260 | 180 | 36 | 24 | 1.2 | 1.2 |
|
6 | 292 | 201 | 32 | 21 | 1.07 | 1.05 |
|
7 | 321 | 220 | 29 | 19 | 0.97 | 0.95 |
Precio de la visita de snowboard = $30. Precio de la visita al club de jazz = $20.
La utilidad cardinal es un concepto medible de satisfacción.
La utilidad total es una medida de la satisfacción total derivada del consumo de una determinada cantidad de bienes y servicios.
La utilidad total de Neal para cada actividad en este ejemplo es independiente de
la cantidad de la otra actividad en la que realiza. Estas utilidades totales se
representan en las Figuras 6.1 y 6.2.
Claramente, más de cada actividad produce más utilidad, por lo que la utilidad adicional o
marginal (MU) de cada actividad es positiva. Esta utilidad marginal
positiva para cualquier cantidad del bien consumido, por
mucho que sea, refleja el supuesto de no saciación —más siempre es
mejor. Tenga en cuenta, sin embargo, que las pendientes decrecientes de las
curvas de utilidad total muestran que la utilidad total está aumentando a una tasa decreciente.
Si bien más es ciertamente mejor, cada visita adicional a Whistler o a un
club de jazz aumenta la utilidad de Neal en una cantidad menor. Al margen, su utilidad
adicional disminuye: Tiene utilidad marginal decreciente.
Las utilidades marginales asociadas al snowboard y al jazz se
ingresan en las columnas 4 y 5 del Cuadro 6.1. Son las
diferencias en los valores totales de utilidad cuando el consumo aumenta en una unidad.
Por ejemplo, cuando Neal realiza una sexta visita a Whistler su utilidad total
aumenta de 260 utils a 292 utils. Su utilidad marginal para la sexta
unidad es, por lo tanto, de 32 utils, tal como se define en la columna 4. A la luz de este
ejemplo, debe quedar claro que podemos definir la utilidad marginal como:
 | (6.1) |
donde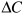 denota el cambio en la cantidad consumida del bien o
servicio en cuestión.
denota el cambio en la cantidad consumida del bien o
servicio en cuestión.
La utilidad marginal es la adición a la utilidad total creada cuando se consume una unidad más de un bien o servicio.
La disminución de la utilidad marginal implica que la adición a la utilidad total de cada unidad extra de un bien o servicio consumido está disminuyendo.
Las utilidades marginales asociadas al consumo de diferentes cantidades de los
dos bienes se grafican en las Figuras 6.3 y 6.4,
utilizando los datos de las columnas 4 y 5 del Cuadro 6.1.
Estas funciones están disminuyendo, como lo indica su pendiente
negativa. También debe quedar claro que las curvas MU pueden derivarse
de las curvas TU. Por ejemplo, en la figura 6.2, al pasar
de 2 unidades a 3 unidades de Jazz, TU aumenta en 34 unidades. Pero 34/1 es
la pendiente de la función TU en este rango de consumo —la
distancia vertical dividida por la distancia horizontal. De igual manera, si el consumo de jazz
aumenta de 4 unidades a 5 unidades el cambio correspondiente en TU es de 24
unidades, nuevamente la distancia vertical dividida por la distancia horizontal, y
así la pendiente de la función. En definitiva, la MU es la pendiente de la
función TU.
Ahora que Neal ha definido sus horarios de servicios públicos, debe considerar el precio
de cada actividad. En definitiva, a la hora de decidir cómo asignar su presupuesto mensual de
entretenimiento, debe evaluar cuánta utilidad obtiene de cada
dólar gastado en snowboard y jazz: ¿Qué “bang por su dinero”
obtiene? Veamos cómo podría hacer para asignar su presupuesto. Cuando
ha gastado completamente su presupuesto de la manera que le va a dar mayor
utilidad, decimos que ha alcanzado el equilibrio, porque no tendrá ningún
incentivo para cambiar sus patrones de gasto.
Si aborda una vez, a un costo de $30, obtiene 72 utils de satisfacción,
que es 2.4 utils por dólar gastado (=72/30). Una visita a un club de jazz le
daría 2.6 utils por dólar (=52/20). Inicialmente, por lo tanto, sus
dólares le dan más utilidad por dólar cuando se gasta en jazz. Su
MU por dólar gastado en cada actividad se da en las dos últimas columnas de
la tabla. Estos valores se obtienen dividiendo la MU asociada a
cada unidad adicional por el precio del bien.
Asumiremos que Neal tiene un presupuesto de $200. Se da cuenta de que su
gasto inicial debe ser en una visita al club de jazz, porque obtiene más utilidad por
dólar que se gasta ahí. Habiendo hecho uno de esos gastos, ve que una segunda
salida de jazz le daría 2.1 utils por dólar gastado, mientras que una primera visita a
Whistler le daría 2.4 utils por dólar. En consecuencia, su segunda
actividad es una salida de snowboard.
Después de haber realizado una visita de jazz y otra de snowboard, decide entonces una
segunda visita al club de jazz por la misma razón que antes: valor de utilidad por su
dinero. Sigue destinando su presupuesto de esta manera hasta
agotar su presupuesto. En nuestro ejemplo, esto ocurre cuando gasta 120 dólares en cuatro salidas de
snowboard y 80 dólares en cuatro visitas a clubes de jazz. En este equilibrio de consumo, obtiene el mismo valor de utilidad por
dólar por la última unidad de cada actividad consumida. Esta es una
condición necesaria para que esté maximizando su utilidad, es decir, para estar en
equilibrio.
El equilibrio del consumidor ocurre cuando la utilidad marginal por dólar gastado en la última unidad de cada bien es igual.
Para estar absolutamente convencido de esto, imagina que Neal había optado en cambio por
abordar dos veces y visitar siete veces los clubes de jazz; esta combinación
también agotaría exactamente su presupuesto de 200 dólares. Con tal asignación, obtendría
2.0 utils por dólar gastado en su salida marginal (segunda) de snowboard, pero
apenas 0.95 utils por dólar gastado en su marginal (séptima) visita al club de jazz. Si, en cambio, fuera a
reasignar su presupuesto a favor del snowboard, obtendría 1.67 utils por
dólar gastado en una tercera visita a los cerros. Al reducir en uno el número de
visitas de jazz, perdería 0.95 utils por dólar reasignado.
En consecuencia, la ganancia de utilidad de una reasignación de su presupuesto hacia el
snowboard superaría la pérdida de servicios públicos por asignar menos dólares
al jazz. Su asignación inicial, por lo tanto, no fue un óptimo, o
equilibrio.
Sólo cuando la utilidad por dólar gastado en cada actividad sea igual al
margen Neal estará optimizando. Cuando esa condición se mantiene, una reasignación no le
beneficiaría, porque las ganancias de un dólar más al
embarcar se compensarían exactamente con la pérdida de un dólar menos gastado en
jazz. Por lo tanto, podemos escribir la condición de equilibrio como
 | (6.2) |
Si bien este ejemplo tiene apenas dos bienes, en el caso más general de muchos
bienes, esta misma condición debe sostenerse para todos los pares de bienes en los
que el consumidor destine su presupuesto.
De la utilidad a la demanda
La teoría de la utilidad es una forma útil de analizar cómo un consumidor toma decisiones.
Pero en el mundo real no observamos la utilidad de un consumidor, ni total
ni marginal. En cambio, su comportamiento en el mercado se observa
a través de la curva de demanda. ¿Cómo se relacionan los servicios públicos y la demanda?
Las funciones de demanda relacionan la cantidad de un bien consumido con el precio de ese
bien, siendo iguales otras cosas. Entonces, rastreemos los efectos de un
cambio de precio bajo demanda, con la ayuda de este marco de utilidad. Vamos a introducir
una simplificación aquí: Los bienes son divisibles, o que vienen en pequeños
paquetes relativos a los ingresos. Piense, por ejemplo, en kilómetros recorridos por
año, o litros de gasolina comprados. Conceptualizar las cosas de esta manera nos
permite imaginar más fácilmente experimentos en los que pequeñas cantidades de un
presupuesto se asignan un dólar a la vez. En contraste, en el ejemplo de
snowboard/jazz, tuvimos que reasignar el presupuesto en bultos de $30 o
$20 a la vez porque no podíamos “fraccionar” estos bienes.
Los efectos de un cambio de precio en la demanda de un consumidor pueden verse a través de la
condición que describe su equilibrio. Si el ingreso se destina a,
digamos, tres bienes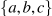 , de tal manera que MU a/P a = MU b/P b = MU c/ P c, y
el precio de, digamos, bueno b cae, el consumidor debe reasignar el presupuesto para
que una vez más se equiparen los MU s por dólar gastado. ¿Cómo hace
esto? Claramente, si compra más o menos de cualquier bien, el MU
cambia. Si el precio del bien b cae, entonces el consumidor inicialmente obtiene más
utilidad del bien b por el último dólar que gasta en él (el
denominador en la expresión MU b/P b cae , y en consecuencia el valor
de la relación se eleva a un valor mayor que los valores de los bienes a y c).
, de tal manera que MU a/P a = MU b/P b = MU c/ P c, y
el precio de, digamos, bueno b cae, el consumidor debe reasignar el presupuesto para
que una vez más se equiparen los MU s por dólar gastado. ¿Cómo hace
esto? Claramente, si compra más o menos de cualquier bien, el MU
cambia. Si el precio del bien b cae, entonces el consumidor inicialmente obtiene más
utilidad del bien b por el último dólar que gasta en él (el
denominador en la expresión MU b/P b cae , y en consecuencia el valor
de la relación se eleva a un valor mayor que los valores de los bienes a y c).
El consumidor responde a esto, en primera instancia, comprando más del bien
más barato. Obtiene más utilidad total como consecuencia, y en el
proceso obtendrá menos utilidad al margen de ese
bien. En esencia, el numerador en la expresión luego cae, para
realinearlo con el precio más bajo. Esta igualdad también proporciona un apuntalamiento
para lo que se llama la ley de la demanda: Más de un bien se
demanda a un precio más bajo. Si cae el precio de algún bien, entonces,
para que se restablezca la condición de equilibrio, también se
debe bajar el MU de ese bien. Dado que MU disminuye cuando se compra más, esto
establece que las curvas de demanda deben inclinarse hacia abajo.
La ley de la demanda establece que, siendo iguales otras cosas, se demanda más bien cuanto menor es su precio.
No obstante, los efectos de una caída de precios suelen estar más extendidos que
esto, debido a que las cantidades de otros bienes consumidos también pueden cambiar. Como
se explicó en capítulos anteriores, la caída en el precio del bien b llevará
al consumidor a adquirir más unidades de bienes complementarios y
menos unidades de bienes que sean sustitutos. Por lo que todo el proceso de
asignación presupuestal debe ser redeterminado en respuesta a cualquier cambio de precio. Pero
al final del día, un nuevo equilibrio debe ser aquel en el que la
utilidad marginal por dólar gastado en cada bien sea igual.
Aplicando la teoría
Las curvas de demanda desarrolladas en el Capítulo 3 pueden estar
relacionadas con el análisis de utilidad anterior. En nuestro ejemplo, Neal compró cuatro
boletos de ascensor en Whistler cuando el precio era de $30. Podemos pensar en esta
combinación como un punto de su curva de demanda, donde las “otras cosas mantenidas
constantes” son el precio del jazz, sus ingresos, sus gustos, etc.
Supongamos ahora que el precio de un boleto de ascensor aumentó a $40. ¿Cómo podríamos
encontrar otro punto en su curva de demanda correspondiente a este precio, utilizando
la información del Cuadro 6.1? La utilidad marginal por
dólar asociada a cada visita a Whistler podría ser recalculada
dividiendo los valores en la columna 4 por 40 en lugar de 30, produciendo una nueva columna
6. Entonces determinaríamos una nueva asignación de su presupuesto entre los dos
bienes que maximizaría la utilidad. Después de tal cálculo encontraríamos
que realiza tres visitas a Whistler y cuatro visitas al club de jazz. Así, la
combinación es otro punto en su curva de demanda. Tenga en cuenta
que esta asignación agota exactamente su presupuesto de 200 dólares.
es otro punto en su curva de demanda. Tenga en cuenta
que esta asignación agota exactamente su presupuesto de 200 dólares.
Al establecer el precio igual a $20, este ejercicio podría realizarse nuevamente,
y el resultado será una cantidad demandada de boletos de ascensor igual a siete
(más tres visitas a clubes de jazz). Así, la combinación es
otro punto en su curva de demanda. La Figura 6.5 traza una curva de
demanda que atraviesa estos tres puntos.
es
otro punto en su curva de demanda. La Figura 6.5 traza una curva de
demanda que atraviesa estos tres puntos.
Al repetir este ejercicio para muchos precios diferentes, se
establece la curva de demanda. Ahora hemos vinculado la curva de demanda a la teoría de la utilidad.
Caja de Aplicación 6.2 Utilidad Individual y Colectiva
El ejemplo que se desarrolla en el texto no está muy lejos de lo que hacen los economistas
en la práctica. Desde un punto de vista filosófico, se supone que los economistas deben estar
interesados en el bienestar de los ciudadanos que conforman una economía o un
país. Para determinar qué tan “acomodados” pueden ser los ciudadanos, los científicos sociales
suelen realizar encuestas sobre cómo son las personas 'contentas' o 'felices' en
su vida cotidiana. Por ejemplo, el Earth Institute de la
Universidad de Columbia produce regularmente un 'World Happiness Report'. El informe se
basa en respuestas a preguntas de encuestas en numerosas economías. Una de las
medidas que utiliza para comparar los niveles de utilidad es la escalera Cantril. Se trata de una escala de
11 puntos que va de 0 a 10, con el valor más bajo significando la
peor vida posible, y 10 la mayor calidad de vida posible. Al
informar sus hallazgos, los investigadores esencialmente están afirmando que algunas
economías tienen, en promedio, más satisfechas o más felices, personas que otras.
La utilidad puede considerarse exactamente de esta manera: Un mayor valor reportado en
la escalera Cantril sugiere una mayor utilidad.
El Índice de Desarrollo Humano de las Naciones
Unidas da una medida ligeramente diferente del bienestar entre las economías. En este caso, los países obtienen una puntuación alta
al tener un alto nivel de ingresos, buena salud (medida por la
esperanza de vida) y altos niveles de educación, medidos por el número de
años de educación concluidos o previstos.
En la práctica, los científicos sociales se sienten muy cómodos utilizando
conceptos basados en la utilidad para describir las circunstancias económicas de individuos en diferentes
economías.
6.3 Elección con utilidad ordinal
La restricción presupuestaria
En el apartado anterior, asumimos que la utilidad es medible para entender
mejor cómo los consumidores asignan sus presupuestos, y cómo este proceso
se refleja en las demandas del mercado que se observan. La creencia de que la
utilidad podría ser medible no es demasiado extrema en la era moderna.
Los neurocientíficos están mapeando cada vez más el cerebro humano y
entendiendo cómo responde a estímulos positivos y negativos. Al mismo
tiempo, numerosas encuestas sociológicas en todo el mundo piden a los individuos que
clasifiquen su felicidad en una escala del uno al diez, o algo similar, con
miras a hacer comparaciones entre la
felicidad a nivel individual y a nivel de grupo — ver Recuadro de Aplicación 6.2.
Sin embargo, no todos los científicos pueden estar convencidos de que debemos
formular reglas de comportamiento sobre esta base. En consecuencia, examinamos ahora la
economía del comportamiento del consumidor sin esta fuerte suposición.
En cambio, asumimos que los individuos son capaces de identificar (a) diferentes combinaciones de
bienes y servicios que producen la misma satisfacción, y (b) combinaciones de
bienes y servicios que producen más satisfacción que otras combinaciones. En
contraste con la utilidad medible (o cardinal), este concepto se llama
utilidad ordinal, porque asume solo que los consumidores pueden ordenar
paquetes de servicios públicos en lugar de cuantificar la utilidad.
La utilidad ordinal supone que los individuos pueden clasificar los paquetes de productos básicos de acuerdo con el nivel de satisfacción asociado con cada paquete.
La restricción presupuestaria
El límite de gastos mensuales de Neal, o restricción presupuestaria, es de
$200. Además, enfrenta un precio de $30 por boletos de ascensor y $20 por
visita a clubes de jazz. Por lo tanto, utilizando S para denotar el número de
salidas de snowboard y J el número de visitas al club de jazz, si gasta todo su
presupuesto debe ser cierto que la suma de gastos en cada actividad
agota su presupuesto o ingresos (I):
Dado que muchas combinaciones diferentes de los dos bienes son asequibles, se
deduce que la restricción presupuestaria define todos los paquetes de bienes que el
consumidor puede pagar con un presupuesto determinado.
La restricción presupuestaria define todos los paquetes de bienes que el consumidor puede permitirse con un presupuesto determinado.
La restricción presupuestaria, entonces, es justo lo que dice ser: un límite en el
comportamiento. La restricción presupuestal de Neal se ilustra en la Figura 6.6,
donde la cantidad de cada bien consumido se da en los
ejes. Si gasta todos sus ingresos de 200 dólares en jazz, puede hacer exactamente diez visitas al club de
jazz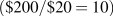 . El cálculo también se aplica a las visitas
a Whistler. El valor de intercepción siempre se obtiene dividiendo los ingresos por
el precio del bien o actividad en cuestión.
. El cálculo también se aplica a las visitas
a Whistler. El valor de intercepción siempre se obtiene dividiendo los ingresos por
el precio del bien o actividad en cuestión.
Además de estos extremos asequibles, Neal también puede permitirse muchos otros
paquetes, por ejemplo, (S =2, J =7), o (S =4, J =4), o (S =6, J =1). El conjunto de combinaciones
factibles, o asequibles, está delimitado por la
línea presupuestal, y esto se ilustra en la Figura 6.6.
El conjunto de bienes y servicios asequibles para el consumidor está delimitado por la línea presupuestal desde arriba; el conjunto no asequible se encuentra estrictamente por encima de la línea presupuestaria.
La pendiente de la línea presupuestal es informativa. Como se ilustra en el Capítulo 1,
indica cuántas visitas de snowboard deben sacrificarse por una visita adicional de
jazz; define las compensaciones del consumidor. Para ilustrar:
Supongamos que Neal está inicialmente en el punto A (J =4, S =4), y se mueve al punto K
(J =7, S =2). Claramente, ambos puntos son asequibles. Al hacer la mudanza,
intercambia dos salidas de snowboard para conseguir tres
visitas adicionales al club de jazz, una compensación de 2/3. Esta compensación es la pendiente de la línea presupuestal
que, en la Figura 6.6, es AB/BK=—2/3, donde el
signo negativo refleja la pendiente descendente.
¿Podría ser que esta relación refleje los dos precios ($20/$30)? La respuesta
es sí: La pendiente de la línea presupuestal viene dada por la
distancia vertical dividida por la distancia horizontal, OF/OC. Los puntos F y C se
obtuvieron dividiendo los ingresos por el precio respectivo; recuerde que la
intercepción del jazz es . Formalmente, es decir I/P J. El intercepto en
el eje del snowboard es igualmente I/P S. En consecuencia, la pendiente de la
restricción presupuestal es:
. Formalmente, es decir I/P J. El intercepto en
el eje del snowboard es igualmente I/P S. En consecuencia, la pendiente de la
restricción presupuestal es:
Dado que la línea presupuestal tiene una pendiente negativa, es técnicamente correcto
definirla con un signo negativo. Pero, como ocurre con las elasticidades,
frecuentemente se omite el signo.
Gustos e indiferencia
Consideramos ahora cómo representar los gustos de un consumidor en dos dimensiones,
dado que puede ordenar, o clasificar, diferentes paquetes de consumo, y que
puede definir una serie de paquetes diferentes que todos producen la misma
satisfacción. Nos limitamos inicialmente a considerar solo “bienes”,
y no “bads” como la contaminación.
La Figura 6.7 examina las implicaciones de estos
supuestos sobre los gustos. Cada punto muestra un paquete de consumo de
snowboard y jazz. Empecemos por el bulto R. Dado que se
prefiere más bien a menos, cualquier punto como L, que se encuentra al noreste de R, se
prefiere a R, ya que L ofrece más de ambos bienes que R. Por el contrario, los puntos
al suroeste de R ofrecen menos de cada bien que R, y por lo tanto
R es preferido a un punto como V.
Sin conocer los gustos del consumidor, no podemos estar seguros en esta etapa de cómo los
puntos en las regiones noroeste y sureste se comparan con R. A W o T, el
consumidor tiene más de un bien y menos del otro que en R. Alguien a quien
realmente le gusta el snowboard podría preferir W a R, pero un aficionado al jazz podría preferir
T a R.
Pidamos ahora a Neal que revele sus gustos, pidiéndole que defina varias
combinaciones de snowboard y jazz que le den exactamente el
mismo grado de satisfacción que la combinación en R. Supongamos además, por
razones que entenderemos en breve, que sus respuestas definen una serie de
puntos que se encuentran en el contorno bellamente suave U R en la Figura 6.8.
Al ser indiferente entre todos los puntos en U R por
construcción, este contorno es una curva de indiferencia.
Una curva de indiferencia define combinaciones de bienes y servicios que producen el mismo nivel de satisfacción para el consumidor.
Siguiendo este experimento, podríamos tomar otros puntos de la Figura 6.8,
como L y V, y pedirle al consumidor que defina paquetes
que arrojarían el mismo nivel de satisfacción, o indiferencia. Estas
combinaciones producirían contornos adicionales, como U L y U V en
la Figura 6.8. Este proceso produce una serie de
curvas de indiferencia que juntas forman un mapa de indiferencia.
Un mapa de indiferencia es un conjunto de curvas de indiferencia, donde las curvas más alejadas del origen denotan un mayor nivel de satisfacción.
Ahora vamos a explorar las propiedades de este mapa, y así entender por qué
los contornos tienen su forma convexa suave. Cuentan con cuatro propiedades. Los tres
primeros se desprenden de nuestra discusión anterior, y el cuarto requiere
investigación.
Las curvas de indiferencia más alejadas del origen reflejan mayores
niveles de satisfacción.
Las curvas de indiferencia están inclinadas negativamente. Esto refleja el
hecho de que si un consumidor obtiene más de un bien debería tener menos del
otro para permanecer indiferente entre las dos combinaciones.
Las curvas de indiferencia no pueden cruzarse. Si dos curvas se
cruzaran en un punto dado, entonces tendríamos dos niveles diferentes de
satisfacción asociados con el mismo paquete de productos básicos, una
imposibilidad.
Las curvas de indiferencia son convexas cuando se ven desde el origen, reflejando
una tasa marginal de sustitución decreciente.
La forma convexa refleja una característica importante de las preferencias: Cuando
los consumidores tienen mucho de algún bien, valoran
menos una unidad marginal que cuando tienen una pequeña cantidad de ese bien. De manera más formal, tienen una valoración marginal
mayor a bajos niveles de consumo, que la primera
taza de café por la mañana brinda mayor satisfacción que la segunda
o tercera taza.
Considera los diversos puntos sobre U R, comenzando en M en la Figura 6.8.
En M Neal tablas de snowboard mucho; en N sube mucho menos.
La forma convexa de su mapa de indiferencia muestra que valora un viaje marginal de
snowboard más en N que en M. Para ver esto, considera lo que sucede a medida que
avanza a lo largo de su curva de indiferencia, comenzando en M. Hemos elegido las
coordenadas en U R para que, en pasando de M a R, y nuevamente de N a H,
la cantidad adicional de jazz es la misma: CR=FH. De M, si Neal pasa a
R, consume una cantidad adicional de jazz, CR. Por definición de la curva de
indiferencia, está dispuesto a renunciar a las salidas de snowboard MC. El ratio
MC/CR define su disposición a sustituir un bien por otro. Esta
relación, al ser una distancia vertical dividida por una distancia horizontal, es la
pendiente de la curva de indiferencia y se denomina tasa marginal
de sustitución, MRS.
La tasa marginal de sustitución es la pendiente de la curva de indiferencia. Define la cantidad de un bien que el consumidor está dispuesto a sacrificar para obtener un incremento dado del otro, manteniendo sin cambios la utilidad.
En N, el consumidor está dispuesto a sacrificar la cantidad NF de embarque para obtener
la misma cantidad adicional de jazz. Tenga en cuenta que, cuando aborde menos,
como en N, está dispuesto a renunciar a menos abordaje que cuando tiene mucho de
él, como en M, para obtener la misma cantidad adicional de jazz. Su
disposición a sustituir disminuye a medida que pasa de M a N: La
cantidad NF es menor que la cantidad MC. Para reflejar esta
característica gustativa, la curva de indiferencia tiene una tasa
marginal de sustitución decreciente: Una pendiente más plana a medida que bajamos por su
superficie.
Una tasa marginal decreciente de sustitución refleja un mayor valor marginal asociado a cantidades menores de cualquier bien consumido.
Optimización
Ahora estamos en condiciones de examinar cómo optimiza el consumidor, cómo llega
al más alto nivel de satisfacción posible. La restricción en su
comportamiento es el conjunto asequible definido en la Figura 6.6, la línea
presupuestaria.
La figura 6.9 muestra varias
curvas de indiferencia de Neal en conjunción con su restricción presupuestal. Proponemos que
maximiza su utilidad, o satisfacción, en el punto E, sobre la
curva de indiferencia denotada por U 3. Si bien puntos como F y G también están en el
límite del conjunto asequible, no arrojan tanta satisfacción como E,
porque E yace en una curva de indiferencia más alta. El
nivel más alto posible de satisfacción se alcanza, por lo tanto, cuando la línea presupuestaria toca
una curva de indiferencia en un solo punto, es decir, donde la restricción
es tangente a la curva de indiferencia. E es tal punto.
Esta tangencia entre la restricción presupuestal y una curva de indiferencia
requiere que las pendientes de cada una sean las mismas en el punto de tangencia. Ya
hemos establecido que la pendiente de la restricción presupuestal es la
negativa de la relación precio (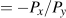 ). La pendiente de la
curva de indiferencia es la tasa marginal de sustitución MRS. De ello se deduce, por tanto,
que el consumidor optimiza donde la tasa marginal de
sustitución iguala la pendiente de la línea de precio.
). La pendiente de la
curva de indiferencia es la tasa marginal de sustitución MRS. De ello se deduce, por tanto,
que el consumidor optimiza donde la tasa marginal de
sustitución iguala la pendiente de la línea de precio.
La optimización requiere:
 | (6.3) |
Un óptimo de consumo ocurre donde el paquete de consumo elegido es un punto tal que la relación precio es igual a la tasa marginal de sustitución.
Observe el parecido entre esta condición y la derivada en la
primera sección como Ecuación 6.2. Allí argumentamos
que el equilibrio requiere que la relación de las utilidades marginales sea la misma que la
relación de precios. Aquí mostramos que el MRS debe igualar la relación de precios.
De hecho, con un poco de matemáticas se puede demostrar que el MRS es efectivamente
el mismo que el (negativo de la) relación de las utilidades marginales:
 . Por lo tanto, ¡las dos condiciones son en esencia las mismas!
Sin embargo, no fue necesario suponer que un individuo pueda realmente
medir su utilidad para obtener el resultado de que el MRS debe igualar la relación
precio en equilibrio. El concepto de utilidad ordinal es suficiente.
. Por lo tanto, ¡las dos condiciones son en esencia las mismas!
Sin embargo, no fue necesario suponer que un individuo pueda realmente
medir su utilidad para obtener el resultado de que el MRS debe igualar la relación
precio en equilibrio. El concepto de utilidad ordinal es suficiente.
Ajustar a los cambios de ingresos
Supongamos ahora que los ingresos de Neal cambian de $200 a $300. ¿Cómo
afectará esto a sus decisiones de consumo? En la Figura 6.10, este
cambio se refleja en un desplazamiento paralelo hacia el exterior de la
restricción presupuestal. Dado que no se produce ningún cambio de precio, la pendiente se mantiene constante. Al
recalcular la relación entre ingresos y precio de cada actividad, encontramos que las
nuevas intercepciones de snowboard y jazz son 10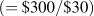 y 15
y 15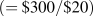 ,
respectivamente. Claramente, el consumidor puede alcanzar un mayor nivel de
satisfacción —en una nueva tangencia a una curva de mayor indiferencia— como
resultado de la ampliación del tamaño del conjunto asequible. En la Figura 6.10,
el nuevo equilibrio se encuentra en E 1.
,
respectivamente. Claramente, el consumidor puede alcanzar un mayor nivel de
satisfacción —en una nueva tangencia a una curva de mayor indiferencia— como
resultado de la ampliación del tamaño del conjunto asequible. En la Figura 6.10,
el nuevo equilibrio se encuentra en E 1.
Ajustar a los cambios de precios
A continuación, considere el impacto de un cambio de precio desde el equilibrio inicial E 0
en la Figura 6.10. Supongamos que el jazz ahora cuesta más. Esto
reduce el poder adquisitivo del presupuesto dado de $200. Por lo tanto, se reduce la nueva
intercepción de jazz. La restricción presupuestal
se vuelve más pronunciada y gira alrededor de la intercepción de snowboard H, que
no cambia porque su precio es constante. El nuevo equilibrio se encuentra en E 2,
lo que refleja un menor nivel de satisfacción debido a que el conjunto asequible
se ha visto reducido por el incremento del precio. Como se explica en la Sección 6.2,
E 0 y E 2 definen puntos en la
curva de demanda para el jazz (J 0 y J 2): Reflejan la respuesta del consumidor ante un
cambio en el precio del jazz con todas las demás cosas mantenido constante. En
contraste, el incremento de precios del jazz cambia la curva de demanda para el
snowboard: En lo que respecta a la curva de demanda para el snowboard, un
cambio en el precio del jazz es una de esas cosas distintas al propio precio que
determinan su posición.
Filantropía
Los particulares en el análisis anterior tienen como objetivo maximizar su utilidad, dado
que cuentan con un presupuesto fijo. Tenga en cuenta que esta suposición conductual
no descarta la posibilidad de que estos mismos individuos puedan ser
filantrópicos —es decir, obtengan utilidad del acto de dar a su organización benéfica
favorita o a United Way o Centre-aide. Para ver esto supongamos que las
donaciones dan utilidad al individuo en cuestión —obtiene una sensación de
'brillo caliente' como resultado de dar, es decir, obtiene utilidad de
la actividad. No hay razón para que no podamos poner donaciones caritativas en
un eje y algún otro bien o combinación de bienes en el eje restante.
En equilibrio, la utilidad marginal por dólar de las contribuciones a la caridad
debe ser igual a la utilidad marginal por dólar de gasto en otros bienes;
o bien, expresada en términos de utilidad ordinal, la tasa marginal de sustitución
entre filantropía y cualquier otro bien debe ser igual a la relación de sus
precios. Evidentemente el precio de un dólar de donaciones caritativas es de un
dólar.
6.4 Aplicaciones del análisis de indiferencia
Impactos en los precios: Complementos y sustitutos
La naturaleza de los complementos y sustitutos, definidos en el Capítulo 4, se
puede entender mejor con la ayuda de la Figura 6.10.
El nuevo equilibrio E 2 se ha dibujado de manera que el
incremento en el precio del jazz da como resultado más snowboard—la cantidad de
S aumenta a S 2 desde S 0. Estos bienes son sustitutos en esta
imagen, porque el snowboard aumenta en respuesta a un incremento en el precio del jazz. Si el nuevo equilibrio E 2 estuviera en un punto
dando un nivel menor de S que S 0, concluiríamos que eran
complementos.
Elasticidades de precios cruzados
Continuando con el mismo incremento de precios en el jazz, podríamos calcular el cambio
porcentual en la cantidad de snowboard demandada como
resultado del cambio porcentual en el precio del jazz. En este ejemplo,
el resultado sería un valor de elasticidad positivo, porque el cambio de cantidad
en el snowboard y el cambio de precio en el jazz están ambos en la misma dirección, siendo
cada uno positivo.
Política: Transferencias de ingresos y subsidios de precios
Las políticas gubernamentales que mejoran el poder adquisitivo de
los hogares de bajos ingresos se presentan en dos formas principales: Puras transferencias de ingresos y
subsidios de precios. Los pagos de Asistencia Social (“bienestar”) o prestaciones del Seguro de
Empleo, por ejemplo, proporcionan un incremento en los ingresos
a los necesitados. Los subsidios, por otro lado, permiten a las personas adquirir
determinados bienes o servicios a un precio más bajo, por ejemplo,
subsidios de renta o guarderías.
A diferencia de los impuestos, que reducen el poder adquisitivo del
consumidor, los subsidios y las transferencias de ingresos incrementan el poder adquisitivo.
El impacto de una transferencia de ingresos, en comparación con un subsidio de precio puro, puede
analizarse mediante las Figuras 6.11 y 6.12.
En la Figura 6.11, una transferencia de ingresos incrementa
los ingresos de I 1 a I 2. El nuevo equilibrio en E 2 refleja un
incremento en la utilidad y un incremento en el consumo tanto de
guarderías como de otros bienes.
Supongamos ahora que una administradora de programas de gobierno decide que, si bien
ayuda a esta persona a adquirir más acuerdos de guardería con
la intención de la transferencia, no pretende que el dinero del gobierno se utilice para
comprar otros bienes. Por lo tanto, decide que un
programa de subsidio de guardería podría cumplir mejor con este objetivo que una transferencia pura de ingresos.
Un subsidio de guardería reduce el precio de la guardería y, por lo tanto, gira
la restricción presupuestal hacia afuera alrededor de la intersección en el eje vertical.
En el equilibrio de la Figura 6.12, las compras de otros
bienes cambian muy poco, por lo que la mayor parte del
poder adquisitivo adicional se destina a la guardería.
Llevemos el ejemplo una etapa más allá. A partir del equilibrio inicial
 en la Figura 6.12, supongamos que, en lugar de un subsidio
que llevó al individuo
en la Figura 6.12, supongamos que, en lugar de un subsidio
que llevó al individuo , dimos una transferencia de ingresos que
permitió al consumidor adquirir la combinación
, dimos una transferencia de ingresos que
permitió al consumidor adquirir la combinación . Dicha transferencia
se representa en la Figura 6.13 por un
desplazamiento paralelo hacia el exterior de la restricción
. Dicha transferencia
se representa en la Figura 6.13 por un
desplazamiento paralelo hacia el exterior de la restricción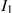 presupuestal de a
presupuestal de a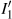 ,
pasando por el punto
,
pasando por el punto . Ahora tenemos una política de
subsidios y una política alternativa de transferencia de ingresos, cada una permitiendo
el mismo paquete de consumo (
. Ahora tenemos una política de
subsidios y una política alternativa de transferencia de ingresos, cada una permitiendo
el mismo paquete de consumo ( ). El aspecto interesante de este par
de posibilidades es que la transferencia de ingresos permitirá al consumidor
alcanzar un mayor nivel de satisfacción —por ejemplo, en un punto
). El aspecto interesante de este par
de posibilidades es que la transferencia de ingresos permitirá al consumidor
alcanzar un mayor nivel de satisfacción —por ejemplo, en un punto — y también la inducirá a consumir más del bien en el
eje vertical. El mayor nivel de satisfacción se produce porque el consumidor tiene
más latitud para asignar los ingresos reales adicionales.
— y también la inducirá a consumir más del bien en el
eje vertical. El mayor nivel de satisfacción se produce porque el consumidor tiene
más latitud para asignar los ingresos reales adicionales.
Solicitud Box 6.3 Subsidios de guardería en Quebec
El gobierno provincial de Quebec subvenciona fuertemente la guardería. En la red del sector público denominada “Centros de la petite enfance”, las familias pueden colocar a sus hijos en guarderías por menos de 10 dólares diarios, mientras que a las familias que utilizan el sector privado se les permite una generosa desgravación fiscal por sus costos de guardería. Esta política está diseñada para permitir que los hogares limiten la parte de sus ingresos gastados en guarderías. Se describe en la Figura 6.13.
Las consecuencias de una fuerte subvención no son despreciables: Exceso de demanda, hasta tal punto que frecuentemente se coloca a los niños en listas de espera para guarderías mucho antes de que sus padres tengan la intención de utilizar el servicio. Los costos anuales del subsidio ascienden a casi 2 mil millones de dólares anuales. Al mismo tiempo, se ha estimado que la política ha permitido que muchos más padres ingresen a la fuerza laboral de lo que de otra manera lo hubiera hecho.
El precio de dar
Imagínese ahora que lo bueno en el eje horizontal son las donaciones caritativas,
más que la guardería, y el gobierno decide que por cada dólar dado
el individuo verá una reducción en su impuesto sobre la renta de 50 centavos. Esto
equivale a reducir a la mitad el 'precio' de las donaciones, porque una donación
de un dólar cuesta ahora la mitad individual de esa cantidad. Gráficamente, la restricción
presupuestaria gira hacia afuera con la intersección vertical sin cambios.
Dado que las donaciones ahora cuestan menos el individuo ha aumentado el poder adquisitivo como
resultado de la reducción del precio de las donaciones. La reducción de precio está
diseñada para aumentar el atractivo de las donaciones a la utilidad
maximizando al consumidor.















