2.1.2: Gráficas de Funciones Cuadráticas

Última actualización
Guardar como PDF

Page ID: 108728

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Gráficas de Funciones Cuadráticas

En lecciones anteriores, hemos discutido la forma estándar de una función cuadrática: f (x) =ax ² +bx+c Puede que hayas visto otras formas, como la forma de vértice, o la forma factorizada. ¿Por qué hay tantas formas comunes de escribir las mismas ecuaciones? ¿Por qué deberíamos aprender todas estas formas diferentes si la forma estándar es la más común de todos modos?

Graficar funciones cuadráticas

Funciones cuadráticas

Una función f definida por f (x) =ax ² +bx+c, donde a, b y c son números reales y a≠ 0, se denomina función cuadrática.

La característica definitoria de una función cuadrática es que es un polinomio cuyo exponente más alto es 2.

Hay varias formas de escribir funciones cuadráticas:

forma estándar, la forma de la función cuadrática anterior: f (x) =ax ² +bx+c
forma de vértice, comúnmente utilizada para bocetos rápidos: f (x) =a (x−h) ² +k
forma factorizada, excelente para encontrar x -intercepciones: f (x) =a (x−r ₁) (x−r ₂)

La intercepción y− de una función cuadrática en forma estándar es (0, c) y se encuentra sustituyendo por x en f (x) =ax ² +bx+c.

Resumen de Vertex Form

Dada una función cuadrática en forma de vértice: f (x) =a (x−h) ² +k:

El vértice está en (h, k)
La parábola se abre si a>0
La parábola se abre si a<0
La parábola es más estrecha que y=x ² si |a|>1
La parábola se abre más ancha que y=x ² si |a|<1

Vértice de una parábola

En la forma estándar de una función cuadrática, la coordenada x del vértice de la parábola viene dada por la ecuación:

\(\ x=-\frac{b}{2 a}\)

La coordenada y del vértice se encuentra con:

\(\ y=f\left(-\frac{b}{2 a}\right)\)

Eje de simetría de una parábola

Una parábola tiene simetría reflectante alrededor de una línea vertical a través del vértice.

La línea vertical\(\ x=-\frac{b}{2 a}\) es también el eje de simetría de la parábola.

Ejemplos

Ejemplo 1

Gráfica g (x) =x ² +6x+7 usando transformaciones.

Solución

Primero, completa el cuadrado para escribir esta función en forma de vértice. Suma y resta\(\ \left(\frac{b}{2}\right)^{2}\) al lado derecho de la ecuación:

g (x) =x ² +6x+7

=x ² +6x+9+7−9

Ahora, factorizar el lado derecho:

g (x) = (x+3) ² −2

Así, a=1 y el vértice de esta parábola es (-3, -2). Sabemos que la parábola se abre con el mismo ancho que y=x ² y tiene un valor mínimo en el vértice. A continuación se muestra la gráfica de la parábola.

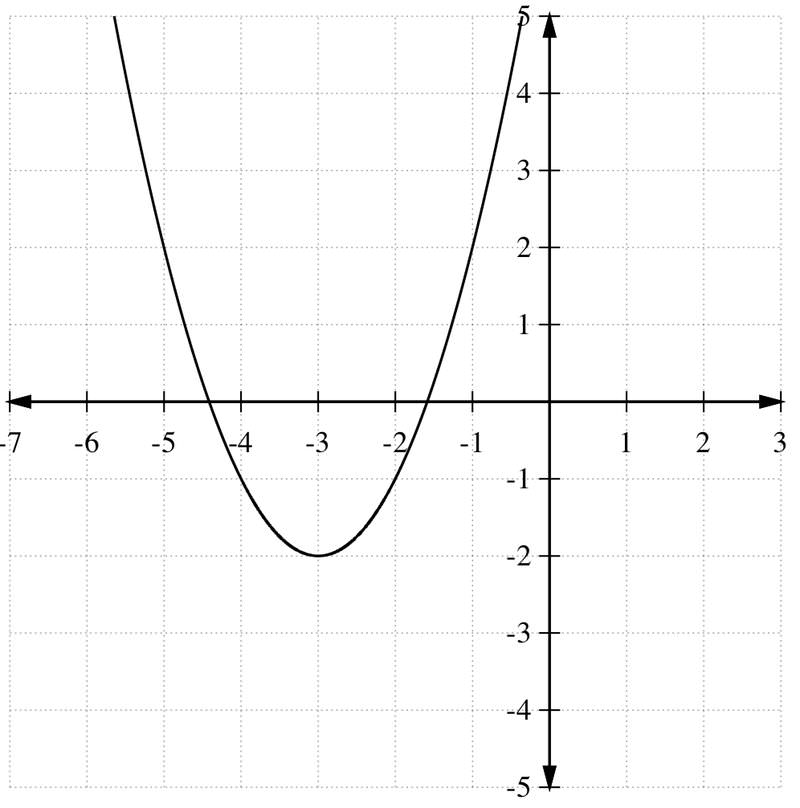
F-d_b5355b73c804c84da9989ac299c220edfd8fce277cd15962a7c289d9+image_tiny+image_tiny.jpg

Ejemplo 2

Encuentra el vértice y grafica la función cuadrática g (x) =x ² −8x+12.

Solución

La coordenada x del vértice es\(\ x=-\frac{-8}{2}=4\).

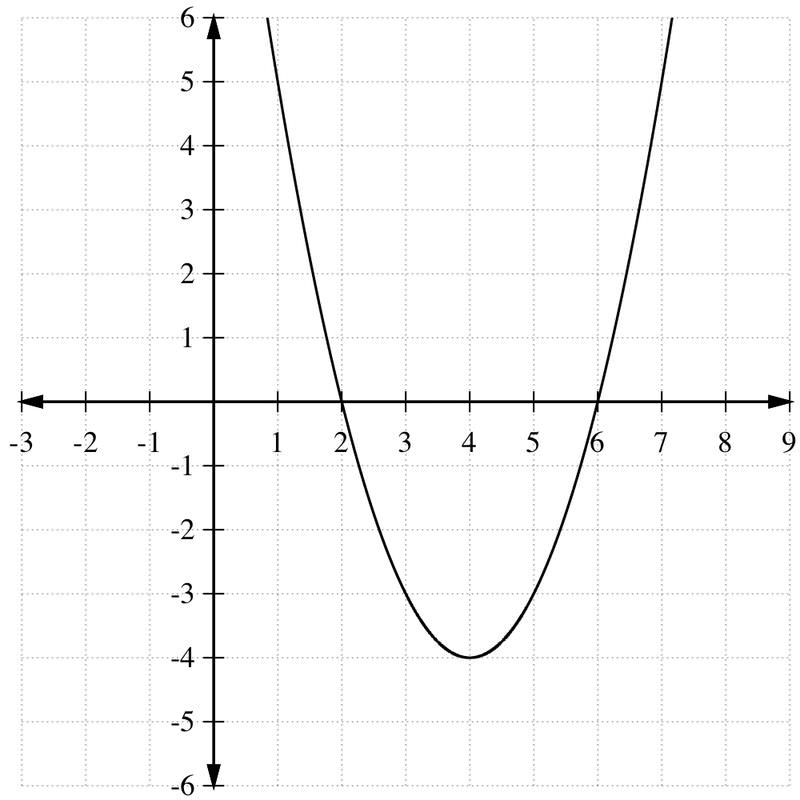
La coordenada y del vértice es g (4) = (4) ² −8 (4) +12=16−32+12=−4

Así el vértice está en (4, -4).

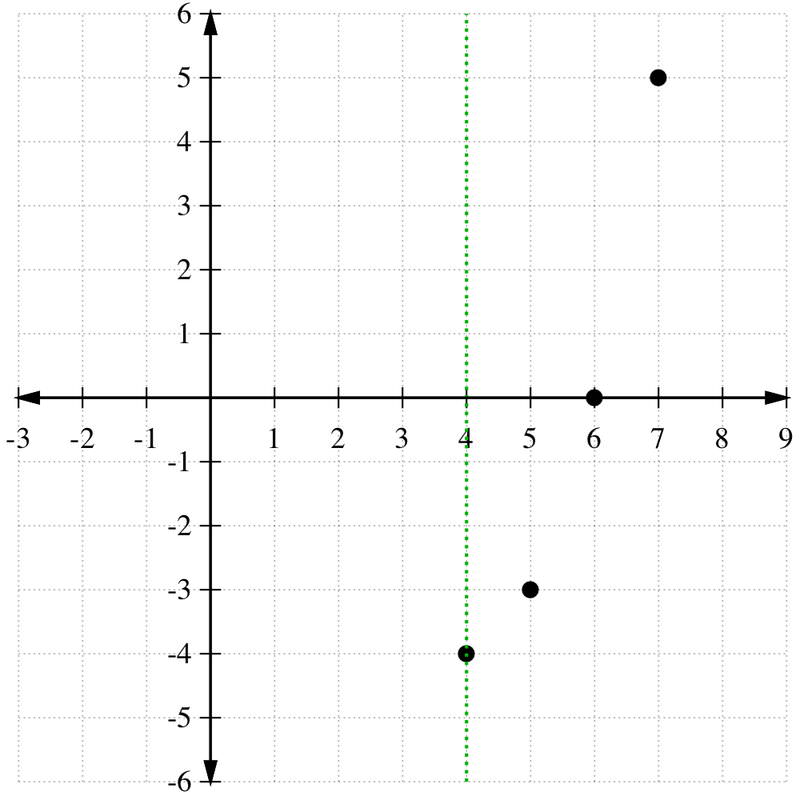
Para graficar la parábola, haremos una tabla de puntos mirando fijamente con la coordenada x de 4:

x	y=g (x)
4	-4
5	-3
6	0
7	5

F-D_45539f6668cc2d67ed5a73972249d196e68558b02b7591297505153d+image_tiny+image_tiny.jpg

Ahora podemos usar la simetría de g (x) para rellenar esta tabla para g (3). Obsérvese que g (3) =g (5) =−3. Asimismo, g (2) =g (6) =0. La gráfica final se encuentra a continuación.

F-d_6409b060700c3ca3f4390058bcbbea9e2ad60240f567f2bf3e866b32+image_tiny+image_tiny.jpg

Ejemplo 3

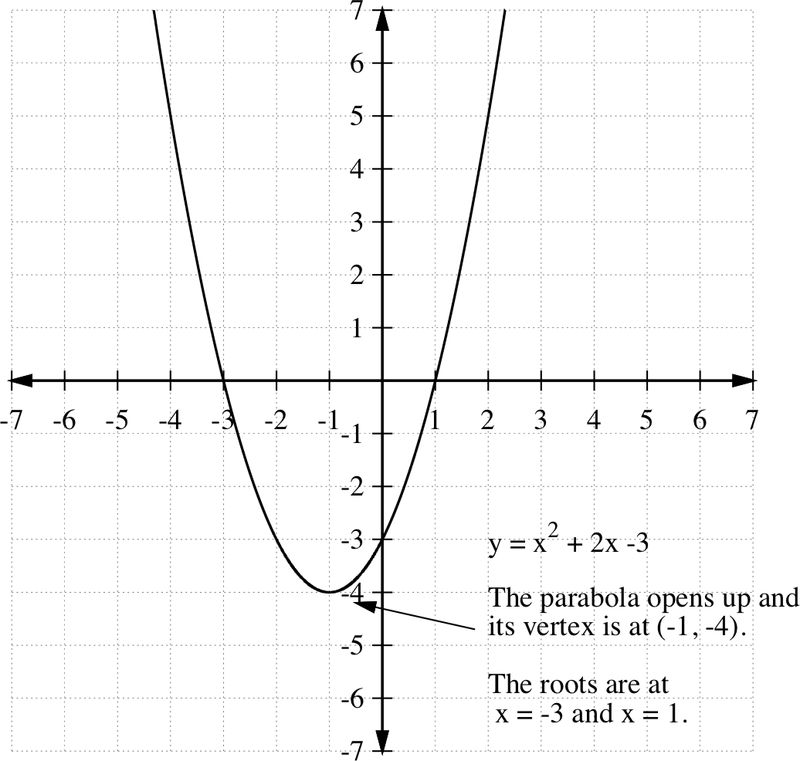
Dibuja el gráfico de la función y=f (x) =x ² +2x−3.

Solución

Primero encontremos las intercepciones. Para el y−intercept, si x=0, entonces f (0) =−3, o y=−3, entonces el punto y−intercept es (0, -3).

Ahora, para las intercepciones x−, si y=f (x) =0, entonces x ² +2x−3=0, o x ² +2x−3 =( x+3) (x−1) =0

de manera que x=−3 y x=1 son las intercepciones x−, es decir (-3, 0) y (1, 0).

El vértice (punto extremo) está en

\(\ x=\frac{-b}{2 a}=\frac{-2}{2(1)}=-1\)

Desde

\ (\\ begin {alineado}
f (-1) & =( -1) ^ {2} +2 (-1) -3\\
&=-4
\ end {alineado}\)

El vértice es (-1, -4).

Dado que el coeficiente de x ² es positivo, a>0, el punto extremo es mínimo y la parábola se abre. A partir de esta información, podemos hacer un boceto aproximado de la parábola que contiene los puntos determinados anteriormente. Observe que el rango de la función es y≥−4.

F-d_883851f2958f4319065de5b55c3fd00494069798f628274ded2901be+image_tiny+image_tiny.jpg

Ejemplo 4

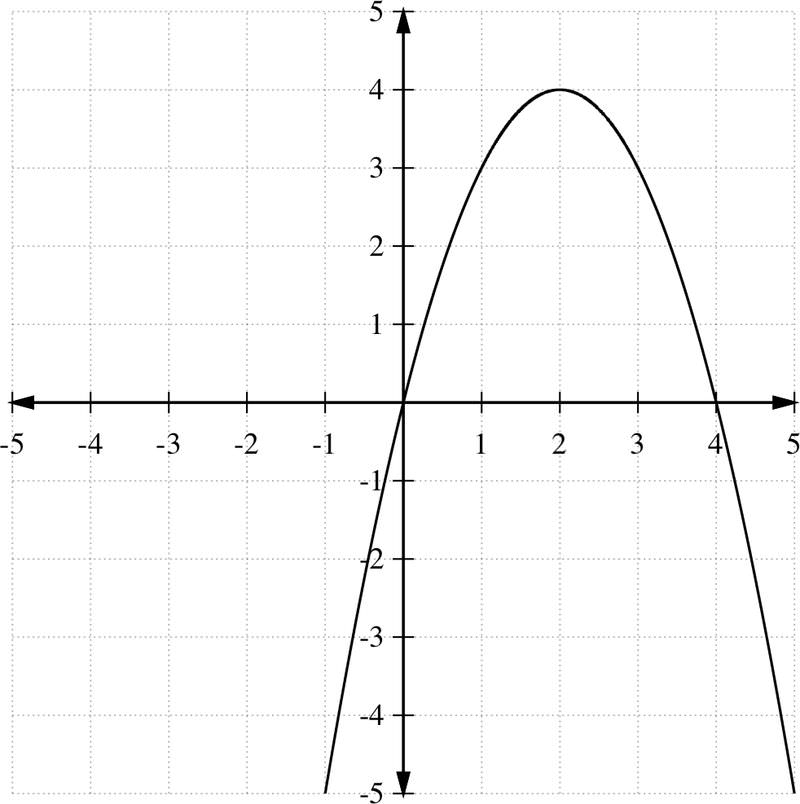
Dibuja el gráfico de la función cuadrática f (x) =−x ² +4x.

Solución

Para encontrar la intersección y−, establezca x=0 y f (0) =− (0) ² +4 (0) =0

Así, la parábola intercepta el eje y en el origen.

El x−intercept se obtiene estableciendo y=0. Así, −x ² +4x=0.

Factoraje,

−x ² +4x=−x (x−4) =0

de modo que x=0 y x=4 son las intercepciones x−.

Tenemos a=−1 y b=4, de modo que el punto extremo ocurre cuando

\(\ x=\frac{-b}{2 a}=\frac{-4}{2(-1)}=2\)

Dado que f (2) =− (2) ² +4 (2) =−4+8=4, entonces (2, 4) es el punto extremo. Es un punto máximo ya que a=−1<0 y la parábola se abre hacia abajo. Finalmente, la gráfica se puede obtener dibujando una parábola a través de los puntos determinados anteriormente. A partir de la gráfica, el rango de la función es y≤4.

F-d_5175b6dee29a23369848e34ac48458c519de4b7d087142019d3a3e96+image_tiny+image_tiny.jpg

Ejemplo 5

Esboce la gráfica de y=−3 (x−2) ² +1.

Solución

La ecuación y=−3 (^x−2) 2+1 ya está en forma de vértice, por lo que graficar es relativamente fácil:

Recordemos el cuando la ecuación está escrita en forma de vértice así, el vértice es el punto (h, k):

forma de vértice: y=a (x−h) ² +k

Nuestra ecuación: y=−3 (x−2) ² +1

Examinando nuestra ecuación, podemos ver que el vértice de la parábola está en (2, 1).

Para encontrar otro punto en la parábola resolver por un valor x.

Como el vértice está en x = 2, probemos una unidad a la derecha: x = 3.

−3 (3−2) ² +1=−2

* Hay un punto en la parábola en (3, -2)

Dado que una parábola tiene un eje de simetría que pasa por su vértice, podemos reflejar el punto (3, -2) a través del eje de simetría para obtener otro punto, (1, -2) también en la parábola.

A continuación se muestra la gráfica de y=−3 (x−2) 2+1, utilizando vértice (2, 1) y puntos (3, -2) y (1, -2).

Revisar

¿Cómo se llama la gráfica en forma de U de una función cuadrática?
¿Qué dirección abre una parábola si el coeficiente principal (a) es positivo?
Para y ² =x Si el coeficiente de y es positivo, ¿de qué manera se abre la parábola?
Cuál es el nombre del punto más bajo de una parábola que se abre y el punto más alto de una parábola que se abre hacia abajo.
¿Cuál es el nombre de la línea que pasa por el vértice que divide la parábola en dos partes simétricas?
Esbozar la gráfica de y=x ² +3
Esbozar el gráfico de y=−x ² +4x−4
Esbozar la gráfica de y=2x ² +8x
Considera la siguiente función cuadrática: y=−x ² −2x+1 a) ¿Qué dirección abre? b) ¿Qué es el vértice? c) ¿Se estira de alguna manera?
Considera las funciones cuadráticas: y=2x ² y=4x ² y=6x ² ¿Qué función cuadrática esperarías tener la parábola más estrecha? Explica tu respuesta.

Esbozar la gráfica de cada función:

y=−x ²
y=3x ² +6x+1
y=12x ² +2x+4
y= (x−3) ² +4
y=−x ² −8x−17

La función cuadrática y=−0.05x ² +1.5x se puede utilizar para representar la trayectoria de un balón de fútbol pateado 30 yardas por el campo. La variable x representa la distancia, en yardas, la pelota ha recorrido por el campo. La altura, en yardas, del balón en el aire está representada por la variable (y).

Utilice la función cuadrática para calcular la altura de la pelota a medida que se desplaza por el campo. Redondea tus respuestas a la centésima de yarda más cercana.

Distancia por el campo (yds)	Altura en el aire (yardas)
0.0
5.0
10.0
15.0
20.0
25.0
30.0

¿Cuál es la altura máxima del balón durante la patada?
¿Qué tan abajo del campo ha recorrido el balón cuando alcanza su máxima altura?
Usa la información de la tabla para graficar la trayectoria de la patada de futbol.
Si solo te mostraran la gráfica de esta función cuadrática, ¿cómo podrías determinar la altura máxima del balón durante el saque y qué tan abajo del campo ha recorrido el balón cuando alcanza su altura máxima?

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 2.2.

El vocabulario

Término	Definición
eje de simetría	El eje de simetría de una parábola es una línea vertical que pasa por el vértice de la parábola. La parábola es simétrica sobre esta línea.
forma factorizada	La forma factorizada de una función cuadrática f (x) es f (x) =a (x−r ₁) (x−r ₂), donde r ₁ y _r2 son las raíces de la función.
Interceptar	Las intercepciones de una curva son las ubicaciones donde la curva interseca los ejes x e y. Una intersección x es un punto en el que la curva cruza el eje x. Una intersección y es un punto en el que la curva cruza el eje y.
Máximo	El máximo es el punto más alto de una gráfica. El máximo arrojará el mayor valor del rango.
Máximo/Mínimo	El máximo es el punto más alto de una función y el mínimo es el punto más bajo de una función.
Mínimo	El mínimo es el punto más bajo de una gráfica. El mínimo arrojará el valor más pequeño del rango.
Parábola	Una parábola es la forma característica de una gráfica de función cuadrática, que se asemeja a una “U”.
función cuadrática	Una función cuadrática es una función que se puede escribir en la forma f (x) =ax ² +bx+c, donde a, b y c son constantes reales y a≠ 0.
forma estándar	La forma estándar de una función cuadrática es f (x) =ax ² +bx+c.
Transformaciones	Las transformaciones se utilizan para cambiar la gráfica de una función padre en la gráfica de una función más compleja.
Vertex	El vértice de una parábola es el punto más alto o más bajo en la gráfica de una parábola. El vértice es el punto máximo de una parábola que se abre hacia abajo y el punto mínimo de una parábola que se abre hacia arriba.
Forma de vértice	La forma de vértice de una función cuadrática es y=a (x−h) ² +k, donde (h, k) es el vértice de la parábola.