3.5.5: Funciones logísticas
- Page ID
- 108495
Funciones logísticas
El crecimiento exponencial aumenta sin ataduras. Esto es razonable para algunas situaciones; sin embargo, para las poblaciones suele haber algún tipo de límite superior. Esto puede ser causado por limitaciones en los alimentos, el espacio u otros recursos escasos. El efecto de este límite superior limitante es una curva que crece exponencialmente al principio y luego se ralentiza y apenas crece en absoluto. Este tipo de crecimiento se llama crecimiento logístico. ¿Cuáles son algunas otras situaciones en las que el crecimiento logístico sería un modelo apropiado?
Funciones logísticas
El crecimiento logístico se puede describir con una ecuación logística. La ecuación logística es de la forma:
\(\ f(x)=\frac{c}{1+a \cdot b^{x}}\)
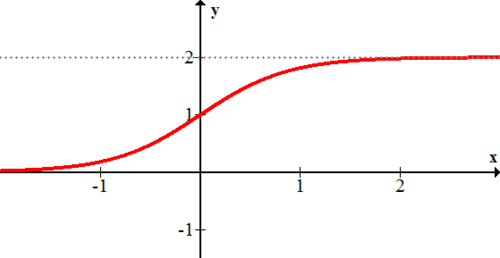
La siguiente función logística tiene una capacidad de carga de 2 que se puede observar directamente a partir de su gráfica.
\(\ f(x)=\frac{2}{1+0.1^{x}}\)
 [Figura1]
[Figura1]Una nota importante sobre la función logística es que tiene un punto de inflexión. De la gráfica anterior se puede observar que en el punto (0, 1) la gráfica pasa de curvar hacia arriba (cóncava hacia arriba) a curvar hacia abajo (cóncava hacia abajo). Este cambio de curvatura se estudiará más en el cálculo, pero por ahora es importante saber que el punto de inflexión ocurre a medio camino entre la capacidad de carga y el eje x.
Ejemplos
Anteriormente, se le preguntó para qué situaciones es apropiado el modelo logístico.
Solución
El modelo logístico es apropiado siempre que el recuento total tenga un límite superior y el crecimiento inicial sea exponencial. Ejemplos son la propagación de rumores y enfermedades en una población limitada y el crecimiento de bacterias o población humana cuando los recursos son limitados.
Se está difundiendo un rumor en una escuela que tiene una población estudiantil total de 1200. Cuatro personas conocen el rumor cuando empieza y tres días después trescientas personas conocen el rumor. ¿De cuántas personas en la escuela conocen el rumor para el cuarto día?
Solución
En una población limitada, el recuento de personas que conocen un rumor es un ejemplo de una situación que se puede modelar utilizando la función logística. La población es de 1200 por lo que esta será la capacidad de carga.
Información identificativa: c=1200; (0,4); (3,300). Primero, use el punto (0, 4) para resolver para a.
\ (\\ comenzar {alineado}
\ frac {1200} {1+a\ cdot b^ {0}} &=4\\
\ frac {1200} {1+a} &=4\\
\ frac {1200} {4} &=1+a\\
a &=299
\ end {alineado}\)
A continuación, utilice el punto (3, 300) para resolver para b.
\ (\\ comenzar {alineado}
\ frac {1200} {1+299\ cdot b^ {3}} &=300\\
4 &=1+299 b^ {3}\
\ frac {3} {299} &=b^ {3}\\
0.21568 &\ aprox b
\ final {alineado}\)
La ecuación de modelado en x=4:
\(\ f(x)=\frac{1200}{1+299 \cdot 0.21568^{x}} \rightarrow f(4) \approx 729 \text { people }\)
Un patrón de crecimiento similar existirá con cualquier tipo de enfermedad infecciosa que se propague rápidamente y sólo pueda infectar a una persona o animal una vez.
Un tipo especial de algas se cultiva en tanques gigantes de plástico transparente y se puede cosechar para hacer biocombustible. A las algas se les da mucha comida, agua y luz solar para crecer rápidamente y el único recurso limitante es el espacio en el tanque. Las algas se cosechan cuando 95% del tanque está lleno dejando el tanque 5% lleno de algas para reproducirse y rellenar el tanque. Actualmente el tiempo entre cosechas es de veinte días y la rentabilidad es de 90% de cosecha. ¿Recomendarías un horario de cosecha más óptimo?
Solución
Identificar cantidades conocidas y modelar el crecimiento de las algas.
Cantidades conocidas: (0,0.05); (20,0.95); c=1 o 100%
\ (\\ comenzar {alineado}
0.05 &=\ frac {1} {1+a\ cdot b^ {0}}\\
1+a &=\ frac {1} {0.05}\\
a &=19\\
0.95 &=\ frac {1} {1+19\ cdot b^ {20}}\\
1+19\ cdot b^ {20} &=\ frac {1} {0.95}\\
b^ {20} &=\ frac {\ left (\ frac {1} {0.95 } -1\ derecha)} {19}\\
b &\ aprox 0.74495
\ fin {alineado}\)
El modelo para el crecimiento de algas es:
\(\ f(x)=\frac{1}{1+19 \cdot(0.74495)^{x}}\)
La pregunta pregunta sobre el horario óptimo de cosecha. Actualmente la cosecha es de 90% por 20 días o una tasa unitaria de 4.5% por día. Si acortas el tiempo entre cosechas donde las algas están creciendo de manera más eficiente, entonces potencialmente esta tasa unitaria podría ser mayor. Supongamos que deja el 15% de las algas en el tanque y cosechas cuando alcanza el 85%. ¿Cuánto tiempo tardará eso en rendir 70%?
\ (\\ comenzar {alineado}
0.15 &=\ frac {1} {1+19\ cdot (0.74495) ^ {x}}\\
x_ {1} &\ aprox 4.10897\\
0.85 &=\ frac {1} {1+19\ cdot (0.74495) ^ {x}}\\
x_ {2} &\ aproximadamente 15.8914\
x_ {2} -x_ {1}\ aprox & 15.8914-4.10897\ aprox 11.78
\ end {alineado}\)
Se necesitan alrededor de 12 días para que los lotes rindan 70% de cosecha que es una tasa unitaria de aproximadamente 6% por día. Esto supone un incremento significativo en la eficiencia. Un programa de cosecha que maximiza el tiempo donde la curva logística es más pronunciada crea el crecimiento global de algas más rápido.
Determinar el modelo logístico dado c=12 y los puntos (0, 9) y (1, 11).
Solución
Los dos puntos dan dos ecuaciones, y el modelo logístico tiene dos variables. Utilice estos puntos para resolver para a y b.
\ (\\ comenzar {alineado}
9 &=\ frac {12} {1+a\ cdot b^ {0}}\\
1+a &=\ frac {12} {9}\\
a &=\ frac {1} {3}\
11 &=\ frac {12} {1+\ izquierda (\ frac {1} {3}\ derecha)\ cdot b^ {1}}\\
1+\ izquierda (\ frac {1} {3}\ derecha)\ cdot b &=\ frac {12} {11}\\
b &=0. \ overline {27} =\ frac {3} {11}
\ end {alineado}\)
Así, el modelo aproximado es:
\(\ f(x)=\frac{12}{1+\left(\frac{1}{3}\right) \cdot\left(\frac{3}{11}\right)^{x}}\)
Determinar el modelo logístico dado c=7 y los puntos (0, 2) y (3, 5).
Solución
Los dos puntos dan dos ecuaciones, y el modelo logístico tiene dos variables. Usa estos dos puntos para resolver para a y b.
\ (\\ comenzar {alineado}
2 &=\ frac {7} {1+a}\\
1+a &=\ frac {7} {2}\\
a &=2.5\\
5 &=\ frac {7} {1+ (2.5)\ cdot b^ {3}}\\
1+ (2.5)\ cdot b^ {3} &=\ frac {7} {5}\
b^ {3} &=0.16\\
b &\ aprox 0.5429
\ end {alineado}\)
Así, el modelo aproximado es:
\(\ f(x)=\frac{7}{1+(2.5) \cdot(0.5429)^{x}}\)
Revisar
Para 1-5, determinar el modelo logístico dada la capacidad de carga y dos puntos.
1. c=12; (0,5); (1,7)
2. c=200; (0,150); (5,180)
3. c=1500; (0,150); (10,1000)
4. c=1000000; (0,100000); (−40,20000)
5. c=30000000; (−60,10000); (0,8000000)
Para 6-8, utilice la función logística\(\ f(x)=\frac{32}{1+3 e^{-x}}\).
6. ¿Cuál es la capacidad de carga de la función?
7. ¿Cuál es la intercepción y de la función?
8. Usa tus respuestas a 6 y 7 junto con al menos dos puntos en la gráfica para hacer un boceto de la función.
Para el 9-11, utilice la función logística\(\ g(x)=\frac{25}{1+4 \cdot 0.2^{x}}\).
9. ¿Cuál es la capacidad de carga de la función?
10. ¿Cuál es la intercepción y de la función?
11. Usa tus respuestas a 9 y 10 junto con al menos dos puntos en la gráfica para hacer un boceto de la función.
Para 12-14, utilice la función logística\(\ h(x)=\frac{4}{1+2 \cdot 0.68^{x}}\).
13. ¿Cuál es la intercepción y de la función?
14. Usa tus respuestas a 12 y 13 junto con al menos dos puntos en la gráfica para hacer un boceto de la función.
15. Dar un ejemplo de una función logística que está disminuyendo (modelos decaimiento). En general, ¿cómo se puede saber a partir de la ecuación si la función logística está aumentando o disminuyendo?
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 3.7.
El vocabulario
| Término | Definición |
|---|---|
| capacidad de carga | La capacidad de carga es la población máxima sustentable que apoyarán los factores ambientales. En otras palabras, es el límite poblacional. |
| función logística | Una función logística es aquella que crece o decae rápidamente por un período de tiempo y luego se nivela. Toma la forma\(\ f(x)=\frac{c}{1+a \cdot b^{x}}\). |
| modelo logístico | Un modelo logístico se utiliza para representar una función que crece o decae rápidamente por un período de tiempo y luego se nivela. |
Atribuciones de imagen
- [Figura 1]
Crédito: Fundación CK-12; CK-12
Fuente: CK-12
Licencia: CC BY-SA

