6.1.1: Elipses Centradas en el Origen
- Page ID
- 108798
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Elipses Centradas en el Origen
Tu tarea es dibujar la elipse\(\ 16 x^{2}+4 y^{2}=144\). ¿Dónde se ubicarán los focos de tu gráfica?
Elipses Centradas en el Origen
La tercera sección cónica es una elipse. Recordemos que un círculo es cuando un plano se corta a través de un cono y ese plano es paralelo a la base del cono. Se forma una elipse cuando ese plano no es paralelo a la base. Por lo tanto, un círculo es en realidad una versión más específica de una elipse.
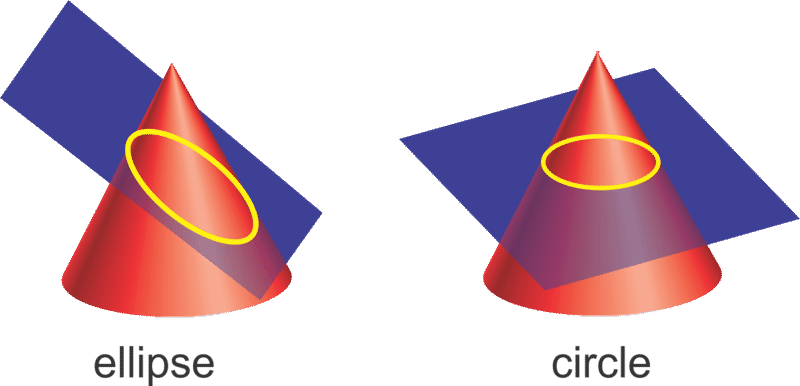
Por definición, una elipse es el conjunto de todos los puntos de tal manera que la suma de las distancias desde dos puntos fijos, llamados focos (el plural de foco), es constante.
Dibujar una elipse
Usaremos la definición de elipse para dibujar una elipse.
Paso 1: En una hoja de papel cuadriculado, dibuja un conjunto de ejes y traza (−2, 0) y (2, 0). Estos serán los focos.
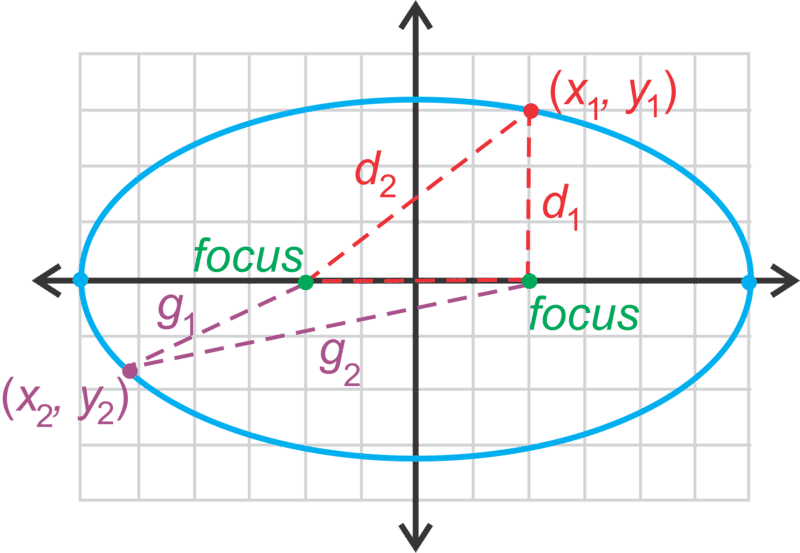
Paso 2: A partir de la definición, podemos concluir que un punto (x, y) está en una elipse si la suma de las distancias es siempre constante. En la imagen, d 1 + d 2 = r y g 1 + g 2 = r.
Paso 3: Determinar qué tan separados están los focos. Después, encuentra d 1 y d 2.
Paso 4: Determine si el punto (−2, 3) está en la elipse.
En este concepto, el centro de una elipse será (0,0). Una elipse puede tener una orientación vertical u horizontal (ver más abajo). Siempre hay dos focos y están en el eje mayor. El eje mayor es el más largo de los dos ejes que pasan por el centro de una elipse. También en el eje mayor están los vértices, que sus puntos finales y son los dos puntos más alejados uno del otro en una elipse. El eje más corto que pasa por el centro se denomina eje menor, con puntos finales llamados co-vértices. El punto medio de ambos ejes es el centro.
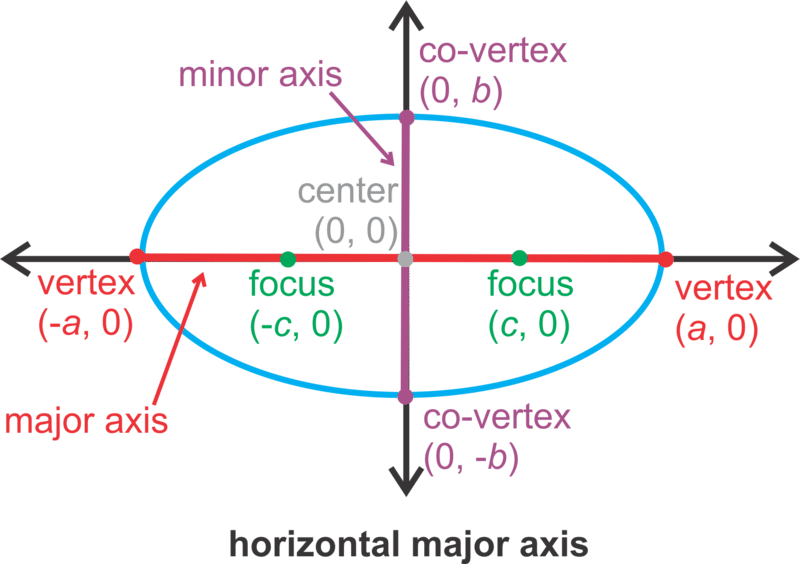
| \(\ \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\) |
HORIZONTAL eje mayor es el eje x con longitud 2a. eje menor es el eje y con longitud 2b. |
|---|---|
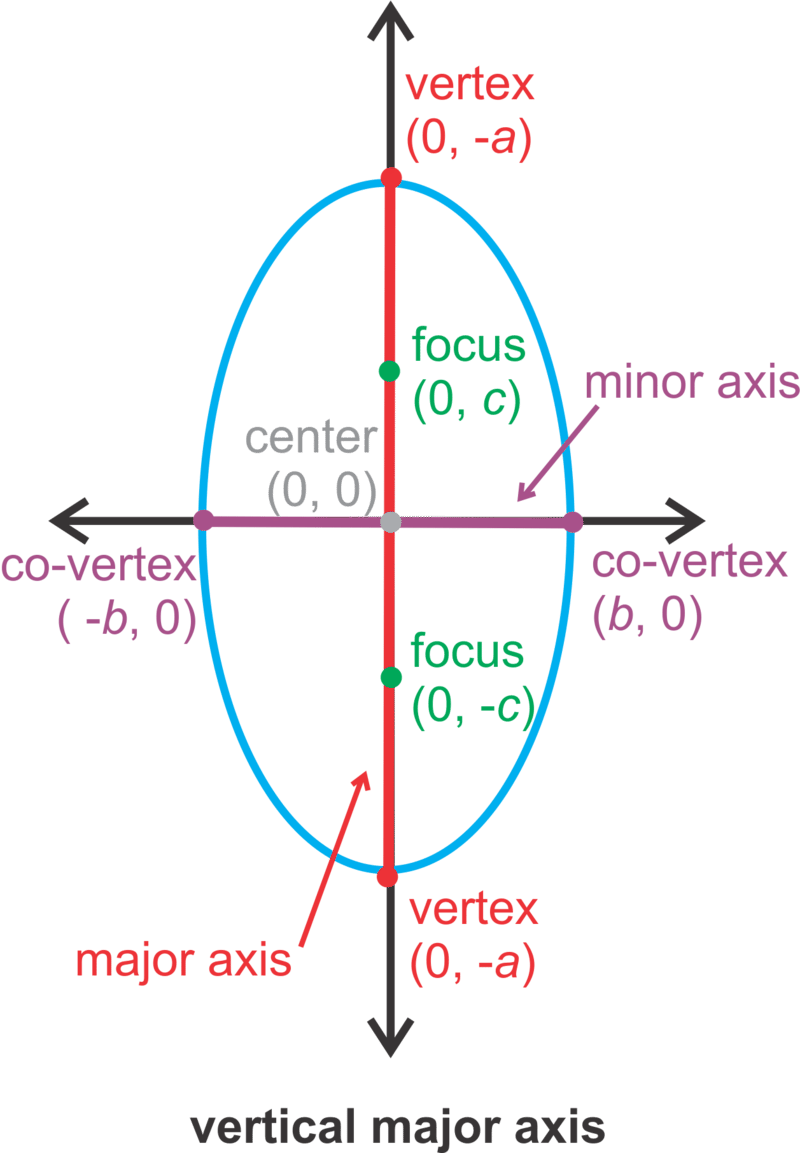
| \(\ \frac{x^{2}}{b^{2}}+\frac{y^{2}}{a^{2}}=1\) |
VERTICAL eje mayor es el eje y con longitud 2a. eje menor es el eje x con longitud 2b. |
Otros hechos importantes
- a es SIEMPRE mayor que b. Si son iguales, tenemos un círculo.
- Los focos, vértices y co-vértices se relacionan a través de una versión del Teorema de Pitágoras: c 2 = a 2 − b 2
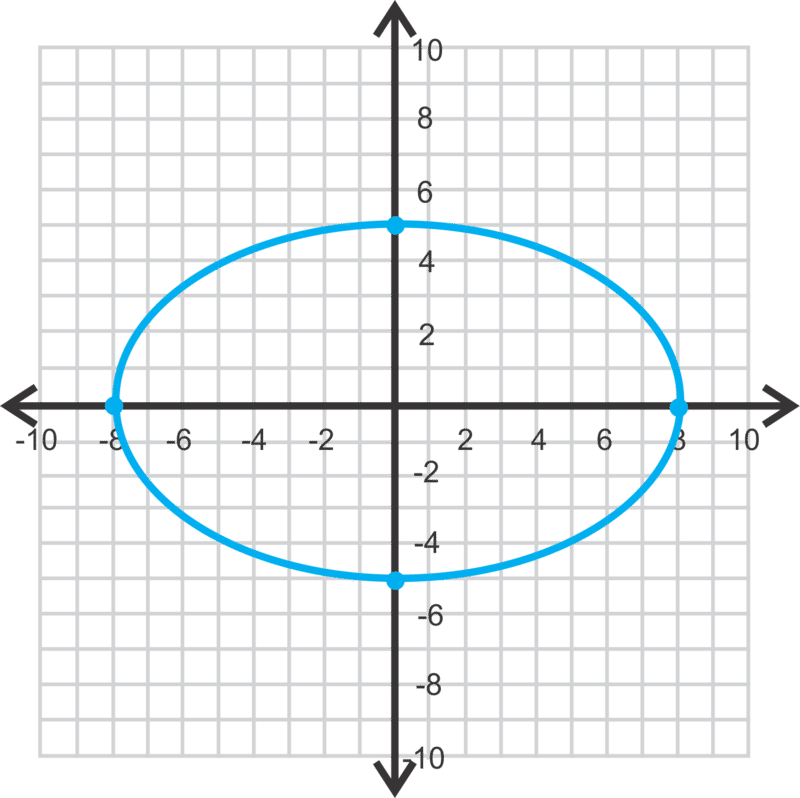
Vamos a encontrar los vértices, co-vértices y focos de\(\ \frac{x^{2}}{64}+\frac{y^{2}}{25}=1\). Entonces, graficemos la elipse.
Primero, necesitamos determinar si se trata de una elipse horizontal o vertical. Porque 64 > 25, sabemos que la elipse será horizontal. Por lo tanto,\(\ a^{2}=64\) haciendo\(\ a=\sqrt{64}=8\) y\(\ b^{2}=25\), haciendo\(\ b=\sqrt{25}=5\). Usando las imágenes de arriba, los vértices serán\(\ (8,0)\)\(\ (-8,0)\) y y los co-vértices serán\(\ (0,5)\) y\(\ (0,−5)\).
Para encontrar los focos, necesitamos usar la ecuación\(\ c^{2}=a^{2}-b^{2}\) y resolver para\(\ c\).
\ (\\ comenzar {alineado}
c^ {2} &=64-25=39\\
c &=\ sqrt {39}
\ end {alineado}\)
Los focos son\(\ (\sqrt{39}, 0)\) y\(\ (-\sqrt{39}, 0)\).
Para graficar la elipse, trazar los vértices y co-vértices y conectar los cuatro puntos para hacer la curva cerrada.
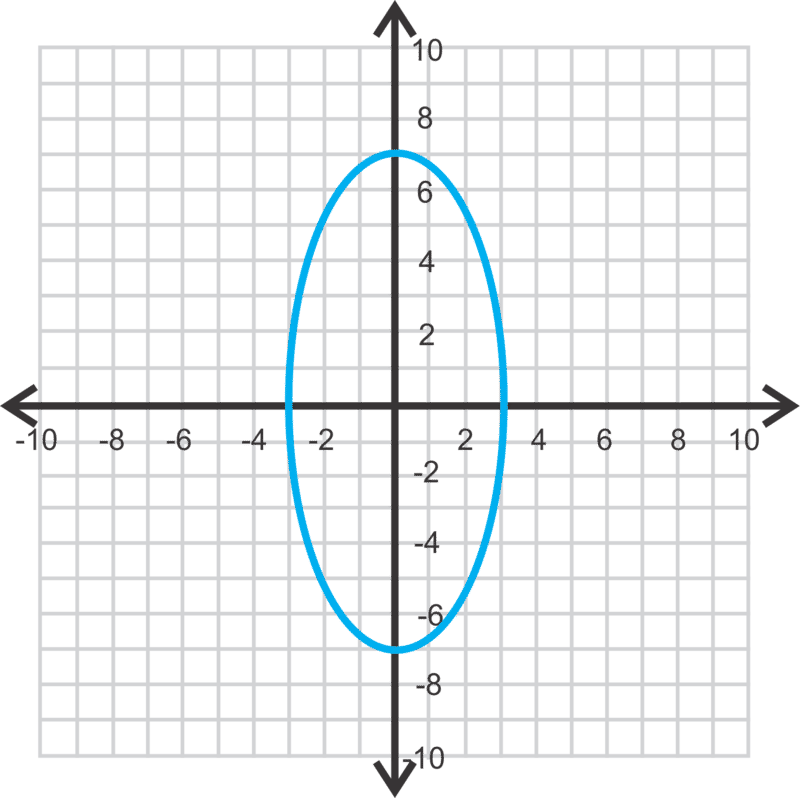
Ahora, graficemos\(\ 49 x^{2}+9 y^{2}=441\) e identifiquemos los focos.
Esta ecuación no está en forma estándar. Para reescribirlo en forma estándar, el lado derecho de la ecuación debe ser 1. Divide todo por 441.
\ (\\ comenzar {alineado}
\ frac {49 x^ {2}} {441} +\ frac {9 y^ {2}} {441} &=\ frac {441} {441}\
\ frac {x^ {2}} {9} +\ frac {y^ {2}} {49} &=1
\ end {alineado}\)
Ahora, podemos ver que se trata de una elipse vertical, dónde\(\ b=3\) y\(\ a=7\).
Para encontrar los focos, use\(\ c^{2}=a^{2}-b^{2}\).
\ (\\ begin {array} {c}
c^ {2} =49-9=40\\
c=\ sqrt {40} =2\ sqrt {10}
\ end {array}\)
Los focos son\(\ (0,2 \sqrt{10})\) y\(\ (0,-2 \sqrt{10})\).
Finalmente, escribamos ecuaciones para las elipses con las características dadas a continuación y centradas en el origen.
En cualquiera de las dos partes, es posible que desee dibujar la elipse para ayudar con la orientación.
- vértice: (−6, 0), covértice: (0, 4)
Podemos concluir que\(\ a=6\) y\(\ b=4\). La elipse es horizontal, porque el valor mayor\(\ a\),, es el valor x del vértice. La ecuación es\(\ \frac{x^{2}}{36}+\frac{y^{2}}{16}=1\).
- vértice: (0, 9), enfoque: (0, −5)
Eso lo sabemos\(\ a=9\) y\(\ c=5\) y que la elipse es vertical. Resolver para\(\ b\) usar\(\ c^{2}=a^{2}-b^{2}\)
\ (\\ begin {array} {l}
5^ {2} =9^ {2} -b^ {2}\\
25=81-b^ {2}\\
b^ {2} =56\ fila derecha b=2\ sqrt {14}
\ end {array}\)La ecuación es\(\ \frac{x^{2}}{56}+\frac{y^{2}}{81}=1\)
Ejemplos
Anteriormente, se le pidió que determinara dónde se ubicarían los focos de su gráfica.
Solución
Esta ecuación no está en forma estándar. Para reescribirlo en forma estándar, el lado derecho de la ecuación debe ser 1. Divide todo por 144.
\ (\\ comenzar {alineado}
\ frac {16 x^ {2}} {144} +\ frac {4 y^ {2}} {144} &=\ frac {144} {144}\
\ frac {x^ {2}} {9} +\ frac {y^ {2}} {36} &=1
\ end {alineado}\)
Ahora, podemos ver que se trata de una elipse vertical, dónde\(\ b=3\) y\(\ a=6\).
Para encontrar los focos, use\(\ c^{2}=a^{2}-b^{2}\).
\ (\\ comenzar {alineado}
c^ {2} &=36-9=27\\
c &=\ sqrt {27} =3\ sqrt {3}
\ end {alineado}\)
Los focos son por lo tanto\(\ (0,3 \sqrt{3})\) y\(\ (0,-3 \sqrt{3})\).
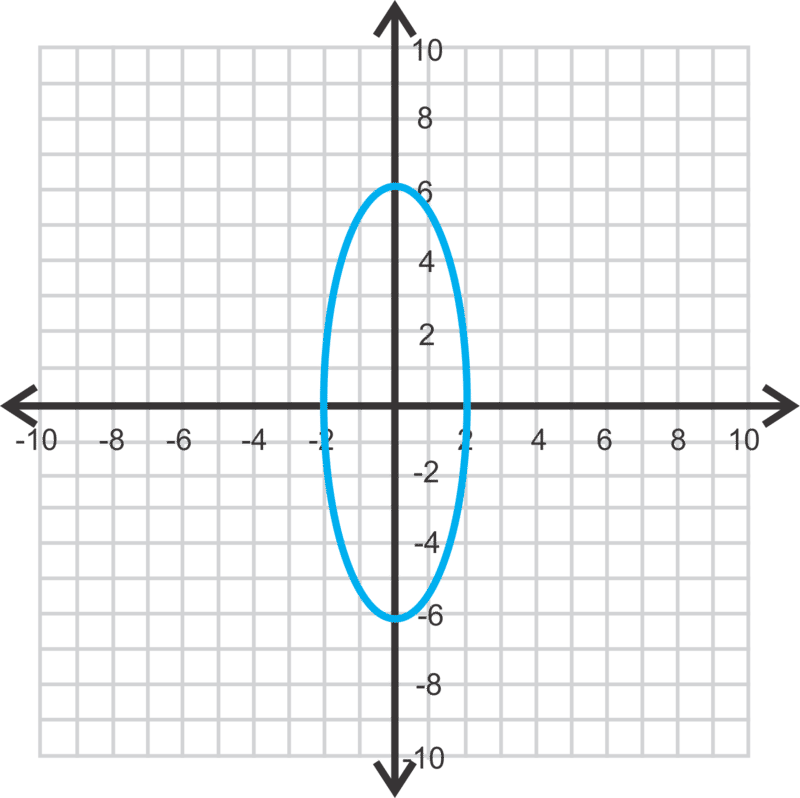
Encuentra los vértices, co-vértices, y focos de\(\ \frac{x^{2}}{4}+\frac{y^{2}}{36}=1\). Después, grafica la ecuación.
Solución
Debido a que el número mayor está por debajo\(\ y^{2}\), la elipse es vertical. Por lo tanto,\(\ a=6\) y\(\ b^{2}\). \(\ c^{2}=a^{2}-b^{2}\)Úselo para encontrar\(\ c\).
\ (\\ begin {array} {c}
c^ {2} =6^ {2} -2^ {2} =36-4=32\\
c=\ sqrt {32} =4\ sqrt {2}
\ end {array}\)
vértices:\(\ (0,6)\) y\(\ (0,−6)\)
co-vértices:\(\ (2,0)\) y\(\ (−2,0)\)
focos:\(\ (0,4 \sqrt{2})\) y\(\ (0,-4 \sqrt{2})\)
Grafica\(\ 49 x^{2}+64 y^{2}=3136\) y encuentra los focos.
Solución
Reescribir\(\ 49 x^{2}+64 y^{2}=3136\) en forma estándar.
\ (\\ comenzar {alineado}
\ frac {49 x^ {2}} {3136} +\ frac {64 y^ {2}} {3136} &=\ frac {3136} {3136}\
\ frac {x^ {2}} {64} +\ frac {y^ {2}} {49} &=1
\ end {alineado}\)
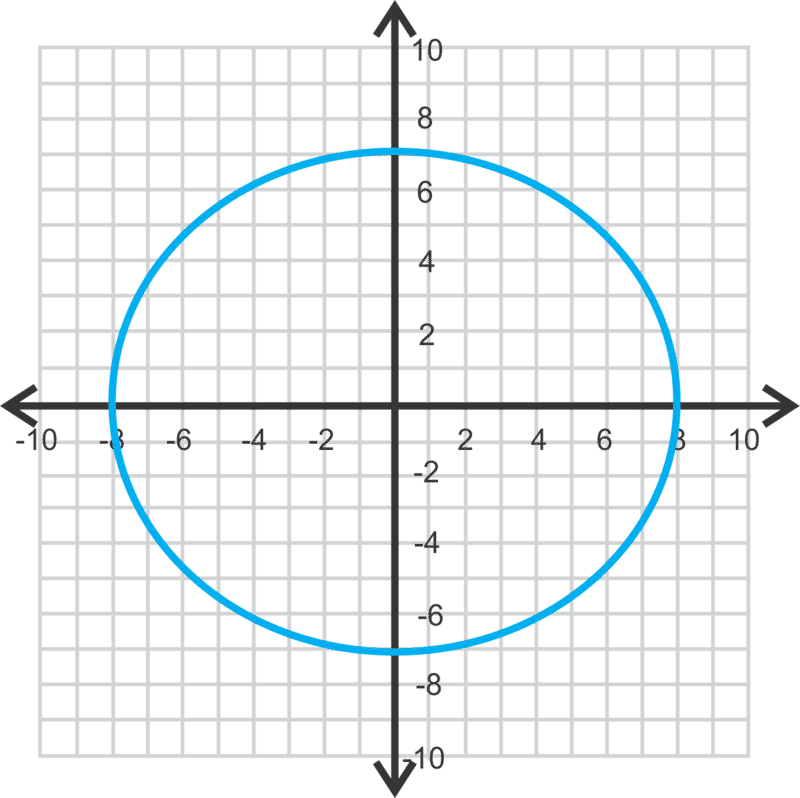
Esta elipse es horizontal con\(\ a=8\) y\(\ b=7\). Encuentra\(\ c\).
\ (\\ comenzar {alineado}
c^ {2} &=64-49=15\\
c &=\ sqrt {15}
\ end {alineado}\)
Los focos son\(\ (-\sqrt{15}, 0)\) y\(\ (\sqrt{15}, 0)\).
Encuentra la ecuación de la elipse con covértice\(\ (0,−7)\), enfoque\(\ (15,0)\) y centrado en el origen.
Solución
Porque el covértice es\(\ (0,−7)\),\(\ b=7\) y la elipse es horizontal. Por los focos, eso lo sabemos\(\ c=15\). Encuentra\(\ a\).
\ (\\ begin {aligned} 15^ {2} &=a^ {2} -7^ {2}\
a^ {2} &=225+49=274\ quad\ quad\ quad\ quad\ text {La ecuación es}\ frac {x^ {2}} {274} +\ frac {y^ {2}} {49} =1\\
a&=\ sqrt {274}\ end alineado}\)
Revisar
Encuentra los vértices, co-vértices y focos de cada elipse a continuación. Entonces, grafica.
- \(\ \frac{x^{2}}{9}+\frac{y^{2}}{16}=1\)
- \(\ 4 x^{2}+25 y^{2}=100\)
- \(\ \frac{x^{2}}{64}+y^{2}=1\)
- \(\ 81 x^{2}+100 y^{2}=8100\)
- \(\ \frac{x^{2}}{49}+\frac{y^{2}}{16}=1\)
- \(\ 121 x^{2}+9 y^{2}=1089\)
Encuentra la ecuación de la elipse, centrada en el origen, con la información dada.
- vértice: (−3, 0) co-vértice: (0, 1)
- co-vértice: (7, 0) eje mayor: 18 unidades
- vértice: (0, 5) eje menor: 4 unidades
- vértice: (0, 6) co-vértice: (−2, 0)
- co-vértice: (17, 0) enfoque: (0, 17)
- vértice: (4, 0) enfoque: (−3, 0)
- co-vértice: (−6, 0) enfoque: (0, 5)
- enfoque: (0, −9) eje menor: 16 unidades
- Aplicación de la vida real Una porción del patio trasero de la Casa Blanca se llama La elipse. El eje mayor es de 1058 pies y el eje menor es de 903 pies. Encuentra la ecuación de la elipse horizontal, asumiendo que está centrada en el origen.

Respuestas para problemas de revisión
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 10.5.
vocabulario
| Término | Definición |
|---|---|
| Ecuación de una elipse | Si el centro de una elipse es (0, 0), la ecuación de la elipse es de la forma\(\ \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\) o\(\ \frac{y^{2}}{a^{2}}+\frac{x^{2}}{b^{2}}=1\). |
| Eje Mayor | El eje mayor de una elipse es el diámetro más largo de la elipse. |
Atribuciones de imagen
- [Figura 1]
Crédito: Ad Meskens
Fuente: https://commons.wikimedia.org/wiki/File:Illu_pancrease.jpg; https://commons.wikimedia.org/wiki/File:President%27s_Park_with_White_House.jpg

