8.4.1: Área bajo la curva
- Page ID
- 108663
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Área bajo una curva
El cálculo del área bajo una línea recta se puede hacer con geometría. Calcular el área bajo una línea curva requiere cálculo. A menudo, el área bajo una curva se puede interpretar como la cantidad acumulada de lo que sea que la función esté modelando. Supongamos que la velocidad de un automóvil en metros por segundo puede ser modelada por una cuadrática durante los primeros 8 segundos de aceleración:
\(\ s(t)=t^{2}\)
¿Hasta dónde ha viajado el auto en 8 segundos?
Encontrar el área bajo una curva
El área bajo una curva se puede aproximar con rectángulos igualmente espaciados bajo una curva como se muestra a continuación. Para mayor consistencia, puede elegir si las cajas deben golpear la curva en la esquina izquierda, la esquina derecha, el valor máximo o el valor mínimo. Cuantas más cajas uses, más estrechas serán las cajas y así, más precisa será tu aproximación del área.
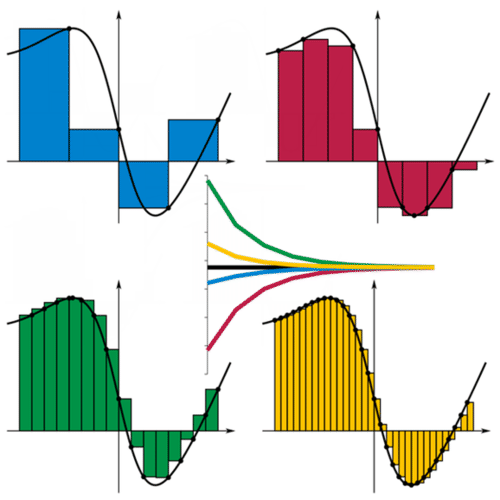
Los subintervalos se crean cuando un intervalo se divide en intervalos más pequeños y de igual tamaño. La aproximación azul utiliza cajas diestras para la altura de cada subintervalo. La aproximación roja asigna la altura de la caja para que sea el valor mínimo de la función en cada subintervalo. La aproximación verde asigna la altura de la caja para que sea el valor máximo de la función en cada subintervalo. La aproximación amarilla utiliza cajas para zurdos. Los rectángulos por encima del eje x tendrán área positiva y los rectángulos debajo del eje x tendrán área negativa en este contexto.
El uso de cajas para estimar el área bajo una curva se llama suma de Riemann. Toma la función\(\ f(x)=\frac{1}{2} x-2\). Para calcular la suma de Riemann (área bajo la curva) entre 1 y 9 de la función, primero dibuje la gráfica y las cajas.
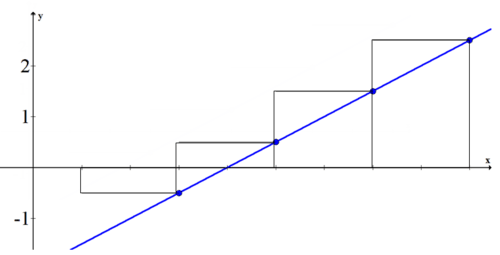
El área de la primera caja es 2 veces la altura de la función evaluada a 3:
\(\ 2 \cdot\left(\frac{1}{2} \cdot 3-2\right)=3-4=-1\)
Debido a que esta caja está debajo del eje x, su área es negativa.
El área para cada uno del resto de cajas es 2 veces la altura de la función evaluada a 5, 7 y 9.
\ (\\ begin {array} {l}
2\ cdot\ izquierda (\ frac {1} {2}\ cdot 5-2\ derecha) &=5-4=1\\
2\ cdot\ izquierda (\ frac {1} {2}\ cdot 7-2\ derecha) &=7-4=3\\
2\ cdot\ izquierda (\ frac {1} {2}\ cdot 9-2\ right) &=9-4=5
\ end {array}\)
La suma aproximada del área total bajo la curva es: −1+1+3+5=8 unidades cuadradas.
Las cuatro aproximaciones de área mostradas anteriormente mejoran a medida que aumenta el número de cajas. De hecho, el límite de cada aproximación a medida que el número de subintervalos (cajas) aumenta hasta el infinito es el área precisa bajo la curva.
Aquí es donde entra en juego la idea de cálculo de una integral. Una integral es el límite de una suma a medida que el número de summands aumenta hasta el infinito. Un summand es una de las muchas piezas que se suman.
\(\ \int f(x)=\lim _{n \rightarrow \infty} \sum_{i=1}^{n}(\text { Area of box } i)\)
El símbolo de la izquierda es el símbolo de cálculo de una integral.
Ejemplos
Anteriormente, se le pidió que determinara hasta dónde viaja un automóvil en 8 segundos.
Solución
Puedes usar el área bajo la curva para encontrar la distancia total recorrida en los primeros 8 segundos. Dado que la cuadrática es una curva debes elegir el número de subintervalos que deseas usar y si quieres cajas diestros o zurdos para estimar. Supongamos que elige 8 cajas para zurdos de ancho uno.
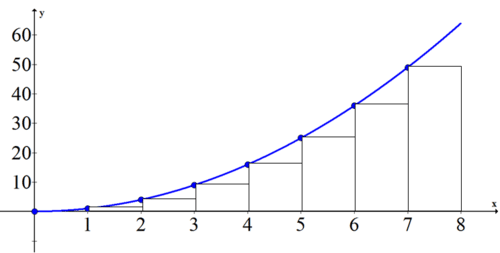
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Área de caja a la derecha | 10 | 11 | 14 | 19 | 116 | 125 | 136 | 149 |
La suma aproximada es 1+4+9+16+25+36+49=140. Esto significa que el auto viajó aproximadamente 140 metros en los primeros 8 segundos.
Evalúe el área exacta bajo la curva utilizada anteriormente,\(\ f(x)=\frac{1}{2} x-2\), usando la fórmula de área para un triángulo.
Solución
Recuerde que el área debajo del\(\ x\) eje es negativa mientras que el área por encima del\(\ x\) eje es positiva.
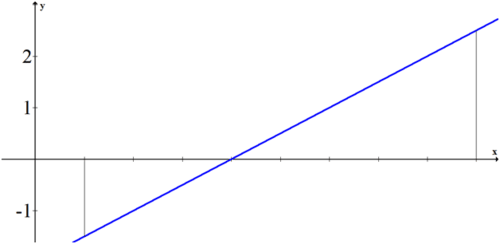
Área Negativa:\(\ \frac{1}{2} \cdot 3 \cdot 1.5=\frac{9}{4}\)
Área Positiva:\(\ \frac{1}{2} \cdot 5 \cdot 2.5=\frac{25}{4}\)
Área bajo la curva entre 1 y 8:\(\ \frac{25}{4}-\frac{9}{4}=\frac{16}{4}=4\)
Si compara esta respuesta con la aproximación anterior, parece que las aproximaciones que tienen 2 unidades de ancho producen un área con un error significativo.
Logan viaja en bicicleta a 20 mph durante 3 horas. Después se sube a un auto y conduce 60 mph durante 2 horas. Dibuje tanto el gráfico de distancia vs tiempo como el gráfico de tasa vs tiempo. Utilice un argumento de área bajo la curva para conectar las dos gráficas.
Solución
Distancia vs Tiempo:
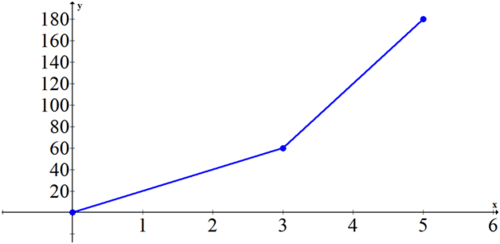
Tasa vs. tiempo:
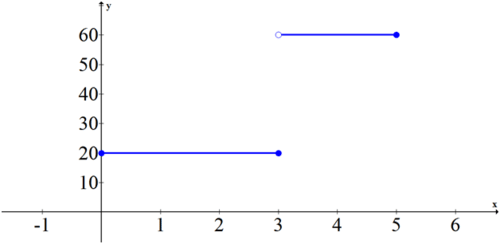
La pendiente de la primera gráfica es 20 de 0 a 3 y luego 60 de 3 a 5. La segunda gráfica es una gráfica de las pendientes de la primera gráfica. Si calculas el área de la segunda gráfica en los puntos clave 0, 1, 2, 3, 4 y 5 verás que se alinean perfectamente con los puntos de la primera gráfica.
| x | Área bajo curva de 0 a x |
| 0 | 0 |
| 1 | 20 |
| 2 | 40 |
| 3 | 60 |
| 4 | 120 |
| 5 | 180 |
Aproximar el área bajo la curva usando ocho subintervalos y puntos finales derechos.
\(\ f(x)=3 x^{2}-1,-1 \leq x \leq 7\)
Solución
Si bien una gráfica es útil para visualizar el problema y dibujar cada caja puede ayudar a dar sentido a cada summand, no siempre es necesario. Como van a haber 8 subintervalos sobre el intervalo total de −1≤x≤7, cada intervalo va a tener un ancho de 1. La altura de cada intervalo va a estar en los extremos de la derecha de cada subintervalo (0, 1, 2, 3, 4, 5, 6, 7).
\(\ \sum \text { height } \cdot \text { width }=\sum_{i=0}^{7}\left(3 i^{2}-1\right) \cdot 1=412\)
Aproximar el área bajo la curva usando veinte subintervalos y puntos finales izquierdos.
\(\ f(x)=x^{x}, 1 \leq x \leq 3\)
Solución
Cuando el número de subintervalos se hace grande y los subintervalos se vuelven extremadamente estrechos, será imposible dibujar una imagen precisa. Es por ello que es increíblemente importante usar la notación de suma y pensar a través de cuáles serán los índices y el argumento. Con 20 subintervalos entre [1,3], cada intervalo será de 0.1 de ancho. Puntos finales izquierdos significa que la primera caja tiene una altura de\(\ f(1)\) y la segunda caja tiene una altura de\(\ f(1.1)\).
\ (\\ comenzar {alineado}
\ suma\ texto {altura}\ cdot\ texto {ancho} &=f (1)\ cdot 0.1+f (1.1)\ cdot 0.1+f (1.2)\ cdot 0.1+\ cdots+f (2.9)\ cdot 0.1\\
&=0.1 (f (1) +f (1.1) +\ cdots f (2.9))\\
&=0.1\ cdot\ suma_ {i=10} ^ {29} f\ izquierda (\ frac {i} {10}\ derecha)\\
& =0.1\ cdot\ suma_ {i=10} ^ {29}\ izquierda (\ frac {i} {10}\ derecha) ^ {\ izquierda (\ frac {i} {10}\ derecha)}\\
&\ aprox 12.47144
\ final {alineado}\)
Tu calculadora puede calcular sumaciones cuando pasas por el menú de matemáticas.

Revisar
- Aproximar el área bajo la curva usando ocho subintervalos y puntos finales derechos.
\(\ f(x)=x^{2}-x+1,0 \leq x \leq 8\)
- Aproximar el área bajo la curva usando ocho subintervalos y puntos finales izquierdos.
\(\ f(x)=x^{2}-2 x+1,-4 \leq x \leq 4\)
- Aproximar el área bajo la curva usando veinte subintervalos y puntos finales izquierdos.
\(\ f(x)=\sqrt{x+3}, 0 \leq x \leq 4\)
- Aproximar el área bajo la curva usando 100 subintervalos y puntos finales izquierdos. Compare con su respuesta de #3.
\(\ f(x)=\sqrt{x+3}, 0 \leq x \leq 4\)
- Aproximar el área bajo la curva usando ocho subintervalos y puntos finales izquierdos.
\(\ f(x)=\cos (x), 0 \leq x \leq 4\)
- Aproximar el área bajo la curva usando veinte subintervalos y puntos finales izquierdos.
\(\ f(x)=\cos (x), 0 \leq x \leq 4\)
- Aproximar el área bajo la curva usando 100 subintervalos y puntos finales izquierdos.
\(\ f(x)=\cos (x), 0 \leq x \leq 4\)
La siguiente gráfica muestra la tarifa (en millas por hora) vs. tiempo (en horas) para un automóvil.
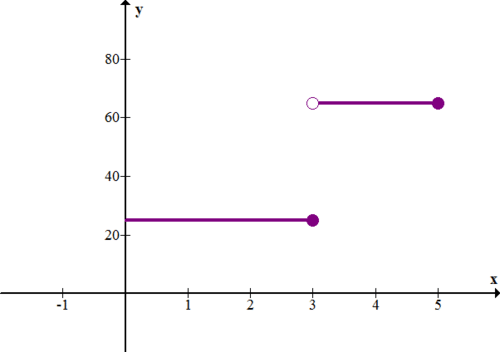
8. Describe lo que está pasando con el auto.
9. ¿Qué tan lejos viajó el auto en 5 horas?
La siguiente gráfica muestra la tasa (en pies por segundo) vs. tiempo (en segundos) para un automóvil.
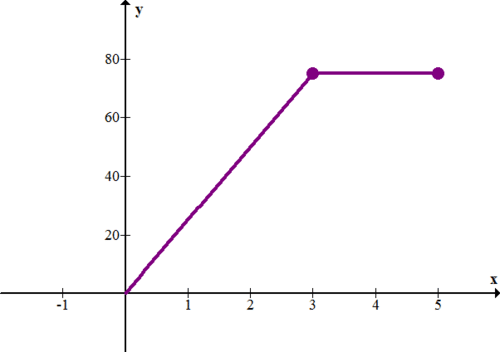
10. Describe lo que está pasando con el auto. En particular, ¿qué está pasando en los primeros 3 segundos?
11. ¿Qué tan lejos viajó el auto en 5 segundos?
La siguiente gráfica muestra la función\(\ f(x)=-(x-4)^{2}+16\), que representa la tasa (en pies por segundo) vs. tiempo (en segundos) para un corredor.
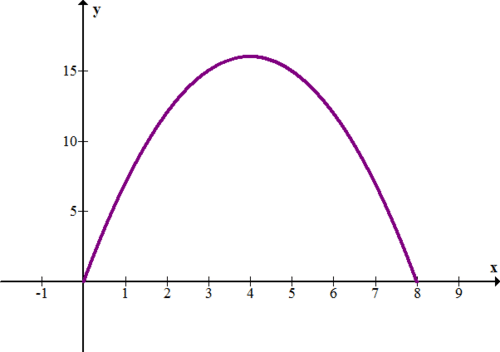
12. Describe lo que está pasando con el corredor. En particular, ¿qué sucede después de 4 segundos?
13. Usa rectángulos para aproximar la distancia total (en pies) que recorrió el corredor en los 8 segundos. Trate de obtener una aproximación lo más buena posible.
14. Explique cómo una integral es como lo contrario de un derivado.
15. ¿Cómo se relacionan las integrales con las sumas?
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 14.9.
El vocabulario
| Término | Definición |
|---|---|
| Δ | El símbolo “Δ”, leído “delta”, se utiliza para denotar “cambio en”, como en “el cambio en la velocidad a lo largo del tiempo”\(\ =\frac{\Delta v}{t}\). |
| integral definida | Una integral definida da el área entre el eje x y una curva en un intervalo definido. |
| límite | Un límite es el valor que la salida de una función se acerca a medida que la entrada de la función se acerca a un valor dado. |
| subintervalos | Los subintervalos se crean cuando un intervalo se divide en intervalos más pequeños de igual tamaño. |
| summand | Un summand es una expresión que se está sumando. Sigue directamente el símbolo sigma. |
Atribuciones de imagen
- [Figura 1]
Crédito: Fundación CK-12; KsMrQ
Fuente: https://commons.wikimedia.org/wiki/File:Riemann_sum_convergence.png
Licencia: CC BY-SA

