2.15: Pruebas- Pares Angulares y Segmentos
- Page ID
- 107388
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Ángulos verticales, bisectrices perpendiculares y otros teoremas basados en líneas de intersección o líneas paralelas y una transversal.
Teoremas sobre Líneas y Ángulos
Considera la línea\(l\) y un punto\(P\) que no está en línea\(l\). ¿Cuántas líneas existen que son paralelas\(l\) y pasan por el punto\(P\)?
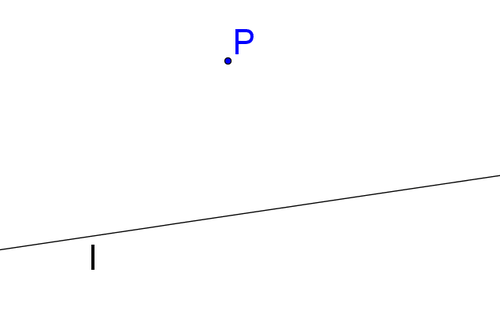
Teoremas de Línea y Ángulo
Considera dos líneas paralelas que están intersecadas por una tercera línea. (Recuerde que las marcas de verificación (≫) se pueden usar para indicar que dos líneas son paralelas).
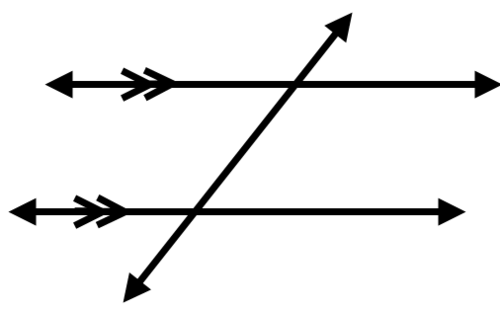
Esta tercera línea se llama transversal. Tenga en cuenta que se crean cuatro ángulos donde la transversal intersecta cada línea. Cada ángulo creado por la línea transversal y superior tiene un ángulo correspondiente con un ángulo creado por la línea transversal y la línea inferior. Estos pares de ángulos correspondientes se muestran codificados por colores a continuación. ¿Cómo crees que estos ángulos correspondientes están relacionados?

Su intuición y conocimiento de las traducciones podrían sugerir que estos ángulos son congruentes. Imagínese trasladar uno de los ángulos a lo largo de la transversal hasta que se encuentre con la segunda línea paralela. Coincidirá exactamente con su ángulo correspondiente. Esto se conoce como el postulado de ángulo correspondiente:
Si dos líneas paralelas son cortadas por una transversal, entonces los ángulos correspondientes son congruentes.
Recuerda que un postulado es una afirmación que se acepta como verdadera sin pruebas. Tu conocimiento de las traducciones debería convencerte de que este postulado es cierto.
Recursos
Echemos un vistazo a algunos problemas de ejemplo.
1. Recordemos que los ángulos verticales son un par de ángulos opuestos creados por líneas que se cruzan. Demostrar que los ángulos verticales son congruentes.
Para esta prueba, no se le da una imagen específica. Cuando no se le da una imagen, ayuda a crear una imagen genérica para hacer referencia en su prueba. Es importante que la imagen no incluya ninguna información que no puedas asumir. A continuación se muestra una imagen genérica de líneas que se cruzan con ángulos numerados para referencia.
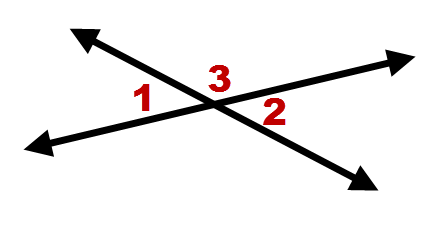
En esta imagen,\(\angle 1\) y\(\angle 2\) son ángulos verticales. Tu trabajo es demostrarlo\(\angle 1\cong \angle 2\). Puedes usar cualquier estilo de prueba que prefieras. Aquí hay una prueba de dos columnas.
|
Declaraciones |
Razones |
|
\(m\angle 1+m\angle 3=180^{\circ}\)y\(m\angle 2+m\angle 3=180^{\circ}\) |
Dos ángulos que forman una línea son complementarios |
| \(m\angle 1+m\angle 3=m\angle 2+m\angle 3\) |
Sustitución algebraica |
| \(m\angle 1=m\angle 2\) |
Resta propiedad de igualdad |
| \(\angle 1\cong \angle 2\) |
Si dos ángulos tienen la misma medida, son congruentes. |
Los ángulos verticales son congruentes es un teorema. Ahora que se ha probado, se puede utilizar en futuras pruebas sin volver a probarlo.
2. Cuando dos líneas paralelas son cortadas por una transversal, se forman dos pares de ángulos interiores alternos. En el diagrama de abajo,\(\angle 3\) y\(\angle 5\) se alternan los ángulos interiores. Del mismo modo,\(\angle 4\) y\(\angle 6\) son ángulos interiores alternos.
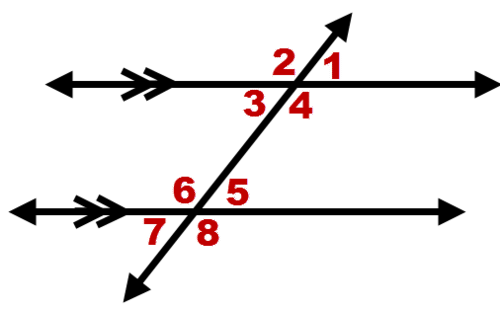
Demostrar que si dos líneas paralelas son cortadas por una transversal, los ángulos interiores alternos son congruentes.
Usa el diagrama anterior y demuéstralo\(\angle 3\cong \angle 5\). (La misma prueba exacta lo demostraría\(\angle 4\cong \angle 6\)). Nuevamente, en general puedes usar cualquier estilo de prueba que prefieras. Aquí hay una prueba de párrafo.
\(\angle 1\cong \angle 3\)porque son ángulos verticales y los ángulos verticales son siempre congruentes. \(\angle 1\cong \angle 5\)porque son ángulos correspondientes creados por líneas paralelas y los ángulos correspondientes son congruentes cuando las líneas son paralelas. \(\angle 3\cong \angle 5\)porque si dos ángulos son congruentes con el mismo ángulo, son congruentes entre sí por la propiedad transitiva .
*Nota: La propiedad transitiva establece que si dos objetos son iguales/congruentes al mismo tercer objeto, entonces son iguales/congruentes entre sí. La propiedad transitiva es una forma de sustitución. Se puede utilizar en cualquier comprobante.
3. La afirmación “si dos líneas paralelas son cortadas por una transversal, entonces los ángulos interiores alternos son congruentes” es un teorema . Ahora que se ha probado, se puede utilizar en futuras pruebas sin volver a probarlo.
Demostrar que los puntos en la bisectriz perpendicular de un segmento de línea son equidistantes de los puntos finales del segmento de línea.
Comience explorando esta afirmación. Dibuja una imagen de un segmento de línea y una bisectriz perpendicular de este segmento. Recuerde que una bisectriz perpendicular es perpendicular al segmento de línea (lo encuentra en ángulo recto) y bisecciona el segmento de línea (lo corta por la mitad).
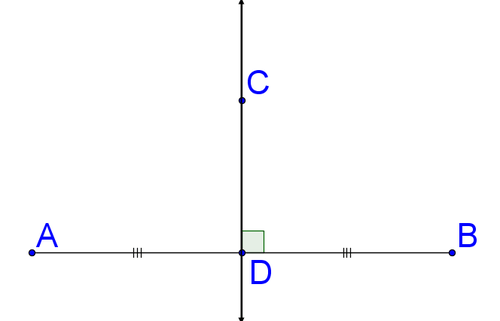
El reclamo es que cualquier punto en la bisectriz perpendicular (como el punto\(C\)), está a la misma distancia de cada punto final. Es decir, la afirmación es que para algún punto genérico\(C\) sobre la bisectriz perpendicular,\(\overline{AC}\cong \overline{BC}\).
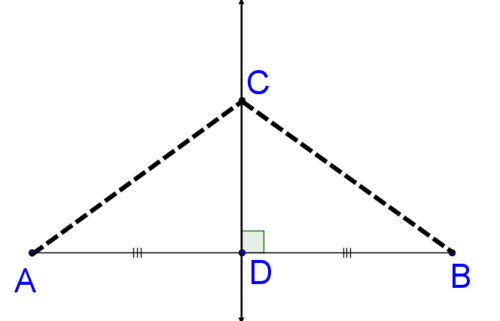
Para probar la afirmación original, bastará con probar que si\(\overleftrightarrow{CD}\) es la bisectriz perpendicular a\(\overline{AB}\) con\(D\) on\(\overline{AB}\), entonces\(\overline{AC}\cong \overline{BC}\) usando el diagrama anterior como referencia. Recuerda, en general puedes usar cualquier estilo de prueba que prefieras. Aquí hay un diagrama de flujo. Para probar esta afirmación, demostrará que los dos triángulos son congruentes y luego que los\(\overline{AC}\) y\(\overline{BC}\) son correspondientes partes por lo que deben ser congruentes.
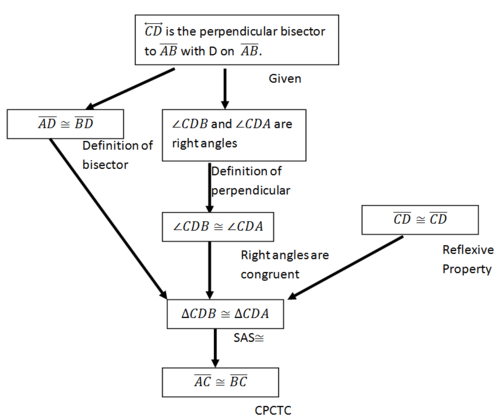
La declaración “los puntos en una bisectriz perpendicular de un segmento de línea son equidistantes de los puntos finales del segmento” es un teorema. Ahora que se ha probado, se puede utilizar en futuras pruebas sin volver a probarlo.
Ejemplo\(\PageIndex{1}\)
Anteriormente, se le preguntó cuántas líneas existen que son paralelas a l y pasan por punto\(P\).

Solución
El sentido común debería decirte que solo hay una línea a través de la\(P\) que es paralela a\(l\).
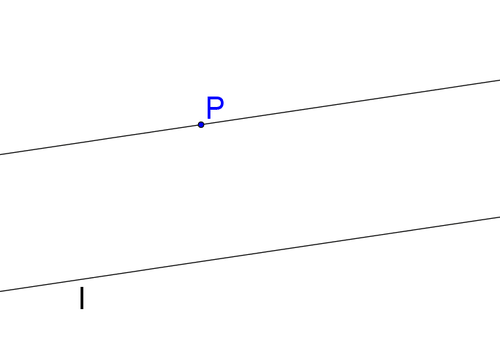
Curiosamente, desde hace cientos de años la gente ha intentado probar esta afirmación a partir de declaraciones más simples sin suerte. Finalmente, se aceptó que simplemente debía ser un postulado, una afirmación que se supone que es verdadera sin pruebas. Esto se conoce como el postulado paralelo.
Ejemplo\(\PageIndex{2}\)
Si los ángulos correspondientes son congruentes, ¿entonces las líneas son paralelas?
Solución
Esto se conoce como el inverso del postulado de ángulos correspondientes. El postulado original decía:
Original: Si las líneas son paralelas, entonces los ángulos correspondientes son congruentes.
Aquí, la parte “si” de la declaración (conocida como la hipótesis) se cambia con la parte “entonces” de la declaración (conocida como la conclusión).
Converse: Si los ángulos correspondientes son congruentes, entonces las líneas son paralelas.
En general, el hecho de que una afirmación sea cierta no significa necesariamente que su contrario sea cierto. En este caso, lo contrario sí resulta ser cierto. La única manera de que los ángulos correspondientes sean congruentes es que las líneas sean paralelas. Los ángulos correspondientes converse también es un postulado, lo que significa que es aceptado como verdadero sin pruebas.
Ejemplo\(\PageIndex{3}\)
Demostrar que si las líneas son paralelas, entonces los ángulos interiores del mismo lado (como\(\angle 3\) y\(\angle 6\)) son complementarios.
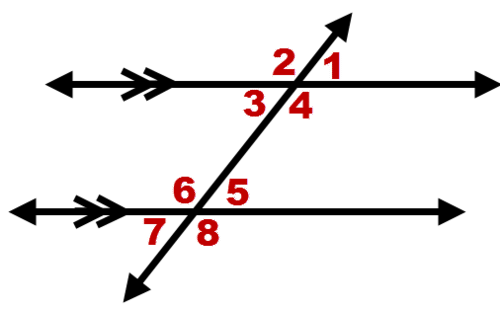
Solución
En general puedes usar cualquier estilo de prueba que prefieras. Aquí, usa una prueba de párrafo.
\(\angle 3\cong \angle 5\)porque son ángulos interiores alternativos creados por líneas paralelas y ángulos interiores alternativos son congruentes cuando las líneas son paralelas. \(m\angle 3=m\angle 5\)porque los ángulos congruentes tienen la misma medida. \(m\angle 5+m\angle 6=180^{\circ}\)porque dos ángulos que forman una línea son suplementarios. Por sustitución ,\(m\angle 3+m\angle 6=180^{\circ}\) . \(\angle 3\)y\(\angle 6\) son complementarios porque dos ángulos con medidas que se suman a\(180^{\circ}\) son complementarios.
La afirmación “si dos líneas paralelas son cortadas por una transversal, entonces los ángulos interiores del mismo lado son suplementarios” es un teorema . Ahora que se ha probado, se puede utilizar en futuras pruebas sin volver a probarlo.
Ejemplo\(\PageIndex{4}\)
Demostrar que si los ángulos interiores alternos son congruentes, entonces las líneas son paralelas.
Solución
Esto es lo contrario del teorema de ángulos interiores alternos.
Original: Si las líneas son paralelas, entonces los ángulos interiores alternos son congruentes.
Aquí, la parte “si” de la declaración (conocida como la hipótesis) se cambia con la parte “entonces” de la declaración (conocida como la conclusión).
Converse: Si los ángulos interiores alternos son congruentes, entonces las líneas son paralelas.
Para probar esta afirmación, comience con una imagen de ángulos interiores alternos que se supone que son congruentes, pero no asuma que las líneas son paralelas. En la imagen de abajo, asuma\(\angle 1\cong \angle 2\). Demostrar eso\(m \parallel n\) (dos barras paralelas indican líneas paralelas).
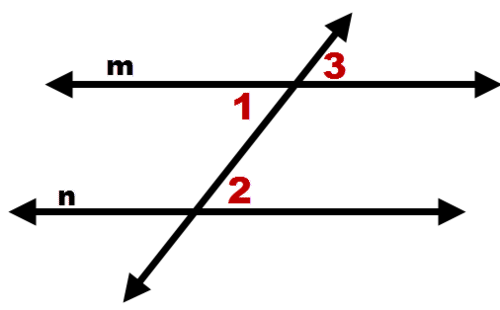
|
Declaraciones |
Razones |
| \(\angle 1\cong \angle 2\) |
Dado |
| \(\angle 1\cong \angle 3\) |
Los ángulos verticales son congruentes |
| \(\angle 2\cong \angle 3\) |
Propiedad transitiva de congruencia |
| \(m \parallel n\) |
Si los ángulos correspondientes son congruentes entonces las líneas son paralelas. |
Revisar
1. En el problema 1 de la sección anterior de Teoremas de Línea y Ángulo, se probó el teorema “los ángulos verticales son congruentes” con una prueba de dos columnas. Reescribir esta prueba en formato de párrafo.
2. En el problema 2 de la sección anterior de Teoremas de Línea y Ángulo, se probó con una prueba de párrafo el teorema “si las líneas son paralelas entonces los ángulos interiores alternos son congruentes”. Reescribe esta prueba con un diagrama de flujo.
3. En el problema 3 de la sección anterior de Teoremas de Línea y Ángulo, se probó el teorema “los puntos en una bisectriz perpendicular de un segmento lineal son equidistantes de los puntos finales del segmento” con un diagrama de flujo. Vuelva a escribir esta prueba en un formato de dos columnas.
4. En el Ejemplo 3, se probó con una prueba de párrafo el teorema “si las líneas son paralelas entonces los ángulos interiores del mismo lado son suplementarios”. Vuelva a escribir esta prueba en un formato de dos columnas.
5. En el Ejemplo 4, se probó con una prueba de dos columnas el teorema “si los ángulos interiores alternos son congruentes entonces las líneas son paralelas”. Reescribe esta prueba con un diagrama de flujo.
6. Los ángulos exteriores alternativos están fuera de un par de líneas y en lados opuestos de una transversal. \(\angle 2\)y\(\angle 8\) son un ejemplo de ángulos exteriores alternos. \ ángulo 1 y\ ángulo 7 son otro ejemplo de ángulos exteriores alternos.
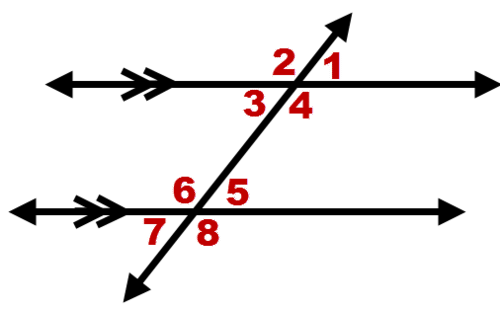
El teorema “si las líneas son paralelas entonces los ángulos exteriores alternos son congruentes” se demuestra parcialmente a continuación. Rellene los espacios en blanco para completar la prueba. Tenga en cuenta que los ángulos referenciados son de la imagen de arriba.
|
Declaraciones |
Razones |
|
Dos líneas paralelas son cortadas por una transversal |
_________ |
| \(\angle 2\cong \angle 6\) |
_________ |
| \(\angle 6\cong \underline{\qquad}\) |
Los ángulos verticales son congruentes. |
| _________ |
Propiedad transitiva. |
7. ¿Qué es lo contrario del teorema “si las líneas son paralelas, entonces los ángulos interiores del mismo lado son complementarios”?
8. Demuestra lo contrario que escribiste en #7. Usa cualquier estilo de prueba que prefieras.
9. En el problema 3 de la sección anterior de Teoremas de Línea y Ángulo, se probó el teorema “los puntos en una bisectriz perpendicular de un segmento de línea son equidistantes de los puntos finales del segmento”. Este teorema podría reescribirse como “si un punto está en la bisectriz perpendicular de un segmento de línea, entonces el punto es equidistante de los puntos finales del segmento de línea”. ¿Cuál es lo contrario de este teorema? Para verificar tu respuesta, mira #10.
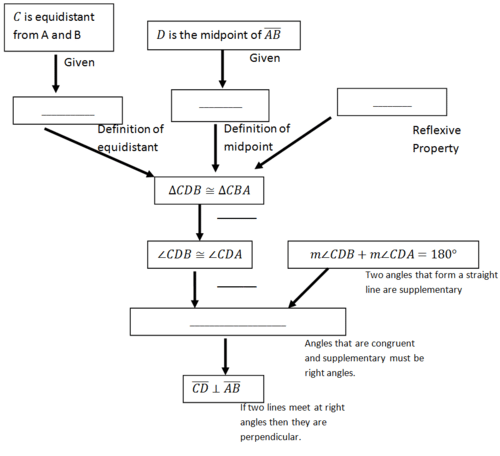
10. Lo contrario del teorema en #9 es “si un punto es equidistante de los puntos finales de un segmento de línea, entonces el punto está en la bisectriz perpendicular del segmento de línea”. Para probar este nuevo teorema puedes usar la imagen de abajo.
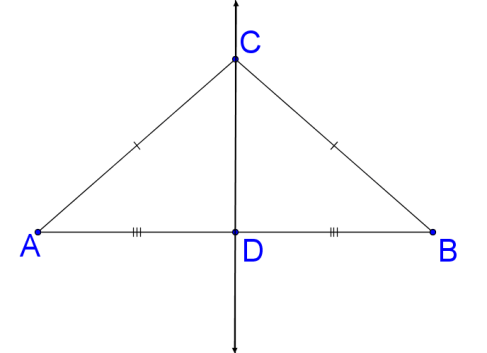
Supongamos que\(C\) el punto es un punto aleatorio que es equidistante de los puntos finales\(A\) y\(B\). Punto\(D\) es el punto medio del segmento de línea\(\overline{AB}\). Tu objetivo es demostrar que\(\overline{CD}\) debe ser perpendicular a\(\overline{AB}\) (\(\overline{CD}\perp \overline{AB}\)). Este nuevo teorema se demuestra parcialmente a continuación. Rellene los espacios en blanco para completar la prueba.
En 11-13, demostrarás que si dos ángulos son complementarios al mismo ángulo, entonces los dos ángulos son congruentes.
11. Dibuja una imagen genérica de esta situación y etiquete los tres ángulos.
12. ¿Cuáles son los “dados” de tu foto? ¿Qué intentas probar?
13. Escribe una prueba de la declaración usando el estilo de prueba que prefieras.
14. Usando tu trabajo del 11-13 para ayudar, demuestra que si dos ángulos son complementarios al mismo ángulo, entonces los dos ángulos son congruentes.
15. Dar al menos 3 métodos para probar que las líneas son paralelas.
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 4.2.
El vocabulario
| Término | Definición |
|---|---|
| ángulos interiores alternos | Los ángulos interiores alternos son dos ángulos que se encuentran en el interior de dos líneas diferentes, pero en los lados opuestos de la transversal. |
| Ángulos correspondientes | Los ángulos correspondientes son dos ángulos que están en la misma posición con respecto a la transversal, pero en líneas diferentes. |
| bisectriz perpendicular | Una bisectriz perpendicular de un segmento de línea pasa a través del punto medio del segmento de línea e intersecta el segmento de línea en\(90^{\circ}\). |
| postular | Un postulado es una afirmación que se acepta como verdadera sin pruebas. |
| transversal | Una transversal es una línea que cruza otras dos líneas. |
Recursos adicionales
Elemento Interactivo

