1.2:1.2 Transformaciones gráficas
- Page ID
- 107333
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Las funciones básicas son poderosas, pero son extremadamente limitadas hasta que puedes cambiarlas para que coincidan con cualquier situación dada. Transformación significa que puede cambiar la ecuación de una función básica sumando, restando y/o multiplicando por constantes y así provocar un cambio correspondiente en la gráfica. ¿Cuáles son los efectos de las siguientes transformaciones?
1. \(f(x) \rightarrow f(x+3)\)
2. \(h(x) \rightarrow h(x)-5\)
3. \(g(x) \rightarrow-g(2 x)\)
4. \(j(x) \rightarrow j\left(-\frac{x}{2}\right)\)
Funciones Transformadoras
Una función es una regla que toma cualquier entrada\(x\) y da una salida específica. Cuando usas letras como\(f\),,\(g\)\(h\), o\(j\) para describir la regla, esto se llama notación de función. Para interpretar qué efecto tendrá el cambio algebraico en la ecuación sobre la gráfica, es importante poder leer esos cambios en la notación general de funciones y luego aplicarlos a casos específicos.
Al transformar una función, se puede transformar el argumento (la parte dentro de los paréntesis con el\(x\)), o la función misma. Hay dos formas de transformar linealmente el argumento. Puede multiplicar el\(x\) por una constante y/o agregar una constante a la\(x\) como se muestra a continuación:
\(f(x) \rightarrow f(b x+c)\)
La función en sí también se puede transformar linealmente de la misma manera:
\(f(x) \rightarrow a f(x)+d\)
Cada una de las letras\(a\)\(b\),\(c\),, y\(d\) corresponde a un cambio muy específico. Algunos de estos cambios son sencillos, mientras que otros pueden ser lo contrario de lo que podrías esperar.
- \(a\)es un estiramiento vertical. Si\(a\) es negativo, también hay una reflexión a través del\(x\) eje.
- \(d\)es un desplazamiento vertical. Si\(d\) es positivo, entonces el turno es hacia arriba. Si\(d\) es negativo, entonces el turno es a la baja.
Al transformar el argumento de la función las cosas son más complicadas.
- \(\frac{1}{b}\)es un estiramiento horizontal. Si\(b\) es negativo, también hay una reflexión a través del\(y\) eje.
- \(c\)es un desplazamiento horizontal. Si\(c\) es positivo, entonces el turno es hacia la izquierda. Si\(c\) es negativo, entonces el turno es hacia la derecha. Observe que esto es lo contrario de lo que la mayoría de la gente piensa al principio.
La parte más complicada de transformar el argumento de una función es el orden en el que se llevan a cabo las transformaciones. Muchas veces tiene sentido aplicar la transformación a una función específica que se conoce y luego describir la transformación que se ve.
La gráfica siguiente muestra la transformación\(f(x) \rightarrow f(3 x-6)\) aplicada a una parábola simple:
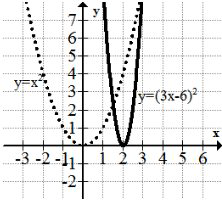
Claramente la gráfica es más estrecha y a la derecha, pero para ser específico hay que mirar más de cerca. Primero, observe que la transformación está enteramente dentro del argumento de la función. Esto afecta sólo a los valores horizontales. Esto significa que mientras la gráfica parece estar estirada verticalmente, debes mantener tu perspectiva enfocada en una compresión horizontal.
Mira cuidadosamente el vértice de la parábola. Se ha trasladado a la derecha dos unidades. Esto se debe a que primero toda la gráfica se desplazó completamente hacia la derecha 6 unidades. Entonces la función se comprimió horizontalmente por un factor de 3 lo que significa que el punto (6, 0) se convirtió en (2, 0) y el\(x\) valor de cada otro punto también se comprimió por un factor de 3 hacia la línea\(x=0\). Este método es contra-intuitivo porque requiere leer las transformaciones hacia atrás (lo opuesto a la forma en que el orden de las operaciones te dice).
Alternativamente, el argumento puede ser factorizado y cada componente de la transformación se presentará.
\(f(3(x-2))\)
Esta vez el estiramiento ocurre desde el centro de la gráfica transformada, no desde el origen. Este método es en última instancia el método preferido.
De cualquier manera, esta es una compresión horizontal por un factor de 3 y un desplazamiento horizontal hacia la derecha en 2 unidades.
Ahora toma la transformación\(f(x) \rightarrow-\frac{1}{4} f(x)+3 .\) Se describe un estiramiento vertical por un factor de\(\frac{1}{4},\) una reflexión sobre el\(x\) eje, y un desplazamiento vertical 3 unidades hacia arriba. A diferencia de lo que vio anteriormente, el orden de las transformaciones para cualquier cosa fuera del argumento es directamente lo que dicta el orden de las operaciones.
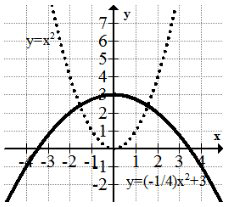
Primero, la parábola se refleja sobre el\(x\) eje y se comprime verticalmente para que aparezca más ancha. Entonces, cada punto se mueve hacia arriba 3 unidades.
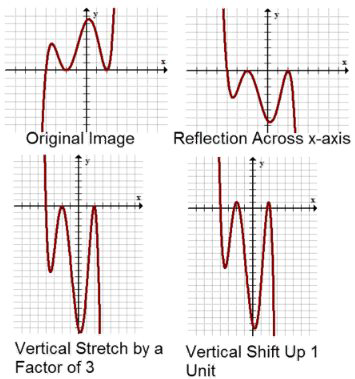
La transformación\(f(x) \rightarrow-3 f\left(-\frac{1}{2} x-1\right)+1\) contiene todas las transformaciones posibles. Los componentes horizontal y vertical no interactúan entre sí y por lo tanto su descripción de la transformación puede comenzar con cualquiera de los componentes. Aquí, comience por describir los componentes verticales de la transformación:
Primero, hay reflexión a través del\(x\) eje y un estiramiento vertical por un factor de 3. Después, hay un desplazamiento vertical hacia arriba 1 unidad. A continuación se muestra una imagen de una función no específica pasando por las transformaciones verticales.
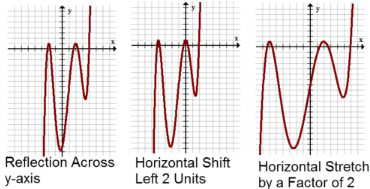
Para averiguar los componentes horizontales de la transformación, comience factorizando el interior de los paréntesis (el argumento):
\(f\left(-\frac{1}{2} x-1\right)=f\left(-\frac{1}{2}(x+2)\right)\)
Factorización revela una reflexión a través del\(y\) eje, un desplazamiento horizontal a la izquierda 2 unidades y un estiramiento horizontal por un factor de\(2 .\) Abajo es una imagen de la misma función pasando por las transformaciones horizontales.
Ejemplos
Anteriormente, se le dio un problema sobre los efectos de las siguientes transformaciones:
\(f(x) \rightarrow f(x+3)\)
Esta transformación desplaza toda la gráfica a la izquierda 3 unidades. Un error común es cambiar a la derecha porque los tres son positivos.
\(h(x) \rightarrow h(x)-5\)
Esta transformación desplaza la gráfica completa hacia abajo 5 unidades.
\(g(x) \rightarrow-g(2 x)\)
Esta transformación es una reflexión vertical a través del eje x y una compresión horizontal por un factor de 2.
\(j(x)=j\left(-\frac{x}{2}\right)\)
Esta transformación es una reflexión horizontal a través del\(y\) eje y un estiramiento horizontal por un factor de\(2 .\) Un error común es ver el\(\frac{1}{2}\) y creer que los\(x\) valores serán la mitad de grandes que es una compresión horizontal. Sin embargo, los valores\ x\) deben ser dos veces más grandes para contrarrestar este factor de\(\frac{1}{2}\)
Describa la siguiente transformación en palabras:\(g(x) \rightarrow 2 g(-x)\)
Estiramiento vertical por un factor de 2 y una reflexión a través del\(y\) eje.
Describa la transformación que cambiaría\(h(x)\) de las siguientes maneras:
- Compresión vertical por un factor de 3.
- Desplazamiento vertical hacia abajo 4 unidades.
- Desplazamiento horizontal a la derecha 5 unidades.
\(\frac{1}{3} h(x-5)-4\)
Describa la transformación que cambiaría\(f(x)\) de las siguientes maneras:
- Estiramiento horizontal por un factor de 4 y un desplazamiento horizontal de 3 unidades hacia la derecha.
- Reflexión vertical a través del\(x\) eje y un desplazamiento hacia abajo 2 unidades.
\(-f\left(\frac{1}{4}(x-3)\right)-2\)o\(-f\left(\frac{1}{4} x-\frac{3}{4}\right)-2\)
Revisar
Describir las siguientes transformaciones en palabras.
1. \(g(x) \rightarrow-g(-x)\)
2. \(f(x) \rightarrow-f(x+3)\)
3. \(h(x) \rightarrow h(x+1)-2\)
4. \(j(x) \rightarrow j(-x+3)\)
5. \(k(x) \rightarrow-k(2 x)\)
6. \(f(x) \rightarrow 4 f\left(\frac{1}{2} x+1\right)\)
7. \(g(x) \rightarrow-3 g(x-2)-2\)
8. \(h(x) \rightarrow 5 h(x+1)\)
9. Describa la transformación que cambiaría\(h(x)\) de las siguientes
maneras:
- Estiramiento vertical por un factor de 2
- Desplazamiento vertical hacia arriba 3 unidades.
- Desplazamiento horizontal a la derecha 2 unidades.
10. Describa la transformación que cambiaría\(f(x)\) de las siguientes
maneras:
- Reflexión vertical a través del eje x.
- Desplazamiento vertical hacia abajo 1 unidad.
- Desplazamiento horizontal a la izquierda 2 unidades.
11. Describa la transformación que cambiaría\(g(x)\) de las siguientes
maneras:
- Compresión vertical por un factor de 4.
- Reflexión a través del\(y\) eje.
12. Describa la transformación que cambiaría\(j(x)\) de las siguientes
maneras:
- Compresión horizontal por un factor de 3.
- Desplazamiento vertical hacia arriba 3 unidades.
- Desplazamiento horizontal a la derecha 2 unidades.
13. Describa la transformación que cambiaría\(k(x)\) de las siguientes
maneras:
- Estiramiento horizontal por un factor de 4.
- Desplazamiento vertical hacia arriba 3 unidades.
- Desplazamiento horizontal a la izquierda 1 unidad.
14. Describa la transformación que cambiaría\(h(x)\) de las siguientes
maneras:
- Compresión vertical por un factor de 2.
- Desplazamiento horizontal a la derecha 3 unidades.
- Reflexión a través del\(y\) eje.
15. Describa la transformación que cambiaría\(f(x)\) de las siguientes
maneras:
- Estiramiento vertical por un factor de 5.
- Reflexión a través del\(x\) eje

