1.6:1.6 Simetría

Algunas funciones, como la función seno, la función de valor absoluto y la función de cuadratura, tienen simetría de reflexión a través de la línea\(x=0\). Otras funciones como la función de cubo y la función recíproca tienen simetría rotacional sobre el origen.

¿Por qué el primer grupo se categoriza como funciones pares mientras que el segundo grupo se categoriza como funciones impares?

Funciones pares e impares

Incluso Funciones

Las funciones simétricas a través de la línea\(x=0\) (el\(y\) eje) se llaman pares. Incluso las funciones tienen la propiedad de que cuando se sustituye un valor negativo\(x\), produce el mismo valor que cuando el valor positivo es sustituido por el\(x\). En otras palabras, la ecuación\(f(-x)=f(x)\) es cierta para funciones pares.

Para demostrar que la función\(f(x)=3 x^{4}-5 x^{2}+1\) es parejo, demuéstralo\(f(-x)=f(x)\).

\(\begin{aligned} f(-x) &=3(-x)^{4}-5(-x)^{2}+1 \\ &=3 x^{4}-5 x^{2}+1 \\ &=f(x) \end{aligned}\)

La propiedad de que tanto los números positivos como los negativos elevados a una potencia par sean siempre positivos es la razón por la que se utiliza el término par. No importa que los coeficientes sean pares o impares, solo los exponentes.

Funciones impares

Las funciones que tienen simetría rotacional sobre el origen se denominan funciones impares. Las funciones impares tienen la propiedad de que cuando se sustituye un\(x\) valor negativo en la función, produce una versión negativa de la función evaluada en un valor positivo. En otras palabras, la ecuación es\(f(-x)=-f(x)\) verdadera para funciones impares.

Esta propiedad adquiere cada vez más importancia en problemas y pruebas de Cálculo y más allá, pero por ahora es suficiente identificar funciones que son pares, extrañas o ninguna y mostrar por qué.

Para mostrar eso\(f(x)=4 x^{3}-x\) es extraño, demuéstralo\(f(-x)=-f(x)\).

\(\begin{aligned} f(-x) &=4(-x)^{3}-x \\ &=-4 x^{3}+x \\ &=-\left(4 x^{3}+x\right) \\ &=-f(x) \end{aligned}\)

Al igual que se nombran las funciones pares, las funciones impares se nombran porque los signos negativos no desaparecen y siempre se pueden factorizar a partir de funciones impares.

Las funciones pares e impares describen diferentes tipos de simetría, pero ambas derivan su nombre de las propiedades de los exponentes. Un número negativo elevado a un número par siempre será positivo. Un número negativo elevado a un número impar siempre será negativo.

Ejemplos

Ejemplo 1

¿Cuáles de las funciones básicas son pares, cuáles son impares y cuáles no?

Funciones pares: La función de cuadratura y la función de valor absoluto.

Funciones impares: La función de identidad, la función de cubo, la función recíproca, la función sinusoidal.

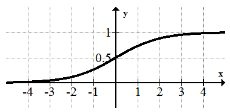
Ninguno: La función raíz cuadrada, la función exponencial y la función log. La función logística tampoco es tampoco porque es rotacionalmente simétrica sobre el punto\(\left(0, \frac{1}{2}\right)\) en lugar del origen.

Ejemplo 2

Supongamos que\(h(x)\) es una función par y\(g(x)\) es una función impar. \(f(x)=h(x)+g(x) .\)¿Es\(f(x)\) par o impar? Si\(h(x)\) es par entonces\(h(-x)=h(x)\). Si\(g(x)\) es impar entonces\(g(-x)=-g(x)\)

Por lo tanto:\(f(-x)=h(-x)+g(-x)=h(x)-g(x)\)

Esto no coincide\(f(x)=h(x)+g(x)\) ni coincide\(-f(x)=-h(x)-g(x)\)

Esta es una prueba que muestra la suma de una función par y una función impar nunca será en sí misma par o impar.

Ejemplo 3

Determina si la siguiente función es par, impar o ninguna.

\(f(x)=x\left(x^{2}-1\right)\left(x^{4}+1\right)\)

Identificar si la función es par, impar o ninguna y explicar por qué.

\(\begin{aligned} f(x) &=x\left(x^{2}-1\right)\left(x^{4}+1\right) \\ f(-x) &=(-x)\left((-x)^{2}-1\right)\left((-x)^{4}+1\right) \\ &=-x\left(x^{2}-1\right)\left(x^{4}+1\right) \\ &=-f(x) \end{aligned}\)

La función es impar porque\(f(-x)=-f(x)\) es verdadera.

\(f(x)=4 x^{3}-|x|\)]

\(\begin{aligned} f(-x) &=4(-x)^{3}-x \\ &=-4 x^{3}-x \end{aligned}\)

Esto no parece coincidir\(f(x)=4 x^{3}-|x|\) ni tampoco\(-f(x)=-4 x^{3}+|x| .\) por lo tanto, esta función no es ni par ni impar.

Nota: Esta función es una diferencia de una función impar y una función par. Esto debería ser una pista de que la función resultante no es ni par ni impar.

Revisar

Determina si las siguientes funciones son pares, impares o ninguna.

1. \(f(x)=-4 x^{2}+1\)
2. \(g(x)=5 x^{3}-3 x\)
3. \(h(x)=2 x^{2}-x\)
4. \(j(x)=(x-4)(x-3)^{3}\)
5. \(k(x)=x\left(x^{2}-1\right)^{2}\)
6. \(f(x)=2 x^{3}-5 x^{2}-2 x+1\)
7. \(g(x)=2 x^{2}-4 x+2\)
8. \(h(x)=-5 x^{4}+x^{2}+2\)

9. Supongamos que\(h(x)\) es par y\(g(x)\) es impar. Demostrar que
no\(f(x)=h(x)-g(x)\) es ni par ni impar.
10. Supongamos que\(h(x)\) es par y\(g(x)\) es impar. Demostrar que\(f(x)=\frac{h(x)}{g(x)}\) es extraño.
11. Supongamos que\(h(x)\) es par y\(g(x)\) es impar. Demostrar que\(f(x)=h(x) \cdot g(x)\) es extraño.

12. ¿La suma de dos funciones pares es siempre una función par? Explique.

13. ¿La suma de dos funciones impares es siempre una función impar? Explique.

14. ¿Por qué algunas funciones no son ni pares ni impares?

15. Si sabes que una función es par o impar, ¿qué te dice eso sobre la simetría de la función?