2.6: Resolver ecuaciones racionales

Las técnicas para resolver ecuaciones racionales son extensiones de técnicas que ya conoces. Recordemos que cuando hay fracciones en una ecuación se puede multiplicar por el denominador para borrar la fracción. La misma técnica ayuda a convertir expresiones racionales en polinomios que ya sabes resolver. Cuando se multiplica por una constante no hay problema, pero cuando se multiplica por un valor que varía y posiblemente podría ser cero cosas interesantes suceden.

Dado que cada ecuación es trivialmente cierta cuando ambos lados se multiplican por cero, ¿cómo se tiene en cuenta esto al resolver ecuaciones racionales?

Encontrar soluciones a ecuaciones racionales

El primer paso para resolver ecuaciones racionales es transformar la ecuación en una ecuación polinómica. Esto se logra limpiando la fracción, lo que significa multiplicar toda la ecuación por el denominador común de todas las expresiones racionales. Entonces deberías resolver usando lo que ya sabes. Lo último que hay que verificar una vez que se tienen las soluciones es que no hacen que los denominadores de ninguna parte de la ecuación sean iguales a cero cuando se sustituyan de nuevo en la ecuación original. Si es así, esa solución se llama externa y es una solución “falsa” que se introdujo cuando ambos lados de la ecuación se multiplicaron por un número que resultó ser cero.

Tome la siguiente ecuación racional:

\(x-\frac{5}{x+3}=12\)

Para encontrar las soluciones de la ecuación, primero multiplique todas las partes de la ecuación por\((x+3),\) el denominador común, y luego simplifique.

\(\begin{aligned} x(x+3)-5 &=12(x+3) \\ x^{2}+3 x-5-12 x-36 &=0 \\ x^{2}-9 x-41 &=0 \\ x &=\frac{-(-9) \pm \sqrt{(-9)^{2}-4 \cdot 1 \cdot(-41)}}{2 \cdot 1} \\ x &=\frac{9 \pm 7 \sqrt{5}}{2} \end{aligned}\)

La única solución externa potencial habría sido -3 ya que ese es el número que hace que el denominador de la ecuación original sea cero. Por lo tanto, ambas respuestas son posibles.

Ejemplos

Ejemplo 1

Anteriormente, se le pidió dar cuenta de las soluciones adicionales introducidas cuando ambos lados de una ecuación se multiplican por una variable. Para poder lidiar con las posibles soluciones extra, se debe verificar cada solución para ver si hace cero el denominador de alguna fracción en la ecuación original. Si lo hace, se llama solución ajena.

Ejemplo 2

Resuelve la siguiente ecuación racional

\(\frac{3 x}{x+4}-\frac{1}{x+2}=-\frac{2}{x^{2}+6 x+8}\)

Multiplica cada parte de la ecuación por el denominador común de\(x^{2}+6 x+8=(x+2)(x+4)\)

\(\begin{aligned}(x+2)(x+4)\left[\frac{3 x}{x+4}-\frac{1}{x+2}\right] &=\left[\frac{-2}{(x+2)(x+4)}\right](x+2)(x+4) \\ 3 x(x+2)-(x+4) &=-2 \\ 3 x^{2}+6 x-x-2 &=0 \\ 3 x^{2}+5 x-2 &=0 \\(3 x-1)(x+2) &=0 \\ x &=\frac{1}{3},-2 \end{aligned}\)

Tenga en cuenta que -2 es una solución ajena. La única solución real es\(x=\frac{1}{3}\).

Ejemplo 3

Resolver la siguiente ecuación racional para\(y\).

\(x=2+\frac{1}{2+\frac{1}{y+1}}\)

Esta pregunta se puede hacer de múltiples maneras. Se puede utilizar la técnica de aclaramiento de fracciones dos veces.

\(\begin{aligned}\left(2+\frac{1}{y+1}\right) x &=\left[2+\frac{1}{2+\frac{1}{y+1}}\right]\left(2+\frac{1}{y+1}\right) \\ 2 x+\frac{x}{y+1} &=2\left(2+\frac{1}{y+1}\right)+1 \\ 2 x+\frac{x}{y+1} &=4+\frac{2}{y+1}+1 \\(y+1)\left[2 x+\frac{x}{y+1}\right] &=\left[5+\frac{2}{y+1}\right](y+1) \\ 2 x(y+1)+x &=5(y+1)+2 \\ 2 x y+2 x+x &=5 y+5+2 \end{aligned}\)

Ahora solo lleva la\(y\) variable a un lado de la ecuación y todo lo demás al otro lado.

\(\begin{aligned} 2 x y-5 y &=-3 x+7 \\ y(2 x-5) &=-3 x+7 \\ y &=\frac{-3 x+7}{2 x-5} \end{aligned}\)

Ejemplo 4

Resuelve la siguiente ecuación racional.

\(\frac{3 x}{x-5}+4=x\)

\(\frac{3 x}{x-5}+4=x\)

\(\begin{aligned} 3 x+4 x-20 &=x^{2}-5 x \\ 0 &=x^{2}-12 x+20 \\ 0 &=(x-2)(x-10) \\ x &=2,10 \end{aligned}\)

Ninguna solución es ajena.

Ejemplo 5

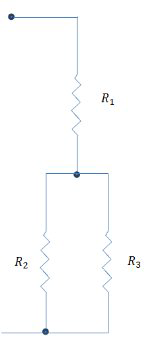
En los circuitos eléctricos, la resistencia se puede resolver por el uso de expresiones racionales. Se trata de un diagrama de circuito eléctrico con tres resistencias. La primera resistencia\(R_{1}\) se ejecuta en serie a las otras dos resistencias\(R_{2}\) y\(R_{3}\) que se ejecutan en paralelo. Si la resistencia total\(R\) es de 100 ohmios y\(R_{1}\) y cada uno\(R_{3}\) son 22 ohmios, ¿de qué es la resistencia\(R_{2}\)?

La ecuación de valor es:

\(R=R_{1}+\frac{R_{2} R_{3}}{R_{2}+R_{3}}\)

\(R=R_{1}+\frac{R_{2} R_{3}}{R_{2}+R_{3}}\)

\(\begin{aligned} 100 &=22+\frac{x \cdot 22}{x+22} \\ 78(x+22) &=22 x \\ 78 x+1716 &=22 x \\ 56 x &=-1716 \\ x &=-30.65 \end{aligned}\)

Una pregunta de seguimiento sería preguntar si los ohmios pueden ser negativos o no, lo que está más allá del alcance de este texto.

Revisar

Resolver las siguientes ecuaciones racionales. Identificar cualquier solución ajena.

1. \(\frac{2 x-4}{x}=\frac{16}{x}\)

2. \(\frac{4}{x+1}-\frac{x}{x+1}=2\)

3. \(\frac{5}{x+3}+\frac{2}{x-3}=1\)

4. \(\frac{3}{x-4}-\frac{5}{x+4}=6\)

5. \(\frac{x}{x+1}-\frac{6}{x+2}=4\)

6. \(\frac{x}{x-4}-\frac{4}{x-4}=8\)

7. \(\frac{4 x}{x-2}+3=1\)

8. \(\frac{-2 x}{x+1}+6=-x\)

9. \(\frac{1}{x+2}+1=-2 x\)

10. \(\frac{-6 x-3}{x+1}-3=-4 x\)

11. \(\frac{x+3}{x}-\frac{3}{x+3}=\frac{6}{x^{2}+3 x}\)

12. \(\frac{x-4}{x}-\frac{2}{x-4}=\frac{8}{x^{2}-4 x}\)

13. \(\frac{x+6}{x}-\frac{2}{x+6}=\frac{12}{x^{2}+6 x}\)

14. \(\frac{x+5}{x}-\frac{3}{x+5}=\frac{15}{x^{2}+5 x}\)

15. Explique lo que significa que una solución sea ajena.