2.1.7: SEC CSC COT
- Page ID
- 107624
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Valores secantes, cosecantes, cotangentes de ángulos comunes
Mientras trabajas para pintar la escalera de tu abuelo, estás mirando la forma triangular que hace la pared que sostiene las escaleras. La escalera se ve así:

Estás pensando en todas las posibles relaciones entre lados. Ya sabes que hay tres relaciones comunes, llamadas seno, coseno y tangente.
¿Cuántos otros puedes encontrar?
Secante, cosecante y cotangente Funciones
Podemos definir tres funciones más también basadas en un triángulo rectángulo. Son los recíprocos de seno, coseno y tangente.
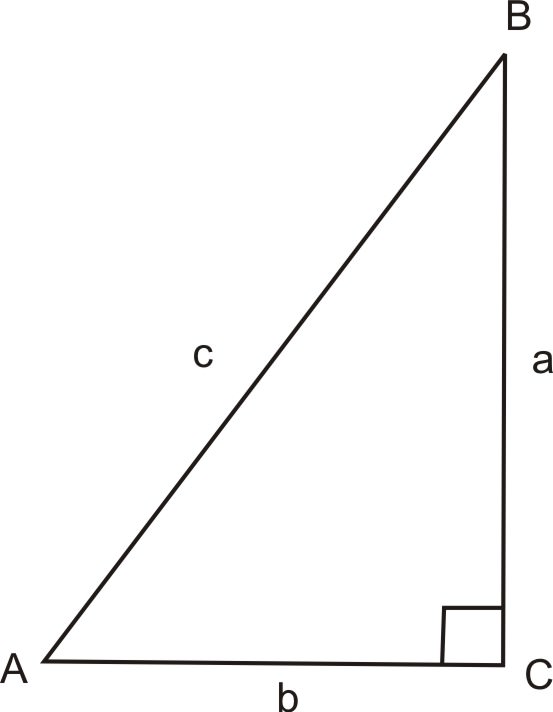
Si\(\sin A=\dfrac{a}{c}\), entonces la definición de cosecante, o csc, es\(\csc A=\dfrac{c}{a}\).
Si\(\cos A=\dfrac{b}{c}\), entonces la definición de secante, o sec, es\(\sec A=\dfrac{c}{b}\).
Si\(\tan A=\dfrac{a}{b}\), entonces la definición de cotangente, o cuna, es\(\cot A=\dfrac{b}{a}\).
Utilizar la definición de secante, cosecante y cotangente para resolver los siguientes problemas.
1. Encuentra la secante, cosecante y cotangente del ángulo\(B\).
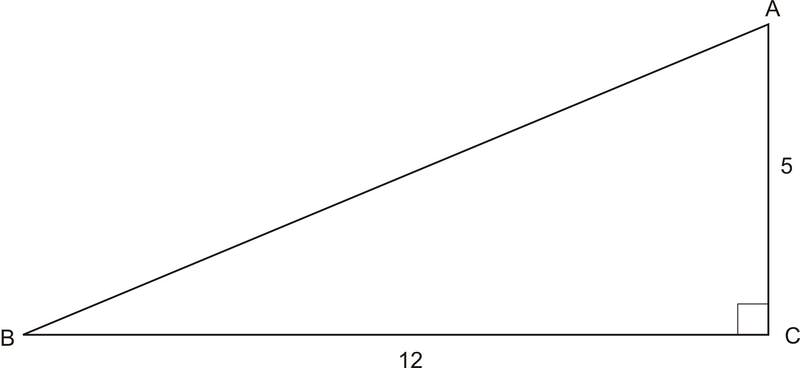
Primero, debemos encontrar la longitud de la hipotenusa. Podemos hacer esto usando el Teorema de Pitágoras:
\ (\ begin {alineado}
5^ {2} +12^ {2} &=H^ {2}\\
25+144 &=H^ {2}\\
169 &=H^ {2}\\
H &=13
\ end {alineado}\)
Ahora podemos encontrar la secante, cosecante y cotangente del ángulo B:
\ (\ begin {array} {l}
\ sec B=\ dfrac {\ text {hipotenusa}} {\ text {lado adyacente}} =\ dfrac {13} {12}\
\ csc B=\ dfrac {\ text {hipotenusa}} {\ text {lado opuesto}} =\ dfrac {13} {5}\
\ cot B=\ dfrac {\ texto {lado adyacente}} {\ texto {lado opuesto}} =\ dfrac {12} {5}
\ end {array}\)
2. Encuentra la secante, cosecante y cotangente del ángulo A
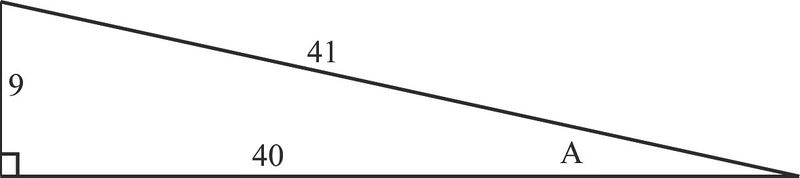
\ (\ begin {array} {l}
\ seg A=\ dfrac {\ text {hipotenusa}} {\ text {lado adyacente}} =\ dfrac {41} {40}\
\ csc A=\ dfrac {\ text {hipotenusa}} {\ text {lado opuesto}} =\ dfrac {41} {9}\
\ cot A=\ dfrac {\ texto {lado adyacente}} {\ texto {lado opuesto}} =\ dfrac {40} {9}
\ end {array}\)
3. Encuentra el seno, el coseno y la tangente del ángulo\(A\), y luego usa esto para construir la secante, cosecante y cotangente del ángulo
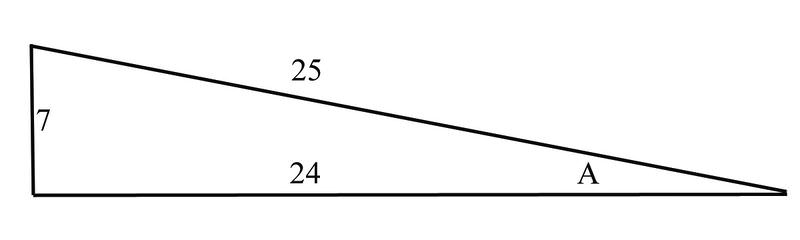
\ (\ begin {array} {l}
\ sin A=\ dfrac {\ text {lado opuesto}} {\ texto {hipotenusa}} =\ dfrac {7} {25}\
\ cos A=\ dfrac {\ texto {lado adyacente}} {\ texto {hipotenusa}} =\ dfrac {24} {25}\\
\ A=\ dfrac {\ tan texto {lado opuesto}} {\ texto {lado adyacente}} =\ dfrac {7} {24}
\ end {array}\)
Como sabemos que cosecante es el recíproco de seno, secante es el recíproco de seno, y cotangente es el recíproco de tangente, podemos construir estas funciones de la siguiente manera:
\ (\ begin {array} {l}
\ seg A=\ dfrac {1} {\ cos A} =\ dfrac {25} {24}\
\ csc A=\ dfrac {1} {\ sin A} =\ dfrac {25} {7}\
\ cuna A=\ dfrac {1} {\ tan A} =\ dfrac {24} 7}
\ end {array}\)
Antes, te dieron un problema sobre la escalera de tu abuelo.
Mirando un triángulo como la forma de la pared que sostiene la escalera de tu abuelo:

Solución
Podemos ver que hay varias formas de establecer relaciones entre las partes. En este caso, sólo nos interesan las relaciones entre los lados, lo que significa que un lado estará dividido por otro. Ya hemos visto algunas funciones, como:
1) El lado opuesto al ángulo dividido por la hipotenusa (la función sinusoidal)
2) El lado adyacente al ángulo dividido por la hipotenusa (la función coseno)
3) El lado opuesto al ángulo dividido por el lado adyacente (la función tangente)
En esta sección presentamos el recíproco de las funciones trig anteriores. Estos se encuentran tomando relaciones entre los mismos lados mostrados arriba, excepto invirtiendo el numerador y denominador:
4) La hipotenusa dividida por el lado opuesto al ángulo (la función cosecante)
5) La hipotenusa dividida por el lado adyacente al ángulo (la función secante)
6) El lado adyacente dividido por el lado opuesto (la función cotangente)
Usa la siguiente figura para ayudar a resolver los siguientes ejemplos.
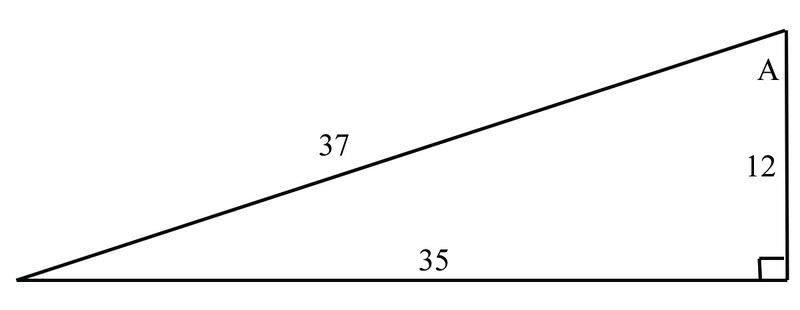
Encuentra a la secante\(\angle A\)
Solución
La función secante se define como\(\dfrac{1}{\cos}\). Ya que\(\cos=\dfrac{\text{adjacent}}{\text{hypotenuse}}\),\(\sec=\dfrac{\text{hypotenuse}}{\text{adjacent}}\).
\(\sec=\dfrac{\text{hypotenuse}}{\text{adjacent}}=\dfrac{37}{12}\approx 3.08\)
Encuentra el cosecante de\(\angle A\)
Solución
La función cosecante se define para ser\(\dfrac{1}{\sin}\). Ya que\(\sin=\dfrac{\text{opposite}}{\text{hypotenuse}}\),\(\csc=\dfrac{\text{hypotenuse}}{\text{opposite}}\).
\(\csc=\dfrac{\text{hypotenuse}}{\text{opposite}}=\dfrac{37}{35}\approx 1.06\)
Encuentra la cotangente de\(\angle A\)
Solución
La función cotangente se define como\(\dfrac{1}{\tan}\). Ya que\(\tan=\dfrac{\text{opposite}}{\text{adjacent}}\),\(\cot=\dfrac{\text{adjacent}}{\text{opposite}}\).
\(\cot=\dfrac{\text{adjacent}}{\text{opposite}}=\dfrac{12}{35} \approx .34\)
Revisar
Utilice el diagrama a continuación para las preguntas 1-3.
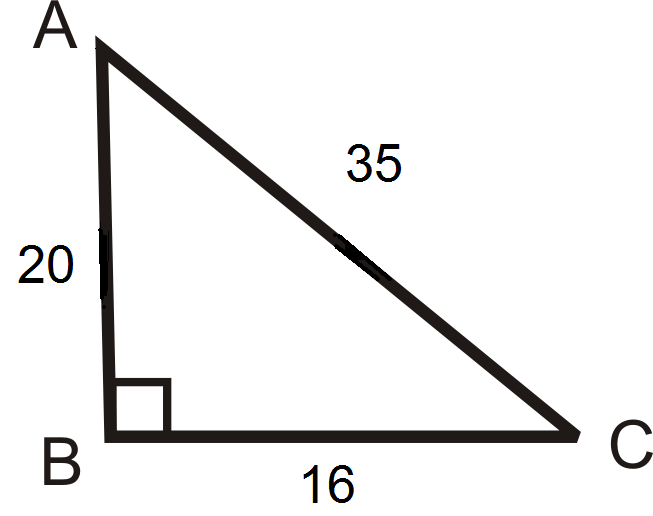
- Encontrar\(\csc A\) y\(\csc C \).
- Encontrar\(\sec A\) y\(\sec C\).
- Encontrar\(\cot A\) y\(\cot C\).
Usa el diagrama para rellenar los espacios en blanco a continuación.
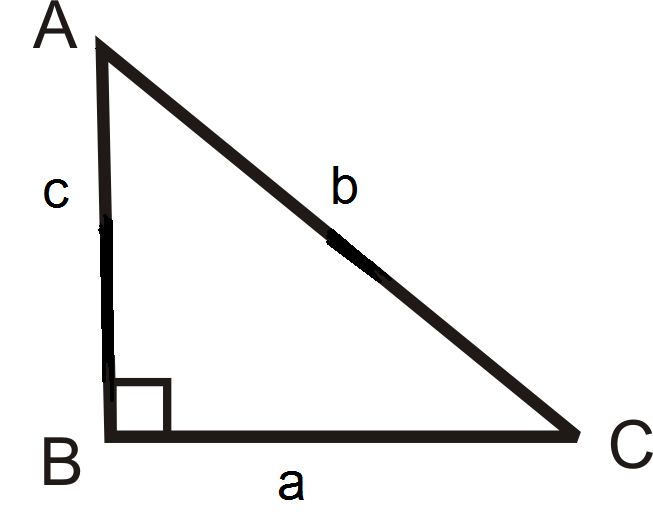
- \(\cot A=\dfrac{?}{?}\)
- \(\csc C =\dfrac{?}{?}\)
- \(\cot C=\dfrac{?}{?}\)
- \(\sec C=\dfrac{?}{?}\)
- \(\csc A=\dfrac{?}{?}\)
- \(\sec A=\dfrac{?}{?}\)
De las preguntas 4-9, podemos concluir lo siguiente. Rellene los espacios en blanco.
- \(\sec \text{_____}=\csc A\)y\(\csc \text{_____}=\sec A\).
- \(\cot A\)y\(\cot C\) son _________ el uno del otro.
- Explique por qué el csc de un ángulo siempre será mayor que 1.
- Usa tus conocimientos de triángulos 45-45-90 para encontrar la cosecante, la secante y la cotangente de un ángulo de 45 grados.
- Usa tus conocimientos de triángulos 30-60-90 para encontrar la cosecante, la secante y la cotangente de un ángulo de 30 grados.
- Usa tus conocimientos de triángulos 30-60-90 para encontrar la cosecante, la secante y la cotangente de un ángulo de 60 grados.
- A medida que aumenta el grado de un ángulo, ¿aumentará o disminuirá la cotangente del ángulo? Explique.
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 1.9.
El vocabulario
| Término | Definición |
|---|---|
| cosecante | El cosecante de un ángulo en un triángulo rectángulo es una relación que se encuentra dividiendo la longitud de la hipotenusa por la longitud del lado opuesto al ángulo dado. Este es el recíproco de la función sinusoidal. |
| cotangente | La cotangente de un ángulo en un triángulo rectángulo es una relación que se encuentra dividiendo la longitud del lado adyacente al ángulo dado por la longitud del lado opuesto al ángulo dado. Este es el recíproco de la función tangente. |
| secante | La secante de un ángulo en un triángulo rectángulo es el valor que se encuentra dividiendo la longitud de la hipotenusa por la longitud del lado adyacente al ángulo dado. La relación secante es la recíproca de la relación coseno. |

