2.6.6: Amplitud

Medida de la altura de una ola desde el eje central.

La amplitud de las funciones seno y coseno es la distancia vertical entre el eje sinusoidal y el valor máximo o mínimo de la función. En relación con las ondas sonoras, la amplitud es una medida de lo fuerte que es algo.

¿Cuál es el error más común que se comete al graficar la amplitud de una onda sinusoidal?

Amplitud de las funciones sinusoidales

La forma general de una función sinusoidal es:

\(f(x)=\pm a\cdot \sin (b(x+c))+d\)

La función coseno puede sustituirse con la misma facilidad y para muchos problemas será más fácil usar una ecuación coseno. ya que tanto las ondas sinusoidales como cosenoidales son idénticas excepto por un desplazamiento horizontal, todo depende de donde veas el inicio de la onda.

El coeficiente a es la amplitud. Cuando no hay número presente, entonces la amplitud es 1. La mejor manera de definir la amplitud es a través de una imagen. A continuación se muestra la gráfica de la función\(f(x)=3\cdot \sin x\), la cual tiene una amplitud de 3.

Figura\(\PageIndex{1}\)

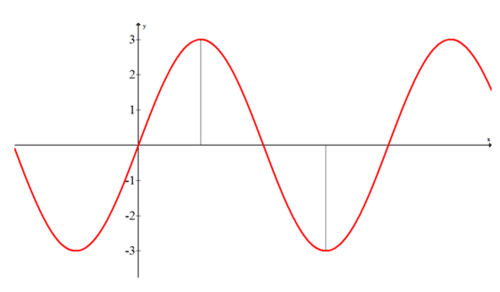
Observe que la amplitud es 3, no 6. Esto corresponde al valor absoluto de los valores máximo y mínimo de la función. Si la función hubiera sido\(f(x)=−3\cdot \sin x\), entonces toda la gráfica se reflejaría a través del eje x.

También observe que el eje x en la gráfica anterior no está etiquetado. Esto es para mostrar que la amplitud es una distancia vertical. El eje sinusoidal es la línea horizontal neutra que se encuentra entre las crestas y los valles (o picos y valles si lo prefieres). Para esta función, el eje sinusoidal era solo el eje x, pero si toda la gráfica se desplazara hacia arriba, el eje sinusoidal ya no sería el eje x. En cambio, seguiría siendo la línea horizontal directamente entre las crestas y valles que es también el promedio de los valores máximo y mínimo.

Vea la parte de este video que discute la amplitud:

Ejemplo\(\PageIndex{1}\)

Anteriormente, se le preguntó sobre el error más común que se cometía al graficar la amplitud de una onda singe. El error más común es duplicar o reducir a la mitad la amplitud innecesariamente.

Solución

Anteriormente, se le preguntó sobre el error más común que se cometía al graficar la amplitud de una onda singe. El error más común es duplicar o reducir a la mitad la amplitud innecesariamente.

Ejemplo\(\PageIndex{2}\)

Grafique la siguiente función trazando los puntos principales:\(f(x)=−2\cdot \cos x\).

Solución

La amplitud es 2, lo que significa que los valores máximos estarán en 2 y los valores mínimos estarán en -2. Normalmente con una curva coseno básica los puntos correspondientes a 0,\(\dfrac{\pi }{2}\),\(\pi\),\(\dfrac{3\pi }{2}\),\(2\pi \) caen por encima, sobre o por debajo de la línea en la siguiente secuencia: arriba, sobre, abajo, arriba. El signo negativo en la ecuación cambia arriba con abajo y abajo con arriba. Toda la gráfica se refleja a través del eje x.

Figura\(\PageIndex{2}\)

Ejemplo\(\PageIndex{3}\)

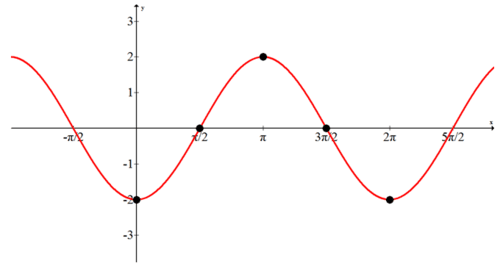
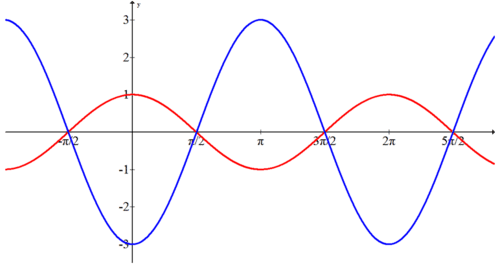
Escribe una ecuación coseno para cada una de las siguientes funciones.

Figura\(\PageIndex{3}\)

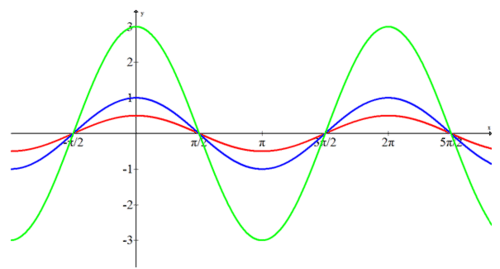
Solución

Las amplitudes de las tres funciones son 3, 1\(\dfrac{1}{2}\) y ninguna de ellas se refleja a través del eje x.

\(\begin{aligned} f(x)&=3\cdot \cos x \\ h(x)&=\cos x \\ g(x)&=\dfrac{1}{2}\cdot \cos x \end{aligned}\)

Tenga en cuenta que la amplitud en sí es siempre positiva.

Ejemplo\(\PageIndex{4}\)

Una noria con radio de 25 pies se sienta al lado de una plataforma. El viaje comienza en la plataforma y viaja hacia abajo para comenzar. Modele la altura versus el tiempo del viaje.

Solución

ya que no se da información sobre el tiempo, simplemente etiquetar el eje x como tiempo. En el tiempo cero la altura es cero. Inicialmente la altura disminuirá a medida que el paseo vaya por debajo de la plataforma. Eventualmente, la rueda encontrará el mínimo y comenzará a aumentar nuevamente hasta llegar a un máximo.

Figura\(\PageIndex{4}\)

Ejemplo\(\PageIndex{5}\)

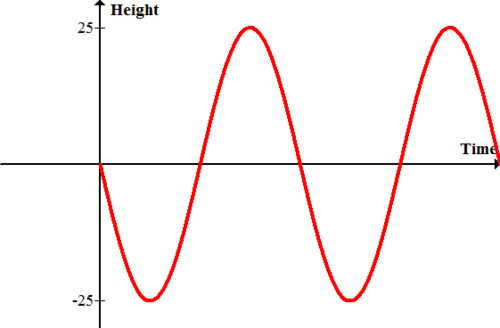
Encuentra la amplitud de la función\(f(x)=−3\cos x\) y usa el lenguaje de transformaciones para describir cómo se relaciona la gráfica con la función padre\(y=\cos x\).

Solución

La nueva función se refleja a través del eje x y se estira verticalmente por un factor de 3.

Figura\(\PageIndex{5}\)

Revisar

1. Explicar cómo encontrar la amplitud de una función sinusoidal a partir de su ecuación.
2. Explicar cómo encontrar la amplitud de una función sinusoidal a partir de su gráfica.

Encuentra la amplitud de cada una de las siguientes funciones.

3. \(g(x)=−5\cos x\)

4. 

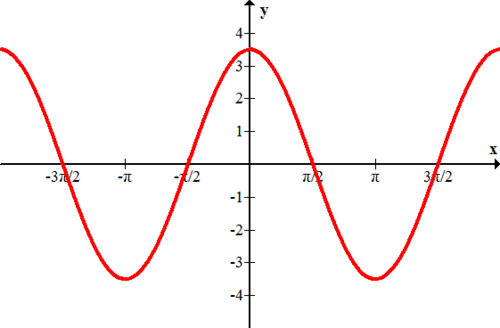
   Figura\(\PageIndex{6}\)

5. \(f(x)=\dfrac{1}{2} \sin x\)

6. 

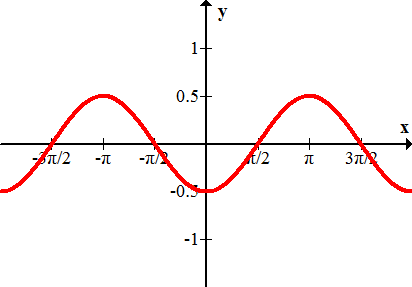
   Figura\(\PageIndex{7}\)

7. \(j(x)=3.12\cos x\)

8. 

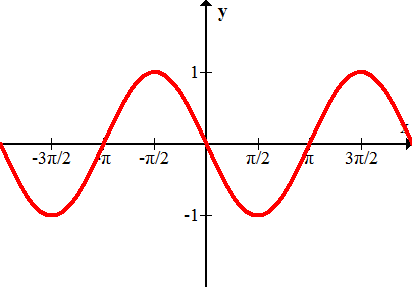
   Figura\(\PageIndex{8}\)

Esboce cada una de las siguientes funciones.

9. \(f(x)=3\sin x\)

10. \(g(x)=−4\cos x\)

11. \(h(x)=\pi \sin x\)

12. \(k(x)=−1.2\cos x\)

13. \(p(x)=\dfrac{2}{3} \cos x\)

14. \(m(x)=−\dfrac{1}{2} \sin x\)

15. Vista previa:\(r(x)=3\sin x+2\)

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 5.3.

Recursos adicionales

Video: Amplitud y Periodo de seno y coseno