2.6.8: Identidades trigonométricas y ecuaciones
- Page ID
- 107626
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Basado en amplitud, frecuencia y traducciones horizontales y verticales.
Tu profesor de matemáticas ha decidido darte un cuestionario para ver si reconoces cómo combinar los cambios en las gráficas de las funciones sinusoidales y cosenales. Recuerdas que has aprendido a cambiar las gráficas, así como a estirarlas o dilatarlas. Pero ahora tu profesor quiere ver si sabes combinar ambos efectos en una sola gráfica. Ella te da la ecuación:
\(f(x)=3+7\sin \left(4\left(x+\dfrac{\pi }{2}\right)\right)\)
y le pide que trazar la ecuación, para luego identificar lo que hace cada parte de la ecuación anterior para cambiar la gráfica.
Identidades trigonométricas y ecuaciones
Las ecuaciones generales para traducir y dilatar las ondas sinusoidales y cosenales tanto horizontal como verticalmente son:\(y=D\pm A\cos (B(x\pm C))\) o\(y=D\pm A\sin (B(x\pm C))\), donde A es la amplitud, B es la frecuencia, C es la traslación horizontal y D es la traslación vertical.
Recordemos la relación entre periodo, p, y frecuencia, B.
\(p=\dfrac{2\pi }{B}\)y\(B=\dfrac{2\pi }{p}\)
Con este conocimiento, deberíamos poder esbozar cualquier función sinusoidal o coseno así como escribir una ecuación dada su gráfica.
Echemos un vistazo a algunos problemas que involucran identidades y ecuaciones trigonométricas.
1. Dada la función:\(f(x)=1+2\sin (2(x+\pi ))\)
a. Identificar el periodo, amplitud y frecuencia.
De la ecuación, la amplitud es 2 y la frecuencia también es 2. Para encontrar el periodo utilizamos:
\(p=\dfrac{2\pi }{B}\rightarrow p=\dfrac{2\pi }{2}=\pi\)
Entonces, hay dos ondas completas de\([0,2\pi ]\) y cada onda individual requiere\(\pi \) radianes para completarse.
b. Explicar cualquier traducción vertical u horizontal presente en la ecuación.
\(D=1\)y\(C=−\pi \), por lo que esta gráfica se ha traducido 1 unidad hacia arriba, y\ pi unidades a la izquierda.
c. Esbozar la gráfica de\(-2 \pi\) a\(2 \pi\).
Para bosquejar la gráfica, comience con la gráfica de\(y=\sin (x)\)
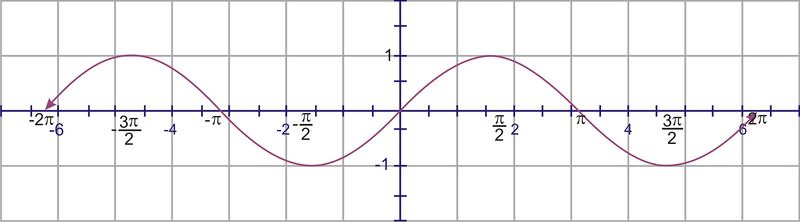
Traducir las\(\pi \) unidades gráficas a la izquierda (el valor C).
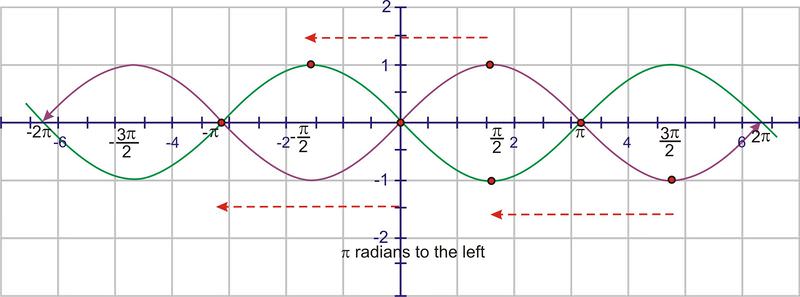
A continuación, mueva la gráfica 1 unidad hacia arriba (valor D)
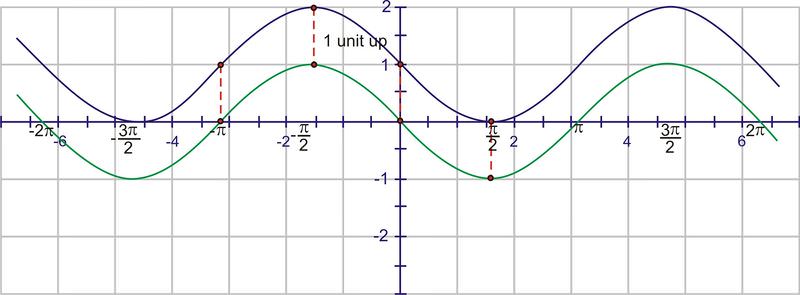
Ahora podemos agregar las dilataciones. Recuerda que el “punto de partida” de la ola es\(−\pi \) por la traslación horizontal. Una onda sinusoidal normal toma\(2 \pi\) unidades para completar un ciclo, pero esta onda completa un ciclo en\(\pi \) unidades. La primera ola se completará en 0, luego veremos una segunda ola de 0 a\(\pi \) y una tercera de\(\pi \) a\(2 \pi\). Comience colocando puntos en estos valores:

Usando la simetría, cada intervalo necesita cruzar la línea\(y=1\) a través del centro de la onda.
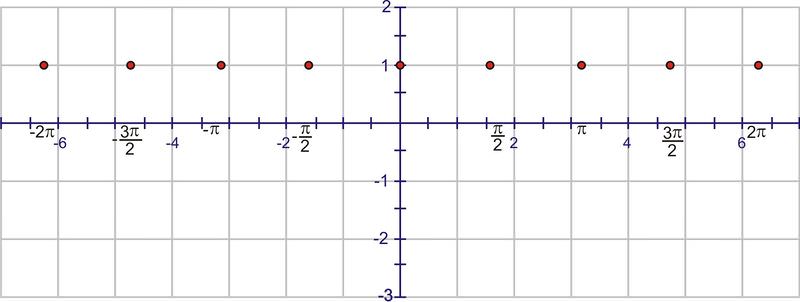
Una onda sinusoidal contiene una “montaña” y un “valle”. El “pico” de la montaña y el punto bajo del valle deben ocurrir a medio camino entre los puntos de arriba.
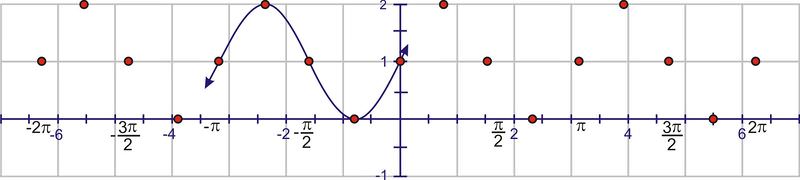
Extender la curva a través del dominio.
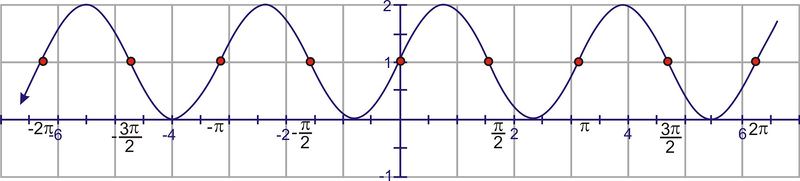
Por último, extender los puntos mínimo y máximo para que coincidan con la amplitud de 2.
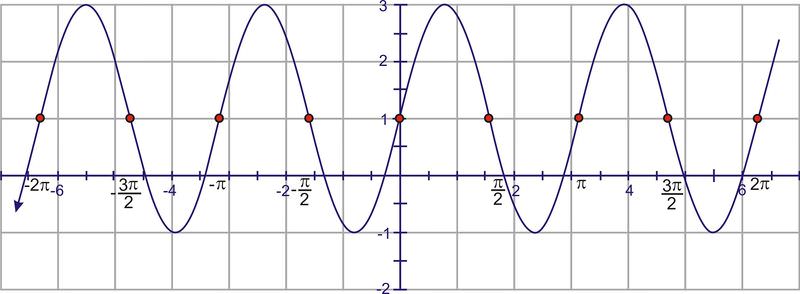
2. Dada la función:\(f(x)=3+3\cos \left(\dfrac{1}{2}\left(x−\dfrac{\pi }{2}\right)\right)\)
a. Identificar el periodo, amplitud y frecuencia.
De la ecuación, la amplitud es 3 y la frecuencia es\(\dfrac{1}{2}\). Para encontrar el periodo utilizamos:
\(\text{period}=\dfrac{2\pi }{\dfrac{1}{2}}=4\pi\)
Entonces, solo hay la mitad de una curva coseno de 0 a\(2 \pi\) y cada onda individual requiere\(4\pi \) radianes para completarse.
b. Explicar cualquier traducción vertical u horizontal presente en la ecuación.
\(D=3\)y\(C=\dfrac{\pi }{2}\), por lo que esta gráfica se ha traducido 3 unidades hacia arriba, y\(\dfrac{\pi }{2}\) unidades a la derecha.
c. Esbozar la gráfica de\(-2 \pi\) a\(2 \pi\).
Para bosquejar la gráfica, comience con la gráfica de\(y=\cos (x)\)
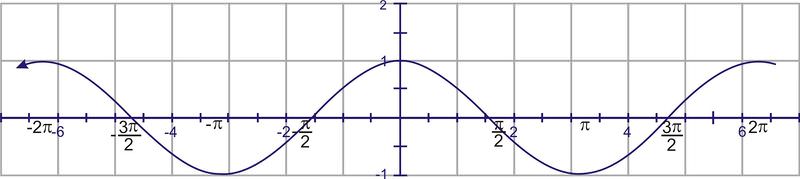
Ajusta la amplitud para que la onda coseno alcance hasta 3 y baje a tres negativos. Esto afecta a los puntos máximos, pero los puntos en el eje x siguen siendo los mismos. Estos puntos a veces se llaman nodos.
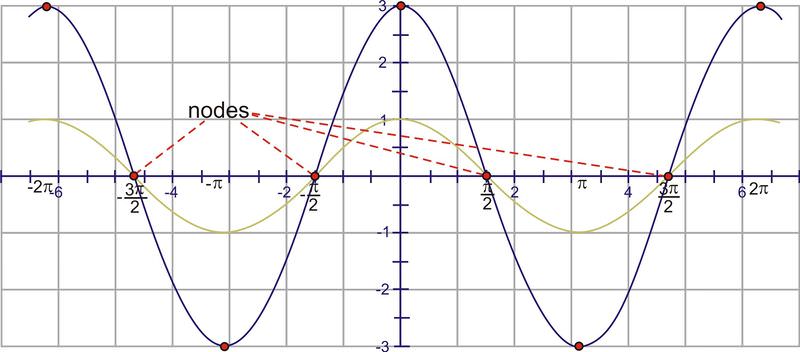
Según el periodo, deberíamos ver una de estas formas cada\(4\pi \) unidad. Porque el intervalo especificado es\([−2\pi ,2\pi ]\) y la curva coseno “comienza” en el eje y, en\((0, 3)\) y en\(2\pi \) el valor es -3. Por el contrario\(−2\pi \), at, la función también es -3.
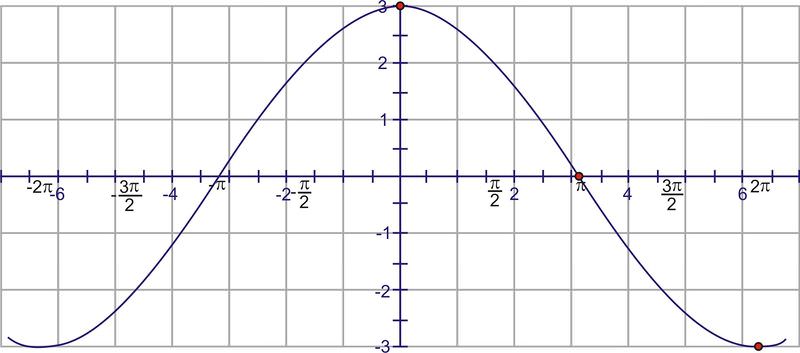
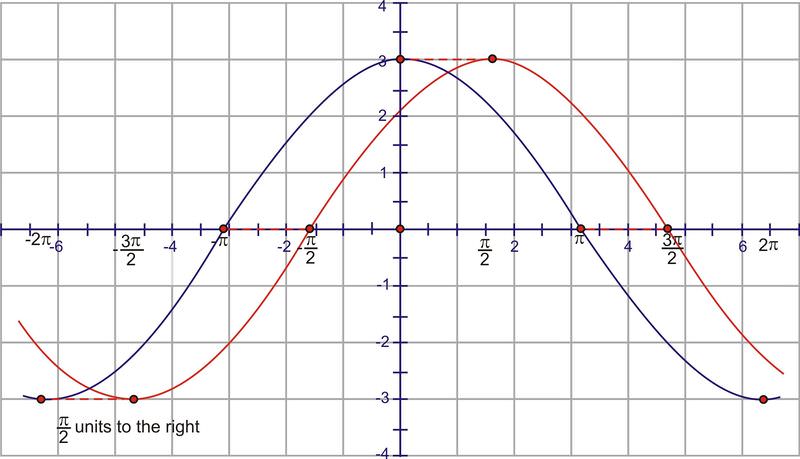
Ahora, desplaza las\(\dfrac{\pi }{2}\) unidades gráficas hacia la derecha.
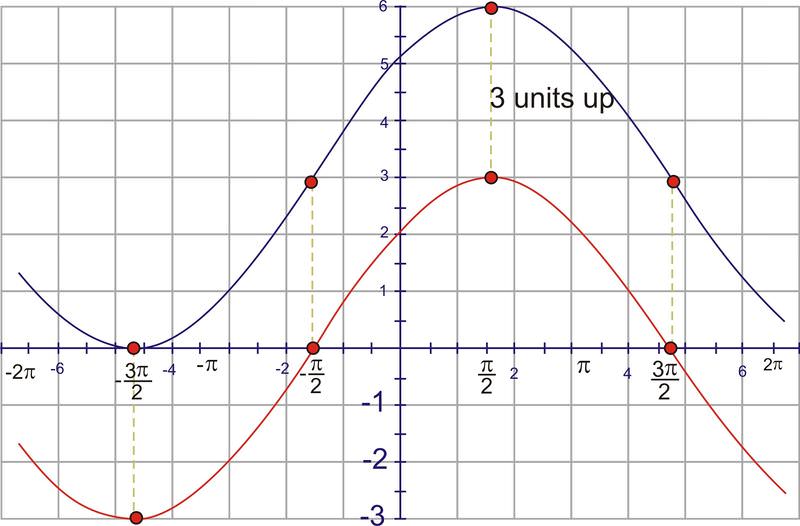
Por último, necesitamos ajustar para el desplazamiento vertical moviéndolo hacia arriba 3 unidades.
3. Encuentra la ecuación de la sinusoide graficada aquí.
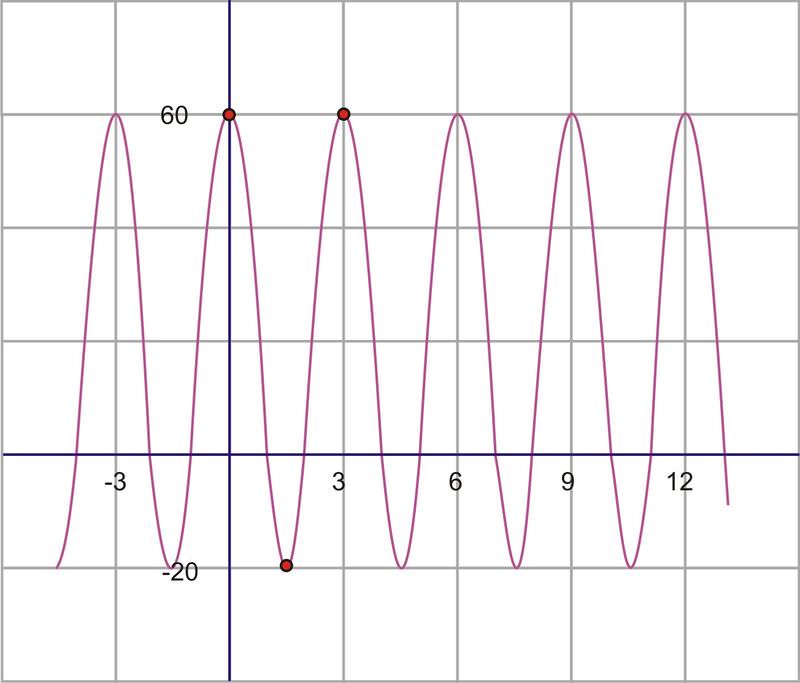
En primer lugar, recuerde que ya sea seno o coseno podría ser utilizado para modelar estas gráficas. Sin embargo, suele ser más fácil usar coseno porque el desplazamiento horizontal es más fácil de localizar en la mayoría de los casos. Por lo tanto, el modelo que vamos a utilizar es\(y=D\pm A\cos (B(x\pm C)) \).
Primero, si pensamos en la gráfica como una función coseno, tiene una traslación horizontal de cero. El punto máximo es también la intersección y−de la gráfica, por lo que no hay necesidad de desplazar la gráfica horizontalmente y por lo tanto,,\(C=0\). La amplitud es la altura desde el centro de la ola. Si no puedes encontrar el centro de la ola por la vista, puedes calcularlo. El centro debe estar a medio camino entre los puntos más altos y los más bajos, que es realmente el promedio del máximo y mínimo. Este valor en realidad será el desplazamiento vertical, o valor D.
\(D=\text{center}=\dfrac{60+−20}{2}=\dfrac{40}{2}=20\)
La amplitud es la altura desde la línea central, o desplazamiento vertical, ya sea al mínimo o al máximo. Entonces,\(A=60−20=40\).
El último valor a encontrar es la frecuencia. Para ello, primero debemos encontrar el periodo. El periodo es la distancia requerida para una ola completa. Para encontrar este valor, mire la distancia horizontal entre dos puntos máximos consecutivos.
En nuestra gráfica, de máximo a máximo es 3.
Por lo tanto, el periodo es 3, por lo que la frecuencia es\(B=\dfrac{2\pi }{3}\).
Ahora hemos calculado cada uno de los cuatro parámetros necesarios para escribir la ecuación. Reemplazarlos en la ecuación da:
\(y=20+40\cos \dfrac{2\pi }{3} x\)
Si hubiéramos optado por modelar esta curva con una función sinusoidal, la amplitud, el período y la frecuencia, así como el desplazamiento vertical serían todos iguales. La única diferencia sería el desplazamiento horizontal. La onda sinusoidal comienza en medio de una sección inclinada hacia arriba de la curva como lo muestra el círculo rojo.
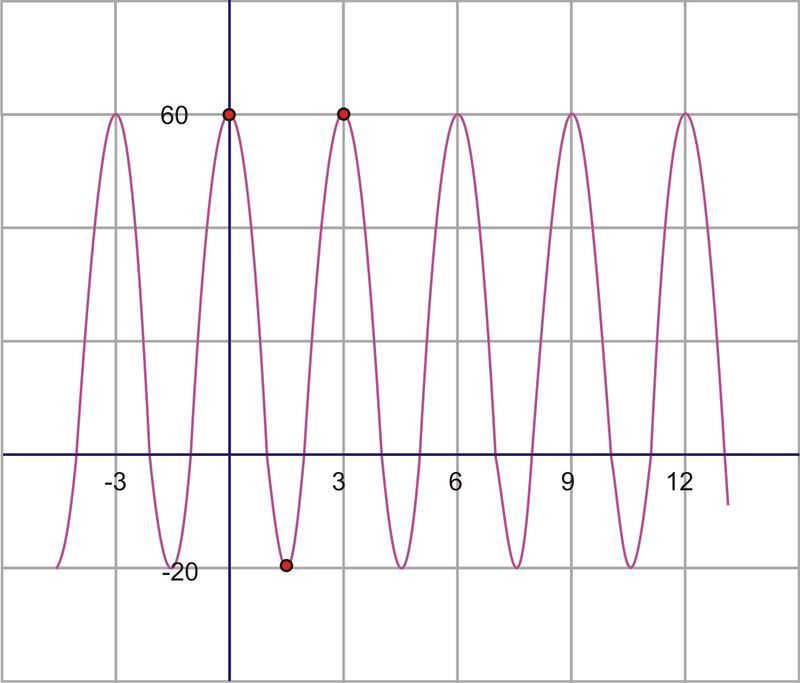
Este punto se cruza con la línea de traslación vertical y es un tercio de la distancia que se remonta a -3. Entonces, en este caso, la onda sinusoidal se ha traducido 1 unidad a la izquierda. La ecuación que usa una función sinusoidal en su lugar habría sido:\(y=20+40\sin \left(\dfrac{2\pi }{3}(x+1)\right)\)
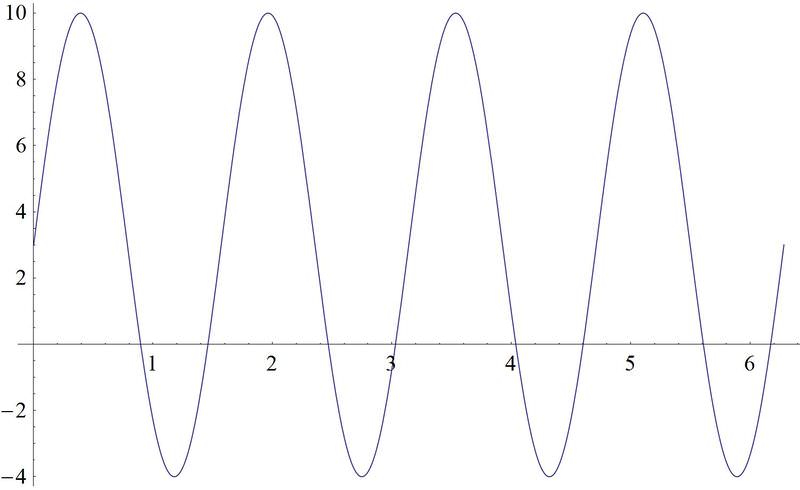
Antes, se le pidió que tramara\(f(x)=3+7\sin \left(4\left(x+\dfrac{\pi }{2}\right)\right)\).
Solución
Con su conocimiento avanzado de ecuaciones sinusoidales, puede identificar en la ecuación:
\((f(x)=3+7\sin \left(4\left(x+\dfrac{\pi }{2}\right)\right)\)
El desplazamiento vertical de la gráfica es de 3 unidades hacia arriba. La amplitud de la gráfica es 7. El desplazamiento horizontal de la gráfica es\(\dfrac{\pi }{2}\) unidades a la izquierda. La frecuencia es 4.
Dado que la frecuencia es 4, el periodo se puede calcular:
\(\begin{aligned} p&=\dfrac{2\pi}{f} \\ p&=\dfrac{2\pi }{4} \\ p&=\dfrac{\pi }{2}\end{aligned}\)
Esto significa que la gráfica toma\ pi 2 unidades para hacer un ciclo completo.
La gráfica de esta ecuación se ve así:
Identificar la amplitud, periodo, frecuencia, puntos máximo y mínimo, desplazamiento vertical y desplazamiento horizontal de\(y=2+3\sin (2(x−1))\).
Solución
Se trata de una onda sinusoidal que se ha traducido 1 unidad a la derecha y 2 unidades hacia arriba. La amplitud es 3 y la frecuencia es 2. El periodo de la gráfica es\(\pi \). La función alcanza un punto máximo de 5 y un mínimo de -1.
Identificar la amplitud, periodo, frecuencia, puntos máximo y mínimo, desplazamiento vertical y desplazamiento horizontal de\(y=−1+\sin \left(\pi \left(x+\dfrac{\pi }{3}\right)\right)\).
Solución
Se trata de una onda sinusoidal que se ha traducido 1 unidad hacia abajo y\(\dfrac{\pi }{3}\) radianes hacia la izquierda. La amplitud es 1 y el periodo es 2. La frecuencia de la gráfica es\(\pi \). La función alcanza un punto máximo de 0 y un mínimo de -2.
Identificar la amplitud, periodo, frecuencia, puntos máximo y mínimo, desplazamiento vertical y desplazamiento horizontal de\(y=\cos (40(x−120))+5\).
Solución
Se trata de una onda coseno que se ha traducido 5 unidades hacia arriba y 120 radianes a la derecha. La amplitud es 1 y la frecuencia es 40. El periodo de la gráfica es\(\dfrac{\pi }{20}\). La función alcanza un punto máximo de 6 y un mínimo de 4.
Revisar
Para cada ecuación a continuación, identifique el periodo, amplitud, frecuencia y cualquier traducción vertical/horizontal.
- \(y=2−4\cos \left(\dfrac{2}{3}(x−3)\right)\)
- \(y=3+\dfrac{1}{2}\sin \left(\dfrac{1}{2}(x−\pi )\right)\)
- \(y=1+5\cos (4(x+\dfrac{\pi }{2}))\)
- \(y=4−\cos (2(x+1))\)
- \(y=3+2\sin (x−4)\)
Grafique cada una de las siguientes ecuaciones de\(−2\pi \) a\(2\pi \).
- \(y=1−3\sin \left(\dfrac{1}{3}(x−\pi )\right)\)
- \(y=5+12\sin \left(\dfrac{1}{2}(x−2)\right)\)
- \(y=2+\cos \left(4\left(x+\dfrac{\pi }{2}\right)\right)\)
- \(y=4+2\cos \left(2\left(x+3\right)\right)\)
- \(y=2−3\sin \left(x−\dfrac{3\pi }{2}\right)\)
Encuentra la ecuación de cada sinusoide.
-
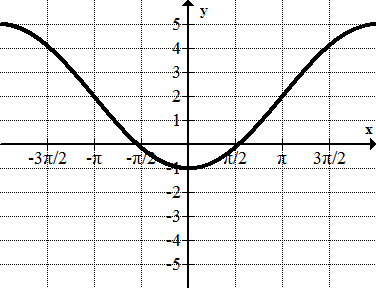
Figura\(\PageIndex{19}\) -
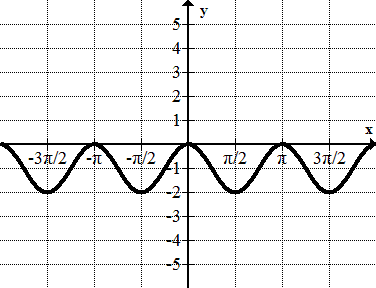
Figura\(\PageIndex{20}\) -
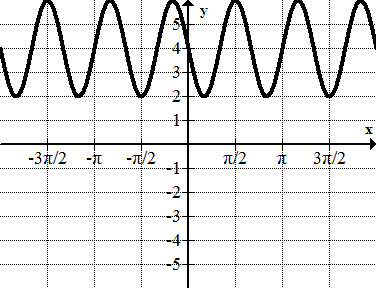
Figura\(\PageIndex{21}\) -
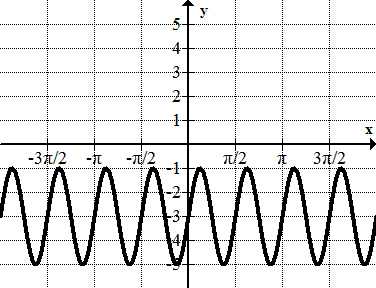
Figura\(\PageIndex{22}\) -
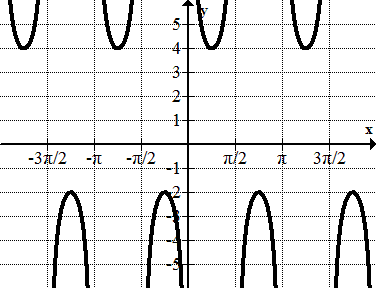
Figura\(\PageIndex{23}\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 2.17.
El vocabulario
| Término | Definición |
|---|---|
| Ecuaciones generales trigonométricas | Las ecuaciones generales trigonométricas son\(y=D\pm A\cos (B(x\pm C))\) o\(y=D\pm A\sin (B(x\pm C))\), donde A es la amplitud, B es la frecuencia, C es la traslación horizontal y D es la traslación vertical. |
Recursos adicionales
Video: Ejemplo: Graficando una Transformación de Seno y Coseno
Práctica: Identidades trigonométricas y ecuaciones

