Caso C→Q
- Última actualización
- Guardar como PDF
- Page ID
- 151234
CO-4: Distinguir entre diferentes escalas de medición, elegir los métodos estadísticos descriptivos e inferenciales adecuados con base en estas distinciones e interpretar los resultados.
REVISIÓN: Unidad 1 Caso C-Q
Video
Video: Caso C→Q (5:23)
Introducción
Recordemos la tabla de clasificación tipo rol que enmarca nuestra discusión sobre la inferencia sobre la relación entre dos variables.
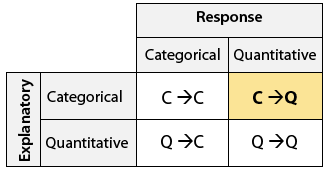
Comenzamos con el caso C→Q, donde la variable explicativa es categórica y la variable respuesta es cuantitativa.
Recordemos que en la unidad de Análisis Exploratorio de Datos, examinar la relación entre X e Y en esta situación equivale, en la práctica, a:
- Comparando las distribuciones de la respuesta (cuantitativa) Y para cada valor (categoría) de la X explicativa.
Para hacer eso, usamos
- diagramas de caja lado a lado (cada uno representa la distribución de Y en uno de los grupos definidos por X),
- y complementó la visualización con las estadísticas descriptivas correspondientes.
Tendremos que agregar una capa de dificultad aquí con la posibilidad de que podamos tener muestras emparejadas o emparejadas en lugar de muestras o grupos independientes. Obsérvese que todos los ejemplos que discutimos en el Caso CQ en la Unidad 1 consistieron en muestras independientes.
Primero revisaremos el escenario general.
Comparación de medias entre grupos
Para entender la lógica, comenzaremos con un ejemplo y luego generalizaremos.
EJEMPLO: GPA y año en la universidad
Supongamos que nuestra variable de interés es el GPA de los estudiantes universitarios en Estados Unidos. De Unint 4A, sabemos que dado que el GPA es cuantitativo, realizaremos inferencia sobre μ, el promedio de promedio (poblacional) entre todos los estudiantes universitarios estadounidenses.
Dado que esta sección trata sobre las relaciones, supongamos que lo que realmente nos interesa no es simplemente GPA, sino la relación entre:
- X: año en la universidad (1 = estudiantes de primer año, 2 = segundo año, 3 = junior, 4 = senior) y
- Y: GPA
En otras palabras, queremos explorar si el GPA está relacionado con el año en la universidad.
La manera de pensar sobre esto es que la población de estudiantes universitarios estadounidenses ahora se divide en 4 subpoblaciones: estudiantes de primer año, estudiantes de segundo año, juniors y seniors. Dentro de cada uno de estos cuatro grupos, nos interesa el GPA.
Por lo tanto, la inferencia debe involucrar a las 4 medias de subpoblación:
- μ 1: promedio de GPA entre estudiantes de primer año en Estados Unidos.
- μ 2: promedio de GPA entre estudiantes de segundo año en Estados Unidos
- μ 3: promedio de GPA entre jóvenes en Estados Unidos
- μ 4: promedio de GPA entre adultos mayores en Estados Unidos
Tiene sentido que la inferencia sobre la relación entre año y GPA tenga que basarse en algún tipo de comparación de estas cuatro medias.
Si inferimos que estas cuatro medias no son todas iguales (es decir, que hay algunas diferencias en el GPA a lo largo de los años en la universidad) entonces eso equivale a decir que GPA está relacionado con el año en la universidad. Resumimos este ejemplo con una figura:
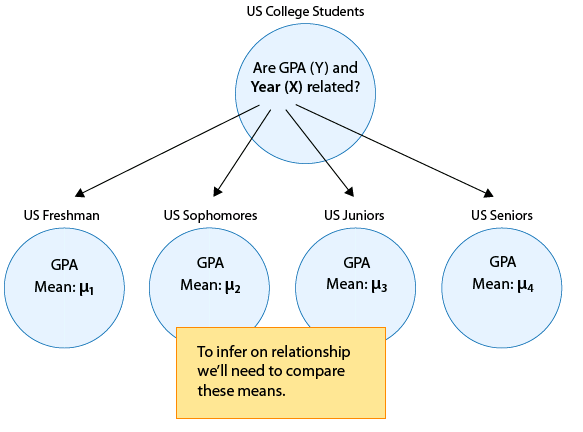
En general, hacer inferencias sobre la relación entre X e Y en el Caso C→Q se reduce a comparar las medias de Y en las subpoblaciones, las cuales son creadas por las categorías definidas por X (digamos k categorías). La siguiente figura resume esto:
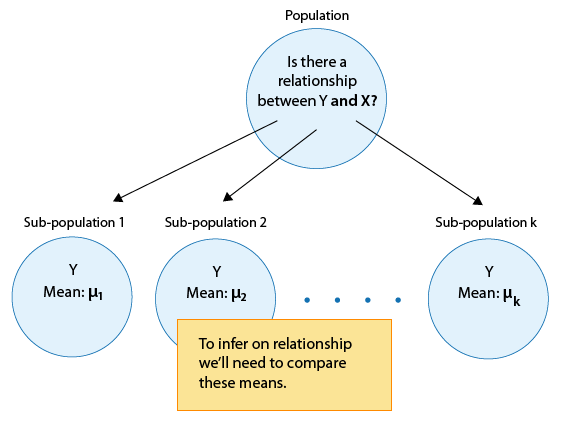
Dividiremos esto en dos escenarios diferentes (k = 2 y k > 2), donde k es el número de categorías definidas por X.
Por ejemplo:
- Si nos interesa saber si el GPA (Y) está relacionado con el género (X), este es un escenario donde k = 2 (ya que el género tiene solo dos categorías: M, F), y la inferencia se reducirá a comparar el promedio de GPA en la subpoblación de varones con el de la subpoblación de hembras.
- Por otro lado, en el ejemplo que vimos anteriormente, la relación entre GPA (Y) y año en la universidad (X) es un escenario donde k > 2 o más específicamente, k = 4 (ya que año tiene cuatro categorías).
Precaución
En términos de inferencia, ¡estas dos situaciones (k = 2 y k > 2) serán tratadas de manera diferente!
Escenario con k = 2
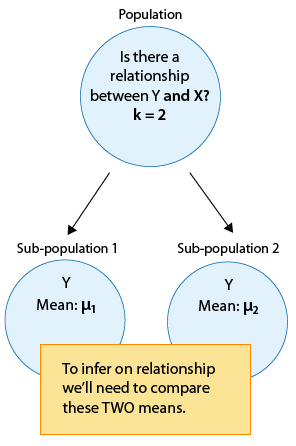
Escenario con k > 2
2. Esta gran población se divide en k subpoblaciones, cada una con su propia media μ. Para inferir sobre la relación entre Y y X, necesitaremos comparar estas k medias.” height="459" loading="lazy” src=” http://phhp-faculty-cantrell.sites.m...7/image013.gif "title="Toda la población está representada por un círculo grande, para lo cual nos preguntamos si existe una relación entre Y y X. k > 2 . Esta gran población se divide en k subpoblaciones, cada una con su propia media μ. Para inferir sobre la relación entre Y y X, necesitaremos comparar estas k medias.” width="565">
Muestras Dependientes vs Independientes (k = 2)
Objetivos de aprendizaje
LO 4.37: Identificar y distinguir entre muestras independientes y dependientes.
Además, dentro del escenario de comparar dos medias (es decir, examinar la relación entre X e Y, cuando X tiene sólo dos categorías, k = 2) distinguiremos entre dos escenarios.
Aquí, la distinción es algo sutil, y tiene que ver con cómo se eligen las muestras de cada una de las dos subpoblaciones que estamos comparando. En otras palabras, depende de qué tipo de diseño de estudio se implementará.
Hemos aprendido que muchos experimentos, así como estudios observacionales, hacen una comparación entre dos grupos (subpoblaciones) definidos por las categorías de la variable explicativa (X), a fin de ver si la respuesta (Y) difiere.
En algunas situaciones, un grupo (subpoblación 1) se define por una categoría de X, y otro grupo independiente (subpoblación 2) se define por la otra categoría de X. Luego se toman muestras independientes de cada grupo para su comparación.
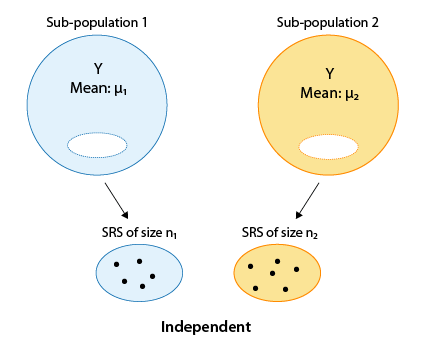
EJEMPLO:
Supongamos que estamos realizando un ensayo clínico. Los participantes son aleatorizados en dos subpoblaciones independientes:
- a quienes se les administra un medicamento y
- los que reciben un placebo.
Cada individuo aparece solo en uno de estos dos grupos y los individuos no son emparejados o emparejados de ninguna manera. Así, las dos muestras o grupos son independientes. Podemos decir que los que recibieron el medicamento son independientes de los que recibieron el placebo.
Recordar: Al asignar aleatoriamente individuos al tratamiento controlamos tanto para variables de acecho conocidas como desconocidas.
EJEMPLO:
Supongamos que la Patrulla de Caminos quiere estudiar los tiempos de reacción de los conductores con un contenido de alcohol en sangre de la mitad del límite legal en su estado.
Se diseñó un estudio observacional que también serviría de publicidad sobre el tema del consumo de alcohol y la conducción. En un gran evento donde se consumiría suficiente alcohol para obtener suficientes participantes potenciales del estudio, los oficiales montaron una carrera de obstáculos y proporcionaron los vehículos. (También se implementaron otras consideraciones para mantener el auto y las condiciones de la pista consistentes para cada participante).
Se reclutaron voluntarios de los asistentes y se les realizó una prueba de alcoholemia para determinar su contenido de alcohol en la sangre. Se eligieron dos tipos de voluntarios para participar:
- Aquellos con un contenido de alcohol en sangre de cero —medido por el alcoholímetro— de los cuales 10 fueron elegidos para impulsar el rumbo.
- Aquellos con un contenido de alcohol en sangre dentro de un rango pequeño de la mitad del límite legal (en Florida esto sería alrededor de 0.04%) —de los cuales se eligieron 9.
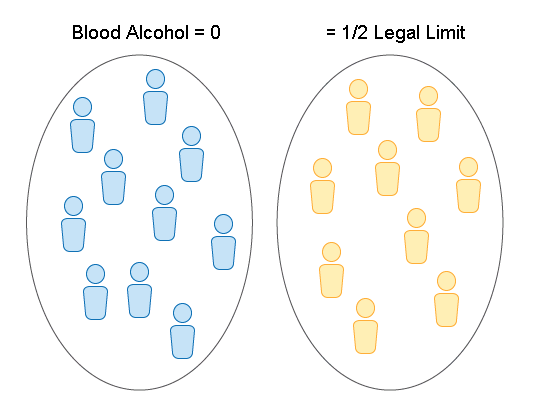
Aquí también, tenemos dos grupos independientes —aunque originalmente fueran tomados de la misma muestra de voluntarios— cada individuo aparece solo en uno de los dos grupos, la comparación de los tiempos de reacción es una comparación entre dos grupos independientes.
Sin embargo, en este estudio NO hubo asignación aleatoria al tratamiento, por lo que necesitaríamos estar mucho más preocupados por la posibilidad de que las variables acechen en este estudio en comparación con uno en el que los individuos fueron aleatorizados en uno de estos dos grupos.
Veremos que puede ser más apropiado en algunos estudios utilizar al mismo individuo como sujeto en AMBOS tratamientos, esto dará como resultado muestras dependientes.
Cuando se utiliza un diseño de muestra de pares emparejados, cada observación en una muestra se empareja, se empareja o se vincula con una observación en la otra muestra. Estas a veces se llaman “muestras dependientes”.
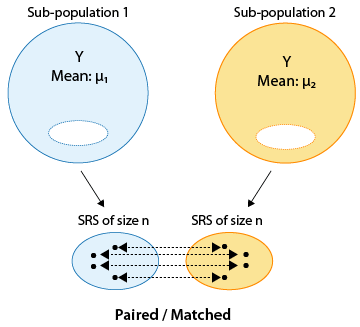
El emparejamiento podría ser por persona (si la misma persona se mide dos veces), o en realidad podría ser un par de individuos que pertenecen juntos de manera relevante (marido y mujer, hermanos).
En este diseño, entonces, se utiliza el mismo individuo o un par de individuos emparejados para realizar dos mediciones de la respuesta, una para cada uno de los dos niveles de la variable explicativa categórica.
Las ventajas de un enfoque de muestra pareada incluyen:
- Error de medición reducido ya que la varianza dentro de los sujetos suele ser menor que entre sujetos
- Requiere un número menor de sujetos para lograr el mismo poder que los métodos de muestra independientes.
Las desventajas de un enfoque de muestra pareada incluyen:
- Un efecto de orden basado en el tratamiento que los individuos recibieron primero.
- Un efecto de arrastre como un medicamento que permanece en el sistema.
- Efecto de prueba como los partícipantes aprendiendo la carrera de obstáculos en la primera carrera mejorando su desempeño en la 2da.
EJEMPLO:
Supongamos que estamos realizando un estudio sobre un bloqueador del dolor que se puede aplicar a la piel y estamos comparando dos niveles diferentes de dosificación de la solución que en este estudio se aplicará al antebrazo.
Para cada participante se aplican ambas soluciones con el siguiente protocolo:
- Qué medicamento se aplica a qué brazo es aleatorio.
- Los pacientes y el personal clínico son ciegos a las dos aplicaciones de tratamiento.
- La tolerancia al dolor se mide en ambos brazos usando la misma prueba estándar con el orden de pruebas aleatorizadas.
Aquí tenemos muestras dependientes ya que el mismo paciente aparece en ambos grupos de dosificación.
Nuevamente, la aleatorización se emplea para ayudar a minimizar otros problemas relacionados con el diseño del estudio, como un orden o efecto de prueba.
EJEMPLO:
Supongamos que el departamento de vehículos motorizados quiere comprobar si los conductores están deteriorados después de tomar dos cervezas.
Los tiempos de reacción (medidos en segundos) en una carrera de obstáculos se miden para 8 conductores seleccionados al azar antes y luego después del consumo de dos cervezas.
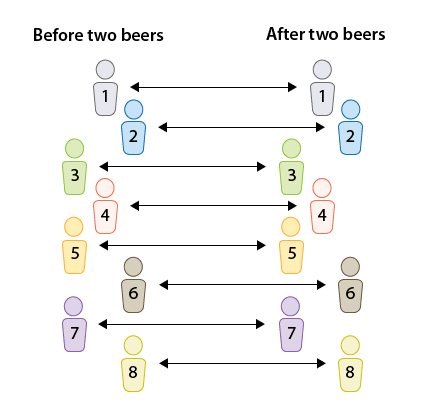
Tenemos un diseño de pares emparejados, ya que cada individuo se midió dos veces, una antes y otra después.
En pares emparejados, la comparación entre los tiempos de reacción se realiza para cada individuo.
Comentario:
- Obsérvese que en la primera figura, donde las muestras son independientes, los tamaños de muestra de las dos muestras independientes no necesitan ser los mismos.
- Por otro lado, es obvio por el diseño que en los pares emparejados los tamaños de muestra de las dos muestras deben ser los mismos (y así usamos n para ambas).
- Las muestras dependientes pueden ocurrir en muchos otros entornos pero por ahora nos enfocamos en el caso de investigar la relación entre una variable explicativa categórica de dos niveles y una variable de respuesta cuantitativa.
Resumimos:
Comenzaremos nuestra discusión de Inferencia para Relaciones con el Caso C-Q, donde la variable explicativa (X) es categórica y la variable respuesta (Y) es cuantitativa. Se discutió que la inferencia en este caso equivale a comparar medias poblacionales.
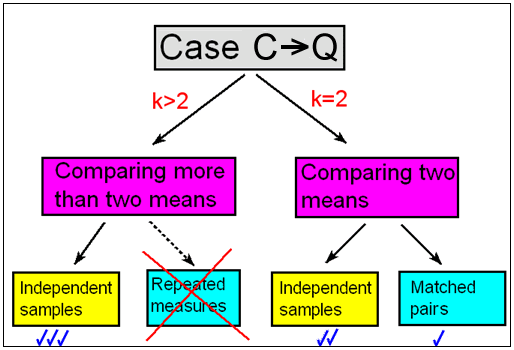
- Distinguimos entre escenarios donde la variable explicativa (X) tiene solo dos categorías y escenarios donde la variable explicativa (X) tiene MÁS de dos categorías.
- Al comparar dos medias, hacemos la mayor distinción entre situaciones en las que tenemos muestras independientes y aquellas en las que hemos emparejado pares.
- Para comparar más de dos medias en este curso, nos centraremos únicamente en la situación en la que tengamos muestras independientes. En estudios con más de dos grupos sobre muestras dependientes, es bueno saber que un método común utilizado son las medidas repetidas pero no lo cubriremos aquí.
- Primero discutiremos la comparación de dos medias poblacionales comenzando con pares emparejados (muestras dependientes) y luego muestras independientes y concluiremos comparando más de dos medias poblacionales en el caso de muestras independientes.
Ahora pon a prueba tus habilidades para identificar los tres escenarios en el Caso C-Q.
¿Conseguí esto? : Escenarios en el Caso C-Q
(Versión No Interactiva — Alerta de Spoiler)
Mirando hacia el futuro — Métodos en el Caso C-Q
- Los métodos en BOLD serán nuestro foco principal en esta unidad.
Aquí un resumen de las pruebas que aprenderemos para el escenario donde k = 2.
Muestras independientes (más énfasis) |
Muestras Dependientes (Menos Énfasis) |
Pruebas estándar
Prueba no paramétrica
|
Prueba estándar
Pruebas no paramétricas
|
Aquí un resumen de las pruebas que aprenderemos para el escenario donde k > 2.
Muestras Independientes (Solo Énfasis) |
Muestras dependientes (no discutidas) |
Pruebas estándar
Prueba no paramétrica
|
Prueba estándar
|
Muestras Pareadas
Precaución
Como mencionamos al final de la Introducción a la Unidad 4B, solo nos centraremos en las pruebas bilaterales para lo que resta de este curso. Las pruebas unilaterales son a menudo posibles, pero rara vez se utilizan en la investigación clínica.
- Introducción — Pares emparejados (prueba t pareada)
- La idea detrás de la prueba T emparejada
- Procedimiento de prueba para la prueba T pareada
- Ejemplo: Beber y conducir
- Ejemplo: Puntajes de CI
- Datos adicionales para la práctica
- Pruebas no paramétricas
- Resumimos
CO-4: Distinguir entre diferentes escalas de medición, elegir los métodos estadísticos descriptivos e inferenciales adecuados con base en estas distinciones e interpretar los resultados.
Objetivos de aprendizaje
LO 4.35: Para una situación de análisis de datos que involucre dos variables, elija el método inferencial apropiado para examinar la relación entre las variables y justificar la elección.
Objetivos de aprendizaje
LO 4.36: Para una situación de análisis de datos que involucre dos variables, llevar a cabo el método inferencial apropiado para examinar las relaciones entre las variables y sacar las conclusiones correctas en contexto.
CO-5: Determinar alternativas metodológicas preferidas a los métodos estadísticos de uso común cuando no se cumplen los supuestos.
Video
Vídeo: Muestras pareadas (27:19)
Tutoriales SAS relacionados
Tutoriales relacionados con SPSS
- 8B (2:00) EDA de diferencias
- Prueba T emparejada 8C (3:11)
- 8D (3:32) No paramétrico (emparejado)
Introducción — Pares emparejados (prueba t pareada)
Objetivos de aprendizaje
LO 4.37: Identificar y distinguir entre muestras independientes y dependientes.
Objetivos de aprendizaje
LO 4.38: En un contexto dado, determinar el método estándar apropiado para comparar grupos y proporcionar las conclusiones correctas dado el resultado del software apropiado.
Objetivos de aprendizaje
LO 4.39: En un contexto dado, establecer las hipótesis nulas y alternativas apropiadas para comparar grupos.
Estamos en el Caso CQ de inferencia sobre las relaciones, donde la variable explicativa es categórica y la variable respuesta es cuantitativa.
Como mencionamos en el resumen de la introducción al Caso C→Q, el primer caso que trataremos es el que involucra pares emparejados. En este caso:
- Las muestras están emparejadas o emparejadas. Cada observación en una muestra está vinculada con una observación en la otra muestra.
- Es decir, las muestras son dependientes.
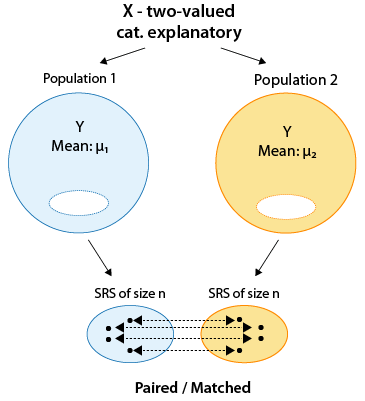
Observe a partir de este punto en adelante usaremos los términos población 1 y población 2 en lugar de subpoblación 1 y subpoblación 2. Cualquiera de las dos terminología es correcta.
Uno de los casos más comunes donde ocurren muestras dependientes es cuando ambas muestras tienen los mismos sujetos y están “emparejadas por sujeto”. Es decir, cada sujeto se mide dos veces sobre la variable de respuesta, típicamente antes y después de algún tipo de tratamiento/intervención para evaluar su efectividad.
EJEMPLO: Clase SAT Prep
Supongamos que desea evaluar la efectividad de una clase preparatoria del SAT.
Tendría sentido usar el diseño de pares emparejados y registrar el puntaje SAT de cada estudiante muestreado antes y después de que se asistan a las clases preparatorias del SAT:
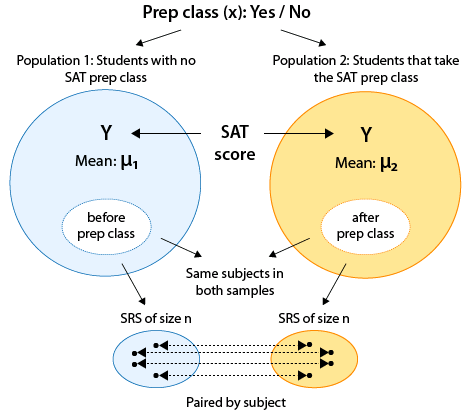
Recordemos que las dos poblaciones representan los dos valores de la variable explicativa. Ante esta situación, esos dos valores provienen de un solo conjunto de sujetos.
- Es decir, ambas poblaciones realmente tienen los mismos estudiantes.
- Sin embargo, cada población tiene un valor diferente de la variable explicativa. Esos valores son: sin clase preparatoria, clase preparatoria.
Este, sin embargo, no es el único caso en el que se utiliza el diseño emparejado. Otros casos son cuando las parejas son “parejas naturales”, como hermanos, gemelos o parejas.
Notas sobre resúmenes gráficos para datos emparejados en el Caso CQ:
- Debido a la naturaleza emparejada de este tipo de datos, realmente no podemos usar diagramas de caja lado a lado para visualizar estos datos ya que la información contenida en el emparejamiento se pierde por completo.
- Tendremos que proporcionar resúmenes gráficos de las propias diferencias para poder explorar este tipo de datos.
La idea detrás de la prueba T emparejada
La idea detrás de la prueba t pareada es reducir esta situación de dos muestras, donde estamos comparando dos medias, a una situación de una sola muestra donde estamos haciendo inferencia sobre una sola media, y luego usar una prueba t simple que introdujimos en el módulo anterior.
En esta configuración, podemos reducir fácilmente los datos sin procesar a un conjunto de diferencias y realizar una prueba t de una muestra.
- Así simplificamos nuestro procedimiento de inferencia a un problema donde estamos haciendo una inferencia sobre una sola media: la media de las diferencias.
En otras palabras, al reducir las dos muestras a una muestra de diferencias, estamos esencialmente reduciendo el problema de un problema en el que estamos comparando dos medias (es decir, haciendo inferencia en μ 1 −μ 2) a un problema en el que estamos estudiando una media.
En general, en cada problema de pares emparejados, nuestros datos constan de 2 muestras que están organizadas en n pares:
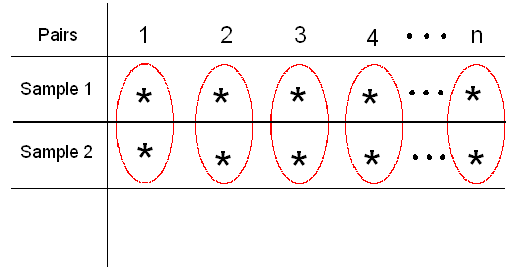
Reducimos las dos muestras a una sola calculando la diferencia entre las dos observaciones para cada par.
Por ejemplo, piense en la Muestra 1 como “antes” y la Muestra 2 como “después”. Podemos encontrar la diferencia entre los resultados antes y después para cada participante, lo que nos da una sola muestra, a saber, “antes — después”. Etiquetamos esta diferencia como “d” en la siguiente ilustración.
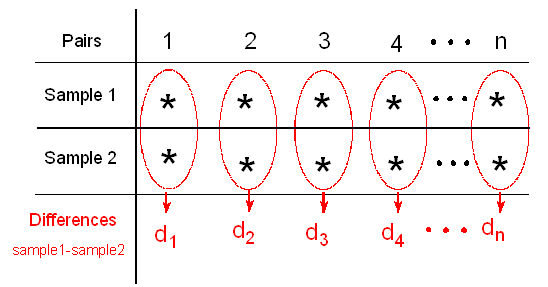
La prueba t pareada se basa en esta muestra de n diferencias,
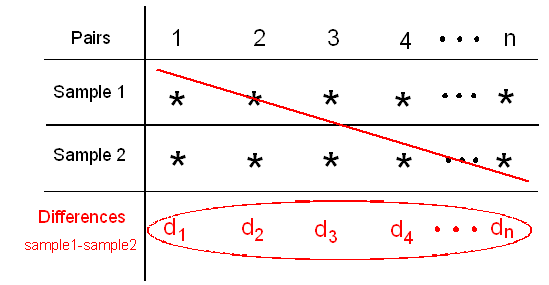
y utiliza esas diferencias como datos para una prueba t de una muestra sobre una sola media, la media de las diferencias.
Esta es la idea general detrás de la prueba t pareada; ¡no es más que una prueba t regular de una muestra para la media de las diferencias!
Procedimiento de prueba para la prueba T pareada
Ahora pasaremos por el proceso de 4 pasos de la prueba t pareada.
- Paso 1: Indicar las hipótesis
Recordemos que en la prueba t para una sola media nuestra hipótesis nula fue: Ho: μ = μ 0 y la alternativa fue una de Ha: μ < μ 0 o μ > μ 0 o μ ≠ μ 0. Dado que la prueba t pareada es un caso especial de la prueba t de una muestra, las hipótesis son las mismas excepto que:
En lugar de simplemente μ usamos la notación μ d para denotar que el parámetro de interés es la media de las diferencias.
En este curso nuestro valor nulo μ 0 es siempre 0. En otras palabras, volviendo a nuestras muestras pareadas originales, nuestra hipótesis nula afirma que no hay diferencia entre las dos medias. (Técnicamente, no tiene que ser cero si te interesa una diferencia más específica —por ejemplo, podría interesarte demostrar que hay una reducción en la presión arterial de más de 10 puntos pero no vamos a ver específicamente este tipo de situaciones).
Por lo tanto, en la prueba t pareada: La hipótesis nula es siempre:
Ho: μ d = 0
(NO HAY asociación entre la variable explicativa categórica y la variable de respuesta cuantitativa)
Nos centraremos en la hipótesis alternativa bilateral de la forma:
Ha: μ d ≠ 0
(HAY UNA asociación entre la variable explicativa categórica y la variable de respuesta cuantitativa)
A algunos estudiantes les resulta útil saber que resulta que μ d = μ 1 — μ 2 (en otras palabras, la diferencia entre las medias es la misma que la media de las diferencias). Puede que le resulte más fácil pensar primero en las hipótesis en términos de μ 1 — μ 2 y luego representarlo en términos de μ d.
¿Conseguí esto? Configuración de hipótesis
(versión no interactiva — alerta de spoiler)
- Paso 2: Obtener datos, verificar condiciones y resumir datos
La prueba t pareada, como caso especial de una prueba t de una muestra, se puede usar de manera segura siempre que:
La muestra de diferencias es aleatoria (o al menos puede considerarse aleatoria en contexto).
La distribución de las diferencias en la población debe variar normalmente si se tienen muestras pequeñas. Si el tamaño de la muestra es grande, es seguro usar la prueba t pareada independientemente de si las diferencias varían normalmente o no. Esta condición se cumple en las tres situaciones marcadas por una marca de verificación verde en la siguiente tabla.
Nota: la normalidad se verifica observando el histograma de diferencias, y siempre y cuando no sea aparente una clara violación de la normalidad (como asimetría extrema y/o valores atípicos), el supuesto de normalidad es razonable.
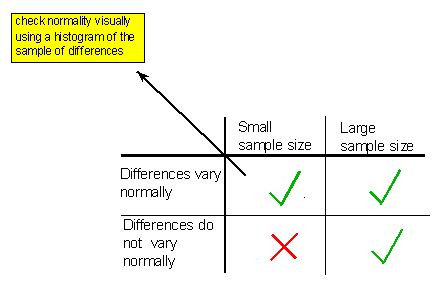
Suponiendo que podemos usar con seguridad la prueba t pareada, los datos se resumen mediante un estadístico de prueba:
\(t = \dfrac{\bar{y}_d - 0}{s_d / \sqrt{n}}\)
donde
\(\bar{y}_d = \text{ sample mean of the differences}\)
\(s_d = \text{sample standard deviation of the differences}\)
Este estadístico de prueba mide (en errores estándar) qué tan lejos están nuestros datos (representados por la media muestral de las diferencias) de la hipótesis nula (representada por el valor nulo, 0).
Observe que esta estadística de prueba tiene la misma forma general que las discutidas anteriormente:
\(\text{test statistic} = \dfrac{\text{estimator - null value}}{\text{standard error of estimator}}\)
- Paso 3: Encuentre el valor p de la prueba usando el estadístico de prueba de la siguiente manera
Como caso especial de la prueba t de una muestra, la distribución nula del estadístico de prueba t pareada es una distribución t (con n — 1 grados de libertad), que es la distribución bajo la cual se calculan los valores p. Usaremos software para encontrar el valor p para nosotros.
- Paso 4: Conclusión
Como es habitual, sacamos nuestra conclusión con base en el valor p. Asegúrese de escribir sus conclusiones en contexto especificando sus variables actuales y/o describiendo con precisión la diferencia media poblacional en términos de las variables actuales.
En particular, si se especifica una probabilidad de corte, α (nivel de significancia), rechazamos Ho si el valor p es menor que α. De lo contrario, no rechazamos a Ho.
Si el valor p es pequeño, existe una diferencia estadísticamente significativa entre lo observado en la muestra y lo que se reclamó en Ho, por lo que rechazamos Ho.
Conclusión: Existe suficiente evidencia de que la variable explicativa categórica está asociada con la variable de respuesta cuantitativa. Más específicamente, hay suficiente evidencia de que la diferencia media poblacional no es igual a cero.
Recuerda: un pequeño valor p nos dice que hay muy pocas posibilidades de obtener datos como los observados (o incluso más extremos) si la hipótesis nula fuera cierta. Por lo tanto, un pequeño valor p indica que debemos rechazar la hipótesis nula.
Si el valor p no es pequeño, no tenemos evidencia estadística suficiente para rechazar a Ho.
Conclusión: NO hay evidencia suficiente de que la variable explicativa categórica esté asociada con la variable de respuesta cuantitativa. Más específicamente, NO hay evidencia suficiente de que la diferencia media poblacional no sea igual a cero.
¡Fíjate cuánto mejor suena la primera oración! Puede resultar difícil formular correctamente estas conclusiones en términos de la diferencia de medias sin confundir los dobles negativos.
Objetivos de aprendizaje
LO 4.40: Con base en el resultado de una prueba t pareada, interpretar correctamente en contexto el intervalo de confianza apropiado para la diferencia media poblacional.
Como en métodos anteriores, podemos hacer un seguimiento con un intervalo de confianza para la diferencia de medias, μ d e interpretar este intervalo en el contexto del problema.
Interpretación: Estamos 95% seguros de que la diferencia media poblacional (descrita en contexto) es entre (límite inferior) y (límite superior).
Los intervalos de confianza también se pueden usar para determinar si rechazar o no la hipótesis nula de la prueba en función de si el valor nulo de cero cae o no fuera del intervalo o dentro.
Si el valor nulo, 0, cae fuera del intervalo de confianza, Ho es rechazado. (Cero NO es un valor plausible basado en el intervalo de confianza)
Si el valor nulo, 0, cae dentro del intervalo de confianza, Ho no es rechazado. (Cero ES un valor plausible basado en el intervalo de confianza)
NOTA: Tenga cuidado de elegir el intervalo de confianza correcto sobre la diferencia media poblacional y no los intervalos de confianza individuales para las medias en los propios grupos.
Ahora veamos un ejemplo.
EJEMPLO: Beber y conducir
Nota: En algunos de los videos presentados en los materiales del curso, realizamos la prueba unilateral para estos datos en lugar de la prueba bilateral que realizamos a continuación. En la Unidad 4B vamos a restringir nuestra atención a pruebas de doble cara complementadas con intervalos de confianza según sea necesario para brindar más información sobre el efecto de interés.
- Aquí está la Salida SPSS para este ejemplo, así como la Salida SAS y el Código SAS.
Conducir en estado de ebriedad es una de las principales causas de accidentes automovilísticos. Las entrevistas con conductores ebrios que estuvieron involucrados en accidentes y sobrevivieron revelaron que uno de los principales problemas es que los conductores no se dan cuenta de que están deteriorados, pensando “Solo comí 1-2 tragos... estoy bien para conducir”.
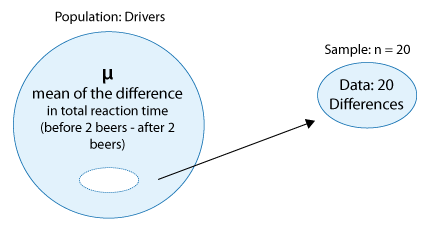
Se eligió una muestra de 20 conductores, y se midieron sus tiempos de reacción en una carrera de obstáculos antes y después de tomar dos cervezas. El propósito de este estudio fue verificar si los conductores están deteriorados después de tomar dos cervezas. Aquí hay una figura que resume este estudio:
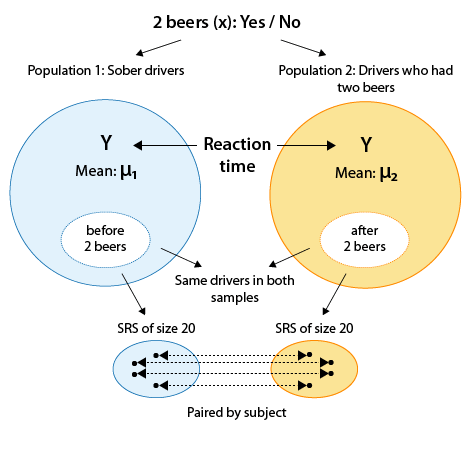
- Obsérvese que la variable explicativa categórica aquí es “beber 2 cervezas (Sí/No)”, y la variable de respuesta cuantitativa es el tiempo de reacción.
- Al utilizar el diseño de pares emparejados en este estudio (es decir, midiendo cada conductor dos veces), los investigadores aislaron el efecto de las dos cervezas en los conductores y eliminaron cualquier otro factor de confusión que pudiera influir en los tiempos de reacción (como la experiencia del conductor, la edad, etc.).
- Para cada conductor, las dos mediciones son el tiempo total de reacción antes de beber dos cervezas, y después. Puedes ver los datos siguiendo los enlaces del Paso 2 a continuación.
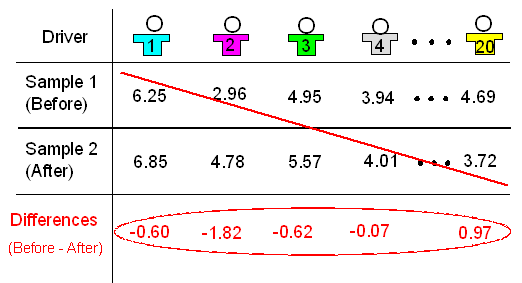
Dado que las mediciones están emparejadas, podemos reducir fácilmente los datos brutos a un conjunto de diferencias y realizar una prueba t de una muestra.
Estos son algunos de los resultados para estos datos:
Paso 1: Indicar las hipótesis
Definimos μ d = la diferencia media poblacional en los tiempos de reacción (Antes — Después).
Como mencionamos, la hipótesis nula es:
- Ho: μ d = 0 (indicando que la población de las diferencias se centra en un número que ES CERO)
La hipótesis nula afirma que las diferencias en los tiempos de reacción se centran en (o alrededor) 0, lo que indica que beber dos cervezas no tiene impacto real en los tiempos de reacción. Es decir, los conductores no se ven afectados después de tomar dos cervezas.
Aunque realmente queremos saber si sus tiempos de reacción son más largos después de las dos cervezas, todavía nos centraremos en realizar pruebas de hipótesis de dos caras. Podremos abordar si los tiempos de reacción son más largos después de dos cervezas cuando miremos el intervalo de confianza.
Por lo tanto, utilizaremos la alternativa de dos caras:
- Ha: μ d ≠ 0 (indicando que la población de las diferencias se centra en un número que NO es CERO)
Paso 2: Obtener datos, verificar condiciones y resumir datos
- Datos: Cervezas formato SPSS, formato SAS, formato Excel, formato CSV
Primero comprobemos si podemos proceder con seguridad con la prueba t pareada, comprobando las dos condiciones.
- La muestra de conductores se eligió al azar.
- El tamaño de la muestra no es grande (n = 20), por lo que para proceder, necesitamos mirar el histograma o QQ-plot de las diferencias y asegurarnos de que no hay evidencia de que no se cumpla el supuesto de normalidad.
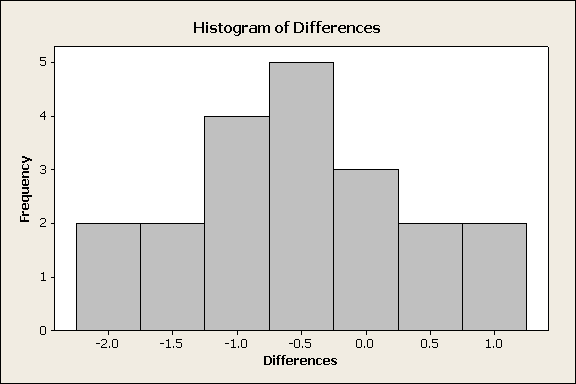
Podemos ver por el histograma anterior que no hay evidencia de violación de la suposición de normalidad (por el contrario, el histograma parece bastante normal).
También tenga en cuenta que la gran mayoría de las diferencias son negativas (es decir, los tiempos de reacción totales para la mayoría de los conductores son mayores después de las dos cervezas), lo que sugiere que los datos proporcionan evidencia contra la hipótesis nula.
La pregunta (a la que responderá el valor p) es si estos datos proporcionan evidencia suficientemente fuerte o no contra la hipótesis nula. Podemos proceder con seguridad a calcular el estadístico de prueba (que en la práctica dejamos al software para que nos calcule).
Estadística de Prueba: Utilizaremos software para calcular el estadístico de prueba que es t = -2.58.
- Recordar: Esto indica que los datos (representados por la media muestral de las diferencias) son 2.58 errores estándar por debajo de la hipótesis nula (representada por el valor nulo, 0).
Paso 3: Encuentre el valor p de la prueba usando el estadístico de prueba de la siguiente manera
Como caso especial de la prueba t de una muestra, la distribución nula del estadístico de prueba t pareada es una distribución t (con n — 1 grados de libertad), que es la distribución bajo la cual se calculan los valores p.
Dejaremos que el software encuentre el valor p para nosotros, y en este caso, nos da un valor p de 0.0183 (SAS) o 0.018 (SPSS).
El pequeño valor p nos dice que hay muy pocas posibilidades de obtener datos como los observados (o incluso más extremos) si la hipótesis nula fuera cierta. Más específicamente, hay menos de un 2% de probabilidad (0.018= 1.8%) de obtener un estadístico de prueba de -2.58 (o menor) o 2.58 (o superior), asumiendo que 2 cervezas no tienen impacto en los tiempos de reacción.
Paso 4: Conclusión
En nuestro ejemplo, el valor p es 0.018, lo que indica que los datos proporcionan suficiente evidencia para rechazar Ho.
- Conclusión: Existe suficiente evidencia de que beber dos cervezas se asocia con diferencias en los tiempos de reacción de los conductores.
Intervalo de confianza de seguimiento:
Como seguimiento a esta conclusión, cuantificamos el efecto que dos cervezas tienen sobre el conductor, utilizando el intervalo de confianza del 95% para μ d.
Utilizando software estadístico, encontramos que el intervalo de confianza del 95% para μ d, la media de las diferencias (antes — después), es aproximadamente (-0.9, -0.1).
Nota: Dado que las diferencias se calcularon antes y después, los tiempos de reacción más largos después de las cervezas se traducirían en diferencias negativas.
- Interpretación: Estamos 95% seguros de que después de tomar dos cervezas, el verdadero aumento medio en el tiempo total de reacción de los conductores es de entre 0.1 y 0.9 de segundo.
- Por lo tanto, los resultados del estudio sí indican deterioro de los conductores (tiempos de reacción más largos) ¡no al revés!
Dado que el intervalo de confianza no contiene el valor nulo de cero, podemos usarlo para decidir rechazar la hipótesis nula. Cero no es un valor plausible de la diferencia media poblacional basada en el intervalo de confianza. Observe que el uso de este método no siempre es práctico ya que a menudo todavía necesitamos proporcionar el valor p en la investigación clínica. (Nota: esta NO es la interpretación del intervalo de confianza sino un método de usar el intervalo de confianza para realizar una prueba de hipótesis.)
¿Conseguí esto? Intervalos de confianza para la diferencia media poblacional
(Versión no interactiva — Alerta de spoiler)
Importancia práctica:
Definitivamente deberíamos preguntarnos si esto es prácticamente significativo y yo diría que lo es.
- Aunque una diferencia en el tiempo medio de reacción de 0.1 segundos puede no ser tan mala, una diferencia de 0.9 segundos es probablemente un problema.
- Incluso con una diferencia en el tiempo de reacción de 0.4 segundos, si viajaras 60 millas por hora, esto se traduciría en una distancia recorrida de alrededor de 35 pies.
Muchos estudiantes se preguntan: Valores P unilaterales vs.
En la salida, generalmente se nos proporciona el valor p bilateral. Debemos tener mucho cuidado al convertir esto a un valor p unilateral (si no lo proporciona el software)
- SI los datos están en la dirección de nuestra hipótesis alternativa entonces simplemente podemos tomar la mitad del valor p bilateral.
- SI, sin embargo, los datos NO están en la dirección de la alternativa, el valor p correcto es MUY GRANDE y es el complemento de (uno menos) la mitad del valor p bilateral.
El ejemplo de “conducir después de tener 2 cervezas” es un caso en el que las observaciones se emparejan por tema. Es decir, ambas muestras tienen el mismo sujeto, de manera que cada sujeto se mide dos veces. Típicamente, como en nuestro ejemplo, una de las mediciones ocurre antes de un tratamiento/intervención (2 cervezas en nuestro caso), y la otra medición después del tratamiento/intervención.
Nuestro siguiente ejemplo es otro tipo de estudio típico donde se utiliza el diseño de pares emparejados, es un estudio que involucra gemelos.
EJEMPLO: Puntuaciones
Los investigadores han estado interesados desde hace mucho tiempo en la medida en que la inteligencia, medida por el puntaje de CI, se ve afectada por la “crianza” en lugar de la “naturaleza”: es decir, ¿los puntajes de CI de las personas son principalmente el resultado de su crianza y entorno, o son principalmente un rasgo heredado?
Se diseñó un estudio para medir el efecto del ambiente hogareño en la inteligencia, o más específicamente, el estudio fue diseñado para abordar la pregunta: “¿Existen diferencias estadísticamente significativas en los puntajes de CI entre las personas que fueron criadas por sus padres biológicos y las que fueron criadas por otra persona?”
Para poder responder a esta pregunta, los investigadores necesitaron obtener dos grupos de sujetos (uno de la población de personas que fueron criadas por sus padres biológicos, y otro de la población de personas que fueron criadas por otra persona) que sean lo más similares posible en todos los demás aspectos. En particular, dado que las diferencias genéticas también pueden afectar la inteligencia, los investigadores quisieron controlar por este factor de confusión.
Sabemos por nuestra discusión sobre el diseño del estudio (en la unidad Producing Data del curso) que una forma de controlar (al menos teóricamente) todos los factores de confusión es la aleatorización, aleatorizando a los sujetos a los diferentes grupos de tratamiento. En este caso, sin embargo, esto no es posible. Este es un estudio observacional; no se puede aleatorizar a los niños para que sean criados por sus padres biológicos o para que sean criados por otra persona. ¿De qué otra manera podemos eliminar el factor genética? Podemos realizar un “estudio gemelo”.
Debido a que los gemelos idénticos son genéticamente iguales, un buen diseño para obtener información para responder a esta pregunta sería comparar los puntajes de coeficiente intelectual para gemelos idénticos, uno de los cuales es criado por padres biológicos y el otro por otra persona. Tal diseño (pares emparejados) es una excelente manera de hacer una comparación entre individuos que solo difieren con respecto a la variable explicativa de interés (crianza) pero que son tan parecidos como posiblemente puedan ser en todos los demás aspectos importantes (inteligencia innata). Gemelos idénticos criados fueron estudiados por Susan Farber, quien publicó sus estudios en el libro “Gemelos idénticos criados aparte” (1981, Libros básicos).
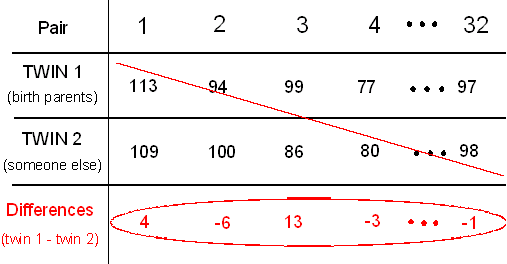
En este problema, vamos a utilizar los datos que aparecen en el libro de Farber en la tabla E6, de los puntajes de CI de 32 pares de gemelos idénticos que fueron criados separados.
Aquí hay una figura que te ayudará a entender este estudio:
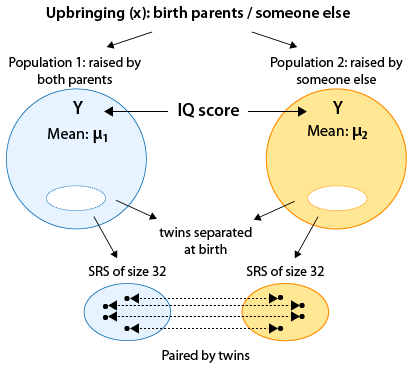
Estas son las cosas importantes a tener en cuenta en la figura:
- Esencialmente estamos comparando los puntajes medios de CI en dos poblaciones que se definen por nuestra variable explicativa (categórica de dos valores) — crianza (X), cuyos dos valores son: criado por padres biológicos, criado por otra persona.
- Este es un diseño de pares emparejados (a diferencia de un diseño de dos muestras independientes), ya que cada observación en una muestra está vinculada (emparejada) con una observación en la segunda muestra. Las observaciones son emparejadas por gemelos.
Cada una de las 32 filas representa un par de gemelos. Manteniendo la notación que usamos anteriormente, el gemelo 1 es el gemelo que fue criado por sus padres biológicos, y el gemelo 2 es el gemelo que fue criado por otra persona. Realicemos el análisis.
Paso 1: Indicar las hipótesis
Recordemos que en pares emparejados, reducimos los datos de dos muestras a una muestra de diferencias:
Las hipótesis se establecen en términos de la media de la diferencia donde, μ d = diferencia media poblacional en los puntajes de CI (Padres biológicos — Alguien más):
- Ho: μ d = 0 (indicando que la población de las diferencias se centra en un número que ES CERO)
- Ha: μ d ≠ 0 (indicando que la población de las diferencias se centra en un número que NO es CERO)
Paso 2: Obtener datos, verificar condiciones y resumir datos
¿Es seguro usar la prueba t pareada en este caso?
- Claramente, las muestras de gemelos no son muestras aleatorias de las dos poblaciones. No obstante, en este contexto, pueden considerarse como aleatorias, asumiendo que no hay nada especial en el coeficiente intelectual de una persona solo porque tiene un gemelo idéntico.
- El tamaño muestral aquí es n = 32. A pesar de que es el caso de que si usamos la regla general n > 30 nuestra muestra puede considerarse grande, es una especie de caso límite, así que solo para estar en el lado seguro, debemos mirar el histograma de las diferencias solo para asegurarnos de que no vemos nada extremo. (Comentario: Mirar el histograma de diferencias en cada caso es útil aunque la muestra sea muy grande, solo para tener una idea de los datos. Recordemos: “Siempre mira los datos”).
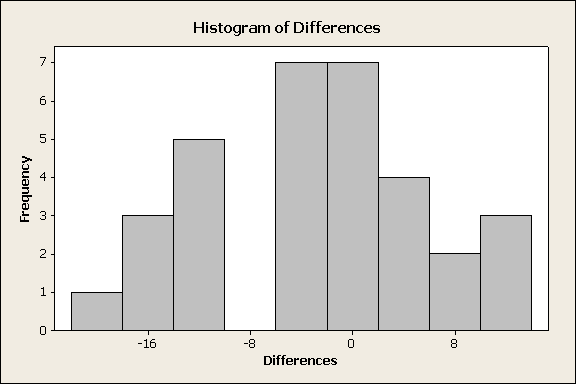
Los datos no revelan nada de lo que debamos preocuparnos (como asimetría muy extrema o valores atípicos), por lo que podemos proceder con seguridad. Al observar el histograma, observamos que la mayoría de las diferencias son negativas, lo que indica que en la mayoría de los 32 pares de gemelos, el gemelo 2 (levantado por otra persona) tiene un coeficiente intelectual más alto.
A partir de este punto nos apoyamos en el software estadístico, y encontramos que:
- valor t = -1.85
- valor p = 0.074
Nuestra estadística de prueba es -1.85.
Nuestros datos (representados por la media muestral de las diferencias) son 1.85 errores estándar por debajo de la hipótesis nula (representada por el valor nulo 0).
Paso 3: Encuentre el valor p de la prueba usando el estadístico de prueba de la siguiente manera
El valor p es de 0.074, lo que indica que existe una probabilidad de 7.4% de obtener datos como los observados (o incluso más extremos) asumiendo que H o es cierto (es decir, asumiendo que no hay diferencias en los puntajes de CI entre las personas que fueron criadas por sus padres naturales y las que no lo fueron).
Paso 4: Conclusión
Usando el nivel de significancia convencional (probabilidad de corte) de .05, nuestro valor p no es lo suficientemente pequeño y, por lo tanto, no podemos rechazar H o.
- Conclusión: Nuestros datos no proporcionan evidencia suficiente para concluir que si una persona fue criada por sus padres naturales tiene un impacto en la inteligencia de la persona (medida por puntajes de CI).
Intervalo de confianza:
El intervalo de confianza del 95% para la diferencia media poblacional es (-6.11322, 0.30072).
Interpretación:
- Estamos 95% seguros de que el coeficiente intelectual medio de la población para gemelos criados por otra persona es entre 6.11 mayor a 0.3 menor que el de los gemelos criados por sus padres biológicos.
- O... Estamos 95% seguros de que el coeficiente intelectual medio de la población para gemelos criados por sus padres biológicos es entre 6.11 menor a 0.3 mayor que el de los gemelos criados por otra persona.
- Nota: El orden de los grupos así como los números proporcionados en el intervalo pueden variar, lo importante es obtener el “inferior” y “mayor” con el valor correcto basado en el orden de grupo que se esté utilizando.
- Aquí usamos Padres biológicos — Alguien más y así un número positivo para nuestra población la diferencia media indica que el grupo de padres biológicos es mayor (alguien más gorup es menor) y un número negativo indica que el grupo de otra persona es mayor (el grupo de padres biológicos es menor).
Este intervalo de confianza sí contiene cero y por lo tanto da como resultado la misma conclusión a la prueba de hipótesis. Cero ES un valor plausible de la diferencia media poblacional y así no podemos rechazar la hipótesis nula.
Importancia práctica:
- El intervalo de confianza sí “se inclina” hacia que la diferencia sea negativa, lo que indica que en la mayoría de los 32 pares de gemelos, el gemelo 2 (levantado por otra persona) tiene un coeficiente intelectual más alto. La diferencia de medias muestrales es de -2.9 por lo que habría que considerar si este valor y rango de valores plausibles tienen alguna significación práctica real.
- En este caso, no creo que consideraría que una diferencia en el puntaje de CI de alrededor de 3 puntos sea muy importante en la práctica (pero otros podrían estar razonablemente en desacuerdo).
Es muy importante prestar atención a si la prueba t de dos muestras o la prueba t pareada es apropiada. Es decir, ser consciente del diseño del estudio es sumamente importante. Consideremos nuestro ejemplo, si no hubiéramos “capturado” que este es un diseño de pares emparejados, y hubiéramos analizado los datos como si las dos muestras fueran independientes usando la prueba t de dos muestras, habríamos obtenido un valor p de 0.114.
Tenga en cuenta que usando este método (incorrecto) para analizar los datos, y un nivel de significancia de 0.05, concluimos que los datos no proporcionan evidencia suficiente para concluir que los tiempos de reacción diferían después de beber dos cervezas. Este es un ejemplo de cómo usar el método estadístico incorrecto puede llevarte a conclusiones equivocadas, lo que en este contexto puede tener implicaciones muy graves.
Comentarios:
- El intervalo de confianza del 95% para μ se puede usar aquí de la misma manera que para las proporciones para realizar la prueba bilateral (comprobando si el valor nulo cae dentro o fuera del intervalo de confianza) o siguiendo una prueba t donde Ho fue rechazado para obtener una idea del valor de μ.
- En la mayoría de las situaciones en la práctica utilizamos pruebas de hipótesis de dos caras, seguidas de intervalos de confianza para obtener más información.
Ahora prueba un ejemplo completo por ti mismo.
Aprende haciendo: Pares emparejados — Datos de semillas de Gosset
(Versión no interactiva — Alerta de spoiler)
Datos adicionales para la práctica
Aquí hay otros dos conjuntos de datos con muestras emparejadas.
- Semillas: formato SPSS, formato SAS, formato Excel, formato CSV
- Gemelos: formato SPSS, formato SAS, formato Excel, formato CSV
Alternativas no paramétricas para datos de pares coincidentes
Objetivos de aprendizaje
LO 5.1: Para una situación de análisis de datos que involucre dos variables, determinar el método alternativo apropiado (no paramétrico) cuando no se cumplan los supuestos de nuestros métodos estándar.
Las pruebas estadísticas que hemos discutido previamente (y muchas las discutiremos) requieren suposiciones sobre la distribución en la población o sobre los requisitos para utilizar una cierta aproximación como distribución muestral. Estos métodos se denominan paramétricos.
Cuando estos supuestos no son válidos, a menudo existen métodos alternativos para probar hipótesis similares. Las pruebas que requieren solo suposiciones distribucionales mínimas, si las hay, se denominan pruebas no paramétricas o libres de distribución.
Al final de esta sección proporcionaremos algunos detalles (ver Detalles para Alternativas No Paramétricas), por ahora simplemente queremos mencionar que existen dos alternativas no paramétricas comunes a la prueba t pareada. Ellos son:
- Prueba de Signo
- Prueba de rango ED de signo Wilcoxon
El hecho de que ambas pruebas tengan la palabra “signo” en ellas no es una coincidencia —se debe a que nos interesará si las diferencias tienen un signo positivo o un signo negativo— y el hecho de que esta palabra aparezca en ambas pruebas puede ayudar que recuerdes que corresponden a métodos pareados donde a menudo nos interesa si hubo un aumento (signo positivo) o una disminución (signo negativo).
Resumimos
- La prueba t pareada se utiliza para comparar dos medias poblacionales cuando las dos muestras (extraídas de las dos poblaciones) son dependientes en el sentido de que cada observación en una muestra puede vincularse a una observación en la otra muestra. Tal diseño se llama “pares emparejados”.
- El caso más común en el que se utiliza el diseño de pares emparejados es cuando los mismos sujetos se miden dos veces, generalmente antes y luego después de algún tipo de tratamiento y/o intervención. Otro caso clásico son los estudios que involucran a gemelos.
- En el fondo, tenemos un explicativo categórico de dos valores cuyas categorías definen las dos poblaciones que estamos comparando y cuyo efecto en la variable de respuesta que estamos tratando de evaluar.
- La idea detrás de la prueba t pareada es reducir los datos de dos muestras a una sola muestra de las diferencias, y usar estas diferencias observadas como datos para la inferencia sobre una sola media, la media de las diferencias, μ d.
- Por lo tanto, la prueba t pareada es simplemente una prueba t de una muestra para la media de las diferencias μ d, donde el valor nulo es 0.
- Una vez que verifiquemos que podemos proceder con seguridad con la prueba t emparejada, utilizamos la salida del software para llevarla a cabo.
- Un intervalo de confianza del 95% para μ d puede ser muy perspicaz después de que una prueba haya rechazado la hipótesis nula, y también se puede usar para pruebas en el caso bilateral.
- Dos alternativas no paramétricas a la prueba t pareada son la prueba de signos y la prueba de Wilcoxon signed — rank test. (Ver Detalles para Alternativas No Paramétricas.)
Dos Muestras Independientes
CO-4: Distinguir entre diferentes escalas de medición, elegir los métodos estadísticos descriptivos e inferenciales adecuados basados en estas distinciones e interpretar los resultados
Objetivos de aprendizaje
LO 4.35: Para una situación de análisis de datos que involucre dos variables, elija el método inferencial apropiado para examinar la relación entre las variables y justificar la elección.
Objetivos de aprendizaje
LO 4.36: Para una situación de análisis de datos que involucre dos variables, llevar a cabo el método inferencial apropiado para examinar las relaciones entre las variables y sacar las conclusiones correctas en contexto.
CO-5: Determinar alternativas metodológicas preferidas a los métodos estadísticos de uso común cuando no se cumplen los supuestos.
REVISIÓN: Unidad 1 Caso C-Q
Video
Video: Dos muestras independientes (38:56)
Tutoriales SAS relacionados
- 7A (2:32) Resúmenes numéricos por grupos
- 7B (3:03) Parcelas de caja lado a lado
- 7C (6:57) Prueba T de Dos Muestras
Tutoriales relacionados con SPSS
- 7A (3:29) Resúmenes numéricos por grupos
- 7B (1:59) Parcelas de caja lado a lado
- 7C (5:30) Prueba T de Dos Muestras
Introducción
Aquí un resumen de las pruebas que aprenderemos para el escenario donde k = 2. Los métodos en BOLD serán nuestro foco principal.
Hemos completado nuestra discusión sobre muestras dependientes (2da columna) y ahora pasamos a muestras independientes (1ª columna).
Muestras independientes (más énfasis) |
Muestras Dependientes (Menos Énfasis) |
Pruebas estándar
Prueba no paramétrica
|
Prueba estándar
Pruebas no paramétricas
|
Muestras dependientes vs. independientes
Objetivos de aprendizaje
LO 4.37: Identificar y distinguir entre muestras independientes y dependientes.
Se discutió el caso muestral dependiente donde las observaciones son coincidentas/emparejadas/enlazadas entre las dos muestras. Recordemos que en ese escenario las observaciones pueden ser del mismo individuo o dos individuos que se emparejan entre muestras. Para analizar datos de muestras dependientes, simplemente tomamos las diferencias y analizamos la diferencia usando técnicas de una muestra.
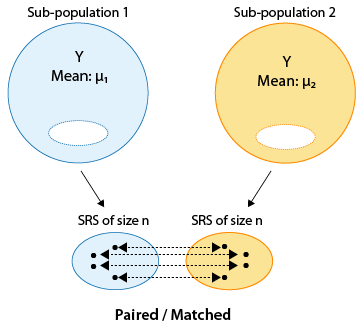
Ahora discutiremos el caso de muestra independiente. En este caso, todos los individuos son independientes de todos los demás individuos de su muestra así como de todos los individuos de la otra muestra. Esto se logra con mayor frecuencia por cualquiera de los siguientes:
- Tomando una muestra aleatoria de cada uno de los dos grupos en estudio. Por ejemplo, para comparar alturas de machos y hembras, podríamos tomar una muestra aleatoria de 100 hembras y otra muestra aleatoria de 100 machos. El resultado serían dos muestras que son independientes entre sí.
- Tomar una muestra aleatoria de toda la población y luego dividirla en dos submuestras con base en la variable de agrupación de interés. Por ejemplo, tomamos una muestra aleatoria de adultos estadounidenses y luego los dividimos en dos muestras según el género. Esto da como resultado una submuestra de hembras y una submuestra de machos que son independientes entre sí.
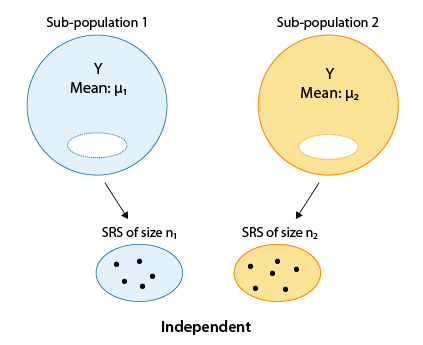
Comparación de dos medias: prueba T de dos muestras independientes
Objetivos de aprendizaje
LO 4.38: En un contexto dado, determinar el método estándar apropiado para comparar grupos y proporcionar las conclusiones correctas dado el resultado del software apropiado.
Objetivos de aprendizaje
LO 4.39: En un contexto dado, establecer las hipótesis nulas y alternativas apropiadas para comparar grupos.
Recordemos que aquí nos interesa el efecto de una variable categórica de dos valores (k = 2) (X) sobre una respuesta cuantitativa (Y). Se obtienen muestras aleatorias de las dos subpoblaciones (definidas por las dos categorías de X) y necesitamos evaluar si los datos proporcionan o no suficiente evidencia para creer que las dos medias de la subpoblación son diferentes.
Es decir, nuestro objetivo es probar si las medias μ 1 y μ 2 (que son las medias de la variable de interés en las dos subpoblaciones) son iguales o no, y para ello tenemos dos muestras, una de cada subpoblación, las cuales fueron elegidas independientemente entre sí.
La prueba que aprenderemos aquí se conoce comúnmente como la prueba t de dos muestras. Como su nombre indica, se trata de una prueba t, que como sabemos significa que los valores p para esta prueba se calculan bajo alguna distribución t.
Aquí hay cifras que ilustran algunos de los ejemplos que cubriremos. Observe cómo se representan las variables originales X (variable categórica con dos niveles) e Y (variable cuantitativa). Piensa en el hecho de que estamos en el caso C → Q!
Al igual que en nuestra discusión de muestras dependientes, a menudo simplificaremos nuestra terminología y simplemente usaremos los términos “población 1” y “población 2” en lugar de referirnos a estas como subpoblaciones. Cualquiera de las dos terminología está bien.
Muchos estudiantes se preguntan: dos muestras independientes
Pregunta: ¿Importa qué población etiquetamos como población 1 y cuál como población 2?
Respuesta: No, no importa siempre y cuando seas consistente, es decir, que no cambies etiquetas en el medio.
- PERO... considerar cómo se etiquetan las poblaciones es importante para exponer las hipótesis y en la interpretación de los resultados.
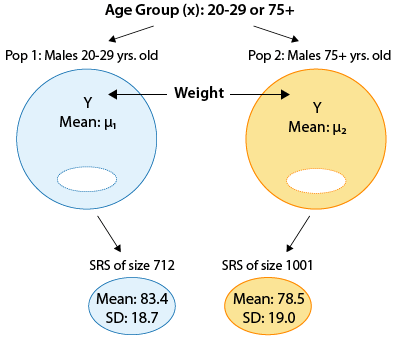
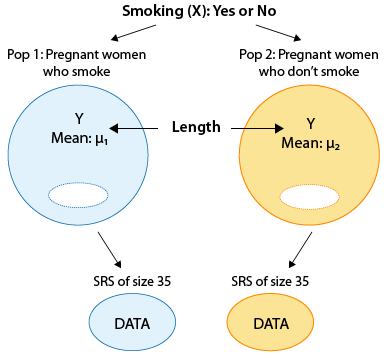
Pasos para la prueba T de dos muestras
Recordemos que nuestro objetivo es comparar las medias μ 1 y μ 2 con base en las dos muestras independientes.
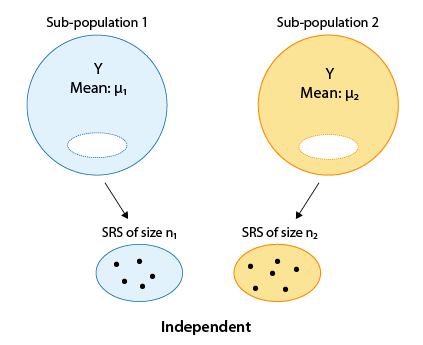
- Paso 1: Indicar las hipótesis
Las hipótesis representan nuestro objetivo de comparar μ 1 y μ 2.
La hipótesis nula es siempre:
Ho: μ 1 — μ 2 = 0 (que es lo mismo que μ 1 = μ 2)
(NO HAY asociación entre la variable explicativa categórica y la variable de respuesta cuantitativa)
Nos centraremos en la hipótesis alternativa bilateral de la forma:
Ha: μ 1 — μ 2 ≠ 0 (que es lo mismo que μ 1 ≠ μ 2) (bilateral)
(HAY UNA asociación entre la variable explicativa categórica y la variable de respuesta cuantitativa)
Obsérvese que la hipótesis nula afirma que no hay diferencia entre las medias. Conceptualmente, Ho afirma que no existe relación entre las dos variables relevantes (X e Y).
Nuestro parámetro de interés en este caso (el parámetro sobre el que estamos haciendo una inferencia) es la diferencia entre las medias (μ 1 — μ 2) y el valor nulo es 0. La hipótesis alternativa afirma que existe una diferencia entre las medias.
¿Conseguí esto? ¿Qué significan nuestras hipótesis en contexto?
(Versión no interactiva — Alerta de spoiler)
- Paso 2: Obtener datos, verificar condiciones y resumir datos
La prueba t de dos muestras se puede utilizar de forma segura siempre que se cumplan las siguientes condiciones:
Las dos muestras son, en efecto, independientes.
Nos encontramos en uno de los dos escenarios siguientes:
(i) Ambas poblaciones son normales, o más específicamente, la distribución de la respuesta Y en ambas poblaciones es normal, y ambas muestras son aleatorias (o al menos pueden considerarse como tales). En la práctica, verificar la normalidad en las poblaciones se realiza observando cada una de las muestras mediante un histograma y comprobando si hay algún signo de que las poblaciones no son normales. Tales signos podrían ser asimetría extrema y/o valores atípicos extremos.
(ii) Se sabe o se descubre que las poblaciones no son normales, pero el tamaño muestral de cada una de las muestras aleatorias es suficientemente grande (podemos usar la regla general de que un tamaño de muestra mayor a 30 se considera suficientemente grande).
¿Conseguí esto? Condiciones para dos muestras independientes
(versión no interactiva — alerta de spoiler)
Suponiendo que podemos usar con seguridad la prueba t de dos muestras, necesitamos resumir los datos, y en particular, calcular nuestro resumen de datos: el estadístico de prueba.
Estadística de prueba para la prueba T de dos muestras:
Hay dos opciones para nuestra estadística de prueba, y debemos elegir la adecuada para resumir nuestros datos Veremos cómo elegir entre las dos estadísticas de prueba en la siguiente sección. Las dos opciones son las siguientes:
Utilizamos la siguiente notación para describir nuestras muestras:
\(n_1, n_2\)= tamaños de muestra de las muestras de población 1 y población 2
\(\bar{y}_1, \bar{y}_2\)= medias muestrales de las muestras de población 1 y población 2
\(s_1, s_2\)= desviaciones estándar muestrales de las muestras de la población 1 y la población 2
\(s_p\)= estimación agrupada de una desviación estándar de población común
Aquí están los dos casos para nuestro estadístico de prueba.
(A) Varianzas iguales: Si es seguro suponer que las dos poblaciones tienen desviaciones estándar iguales, podemos agrupar nuestras estimaciones de esta desviación estándar poblacional común y utilizar el siguiente estadístico de prueba.
\(t=\dfrac{\bar{y}_{1}-\bar{y}_{2}-0}{s_{p} \sqrt{\frac{1}{n_{1}}+\frac{1}{n_{2}}}}\)
donde
\(s_{p}=\sqrt{\dfrac{\left(n_{1}-1\right) s_{1}^{2}+\left(n_{2}-1\right) s_{2}^{2}}{n_{1}+n_{2}-2}}\)
(B) Varianzas Desiguales: Si NO es seguro asumir que las dos poblaciones tienen desviaciones estándar iguales, tenemos desviaciones estándar desiguales y debemos usar el siguiente estadístico de prueba.
\(t=\dfrac{\bar{y}_{1}-\bar{y}_{2}-0}{\sqrt{\frac{s_{1}^{2}}{n_{1}}+\frac{s_{2}^{2}}{n_{2}}}}\)
Comentarios:
- Es posible nunca asumir varianzas iguales; sin embargo, si se cumple el supuesto de varianzas iguales, la prueba t de varianzas iguales tendrá mayor poder para detectar la diferencia de interés.
- No estaremos calculando los valores de estas estadísticas de prueba a mano en este curso. En cambio, confiaremos en el software para obtener el valor para nosotros.
- Ambos estadísticos de prueba miden (en errores estándar) qué tan lejos están nuestros datos (representados por la diferencia de las medias de la muestra) de la hipótesis nula (representada por el valor nulo, 0).
- Estas estadísticas de prueba tienen la misma forma general que otras que hemos comentado. No discutiremos la derivación de los errores estándar en cada caso pero se debe entender esta forma general y poder identificar cada componente para un estadístico de prueba específico.
\(\text{test statistic} = \dfrac{\text{estimator - null value}}{\text{standard error of estimator}}\)
- Paso 3: Encuentre el valor p de la prueba usando el estadístico de prueba de la siguiente manera
Cada una de estas pruebas se basa en una distribución t particular bajo la cual se calculan los valores p. En el caso de que se asuman varianzas iguales, los grados de libertad son simplemente:
\(n_1 + n_2 - 2\)
mientras que en el caso de las varianzas desiguales, la fórmula para los grados de libertad es más compleja. Confiaremos en el software para obtener los grados de libertad en ambos casos y nos proporcionó el valor p correcto (generalmente este será un valor p bilateral).
- Paso 4: Conclusión
Como es habitual, sacamos nuestra conclusión con base en el valor p. Asegúrese de escribir sus conclusiones en contexto especificando sus variables actuales y/o describiendo con precisión la diferencia en las medias de población en términos de las variables actuales.
Si el valor p es pequeño, existe una diferencia estadísticamente significativa entre lo observado en la muestra y lo que se reclamó en Ho, por lo que rechazamos Ho.
Conclusión: Existe suficiente evidencia de que la variable explicativa categórica está relacionada con (o asociada con) la variable de respuesta cuantitativa. Más específicamente, hay suficiente evidencia de que la diferencia en medias poblacionales no es igual a cero.
Si el valor p no es pequeño, no tenemos evidencia estadística suficiente para rechazar a Ho.
Conclusión: NO hay evidencia suficiente de que la variable explicativa categórica esté relacionada con (o asociada con) la variable de respuesta cuantitativa. Más específicamente, hay suficiente evidencia de que la diferencia en medias poblacionales no es igual a cero.
En particular, si se especifica una probabilidad de corte, α (nivel de significancia), rechazamos Ho si el valor p es menor que α. De lo contrario, no rechazamos a Ho.
Objetivos de aprendizaje
LO 4.41: Con base en el resultado de una prueba t de dos muestras, interpretar correctamente en contexto el intervalo de confianza apropiado para la diferencia entre medias poblacionales
Como en métodos anteriores, podemos hacer un seguimiento con un intervalo de confianza para la diferencia entre medias poblacionales, μ 1 — μ 2 e interpretar este intervalo en el contexto del problema.
Interpretación: Estamos 95% seguros de que la media poblacional para (un grupo) está entre __________________ en comparación con la media poblacional para (el otro grupo).
Los intervalos de confianza también se pueden usar para determinar si rechazar o no la hipótesis nula de la prueba en función de si el valor nulo de cero cae o no fuera del intervalo o dentro.
Si el valor nulo, 0, cae fuera del intervalo de confianza, Ho es rechazado. (Cero NO es un valor plausible basado en el intervalo de confianza)
Si el valor nulo, 0, cae dentro del intervalo de confianza, Ho no es rechazado. (Cero ES un valor plausible basado en el intervalo de confianza)
NOTA: Tenga cuidado de elegir el intervalo de confianza correcto sobre la diferencia entre medias poblacionales usando el mismo supuesto (varianzas iguales o varianzas desiguales) y no los intervalos de confianza individuales para las medias en los propios grupos.
Muchos estudiantes se preguntan: resultados de software estadístico de lectura para la prueba T de dos muestras
Prueba de Igualdad de Varianzas (o Desviaciones Estándar)
Objetivos de aprendizaje
LO 4.42: Con base en la salida para una prueba t de dos muestras, determinar si usar los resultados asumiendo varianzas iguales o aquellos asumiendo varianzas desiguales.
Dado que tenemos dos pruebas posibles que podemos realizar, con base en si podemos suponer o no que las desviaciones estándar de la población (o varianzas) son iguales, necesitamos un método para determinar qué prueba usar.
Aunque puedes hacer una conjetura razonable usando información de los datos (es decir, mirar las distribuciones y estimaciones de las desviaciones estándar y ver si sientes que son razonablemente iguales), tenemos una prueba que puede ayudarnos aquí, llamada prueba de Igualdad de Varianzas. Esta salida se muestra automáticamente en muchos paquetes de software cuando se solicita una prueba t de dos muestras aunque la prueba particular utilizada puede variar. Las hipótesis de esta prueba son:
Ho: σ 1 = σ 2 (las desviaciones estándar en las dos poblaciones son las mismas)
Ha: σ 1 ≠ σ 2 (las desviaciones estándar en las dos poblaciones no son las mismas)
- Si el valor p de esta prueba para varianzas iguales es pequeño, hay suficiente evidencia de que las desviaciones estándar en las dos poblaciones son diferentes y no podemos asumir varianzas iguales.
- IMPORTANTE! En este caso, cuando realizamos la prueba t de dos muestras para comparar las medias poblacionales, utilizamos el estadístico de prueba para varianzas desiguales.
- Si el valor p de esta prueba es grande, no hay evidencia suficiente de que las desviaciones estándar en las dos poblaciones sean diferentes. En este caso asumiremos varianzas iguales ya que no tenemos pruebas claras de lo contrario.
- IMPORTANTE! En este caso, cuando realizamos la prueba t de dos muestras para comparar las medias poblacionales, utilizamos el estadístico de prueba para varianzas iguales.
Ahora veamos un ejemplo completo de realización de una prueba t de dos muestras, incluida la prueba incrustada para la igualdad de varianzas.
EJEMPLO: ¿Qué es más importante, personalidad o apariencia?
Esta pregunta se hizo a una muestra aleatoria de 239 estudiantes universitarios, quienes debían responder en una escala del 1 al 25. Una respuesta de 1 significa que la personalidad tiene la máxima importancia y no parece ninguna importancia en absoluto, mientras que una respuesta de 25 significa que las miradas tienen la máxima importancia y la personalidad no tiene importancia en absoluto. El propósito de esta encuesta fue examinar si los hombres y las mujeres difieren con respecto a la importancia de la apariencia vs. personalidad.
Tenga en cuenta que los datos tienen el siguiente formato:
| Puntuación (Y) | Género (X) |
|---|---|
| 15 | Macho |
| 13 | Hembra |
| 10 | Hembra |
| 12 | Macho |
| 14 | Hembra |
| 14 | Macho |
| 6 | Macho |
| 17 | Macho |
| etc. |
El formato de los datos nos recuerda que esencialmente estamos examinando la relación entre la variable categórica de dos valores, género, y la respuesta cuantitativa, score. Los dos valores de la variable explicativa categórica (k = 2) definen las dos poblaciones que estamos comparando: machos y hembras. La comparación es con respecto a la puntuación de la variable de respuesta. Aquí hay una figura que resume el ejemplo:
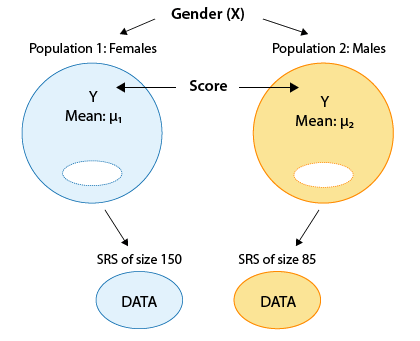
Comentarios:
- Obsérvese que esta cifra enfatiza cómo el hecho de que nuestro explicativo sea una variable categórica de dos valores significa que en la práctica estamos comparando dos poblaciones (definidas por estos dos valores) con respecto a nuestra respuesta Y.
- Tenga en cuenta que a pesar de que la descripción del problema solo dice que tuvimos 239 estudiantes, la cifra nos dice que había 85 machos en la muestra, y 150 hembras.
- Dando seguimiento al comentario 2, tenga en cuenta que 85 + 150 = 235 y no 239. En estos datos (que son reales) hay cuatro “observaciones faltantes”, 4 estudiantes para los cuales no tenemos el valor de la variable respuesta, “importancia”. Esto podría deberse a una serie de razones, como error de grabación o falta de respuesta. La conclusión es que a pesar de que se recolectaron datos de 239 estudiantes, efectivamente tenemos datos de solo 235. (Recomendado: Pasar por el archivo de datos y señalar que hay 4 casos de observaciones faltantes: estudiantes 34, 138, 179, y 183).
Paso 1: Indicar las hipótesis
Recordemos que el propósito de esta encuesta fue examinar si las opiniones de mujeres y hombres difieren con respecto a la importancia de la apariencia vs. personalidad. Por lo tanto, las hipótesis en este caso son:
Ho: μ 1 — μ 2 = 0 (que es lo mismo que μ 1 = μ 2)
Ha: μ 1 — μ 2 ≠ 0 (que es lo mismo que μ 1 ≠ μ 2)
donde μ 1 representa la media “apariencia vs puntuación de personalidad” para las mujeres y μ 2 representa la media “apariencia vs puntuación de personalidad” para los hombres.
Es importante entender que conceptualmente, las dos hipótesis afirman:
Ho: La puntuación (de looks vs. personalidad) no está relacionada con el género
Ja: La puntuación (de looks vs. personalidad) está relacionada con el género
Paso 2: Obtener datos, verificar condiciones y resumir datos
- Datos: Parece formato SPSS, formato SAS, formato Excel, formato CSV
- Primero comprobemos si se cumplen las condiciones que nos permiten usar de manera segura la prueba t de dos muestras.
- Aquí se eligieron 239 estudiantes que se dividieron de forma natural en una muestra de hembras y una muestra de machos. Dado que los estudiantes fueron elegidos al azar, la muestra de hembras es independiente de la muestra de machos.
- Aquí estamos en el segundo escenario —los tamaños de muestra (150 y 85), son definitivamente lo suficientemente grandes, y así podemos proceder independientemente de que las poblaciones sean normales o no.
- En la salida a continuación analizamos primero la prueba de igualdad de varianzas (delineada en naranja). Los resultados de la prueba t de dos muestras que usaremos están delineados en azul.
- Hay DOS PRUEBAS representadas en esta salida y debemos tomar la decisión correcta para que AMBAS de estas pruebas procedan correctamente.
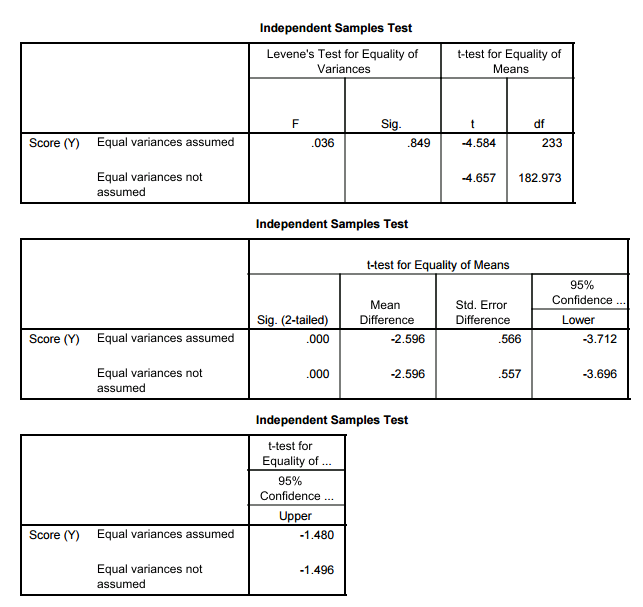
- SALIDA SOFTWARE En SPSS
- El valor p para la prueba de igualdad de varianzas se reporta como 0.849 en la columna SIG bajo la prueba de Levene para igualdad de varianzas. (Tenga en cuenta que esto difiere del valor p encontrado usando SAS, dos pruebas diferentes se utilizan por defecto entre los dos programas).
- Por lo que no podemos rechazar la hipótesis nula de que las varianzas, o equivalentemente las desviaciones estándar, son iguales (Ho: σ 1 = σ 2).
- Conclusión para probar la igualdad de varianzas: No podemos concluir que haya una diferencia en la varianza de apariencia vs. puntaje de personalidad entre hombres y mujeres.
- Esto da como resultado el uso de la fila para Varianzas iguales asumidas para encontrar los resultados de la prueba t incluyendo el estadístico de prueba, el valor p y el intervalo de confianza para la diferencia. (Delineado en AZUL)

La salida también podría dividirse si exporta o copia los elementos de ciertas maneras. Los resultados son los mismos pero puede ser más difícil de leer.
- SALIDA SOFTWARE En SAS:
- El valor p para la prueba de igualdad de varianzas se reporta como 0.5698 en la columna Pr > F bajo igualdad de varianzas. (Tenga en cuenta que esto difiere del valor p encontrado usando SPSS, dos pruebas diferentes se utilizan por defecto entre los dos programas).
- Por lo que no podemos rechazar la hipótesis nula de que las varianzas, o equivalentemente las desviaciones estándar, son iguales (Ho: σ 1 = σ 2).
- Conclusión para probar la igualdad de varianzas: No podemos concluir que haya una diferencia en la varianza de apariencia vs. puntaje de personalidad entre hombres y mujeres.
- Esto da como resultado el uso de la fila para el método POOLED donde se asumen varianzas iguales para encontrar los resultados de la prueba t incluyendo el estadístico de prueba, el valor p y el intervalo de confianza para la diferencia. (Delineado en AZUL)
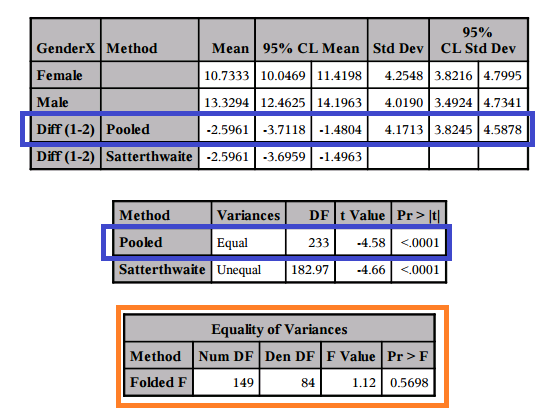
- ESTADÍSTICO DE PRUEBA para Prueba T de Dos Muestras: En todos los resultados anteriores, determinamos que usaremos la prueba que asume que las varianzas son IGUALES, y encontramos nuestro estadístico de prueba de t = -4.58.
Paso 3: Encuentre el valor p de la prueba usando el estadístico de prueba de la siguiente manera
- Vamos a dejar que el software encuentre el valor p para nosotros, y en este caso, el valor p es menor que nuestro nivel de significancia de 0.05 de hecho es prácticamente 0.
- Esto se encuentra en SPSS en las varianzas iguales asumidas fila bajo prueba t en el SIG. (de dos colas) dada como 0.000 y en SAS en la FILA agrupada bajo la columna Pr > |t| dada como <0.0001.
- Un valor p que es prácticamente 0 significa que sería casi imposible obtener datos como los observados (o incluso más extremos) si la hipótesis nula hubiera sido cierta.
- Más específicamente, en nuestro ejemplo, si no hubiera diferencias entre hembras y machos con respecto a si valoran la apariencia vs. personalidad, sería casi imposible (probabilidad aproximadamente 0) obtener datos donde la diferencia entre las medias muestrales de hembras y machos sea de -2.6 (esa diferencia es 10.73 — 13.33 = -2.6) o más extremos.
- Comentario: Tenga en cuenta que la salida nos dice que la diferencia μ 1 — μ 2 es aproximadamente -2.6. Pero lo más importante, queremos saber si esta diferencia es estadísticamente significativa. Para responder a esto, utilizamos el hecho de que esta diferencia es de 4.58 errores estándar por debajo del valor nulo.
Paso 4: Conclusión
Como de costumbre, un pequeño valor p aporta pruebas contra Ho. En nuestro caso nuestro valor p es prácticamente 0 (que es menor que cualquier nivel de significación que elijamos). Por lo tanto, los datos proporcionan pruebas muy fuertes contra Ho por lo que los rechazamos.
- Conclusión: Existe suficiente evidencia de que la puntuación media de Importancia (de apariencia vs personalidad) de los machos difiere de la de las hembras. En otras palabras, los machos y las hembras difieren con respecto a cómo valoran la apariencia vs. la personalidad.
Como seguimiento a esta conclusión, podemos construir un intervalo de confianza para la diferencia entre medias poblacionales. En este caso construiremos un intervalo de confianza para μ 1 — μ 2 la población media “looks vs puntaje de personalidad” para las mujeres menos la media de la población “looks vs puntaje de personalidad” para los hombres.
- Usando software estadístico, encontramos que el intervalo de confianza del 95% para μ 1 — μ 2 es aproximadamente (-3.7, -1.5).
- Esto se encuentra en SPSS en la fila asumida de varianzas iguales bajo columnas de intervalo de confianza del 95% dadas como -3.712 a -1.480 y en SAS en la fila agrupada bajo columna de 95% CL MEAN dada como -3.7118 a -1.4804 (tenga cuidado de NO elegir el intervalo de confianza para la desviación estándar en la última columna, 9% CL Std Dev).
- Interpretación:
- Estamos 95% seguros de que la media poblacional “apariencia vs puntaje de personalidad” para las mujeres es entre 3.7 y 1.5 puntos menor que la de los machos.
- O
- Estamos 95% seguros de que la media poblacional “apariencia vs puntaje de personalidad” para los hombres es entre 3.7 y 1.5 puntos mayor que la de las hembras.
- Por lo tanto, el intervalo de confianza cuantifica el efecto que la variable explicativa (género) tiene sobre la respuesta (looks vs puntaje de personalidad).
- Dado que los valores bajos corresponden a que la personalidad sea más importante y los valores altos corresponden a la apariencia siendo más importante, el resultado de nuestra investigación sugiere que, en promedio, las mujeres colocan la personalidad más alta que los machos. Alternativamente podríamos decir que el lugar de los machos se ve más alto que lo hacen las hembras.
- Nota: El intervalo de confianza no contiene cero (ambos valores son negativos en base a cómo elegimos nuestros grupos) y así usando el intervalo de confianza podemos rechazar la hipótesis nula aquí.
Importancia práctica:
Definitivamente deberíamos preguntarnos si esto es prácticamente significativo
- ¿Es significativa aquí una verdadera diferencia en las medias poblacionales representadas por nuestra estimación a partir de estos datos? Te dejaré considerar y responder por ti mismo.
Salida SPSS para este ejemplo (Salida no paramétrica para los Ejemplos 1 y 2)
Salida SAS y código SAS (incluye prueba no paramétrica)
Aquí hay otro ejemplo.
EJEMPLO: IMC vs. género en pacientes con ataque cardíaco
Se realizó un estudio que incluyó y siguió a pacientes con ataque cardíaco en cierta área metropolitana. En este ejemplo nos interesa determinar si existe una relación entre el Índice de Masa Corporal (IMC) y el género. Los individuos que se presentaron al hospital con un ataque cardíaco fueron seleccionados al azar para participar en el estudio.
Paso 1: Indicar las hipótesis
Ho: μ 1 — μ 2 = 0 (que es lo mismo que μ 1 = μ 2)
Ha: μ 1 — μ 2 ≠ 0 (que es lo mismo que μ 1 ≠ μ 2)
donde μ 1 representa el IMC medio para los machos y μ 2 representa el IMC medio para las hembras.
Es importante entender que conceptualmente, las dos hipótesis afirman:
Ho: El IMC no está relacionado con el género en pacientes con ataque cardíaco
Ha: El IMC está relacionado con el género en pacientes con ataque cardíaco
Paso 2: Obtener datos, verificar condiciones y resumir datos
- Datos: formato WHAS500 SPSS, formato SAS
- Primero comprobemos si se cumplen las condiciones que nos permiten usar de manera segura la prueba t de dos muestras.
- Aquí se escogieron sujetos y se dividieron naturalmente en una muestra de hembras y una muestra de machos. Dado que los sujetos fueron elegidos al azar, la muestra de hembras es independiente de la muestra de machos.
- Aquí, estamos en el segundo escenario —los tamaños muestrales son extremadamente grandes, por lo que podemos proceder independientemente de que las poblaciones sean normales o no.
- En la salida a continuación analizamos primero la prueba de igualdad de varianzas (delineada en naranja). Los resultados de la prueba t de dos muestras que usaremos están delineados en azul.
- Hay DOS PRUEBAS representadas en esta salida y debemos tomar la decisión correcta para que AMBAS de estas pruebas procedan correctamente.
- SALIDA SOFTWARE En SPSS
- El valor p para la prueba de igualdad de varianzas se reporta como 0.001 en la columna SIG bajo la prueba de Levene para igualdad de varianzas.
- Entonces rechazamos la hipótesis nula de que las varianzas, o equivalentemente las desviaciones estándar, son iguales (Ho: σ 1 = σ 2).
- Conclusión para probar la igualdad de varianzas: Concluimos que hay suficiente evidencia de una diferencia en la varianza de apariencia vs. puntaje de personalidad entre hombres y mujeres.
- Esto da como resultado el uso de la fila para Varianzas iguales NO asumidas para encontrar los resultados de la prueba t incluyendo el estadístico de prueba, el valor p y el intervalo de confianza para la diferencia. (Delineado en AZUL)

- SALIDA SOFTWARE En SAS:
- El valor p para la prueba de igualdad de varianzas se reporta como 0.0004 en la columna Pr > F bajo igualdad de varianzas.
- Entonces rechazamos la hipótesis nula de que las varianzas, o equivalentemente las desviaciones estándar, son iguales (Ho: σ 1 = σ 2).
- Conclusión para probar la igualdad de varianzas: Concluimos que hay suficiente evidencia de una diferencia en la varianza de apariencia vs. puntaje de personalidad entre hombres y mujeres.
- Esto da como resultado el uso de la fila para el método SATTERTHWAITE donde se asumen varianzas desiguales para encontrar los resultados de la prueba t incluyendo el estadístico de prueba, el valor p y el intervalo de confianza para la diferencia. (Delineado en AZUL)
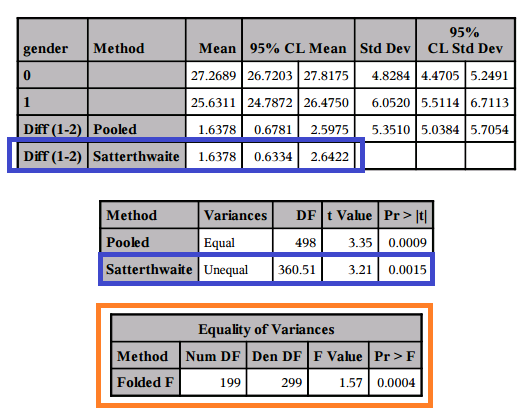
- ESTADÍSTICO DE PRUEBA para Prueba T de Dos Muestras: En todos los resultados anteriores, determinamos que usaremos la prueba que asume que las varianzas son DESIGUALES, y encontramos nuestro estadístico de prueba de t = 3.21.
Paso 3: Encuentre el valor p de la prueba usando el estadístico de prueba de la siguiente manera
- Dejaremos que el software encuentre el valor p para nosotros, y en este caso, el valor p es menor que nuestro nivel de significación de 0.05.
- Esto se encuentra en SPSS en las varianzas desiguales asumidas fila bajo prueba t en el SIG. (de dos colas) dada como 0.001 y en SAS en la FILA SATTERTHWAITE bajo la columna Pr > |t| dada como 0.0015.
- Este valor p significa que sería extremadamente raro obtener datos como los observados (o incluso más extremos) si la hipótesis nula hubiera sido cierta.
- Más específicamente, en nuestro ejemplo, si no existieran diferencias entre hembras y machos con respecto al IMC, sería casi altamente improbable (probabilidad 0.001) obtener datos donde la diferencia entre el IMC medio muestral de machos y hembras sea de 1.64 o más extremo.
- Comentario: Tenga en cuenta que la salida nos dice que la diferencia μ 1 — μ 2 es aproximadamente 1.64. Pero lo más importante, queremos saber si esta diferencia es estadísticamente significativa. Para responder a esto, utilizamos el hecho de que esta diferencia es de 3.21 errores estándar por encima del valor nulo.
Paso 4: Conclusión
Como de costumbre, un pequeño valor p aporta pruebas contra Ho. En nuestro caso nuestro valor p es 0.001 (que es menor que cualquier nivel de significación que elegiremos). Por lo tanto, los datos proporcionan pruebas muy fuertes contra Ho por lo que los rechazamos.
- Conclusión: El IMC medio de los machos difiere del de las hembras. En otras palabras, hombres y mujeres difieren con respecto al IMC entre los pacientes con ataque cardíaco.
Como seguimiento a esta conclusión, podemos construir un intervalo de confianza para la diferencia entre medias poblacionales. En este caso construiremos un intervalo de confianza para μ 1 — μ 2 el IMC medio poblacional para los varones menos el IMC medio poblacional para las hembras.
- Utilizando software estadístico, encontramos que el intervalo de confianza del 95% para μ 1 — μ 2 es aproximadamente (0.63, 2.64).
- Esto se encuentra en SPSS en la fila de varianzas desiguales asumidas bajo columnas de intervalo de confianza de 95% y en SAS en la ROW SATTERTHWAITE bajo columna de 95% CL MEAN.
- Interpretación:
- Con 95% de confianza que el IMC medio de la población para los machos es entre 0.63 y 2.64 unidades mayor que el de las hembras.
- O
- Con 95% de confianza que el IMC medio de la población para las hembras es entre 0.63 y 2.64 unidades menor que el de los machos.
- Por lo tanto, el intervalo de confianza cuantifica el efecto de la variable explicativa (género) sobre la respuesta (IMC). Observe que no podemos implicar un efecto causal del género sobre el IMC basado solo en este resultado ya que podría haber muchas variables al acecho, no contabilizadas en este análisis, que podrían ser parcial o incluso completamente responsables de esta diferencia.
- Nota: El intervalo de confianza no contiene cero (ambos valores son positivos en función de cómo elegimos nuestros grupos) y así usando el intervalo de confianza podemos rechazar la hipótesis nula aquí.
Importancia práctica:
- Definitivamente deberíamos preguntarnos si esto es prácticamente significativo
- ¿Es significativa aquí una verdadera diferencia en las medias poblacionales representadas por nuestra estimación a partir de estos datos? ¿Es una diferencia en el IMC de entre 0.53 y 2.64 de interés?
- Te dejaré considerar y responder por ti mismo.
Salida SPSS para este ejemplo (Salida no paramétrica para los Ejemplos 1 y 2)
Salida SAS y Código SAS (Incluye Prueba No Paramétrica)
Nota: En la salida SAS no está formateada la variable género, en este caso Hombres = 0 y Mujeres = 1.
Comentarios:
Podrías preguntarte: “¿Dónde usamos el estadístico de prueba?”
Es cierto que para todos los fines prácticos lo único que tenemos que hacer es verificar que se cumplan las condiciones que nos permiten utilizar la prueba t de dos muestras, levantar el valor p de la salida y sacar nuestras conclusiones en consecuencia.
Sin embargo, consideramos que es importante mencionar el estadístico de prueba por dos razones:
- El estadístico de prueba es lo que hay detrás de escena; en base a su distribución nula y su valor, se calcula el valor p.
- Además de ser la clave para calcular el valor p, el estadístico de prueba también es en sí mismo una medida de la evidencia almacenada en los datos contra Ho. Como mencionamos, mide (en errores estándar) cuán diferentes son nuestros datos de lo que se afirma en la hipótesis nula.
Ahora prueba algunas actividades más por ti mismo.
¿Conseguí esto? Prueba T de dos muestras e intervalo de confianza relacionado
(versión no interactiva — alerta de spoiler)
Alternativa no paramétrica: Prueba de suma de rangos de Wilcoxon (U de Mann-Whitney)
Objetivos de aprendizaje
LO 5.1: Para una situación de análisis de datos que involucre dos variables, determinar el método alternativo apropiado (no paramétrico) cuando no se cumplan los supuestos de nuestros métodos estándar.
Analizaremos una prueba no paramétrica en el entorno de dos muestras independientes. Más detalles se discutirán más adelante (Detalles para Alternativas No Paramétricas).
- La prueba de suma de rangos de Wilcoxon (prueba U de Mann-Whitney) es una prueba general para comparar dos distribuciones en muestras independientes. Es una alternativa de uso común a la prueba t de dos muestras cuando no se cumplen los supuestos.
k > 2 Muestras Independientes
CO-4: Distinguir entre diferentes escalas de medición, elegir los métodos estadísticos descriptivos e inferenciales adecuados con base en estas distinciones e interpretar los resultados.
Objetivos de aprendizaje
LO 4.35: Para una situación de análisis de datos que involucre dos variables, elija el método inferencial apropiado para examinar la relación entre las variables y justificar la elección.
Objetivos de aprendizaje
LO 4.36: Para una situación de análisis de datos que involucre dos variables, llevar a cabo el método inferencial apropiado para examinar las relaciones entre las variables y sacar las conclusiones correctas en contexto.
CO-5: Determinar alternativas metodológicas preferidas a los métodos estadísticos de uso común cuando no se cumplen los supuestos.
REVISIÓN: Unidad 1 Caso C-Q
Video
Video: 2 Muestras Independientes">K > 2 Muestras Independientes (21:15)
Tutoriales SAS relacionados
- 7A (2:32) Resúmenes numéricos por grupos
- 7B (3:03) Parcelas de caja lado a lado
- ANOVA de una vía 7D (4:07)
Tutoriales relacionados con SPSS
- 7A (3:29) Resúmenes numéricos por grupos
- 7B (1:59) Parcelas de caja lado a lado
- ANOVA de una vía 7D (4:22)
Introducción
En esta parte, seguimos manejando situaciones que involucran una variable explicativa categórica y una variable de respuesta cuantitativa, que es el caso C→Q.
Aquí un resumen de las pruebas que hemos cubierto para el caso donde k = 2. Los métodos en BOLD son nuestro foco principal en esta unidad.
Hasta el momento hemos discutido los diseños de dos muestras y pares emparejados, en los que la variable explicativa categórica es de dos valores. Como vimos, en estos casos, examinar la relación entre las variables explicativas y de respuesta equivale a comparar la media de la variable de respuesta (Y) en dos poblaciones, las cuales son definidas por los dos valores de la variable explicativa (X). La diferencia entre las dos muestras y los diseños de pares emparejados es que en la primera, las dos muestras son independientes, y en las segundas, las muestras son dependientes.
Muestras independientes (más énfasis) |
Muestras Dependientes (Menos Énfasis) |
Pruebas estándar
Prueba no paramétrica
|
Prueba estándar
Pruebas no paramétricas
|
Pasamos ahora al caso donde k > 2 cuando tenemos muestras independientes. Aquí un resumen de las pruebas que aprenderemos para el caso donde k > 2. Aviso no cubriremos el caso de muestras dependientes en este curso.
Muestras Independientes (Solo Énfasis) |
Muestras dependientes (no discutidas) |
Pruebas estándar
Prueba no paramétrica
|
Prueba estándar
|
Aquí, como en el caso de dos valores, hacer inferencias sobre la relación entre las variables explicativas (X) y la respuesta (Y) equivale a comparar las medias de la variable de respuesta en las poblaciones definidas por los valores de la variable explicativa, donde depende el número de medias que estamos comparando, de curso, sobre el número de valores de X.
A diferencia del caso de dos valores, donde observamos dos subcasos (1) cuando las muestras son independientes (diseño de dos muestras) y (2) cuando las muestras son dependientes (diseño de pares emparejados, aquí, solo vamos a discutir el caso donde las muestras son independientes. En otras palabras, sólo vamos a extender el diseño de dos muestras a más de dos muestras independientes.
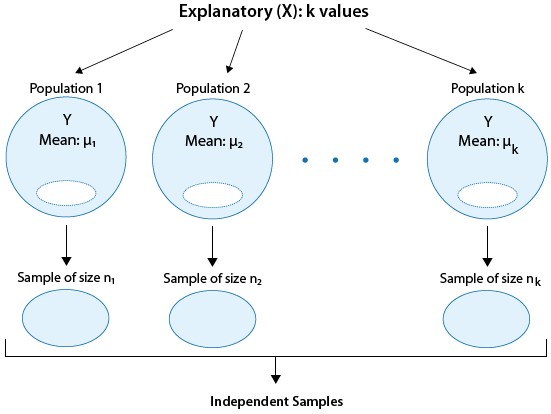
El método inferencial para comparar más de dos medias que vamos a introducir en esta parte se llama Analysis Of Variance (abreviado como ANOVA), y la prueba asociada a este método se llama la prueba F de ANOVA.
En la mayoría de los programas informáticos, los datos deben organizarse de manera que cada fila contenga una observación con una variable registrando X y otra variable registrando Y para cada observación.
Comparación de dos o más medias: la prueba F de ANOVA
Objetivos de aprendizaje
LO 4.38: En un contexto dado, determinar el método estándar apropiado para comparar grupos y proporcionar las conclusiones correctas dado el resultado del software apropiado.
Objetivos de aprendizaje
LO 4.39: En un contexto dado, establecer las hipótesis nulas y alternativas apropiadas para comparar grupos.
Como mencionamos anteriormente, la prueba que presentaremos se llama la prueba F de ANOVA, y como verás, esta prueba es diferente en dos formas de todas las pruebas que hemos presentado hasta el momento:
- A diferencia de las pruebas anteriores, donde teníamos tres posibles hipótesis alternativas para elegir (dependiendo del contexto del problema), en la prueba F de ANOVA solo hay una alternativa, lo que en realidad simplifica la vida.
- El estadístico de prueba no tendrá la misma estructura que los estadísticos de prueba que hemos visto hasta ahora. En otras palabras, no tendrá la forma:
\(\text{test statistic} = \dfrac{\text{estimator - null value}}{\text{standard error of estimator}}\)
sino una estructura diferente que captura la esencia de la prueba F, y aclara de dónde viene el nombre “análisis de varianza”.
¿Cuál es la idea detrás de comparar más de dos medios?
La pregunta que debemos responder es: ¿Las diferencias entre las medias de la muestra se deben a diferencias verdaderas entre los μ (hipótesis alternativa), o simplemente por variabilidad de muestreo o probabilidad aleatoria (hipótesis nula)?
Aquí hay dos conjuntos de diagramas de caja que representan dos escenarios posibles:
Escenario #1
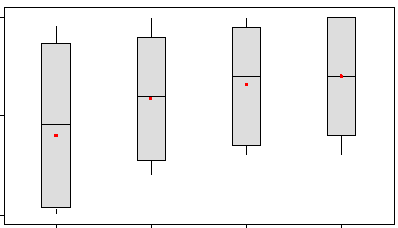
- Debido a la gran cantidad de propagación dentro de los grupos, estos datos muestran parcelas de caja con mucha superposición.
- Se podrían imaginar los datos derivados de 4 muestras aleatorias tomadas de 4 poblaciones, todas teniendo la misma media de alrededor de 11 o 12.
- El primer grupo de valores puede haber estado un poco en el lado bajo, y los otros tres un poco en el lado alto, pero es concebible que tales diferencias se hayan producido por casualidad.
- Este sería el caso si la hipótesis nula, alegando medias iguales de población, fuera cierta.
Escenario #2
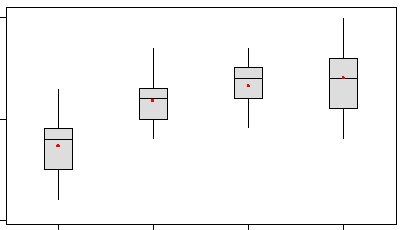
- Debido a la pequeña cantidad de propagación dentro de los grupos, estos datos muestran parcelas de caja con muy poca superposición.
- Sería muy difícil creer que estemos muestreando de cuatro grupos que tienen iguales medias poblacionales.
- Este sería el caso si la hipótesis nula, alegando medias iguales de población, fuera falsa.
Así, en el lenguaje de las pruebas de hipótesis, diríamos que si los datos se configuraran como están en el escenario 1, no rechazaríamos la hipótesis nula de que las medias poblacionales eran iguales para los k grupos.
Si los datos se configuraran tal como están en el escenario 2, rechazaríamos la hipótesis nula, y concluiríamos que no todas las medias poblacionales son iguales para los k grupos.
Resumamos lo que aprendimos de esto.
- La pregunta que debemos responder es: ¿Las diferencias entre las medias de la muestra se deben a diferencias verdaderas entre los μ (hipótesis alternativa), o simplemente por variabilidad del muestreo (hipótesis nula)?
Para poder responder a esta pregunta usando datos, necesitamos observar la variación entre las medias de la muestra, pero esto por sí solo no es suficiente.
Es necesario observar la variación entre las medias de la muestra en relación con la variación dentro de los grupos. En otras palabras, tenemos que mirar la cantidad:

que mide hasta qué punto la diferencia entre las medias muestrales para nuestros grupos domina sobre la variación habitual dentro de los grupos muestreados (lo que refleja diferencias en individuos que son típicas en muestras aleatorias).
Cuando la variación dentro de los grupos es grande (como en el escenario 1), la variación (diferencias) entre las medias de la muestra puede llegar a ser insignificante dando como resultado datos que proporcionan muy poca evidencia contra Ho. Cuando la variación dentro de los grupos es pequeña (como en el escenario 2), la variación entre las medias muestrales domina sobre ella, y los datos tienen evidencia más fuerte contra Ho.
Tiene una estructura diferente a todas las estadísticas de prueba que hemos visto hasta ahora, pero es similar en que sigue siendo una medida de la evidencia contra H 0. Cuanto mayor es F (lo que ocurre cuando el denominador, la variación dentro de los grupos, es pequeña en relación con el numerador, la variación entre las medias de la muestra), más evidencia tenemos contra H 0.
Mirar esta relación de variaciones es la idea detrás de la comparación de más de dos medias; de ahí el nombre de análisis de varianza (ANOVA).
Ahora pon a prueba tu comprensión de esta idea.
Aprende haciendo: Idea de ANOVA unidireccional
(Versión no interactiva — Alerta de spoiler)
Comentarios
- El enfoque aquí es que entiendas la idea detrás de esta estadística de prueba, por lo que no entramos en detalles sobre cómo se miden las dos variaciones. En cambio, confiamos en la salida de software para obtener la estadística F.
- Esta prueba se llama la prueba F de ANOVA.
- Hasta el momento, hemos explicado la parte ANOVA del nombre.
- Con base en las pruebas anteriores que introdujimos, no debería sorprender que la parte “prueba F” provenga del hecho de que la distribución nula del estadístico de prueba, bajo la cual se calculan los valores p, se denomina distribución F.
- Diremos muy poco sobre la distribución F en este curso, que esencialmente se limitará a este comentario y al siguiente.
- Es bastante sencillo decidir si una estadística z es grande. Incluso sin tablas, ya deberíamos darnos cuenta de que una estadística z de 0.8 no es especialmente grande, mientras que una estadística z de 2.5 es grande.
- En el caso del estadístico t, es menos sencillo, ya que existe una distribución t diferente para cada tamaño de muestra n (y grados de libertad n − 1).
- Sin embargo, el hecho de que una distribución t con un gran número de grados de libertad esté muy cerca de la distribución z (normal estándar) puede ayudar a evaluar la magnitud del estadístico de la prueba t.
- Cuando se debe evaluar el tamaño del estadístico F, la tarea es aún más complicada, ya que hay una distribución F diferente para cada combinación del número de grupos que estamos comparando y el tamaño total de la muestra.
- Sin embargo, diremos que para la mayoría de las situaciones, una estadística F mayor a 4 se consideraría bastante grande, pero se necesitan tablas o software para obtener una evaluación verdaderamente precisa.
Pasos para ANOVA unidireccional
Aquí hay una declaración completa del proceso para la prueba F de ANOVA:
Paso 1: Exponer las hipótesis
La hipótesis nula afirma que no existe relación entre X e Y. Dado que la relación se examina comparando las medias de Y en las poblaciones definidas por los valores de X (μ 1, μ 2,..., μ k), ninguna relación significaría que todas las medias son iguales.
Por lo tanto, la hipótesis nula de la prueba F es:
- Ho: μ 1 = μ 2 =... = μ k. (No hay relación entre X e Y.)
Como mencionamos anteriormente, aquí tenemos solo una hipótesis alternativa, que afirma que existe una relación entre X e Y. En términos de los medios μ 1, μ 2,..., μ k, simplemente dice lo contrario de la hipótesis nula, que no todos los medios son iguales, y simplemente escribimos:
- Ha: no todos los μ son iguales. (Existe una relación entre X e Y.)
Aprende haciendo: ANOVA unidireccional — PASO 1
(Versión no interactiva — Alerta de spoiler)
Comentarios:
- La alternativa de la prueba F de ANOVA simplemente establece que no todas las medias son iguales, y no es específica sobre la manera en que son diferentes.
- Otra forma de formular la alternativa es
- Ha: al menos dos μ son diferentes
- Advertencia: Es incorrecto decir que la alternativa es μ 1 ≠ μ 2 ≠... ≠ μ k. Esta afirmación es MUCHO más fuerte que nuestra hipótesis alternativa y dice que TODOS los medios son diferentes de TODOS los demás medios
- Tenga en cuenta que hay muchas formas para que μ1, μ2, μ3, μ4 no sean todos iguales, y μ1 ≠ μ2 ≠ μ3 ≠ μ4 es solo una de ellas. Otra forma podría ser μ1 = μ2 = μ3 ≠ μ4 o μ1 = μ2 ≠ μ3 = μ4. La alternativa de la prueba F de ANOVA simplemente establece que no todas las medias son iguales, y no es específica sobre la manera en que son diferentes.
Paso 2: Obtener datos, verificar condiciones y resumir datos
La prueba F de ANOVA se puede utilizar de forma segura siempre que se cumplan las siguientes condiciones:
- Las muestras extraídas de cada una de las poblaciones que comparamos son independientes.
- Nos encontramos en uno de los dos escenarios siguientes:
(i) Cada una de las poblaciones es normal, o más específicamente, la distribución de la respuesta Y en cada población es normal, y las muestras son aleatorias (o al menos pueden considerarse como tales). En la práctica, verificar la normalidad en las poblaciones se realiza observando cada una de las muestras mediante un histograma y comprobando si hay algún signo de que las poblaciones no son normales. Tales signos podrían ser asimetría extrema y/o valores atípicos extremos.
(ii) Se sabe o se descubre que las poblaciones no son normales, pero el tamaño muestral de cada una de las muestras aleatorias es suficientemente grande (podemos usar la regla general de que un tamaño de muestra mayor a 30 se considera suficientemente grande).
- Todas las poblaciones tienen la misma desviación estándar.
Puede verificar esta condición usando la regla general de que la relación entre la desviación estándar de la muestra más grande y la más pequeña es menor que 2. Si ese es el caso, esta condición se considera satisfecha.
Se puede verificar esta condición usando una prueba formal similar a la utilizada en la prueba t de dos muestras aunque no cubriremos ninguna prueba formal.
Aprende haciendo: ANOVA unidireccional — PASO 2
(Versión no interactiva — Alerta de spoiler)
Estadística de prueba
- Si nuestras condiciones están satisfechas contamos con el estadístico de prueba.

- El estadístico sigue una distribución F con k-1 grados de libertad del numerador y n-k grados de libertad denominador.
- Donde n es el tamaño total (combinado) de la muestra y k es el número de grupos que se comparan.
- Confiaremos en el software para calcular el estadístico de prueba y el valor p para nosotros.
Paso 3: Encuentre el valor p de la prueba usando el estadístico de prueba de la siguiente manera
- El valor p de la prueba F de ANOVA es la probabilidad de obtener un estadístico F tan grande como se obtuvo (o incluso mayor), si Ho hubiera sido verdadero (todas las k medias de la población son iguales).
- Es decir, nos dice lo sorprendente que es encontrar datos como los observados, asumiendo que no hay diferencia entre la población significa μ 1, μ 2,..., μ k.
Paso 4: Conclusión
Como es habitual, basamos nuestra conclusión en el valor p.
- Un pequeño valor p nos dice que nuestros datos contienen mucha evidencia contra Ho. Más específicamente, un pequeño valor p nos dice que las diferencias entre las medias de la muestra son estadísticamente significativas (es poco probable que haya ocurrido por casualidad), y por lo tanto rechazamos Ho.
- Conclusión: Existe suficiente evidencia de que la variable explicativa categórica está relacionada con (o asociada con) la variable de respuesta cuantitativa. Más específicamente, hay suficiente evidencia de que existen diferencias entre al menos dos de las medias poblacionales (hay algunas diferencias en las medias poblacionales).
- Si el valor p no es pequeño, no tenemos evidencia estadística suficiente para rechazar a Ho.
- Conclusión: NO hay evidencia suficiente de que la variable explicativa categórica esté relacionada con (o asociada con) la variable de respuesta cuantitativa. Más específicamente, NO hay evidencia suficiente de que existan diferencias entre al menos dos de las medias poblacionales.
- Un nivel de significancia (probabilidad de corte) de 0.05 puede ayudar a determinar lo que se considera un valor p pequeño.
Comentario Final
Tenga en cuenta que cuando rechazamos Ho en la prueba F de ANOVA, todo lo que podemos concluir es que
- no todos los medios son iguales, o
- hay algunas diferencias entre las medias, o
- la respuesta Y está relacionada con el explicativo X.
Sin embargo, la prueba F de ANOVA no proporciona ninguna idea inmediata de por qué se rechazó Ho, o en otras palabras, no nos dice de qué manera las medias poblacionales de los grupos son diferentes. Como ayuda exploratoria (o visual) para obtener esa visión, podemos echar un vistazo a los intervalos de confianza para las medias de población grupal. Más específicamente, podemos ver cuál de los intervalos de confianza se superponen y cuáles no.
Comparaciones múltiples:
- Cuando comparamos los intervalos de confianza estándar del 95% de esta manera, tenemos una mayor probabilidad de cometer un error de tipo I ya que cada intervalo tiene un error del 5% individualmente.
- Existen muchos procedimientos de comparación múltiple, todos los cuales proponen métodos alternativos para determinar qué pares de medias son diferentes.
- Vamos a ver algunos de estos en el software solo para mostrarte un poco sobre este tema pero no lo cubriremos oficialmente en este curso.
- El objetivo es proporcionar una tasa de error general tipo I no mayor al 5% para todas las comparaciones realizadas.
Ahora veamos algunos ejemplos usando datos reales.
EJEMPLO: ¿La “frustración académica” está relacionada con la especialización?
Un decano universitario cree que los estudiantes con diferentes especializaciones pueden experimentar diferentes niveles de frustración académica. Se pide a muestras aleatorias de talla 35 de las carreras de Negocios, Inglés, Matemáticas y Psicología que califiquen su nivel de frustración académica en una escala de 1 (más baja) a 20 (más alta).
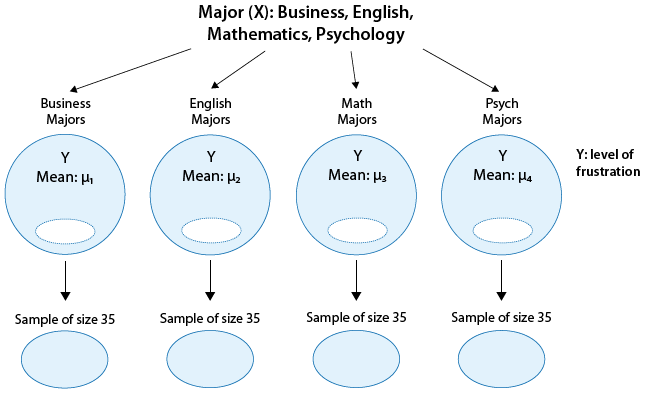
La cifra resalta lo que ya hemos mencionado: examinar la relación entre mayor (X) y nivel de frustración (Y) equivale a comparar los niveles medios de frustración entre las cuatro mayores definidas por X. Además, la cifra nos recuerda que estamos ante un caso donde las muestras son independientes.
Paso 1: Exponer las hipótesis
Las hipótesis correctas son:
- Ho: μ 1 = μ 2 = μ 3 = μ 4.
(NO hay relación entre el nivel de frustración mayor y académico). - Ha: no todos los μ son iguales.
(Existe una relación entre el nivel de frustración mayor y académico).
Paso 2: Obtener datos, verificar condiciones y resumir datos
Datos: formato SPSS, formato SAS, formato Excel, formato CSV
En nuestro ejemplo se cumplen todas las condiciones:
- Todas las muestras fueron elegidas al azar, por lo que son independientes.
- Los tamaños de muestra son lo suficientemente grandes (n = 35) como para que realmente no tengamos que preocuparnos por la normalidad; sin embargo, veamos los datos usando diagramas de caja lado a lado, solo para tener una idea de ello:

- Los datos sugieren que el nivel de frustración de los estudiantes de negocios es generalmente inferior al de los estudiantes de las otras tres carreras. La prueba F de ANOVA nos dirá si estas diferencias son significativas.
La regla general se cumple desde 3.082/2.088 < 2. Vamos a ver la prueba formal en el software.
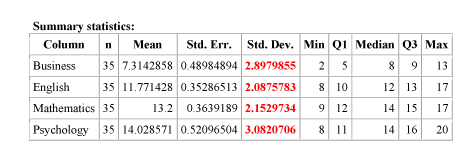
Estadística de prueba: (salida de Minitab)
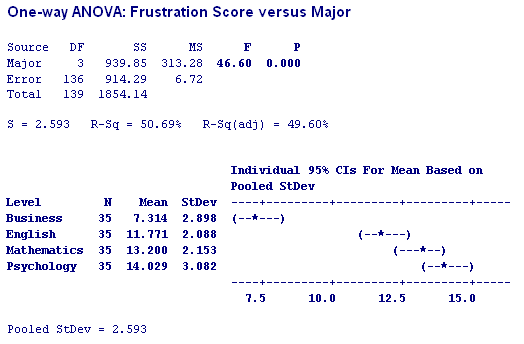
- Se han resaltado las partes de la salida en las que nos centraremos aquí. En particular, señalar que el estadístico F es 46.60, que es muy grande, lo que indica que los datos proporcionan mucha evidencia contra Ho (también podemos ver que el valor p es tan pequeño que se reporta que es 0, lo que respalda esa conclusión también).
Paso 3: Encuentre el valor p de la prueba usando el estadístico de prueba de la siguiente manera
- Como ya notamos antes, el valor p en nuestro ejemplo es tan pequeño que se reporta que es 0.000, diciéndonos que sería casi imposible obtener datos como los observados si el nivel medio de frustración de las cuatro mayores hubiera sido el mismo (como afirma la hipótesis nula).
Paso 4: Conclusión
- En nuestro ejemplo, el valor p es extremadamente pequeño —cercano a 0—, lo que indica que nuestros datos proporcionan evidencia extremadamente sólida para rechazar a Ho.
- Conclusión: Existe suficiente evidencia de que el nivel medio de frustración de la población de las cuatro carreras no es el mismo, o en otras palabras, que las mayores sí tienen un efecto en los niveles de frustración académica de los estudiantes en la escuela donde se realizó la prueba.
Como seguimiento, podemos construir intervalos de confianza (o realizar múltiples comparaciones como lo haremos en el software). Esto nos permite entender mejor qué medios poblacionales son susceptibles de ser diferentes.
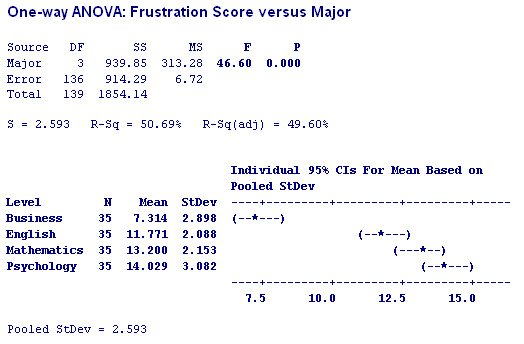
En este caso, las carreras empresariales son claramente inferiores en la escala de frustración que otras especializaciones. También es posible que las carreras de inglés sean menores que las de psicología basadas en los intervalos de confianza individuales del 95% en cada grupo.
Salida SAS y código SAS (incluye prueba no paramétrica)
Aquí hay otro ejemplo
EJEMPLO: Nivel de Lectura en Publicidad
¿Los anunciantes alteran el nivel de lectura de sus anuncios en función del público objetivo de la revista en la que se anuncian?
En 1981 se realizó un estudio de anuncios de revistas (F.K. Shuptrine y D.D. McVicker, “Readability Levels of Magazine Ads”, Journal of Advertising Research, 21:5, octubre de 1981). Los investigadores seleccionaron muestras aleatorias de anuncios de cada uno de tres grupos de revistas:
- Grupo 1: revistas de nivel educativo más alto (como Scientific American, Fortune, The New Yorker)
- Grupo 2—revistas de nivel educativo medio (como Sports Illustrated, Newsweek, People)
- Grupo 3: revistas de nivel educativo más bajo (como National Enquirer, Grit, True Confessions)
La medida que los investigadores utilizaron para evaluar el nivel de los anuncios fue el número de palabras en el anuncio. Se seleccionaron 18 anuncios al azar de cada uno de los grupos de revistas, y se registró el número de palabras por anuncio.
La siguiente figura resume este problema:
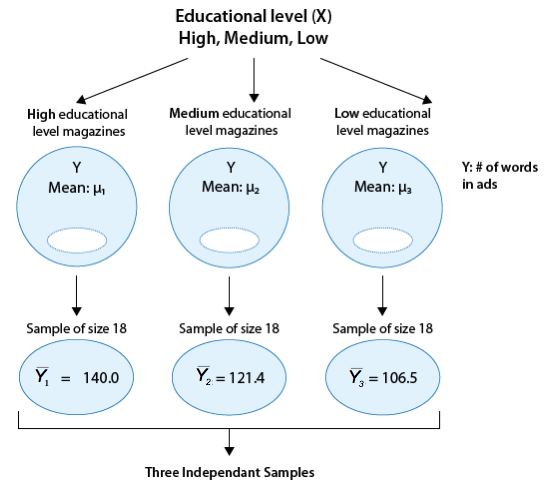
Nuestra pregunta de interés es si el número de palabras en los anuncios (Y) está relacionado con el nivel educativo de la revista (X). Para responder a esta pregunta, necesitamos comparar μ 1, μ 2 y μ 3, el número medio de palabras en los anuncios de los tres grupos de revistas. Obsérvese en la figura que se proporcionan los medios de muestra. Parece que lo que sugieren los datos tiene sentido; las revistas del grupo 1 tienen el mayor número de palabras por anuncio (en promedio) seguidas por el grupo 2, y luego el grupo 3.
La pregunta es si estas diferencias entre las medias de la muestra son significativas. En otras palabras, ¿las diferencias entre las medias de muestra observadas son debidas a verdaderas diferencias entre los μ o simplemente por variabilidad muestral? Para responder a esta pregunta, necesitamos llevar a cabo la prueba F de ANOVA.
Paso 1: Afirmando las hipótesis.
Estamos probando:
- Ho: μ 1 = μ 2 = μ 3.
(NO hay relación entre el nivel educativo y el número de palabras en los anuncios.) - Ha: no todos los μ son iguales.
(Existe una relación entre el nivel educativo y el número de palabras en los anuncios.)
Conceptualmente, la hipótesis nula afirma que el número de palabras en los anuncios no está relacionado con el nivel educativo de la revista, y la hipótesis alternativa afirma que existe una relación.
Paso 2: Comprobando las condiciones y resumiendo los datos.
- (i) Los anuncios fueron seleccionados al azar de cada grupo de revistas, por lo que las tres muestras son independientes.
Para verificar las dos siguientes condiciones, tendremos que mirar los datos (condición ii) y calcular las desviaciones estándar de la muestra de las tres muestras (condición iii).
- Aquí están los diagramas de caja lado a lado de los datos:
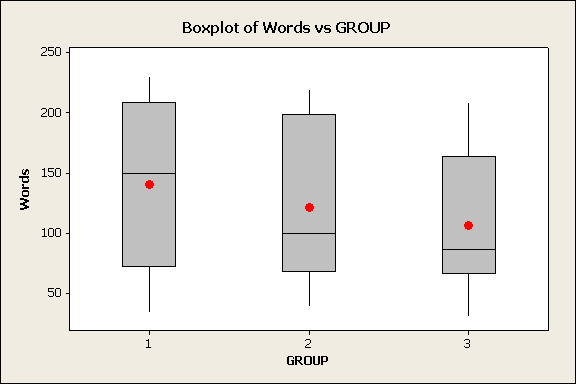
- Y las desviaciones estándar:
- Grupo 1 StDev: 74.0
- Grupo 2 StDev: 64.3
- Grupo 3 StDev: 57.6
Usando lo anterior, podemos abordar las condiciones (ii) y (iii)
- (ii) La gráfica no muestra ninguna violación alarmante del supuesto de normalidad. Parece que hay cierta asimetría en los grupos 2 y 3, pero no extremadamente así, y no hay valores atípicos en los datos.
- (iii) Podemos suponer que se cumple el supuesto de desviación estándar igual ya que se cumple la regla general: la desviación estándar muestral más grande de las tres es 74 (grupo 1), la más pequeña es 57.6 (grupo 3) y 74/57.6 < 2.
Antes de seguir adelante, volvamos a ver la gráfica. Es fácil ver la tendencia de las medias muestrales (indicadas por círculos rojos).
Sin embargo, hay tanta variación dentro de cada uno de los grupos que hay casi una superposición completa entre las tres parcelas de caja, y las diferencias entre las medias se ven eclipsadas y parecen algo que podría haber sucedido solo por casualidad.
Sigamos adelante y veamos si la prueba F de ANOVA apoyará esta observación.
- Test Statistic: Usando software estadístico para realizar la prueba F de ANOVA, encontramos que el estadístico F es 1.18, que no es muy grande. También encontramos que el valor p es 0.317.
Paso 3. Encontrar el valor p.
- El valor p es de 0.317, lo que nos dice que obtener datos como los observados no es muy sorprendente asumiendo que no hay diferencias entre los tres grupos de revistas con respecto al número medio de palabras en los anuncios (que es lo que H o afirma).
- En otras palabras, el gran valor p nos dice que es bastante razonable que las diferencias entre las medias de muestra observadas pudieran haber ocurrido solo por casualidad (es decir, debido a la variabilidad del muestreo) y no por verdaderas diferencias entre las medias.
Paso 4: Hacer conclusiones en contexto.
- El gran valor p indica que los resultados no son estadísticamente significativos, y que no podemos rechazar H o.
- Conclusión: El estudio no aporta evidencia de que el número medio de palabras en los anuncios esté relacionado con el nivel educativo de la revista. Es decir, el estudio no aporta evidencia de que los anunciantes alteren el nivel de lectura de sus anuncios (medido por el número de palabras) con base en el nivel educativo del público objetivo de la revista.
Ahora prueba uno por ti mismo.
Aprende haciendo: ANOVA unidireccional — Frecuencia de parpadeo
(Versión no interactiva — Alerta de spoiler)
Intervalos de confianza
La prueba F de ANOVA no proporciona ninguna idea de por qué se rechazó H 0; no nos dice de qué manera μ1, μ2, μ3..., μk no son todos iguales. Nos gustaría saber qué pares de's no son iguales. Como ayuda exploratoria (o visual) para obtener esa visión, podemos echar un vistazo a los intervalos de confianza para los medios de población de grupoμ1, μ2, μ3..., μk que aparecen en la salida. Más específicamente, debemos mirar la posición de los intervalos de confianza y superponer/no solapar entre ellos.
* Si el intervalo de confianza para, digamos, μi se superpone con el intervalo de confianza para μj, entonces μi y μj comparten algunos valores plausibles, lo que significa que en base a los datos no tenemos evidencia de que estos dos sean diferentes.
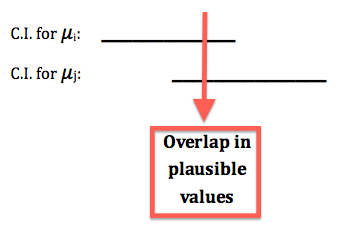
* Si el intervalo de confianza para μi no se solapa con el intervalo de confianza para μj, entonces μi y μj no comparten valores plausibles, lo que significa que los datos sugieren que estos dos son diferentes.
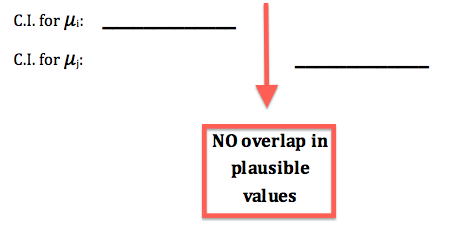
Además, si como en la figura por encima del intervalo de confianza (conjunto de valores plausibles) para μi se encuentra completamente por debajo del intervalo de confianza (conjunto de valores plausibles) para μj, entonces los datos sugieren que μi es menor que μj.
Ejemplo
Consideremos nuestro primer ejemplo sobre el nivel de frustración académica.
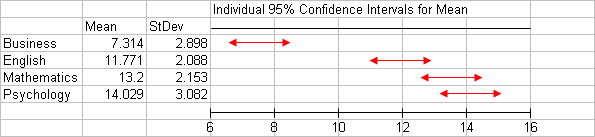
Con base en el pequeño valor p, rechazamos H o y concluimos que no las cuatro medias de nivel de frustración son iguales, o en otras palabras, que el nivel de frustración está relacionado con la especialización del estudiante. Para obtener más información sobre esa relación, podemos observar los intervalos de confianza anteriores (marcados en rojo). El intervalo de confianza superior es el conjunto de valores plausibles para μ 1, el nivel medio de frustración de los estudiantes de negocios. El intervalo de confianza por debajo de él es el conjunto de valores plausibles para μ 2, el nivel medio de frustración de los estudiantes de inglés, etc.
Lo que vemos es que el intervalo de confianza empresarial está muy por debajo de los otros tres (no se superpone con ninguno de ellos). El intervalo de confianza matemática se superpone tanto con los intervalos de confianza en inglés como con los de psicología; sin embargo, no hay superposición entre los intervalos de confianza en inglés y psicología.
Esto nos da la impresión de que el nivel medio de frustración de los estudiantes de negocios es menor que la media en las otras tres carreras. Dentro de las otras tres carreras, tenemos la impresión de que la frustración media de los estudiantes de matemáticas puede no diferir mucho de la media de los estudiantes de inglés y psicología, sin embargo la frustración media de los estudiantes de inglés puede ser menor que la media de los estudiantes de psicología.
Tenga en cuenta que esta es solo una forma exploratoria/visual de tener una impresión de por qué H o fue rechazado, no formal. Hay una forma formal de hacerlo que se llama “comparaciones múltiples”, que está más allá del alcance de este curso. Una extensión de este curso incluirá este tema en el futuro.
Alternativa no paramétrica: Prueba de Kruskal-Wallis
Objetivos de aprendizaje
LO 5.1: Para una situación de análisis de datos que involucre dos variables, determinar el método alternativo apropiado (no paramétrico) cuando no se cumplan los supuestos de nuestros métodos estándar.
Analizaremos una prueba no paramétrica en el ajuste de k > 2 muestras independientes. Cubriremos más detalles más adelante (Detalles para Alternativas No Paramétricas).
La prueba de Kruskal-Wallis es una prueba general para comparar distribuciones múltiples en muestras independientes y es una alternativa común al ANOVA unidireccional.
Detalles de Alternativas No Paramétricas en el Caso C-Q
Aprende haciendo: Ejemplos y ejercicios suplementarios para la Unidad 4B
(Versión no interactiva)
Precaución
Como mencionamos al final de la Introducción a la Unidad 4B, solo nos centraremos en las pruebas bilaterales para lo que resta de este curso. Las pruebas unilaterales son a menudo posibles, pero rara vez se utilizan en la investigación clínica.
CO-5: Determinar alternativas metodológicas preferidas a los métodos estadísticos de uso común cuando no se cumplen los supuestos.
Video
Video: Detalles de Alternativas No Paramétricas (17:38)
Tutoriales SAS relacionados
- 7E — (4:34) Pruebas no paramétricas para muestras independientes (k= 2 y k > 2)
- 8C — (5:20) Prueba T pareada y pruebas no paramétricas para muestras dependientes
Tutoriales relacionados con SPSS
- 7E — (3:57) Pruebas no paramétricas para muestras independientes (k= 2 y k > 2)
- 8D — (3:32) No paramétrico (emparejado) para muestras dependientes
Se mencionaron algunas alternativas no paramétricas a la prueba t pareada, la prueba t de dos muestras para muestras independientes y el ANOVA unidireccional.
Aquí proporcionamos más detalles y recursos para estas pruebas para aquellos de ustedes que deseen realizarlos en la práctica.
Pruebas no paramétricas
Las pruebas estadísticas que hemos discutido previamente requieren suposiciones sobre la distribución en la población o sobre los requisitos para utilizar una cierta aproximación como distribución muestral. Estos métodos se denominan paramétricos.
Cuando estos supuestos no son válidos, a menudo existen métodos alternativos para probar hipótesis similares. Las pruebas que requieren solo suposiciones distribucionales mínimas, si las hay, se denominan pruebas no paramétricas o libres de distribución.
En algunos casos, estas pruebas pueden llamarse pruebas exactas debido a que sus métodos de cálculo de valores p o intervalos de confianza no requieren aproximación matemática (fundamento de muchos métodos estadísticos).
Sin embargo, tenga en cuenta que cuando los supuestos se satisfacen con precisión, algunas pruebas “paramétricas” también pueden considerarse “exactas”.
Caso CQ — Pares emparejados
Analizaremos dos pruebas no paramétricas en el entorno de la muestra pareada.
La Prueba de Signo
La prueba de signos es una prueba muy general utilizada para comparar muestras pareadas. Se puede utilizar en lugar de la prueba T pareada si no se cumplen los supuestos aunque la siguiente prueba que discutamos es probablemente una mejor opción en ese caso como veremos. Sin embargo, la prueba de signos sí tiene algunas ventajas y vale la pena entenderla.
- La idea detrás de la prueba es encontrar el signo de las diferencias (positivas o negativas) y utilizar esta información para determinar si las medianas entre los dos grupos son las mismas.
- Si las dos mediciones pareadas provinieran de poblaciones con medianas iguales, esperaríamos que la mitad de las diferencias fueran positivas y la mitad negativas. Así, la distribución muestral de nuestro estadístico es simplemente un binomio con p = 0.5.
Esquema de Procedimiento para la PRUEBA DE SEÑAL
- Paso 1: Exponer las hipótesis
Las hipótesis son:
Ho: las medianas son iguales
Ja: las medianas no son iguales (son posibles pruebas unilaterales)
- Paso 2: Obtener datos, verificar condiciones y resumir datos
Requerimos una muestra aleatoria (o al menos puede considerarse aleatoria en contexto).
La prueba de signos se puede utilizar para cualquier dato para el que se pueda obtener el signo de la diferencia. Por lo tanto, se puede utilizar para:
medidas cuantitativas (continuas o discretas)
Ejemplos: Presión arterial sistólica, número de bebidas
medidas ordinales (categóricas)
Ejemplos: Escalas de calificación, Grados de letras
medidas binarias (categóricas) donde solo podemos decir si un par es “más grande” o “más pequeño” en comparación con el otro par
Ejemplos: ¿El brazo izquierdo está más o menos quemado por el sol que el brazo derecho? , ¿Hubo mejoría en el dolor después del tratamiento?
Por esta razón, ¡esta prueba es muy aplicable!
Los datos se resumen mediante un estadístico de prueba que cuenta el número de diferencias positivas (o negativas). Se descartan todos los lazos (cero diferencias).
- Paso 3: Encuentre el valor p de la prueba usando el estadístico de prueba de la siguiente manera
Los valores p se calculan utilizando la distribución binomial (o una aproximación normal para muestras grandes). Confiaremos en el software para obtener el valor p para esta prueba.
- Paso 4: Conclusión
La decisión se toma de la misma manera que otras pruebas.
Podemos expresar nuestra conclusión en términos de las medianas en las dos poblaciones o en términos de la relación entre la variable explicativa categórica (X) y la variable respuesta (Y).
OPCIONAL: Para más detalles visite The Sign Test en el contenido en línea de Penn State para STAT 415.
La prueba de rango de Wilcoxon:
La prueba de rango firmado de Wilcoxon es una prueba general para comparar distribuciones en muestras pareadas. Esta prueba suele ser la alternativa preferida a la prueba t pareada cuando no se cumplen los supuestos.
La idea detrás de la prueba es determinar si las dos poblaciones parecen ser iguales o diferentes con base en los rangos de las diferencias absolutas (en lugar de la magnitud de las diferencias). Los procedimientos de clasificación se utilizan comúnmente en métodos no paramétricos, ya que esto modera el efecto de cualquier valor atípico.
Tenemos una suposición para esta prueba. Suponemos que la distribución de las diferencias es simétrica.
Bajo este supuesto, si las dos mediciones pareadas provinieran de las poblaciones con medios/medianas iguales, esperaríamos que los dos conjuntos de rangos (los de diferencias positivas y los de diferencias negativas) se distribuyeran de manera similar. Si aquí hay una gran diferencia, esto da evidencia de una verdadera diferencia.
Esquema del Procedimiento para la Prueba de Rango Firmado de Wilcoxon
- Paso 1: Exponer las hipótesis
Las hipótesis son:
Ho: los medios/medianas son iguales
Ha: los medios/medianas no son iguales (son posibles pruebas unilaterales)
- Paso 2: Obtener datos, verificar condiciones y resumir datos
Tenemos una muestra aleatoria y asumimos que la distribución de las diferencias es simétrica por lo que debemos verificar para asegurarnos de que no hay una asimetría clara a la distribución de las diferencias.
La prueba de rango firmado de Wilcoxon se puede utilizar para datos cuantitativos u ordinales (pero no binarios como para la prueba de signos).
Los datos se resumen mediante un estadístico de prueba que cuenta la suma de los rangos positivos (o negativos). Cualquier diferencia cero se descarta.
Para clasificar los pares, encontramos las diferencias (tanto como lo hicimos en la prueba t pareada), tomamos el valor absoluto de estas diferencias y clasificamos los pares desde 1 = diferencia distinta de cero más pequeña hasta m = mayor diferencia distinta de cero, donde m = número de pares distintos de cero.
Luego determinamos qué rangos vinieron de diferencias positivas (o negativas) y encontramos la suma de estos rangos.
No estarás realizando esta prueba a mano. Simplemente queremos explicar algo de la lógica detrás de escena para estas pruebas.
- Paso 3: Encuentre el valor p de la prueba usando el estadístico de prueba de la siguiente manera
Los valores p se calculan utilizando una distribución específica para esta prueba. Confiaremos en el software para obtener el valor p para esta prueba.
- Paso 4: Conclusión
La decisión se toma de la misma manera que otras pruebas. Podemos expresar nuestra conclusión en términos de las medias o medianas en las dos poblaciones o en términos de la existencia o inexistencia de una relación entre la variable explicativa categórica (X) y la variable respuesta (Y).
OPCIONAL: Para más detalles sobre estas pruebas visita The Wilcoxon Signed Rank Test en el contenido en línea de Penn State para STAT 415.
Comentarios:
- La prueba de signos tiende a tener una potencia mucho menor que la prueba t pareada o la prueba de rango firmado de Wilcoxon. Es decir, la prueba de signos tiene menos posibilidades de poder detectar una verdadera diferencia que las otras pruebas. Es, sin embargo, aplicable en el caso en que solo sepamos “mejor” o “peor” para cada par, donde los otros dos métodos no lo son.
- La prueba de rango con firma de Wilcoxon es comparable a la prueba t pareada en potencia e incluso puede funcionar mejor que la prueba t pareada bajo ciertas condiciones. En particular, esto puede ocurrir cuando hay algunos valores atípicos muy grandes, ya que estos valores atípicos pueden afectar en gran medida nuestra estimación del error estándar en la prueba t pareada, ya que se basa en la desviación estándar de la muestra que es altamente afectada por dichos valores atípicos.
- Tanto la prueba de signos como la prueba de rango firmado de Wilcoxon también se pueden usar para una muestra. En ese caso, debe especificar el valor nulo y calcular las diferencias entre el valor observado y el valor nulo (en lugar de la diferencia entre dos pares).
Caso CQ — Dos Muestras Independientes — Prueba de Suma de Rango de Wilcoxon (U de Mann-Whitney):
Analizaremos una prueba no paramétrica en el entorno de dos muestras independientes.
La prueba de suma de rangos de Wilcoxon (prueba U de Mann-Whitney) es una prueba general para comparar dos distribuciones en muestras independientes. Es una alternativa de uso común a la prueba t de dos muestras cuando no se cumplen los supuestos.
La idea detrás de la prueba es determinar si las dos poblaciones parecen ser iguales o diferentes en función de las filas de los valores en lugar de la magnitud. Los procedimientos de clasificación se utilizan comúnmente en métodos no paramétricos, ya que esto modera el efecto de cualquier valor atípico.
Hay muchas maneras de formular esta prueba. Para nuestros fines, asumiremos que la variable cuantitativa (Y) es una variable aleatoria continua (o puede tratarse como continua, como para recuentos muy grandes) y que nos interesa probar si hay un “cambio” en la distribución. Es decir, suponemos que la distribución es la misma excepto que en un grupo la distribución es mayor (o menor) que en el otro.
- Paso 1: Exponer las hipótesis
Suponemos que las distribuciones de las dos poblaciones son las mismas excepto por un cambio horizontal en la ubicación.
Las hipótesis son:
Ho: las medianas son iguales
Ja: las medianas no son iguales (son posibles pruebas unilaterales)
- Paso 2: Obtener datos, verificar condiciones y resumir datos
(i) Tenemos dos muestras aleatorias independientes. Todas las observaciones en cada muestra deben ser independientes de todas las demás observaciones.
(ii) La versión de la prueba de suma de rangos de Wilcoxon (prueba U de Mann-Whitney) que estamos utilizando asume que la variable de respuesta cuantitativa es una variable aleatoria continua.
(iii) Suponemos que solo hay un turno de ubicación, por lo que debemos verificar que las dos distribuciones sean similares excepto posiblemente por sus ubicaciones.
(iv) Los datos se resumen mediante un estadístico de prueba que cuenta la suma de los rangos de la muestra 1 (o muestra 2).
Para clasificar las observaciones, combinamos todas las observaciones en ambas muestras y clasificamos de menor a mayor.
Luego determinamos qué rangos provienen de la muestra 1 (o muestra 2) y encontramos la suma de estos rangos.
No estarás realizando esta prueba a mano. Simplemente queremos explicar algo de la lógica detrás de escena para estas pruebas.
- Paso 3: Encuentre el valor p de la prueba usando el estadístico de prueba de la siguiente manera
Los valores p se calculan utilizando una distribución específica para esta prueba. Confiaremos en el software para obtener el valor p para esta prueba.
- Paso 4: Conclusión
La decisión se toma de la misma manera que otras pruebas. Podemos expresar nuestra conclusión en términos de las medianas en las dos poblaciones o en términos de la existencia o inexistencia de una relación entre la variable explicativa categórica (X) y la variable respuesta (Y).
OPCIONAL: Para más detalles sobre esta prueba visita La prueba Wilcoxon Rank-Sum de la Escuela de Salud Pública de la Universidad de Boston
Caso CQ — K > 2 — La prueba de Kruskal-Wallis
Analizaremos una prueba no paramétrica en el ajuste de k > 2 muestras independientes.
La prueba de Kruskal-Wallis es una prueba general para comparar múltiples distribuciones en muestras independientes.
La idea detrás de la prueba es determinar si las k poblaciones parecen ser iguales o diferentes en función de los rangos de los valores en lugar de la magnitud. Los procedimientos de clasificación se utilizan comúnmente en métodos no paramétricos, ya que esto modera el efecto de cualquier valor atípico.
La prueba asume distribuciones identicamente conformadas y escaladas para cada grupo, excepto por cualquier diferencia en medianas.
Paso 1: Indicar las hipótesis Las hipótesis son:
- Ho: las medianas de todos los grupos son iguales
- Ja: las medianas no son todas iguales
Paso 2: Obtener datos, verificar condiciones y resumir datos
(i) Tenemos muestras aleatorias independientes de nuestras k poblaciones. Todas las observaciones en cada muestra deben ser independientes de todas las demás observaciones.
(ii) Tenemos una variable de respuesta ordinal, discreta o continua Y.
(iii) Suponemos que solo hay un turno de ubicación por lo que debemos verificar que las distribuciones sean similares excepto posiblemente por sus ubicaciones.
(iv) Los datos se resumen mediante un estadístico de prueba que involucra los rangos de observaciones en cada grupo.
Para clasificar las observaciones, combinamos todas las observaciones en todas las muestras y clasificamos de menor a mayor.
Luego determinamos qué rangos provienen de qué muestra y los usamos para obtener el estadístico de prueba.
Paso 3: Encuentre el valor p de la prueba usando el estadístico de prueba de la siguiente manera
Los valores p se calculan utilizando una distribución específica para esta prueba. Confiaremos en el software para obtener el valor p para esta prueba.
Paso 4: Conclusión
La decisión se toma de la misma manera que otras pruebas. Podemos expresar nuestra conclusión en términos de las medianas en las k poblaciones o en términos de la existencia o inexistencia de una relación entre la variable explicativa categórica (X) y la variable respuesta (Y).
OPCIONAL: Para más detalles sobre esta prueba visita La prueba Kruskal-Wallis de la Escuela de Salud Pública de la Universidad de Boston
Resumimos
- Presentamos la idea básica de las alternativas no paramétricas para el Caso C-Q
- La prueba de signos y la prueba de rango firmado de Wilcoxon son posibles alternativas a la prueba t pareada en el caso de dos muestras dependientes.
- La prueba de suma de rangos de Wilcoxon (también conocida como prueba U de Mann-Whitney) es una posible alternativa a la prueba t de dos muestras en el caso de dos muestras independientes.
- La prueba de Kruskal-Wallis es una posible alternativa al ANOVA unidireccional en el caso de más de dos muestras independientes.
- En este curso, simplemente queremos que seas consciente de qué alternativas no paramétricas se usan comúnmente para abordar problemas con los supuestos.
- No le estamos pidiendo que realice estas pruebas pero seguimos brindando información para aquellos interesados en poder realizar estas pruebas en la práctica.
Envoltorio (Caso C-Q)
Aprende haciendo: Ejemplos y ejercicios suplementarios para la Unidad 4B
(Versión no interactiva)
Precaución
Como mencionamos al final de la Introducción a la Unidad 4B, solo nos centraremos en las pruebas bilaterales para lo que resta de este curso. Las pruebas unilaterales son a menudo posibles, pero rara vez se utilizan en la investigación clínica.
Ya terminamos con el caso C→Q.
- Aprendimos que este caso se clasifica adicionalmente en subcasos, dependiendo del número de grupos que estemos comparando (es decir, el número de categorías que tiene la variable explicativa), y el diseño del estudio (muestras independientes vs. dependientes).
- Para cada uno de los tres subcasos que cubrimos, aprendimos el método inferencial apropiado, y enfatizamos la idea detrás del método, las condiciones bajo las cuales se puede usar de manera segura, cómo llevarlo a cabo usando software y la interpretación de los resultados.
- También aprendimos qué pruebas no paramétricas son aplicables y bajo qué circunstancias podrían usarse en lugar de los métodos estándar.
La siguiente tabla resume cuándo se utilizan cada una de las tres pruebas estándar, cubiertas en este módulo:
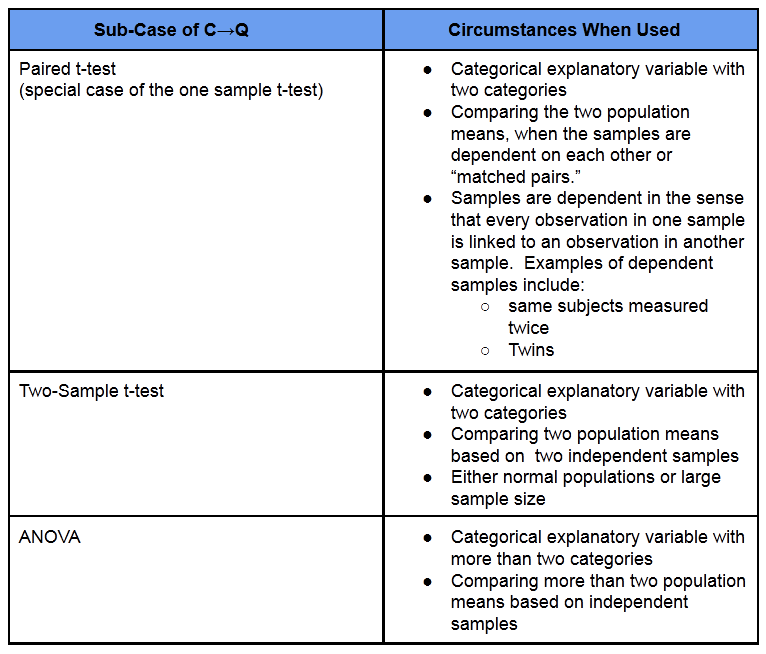
El siguiente resumen analiza cada uno de los subcasos mencionados anteriormente de C→Q dentro del contexto del proceso de prueba de hipótesis.
Paso 1: Declarar las hipótesis nulas y alternativas (H 0 y H a)
- Si bien las alternativas unilaterales se proporcionan aquí siempre que sea posible, recuerde que nos centraremos únicamente en pruebas de doble cara complementadas con intervalos de confianza para los métodos de la Unidad 4B.
0 (igual que H_a: μ_1 > μ_2) * H_a: μ_1 - μ_2 ≠ 0 (igual que H_a: μ_1 ≠ μ_2) Para una prueba t pareada, las hipótesis son H_0: μ_d = 0, y una de: * H_a: μ_d < 0, * H_a: μ_d > 0, * H_0: μ_0 ≠ 0. Para ANOVA, H_0: μ_0 = μ_2 =... = μ_k, y H_A:no todos los μ son iguales” height="311" loading="lazy” src=” http://phhp-faculty-cantrell.sites.m...c-q_table2.png "title="En una prueba t de dos muestras, las hipótesis son: H_0: μ_1 - μ_2 = 0 (o H_0: μ_1 = μ_2), y una de: * _a: μ_1 - μ_2 < 0 (igual que H_a: μ _1 < μ_2) * H_a: μ_1 - μ_2 > 0 (igual que H_a: μ_1 > μ_2) * H_a: μ_1 - μ_2 ≠ 0 (igual que H_a: μ_1 ≠ μ_2) Para una prueba t pareada, las hipótesis son H_0: μ_d = 0, y una de: * H_a: μ_d < 0, * H_a: μ_d > 0, * H_0: μ_0 ≠ 0. Para ANOVA, H_0: μ_0 = μ_2 =... = μ_k, y H_A:no todos los μ son iguales” width="610">
Paso 2: Verifique las condiciones y resuma los datos usando una estadística de prueba
Tenemos que verificar que se cumplan las condiciones bajo las cuales la prueba puede ser utilizada de manera confiable.
Para la prueba t pareada (como caso especial de una prueba t de una muestra), las condiciones son:
- La muestra de diferencias es aleatoria (o al menos puede considerarse así en contexto).
- Estamos en una de las tres situaciones marcadas con una marca de verificación verde en la siguiente tabla:
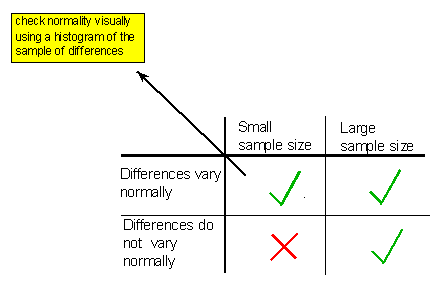
Para la prueba t de dos muestras, las condiciones son:
- Dos muestras son independientes y aleatorias
- Uno de los siguientes dos escenarios se sostiene:
- Ambas poblaciones son normales
- Las poblaciones no son normales, sino de gran tamaño muestral (>30)
Para un ANOVA, las condiciones son:
- Las muestras extraídas de cada una de las poblaciones que se comparan son independientes.
- La variable de respuesta varía normalmente dentro de cada una de las poblaciones que se comparan. Como suele ser el caso, no tenemos que preocuparnos por esta suposición para tamaños de muestra grandes.
- Todas las poblaciones tienen la misma desviación estándar.
Ahora resumimos los datos usando un estadístico de prueba.
- Aunque no estaremos calculando estas estadísticas de prueba a mano, aquí revisaremos las fórmulas para cada estadística de prueba.
Para la prueba t pareada el estadístico de prueba es:
\(t=\dfrac{\bar{y}_{d}-0}{s_{d} / \sqrt{n}}\)
Para la prueba t de dos muestras asumiendo varianzas iguales, el estadístico de prueba es:
\(t=\dfrac{\bar{y}_{1}-\bar{y}_{2}-0}{s_{p} \sqrt{\frac{1}{n_{1}}+\frac{1}{n_{2}}}}\)
donde
\(s_{p}=\sqrt{\dfrac{\left(n_{1}-1\right) s_{1}^{2}+\left(n_{2}-1\right) s_{2}^{2}}{n_{1}+n_{2}-2}}\)
Para la prueba t de dos muestras asumiendo varianzas desiguales el estadístico de prueba es:
\(t=\dfrac{\bar{y}_{1}-\bar{y}_{2}-0}{\sqrt{\frac{s_{1}^{2}}{n_{1}}+\frac{s_{2}^{2}}{n_{2}}}}\)
Para un ANOVA el estadístico de prueba es:

Paso 3: Encontrar el valor p de la prueba
Utilizar software estadístico para determinar el valor p.
- El valor p es la probabilidad de obtener datos como los observados (o incluso más extremos) asumiendo que la hipótesis nula es verdadera, y se calcula usando la distribución nula del estadístico de prueba.
- El valor p es una medida de la evidencia contra H 0.
- Cuanto menor es el valor p, más evidencia presentan los datos contra H 0.
Los valores p para tres pruebas C→Q se obtienen de la salida.
Paso 4: sacar conclusiones
Conclusiones sobre la significancia de los resultados:
- Si el valor p es pequeño, los datos presentan evidencia suficiente para rechazar H o (y aceptar H a).
- Si el valor p no es pequeño, los datos no aportan pruebas suficientes para rechazar H 0.
- Para ayudar a guiar nuestra decisión, utilizamos el nivel de significancia como punto de corte para lo que se considera un valor p pequeño. El punto de corte de significación suele establecerse en .05, pero no debe considerarse inviolable.
Las conclusiones siempre deben formularse en el contexto del problema y todas pueden escribirse en la forma básica a continuación:
- Hay (ES o NO ES) pruebas suficientes de que existe una asociación entre (X) e (Y). Donde X e Y se deben dar en contexto.
Siguiendo la prueba...
- Para una prueba t pareada, un intervalo de confianza del 95% para μ d puede ser muy perspicaz después de que una prueba haya rechazado la hipótesis nula, y también se puede usar para pruebas en el caso bilateral.
- Para una prueba t de dos muestras, un intervalo de confianza del 95% para μ 1 −μ 2 puede ser muy perspicaz después de que una prueba haya rechazado la hipótesis nula, y también se puede usar para pruebas en el caso bilateral.
- Si la prueba F de ANOVA ha rechazado la hipótesis nula, observar los intervalos de confianza para las medias poblacionales que están en la salida puede proporcionar una idea visual de por qué se rechazó el H 0 (es decir, cuál de las medias difiere).
Alternativas no paramétricas
- Para una prueba de t pareada podríamos investigar usando la prueba de rango firmado de Wilcoxon o la prueba de signo.
- Para una prueba t de dos muestras podríamos investigar usando la prueba de Wilcoxon Rank-Sum (prueba U de Mann-Whitney).
- Para un ANOVA podríamos investigar usando la prueba de Kruskal-Wallis.

