5.4: Regla de Complemento
- Page ID
- 151824
A veces es difícil calcular la probabilidad de que ocurra un evento, pero es mucho más fácil calcular la probabilidad de que no ocurra un evento.
Por ejemplo, es posible que desee determinar la probabilidad de que un estudiante de la Universidad Estatal de California — East Bay se comente en algo que no sea Negocios. En lugar de sumar todas las probabilidades mayores no comerciales, sería mucho más fácil encontrar la oportunidad de que un estudiante en CSUEB se gradúe en Negocios, digamos 21%. Entonces determinarías que la probabilidad de que un estudiante no se gradee en Negocios (todos los demás estudiantes) es el 79% restante.
Regla de Complemento
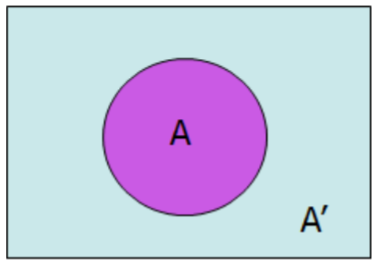
A' (leído como “complemento A”) es el evento en el que el evento A no ocurre. En ese caso, la Regla del Complemento es:
\[P(A)+P\left(A^{\prime}\right)=1 \quad P(A)=1-P\left(A^{\prime}\right) \quad P\left(A^{\prime}\right)=1-P(A) \nonumber \]
Ejemplo: Troquelado
En un juego, debes seguir rodando un dado de seis caras hasta conseguir un seis. ¿Cuál es la probabilidad de que necesites 2 o más rollos para conseguir un seis?
Solución
El evento A es “2 o más rollos para obtener un seis” que sería una probabilidad muy difícil de calcular ‐‐ en realidad es una suma infinita!
El evento A' es “no tomes 2 o más rollos para conseguir un seis” que es lo mismo que decir “consigue un seis en el primer rollo”. Esa es una probabilidad mucho más fácil de calcular,\(P\left(A^{\prime}\right)=1 / 6\).
Entonces\(P(A)=1-P\left(A^{\prime}\right)=1-1 / 6=5 / 6\)
Por lo tanto, la probabilidad de necesitar dos o más rollos para obtener un seis es 5/6 o aproximadamente 83.3%


