5.3: Cómo calcular la probabilidad clásica
- Page ID
- 151823
Podemos usar métodos de conteo para determinar la probabilidad clásica. Sin embargo, debemos tener cuidado en nuestros métodos para asegurarnos de obtener la respuesta correcta.
Un Evento es el resultado de un experimento, generalmente referido con mayúscula A, B, C, etc. Considere el experimento de voltear dos monedas. Después usa la letra A para hacer referencia al evento de obtener exactamente una cabeza.
Un resultado es un resultado del experimento que no se puede descomponer en eventos más pequeños. Considera el evento A, obteniendo exactamente una cabeza. Tenga en cuenta que hay dos formas o resultados para obtener una cabeza en dos tiradas, primero obteniendo una cabeza luego una cola, o primero obteniendo una cola, luego una cabeza. Escribamos estos resultados distintos como HT y TH.
El espacio de muestra es el conjunto de todos los resultados posibles de un experimento. En el experimento de voltear dos monedas, hay 4 posibles resultados, los cuales se pueden expresar en notación fija.
\[\text { Sample Space }=\{\mathrm{HH}, \mathrm{HT}, \mathrm{TH}, \mathrm{TT}\} \nonumber \]
Ahora podemos redefinir un Evento de un experimento para que sea un subconjunto del Espacio de Muestra. Si el evento A recibe exactamente una cabeza en dos tiradas de monedas, entonces
\[\mathrm{A}=\{\mathrm{HT}, \mathrm{TH}\}\nonumber \]
Después de enumerar cuidadosamente los resultados del Espacio de Muestra y los resultados del evento, podemos calcular la probabilidad de que ocurra el evento.
Probabilidad Evento Ocurre = número de resultados en el Evento/número de resultados en el Espacio de Muestra
Utilizaremos la notación P (A) para significar que ocurre el evento de probabilidad A.
En el ejemplo, la probabilidad de obtener exactamente 1 cabeza en dos tiradas de monedas es de 2 de 4 o 50%. \[P(A)=2 / 4=0.5=50 \% \nonumber \]
Ejemplo: Apuesta de campo
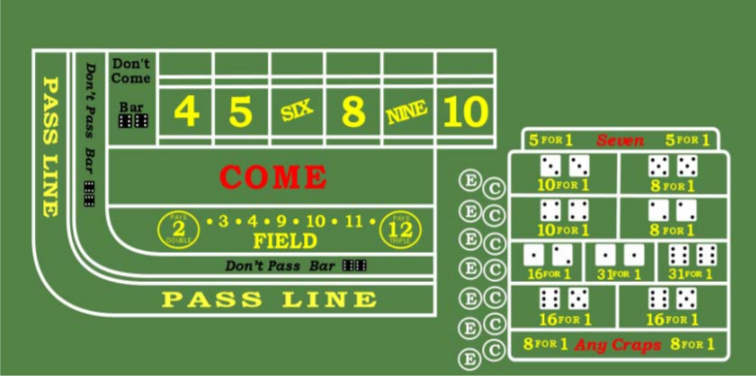
En el juego de dados de casino, se tiran dos dados al mismo tiempo y luego se suman los dos números resultantes. Hay muchas apuestas en los dados, así que consideremos la apuesta Field. En esta apuesta, el jugador ganará incluso dinero si se rueda un total de 3, 4, 9, 10 o 11. Si se rueda un total de 2, el jugador ganará el doble de la apuesta original, y si se rueda un total de 12, el jugador ganará el triple de la apuesta original. Si se rueda un total de 5, 6, 7 u 8, el jugador pierde la apuesta original.
A primera vista, esto parece una apuesta ganadora para el jugador ya que el jugador gana en 7 números diferentes y el casino solo gana en 4 números diferentes. No obstante, sabemos que un casino siempre diseña juegos para darle ventaja al casino. Usemos cuidadosamente los métodos de conteo para calcular la probabilidad de que un jugador gane la apuesta Field.

Primero consideremos la tarea de enumerar el espacio muestral de posibles resultados. Dado que hay dos dados tirados, podemos considerar que cada resultado es un par ordenado. Hay 6 valores posibles para el primer dado y 6 valores posibles para el segundo dado, lo que significa que hay 36 pares ordenados o resultados. En el diagrama, el dado rojo es el primer rollo y el dado verde es el segundo rollo.
\ [\ text {Espacio de muestra} =\ left\ {\ begin {array} {l}
(1,1), (1,2), (1,3), (1,4), (1,5), (1,6),\\
(2,1), (2,2), (2,3), (2,4), (2,5), (2,6),\\
(3,1), (3,2), (3,3), (3,4), (3,5), (3,6),\\
(4,1), (4,2), (4,3), (4,4), (4,5), (4,6),\\
(5,1), (5,2), (5,3), (5,4), (5,5), (5,6),\\
(6,1), (6,2), (6,3), (6,4), (6,5), (6,6)
\ end {array}\ derecha\}\ nonumber\]
Ahora definen el evento W para que sean los pares ganadores de números en la apuesta de Campo, los pares que suman 2, 3, 4, 9, 10, 11 o 12. Los pares ganadores de números se muestran en azul y los pares perdedores se muestran en rojo.
\ [\ text {Espacio de muestra} =\ left\ {\ begin {array} {l}
(1,1), (1,2), (1,3), (1,4), (1,5), (1,6),\\
(2,1), (2,2), (2,3), (2,4), (2,5), (2,6),\\
(3,1), (3,2), (3,3), (3,4), (3,5), (3,6),\\
(4,1), (4,2), (4,3), (4,4), (4,5), (4,6),\\
(5,1), (5,2), (5,3), (5,4), (5,5), (5,6),\\
(6,1), (6,2), (6,3), (6,4), (6,5), (6,6)
\ end {array}\ derecha\}\ quad W=\ izquierda\ {\ comenzar {matriz} {l}
(1,1), (1,2), (1,3),\\
(2,1), (2,2),\
(3,1), (3,6),\\
(4,5), (4,6),\\
(5,4), (5,5), (5,6),\\
(6,3), (6,4), (6,5), (6,6)
\ end {array}\ derecha\}\ nonumber\]
Esto significa que hay 16 resultados de 36 en los que gana el jugador. Ahora es fácil ver que esa probabilidad de ganar es inferior al 50%, ya que el casino se llevó los números que ocurren con más frecuencia.
\[P(W)=\frac{16}{36}=\frac{4}{9} \approx 44.4 \% \nonumber \]
Como nota final sobre este ejemplo, tal vez recuerdes que el casino paga el doble si el jugador rueda (1,1) o el triple si el jugador rueda (6,6). Incluso teniendo en cuenta este bono extra, si un jugador hace 36 apuestas de $100, el casino esperará ganar $2000 (20 números x $100), y el jugador esperará ganar $1900 (16 números x $100, más $100 adicionales para el 2 y $200 extra por el 12), lo que significa que el jugador pierde $100 por cada apuesta de $3600, una casa (casino) ventaja de 2.78%.
| Apuesta de Campo — Resumen de 36 rollos posibles | Cantidad ganada en apuestas de $100 |
|---|---|
| \((1,1)\)(paga el doble) | +$200 |
| \((6,6)\)(paga triple) | +$300 |
| \((1,2),(1,3),(2,1),(2,2),(3,1),(3,6),(4,5),(4,6),(5,4),(5,5),(5,6),(6,3),(6,4),(6,5)\) | +$1400 |
| \((1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,2),(3,3),(3,4),(3,5),(4,1),(4,2),(4,3),(4,4),(5,1),(5,2),(5,3),(6,1),(6,2)\) | ‐$2000 |
| Resultado general esperado de 36 rollos (apuesta $3600) | ‐$100 |
Solo recuerda, a la larga, el casino siempre gana.


