15.2.10: Capítulo 11 Tarea
- Page ID
- 151474
- ¿Cuál es la diferencia entre dos muestras que son dependientes y dos muestras que son independientes? Dé un ejemplo de dos muestras dependientes y dos muestras independientes.
- ¿Qué condiciones son necesarias para utilizar la prueba t de muestras dependientes para la media de la diferencia de dos poblaciones?
En Problemas 3‐10, clasifique las dos muestras dadas como independientes o dependientes. Explica tu razonamiento.
- Muestra 1: El SAT puntúa para 35 estudiantes de secundaria que no tomaron un curso de preparación del SAT; Muestra 2: El SAT puntúa para 40 estudiantes de secundaria que sí tomaron un curso de preparación para el SAT
- Muestra 1: El SAT puntúa para 44 estudiantes de secundaria; Muestra 2: El SAT puntúa para los mismos 44 estudiantes de secundaria después de tomar un curso de preparación para el SAT
- Muestra 1: Los pesos de 51 adultos; Muestra 2: Los pesos de los mismos 51 adultos después de participar en un programa de dieta y ejercicio durante un mes
- Muestra 1: Los pesos de 40 hembras; Muestra 2: Los pesos de 40 machos
- Muestra 1: La velocidad promedio de 23 lanchas con un diseño de casco antiguo; Muestra 2: La velocidad promedio de 14 lanchas con un nuevo diseño de casco
- Muestra 1: El kilometraje de combustible de 10 autos; Muestra 2: El kilometraje de combustible de los mismos 10 autos usando un aditivo de combustible
- La tabla muestra las distancias de frenado (en pies) para cada uno de los cuatro juegos diferentes de llantas con el sistema de frenos antibloqueo (ABS) del automóvil encendido y con ABS apagado. Las pruebas se realizaron sobre hielo con autos que viajaban a 15 millas por hora.
| Juego de Llantas | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Distancia de frenado con ABS | 42 | 55 | 43 | 61 |
| Distancia de frenado sin ABS | 58 | 67 | 59 | 75 |
- En la tabla se muestran las frecuencias cardíacas (en latidos por minuto) de cinco personas antes y después de hacer ejercicio.
| Persona | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Frecuencia cardíaca antes de hacer ejercicio | 42 | 55 | 43 | 61 | 65 |
| Frecuencia cardíaca después de hacer ejercicio | 58 | 67 | 59 | 75 | 90 |
- En un estudio que probó los efectos de un suplemento herbario sobre la presión arterial DATA en hombres, 11 hombres seleccionados al azar recibieron un suplemento herbario durante 15 semanas. Las siguientes mediciones son para la presión arterial diastólica de cada sujeto tomadas antes y después del periodo de tratamiento de 15 semanas. En\(\alpha=.10\), ¿se puede apoyar la afirmación de que se bajó la presión arterial sistólica?

- Una muestra aleatoria de 25 tiempos de espera (en minutos) antes de que los pacientes atendieran a un profesional médico en el servicio de urgencias menores de un hospital tuvieron una desviación estándar de 0.7 minutos. Después de implementar un nuevo procedimiento de admisión, una muestra aleatoria de 21 tiempos de espera tuvo una desviación estándar de 0.5 minutos. En\(\alpha=.10\), ¿puedes apoyar la afirmación del hospital de que la desviación estándar de los tiempos de espera ha disminuido?

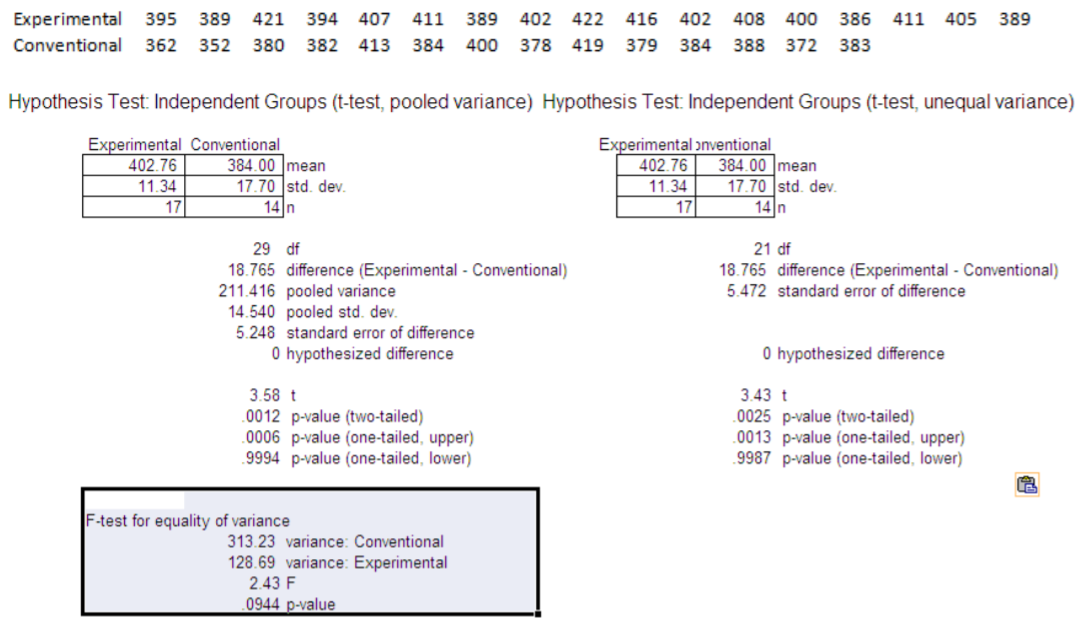
- Un ingeniero quiere comparar las resistencias a la tracción de las barras de acero que se producen utilizando un método convencional y un método experimental. (La resistencia a la tracción de un metal es una medida de su capacidad para resistir el desgarro cuando se tira longitudinalmente). Para ello, el ingeniero selecciona aleatoriamente barras de acero que se fabrican utilizando cada método y registra las siguientes resistencias a la tracción (en Newtons por milímetro cuadrado). En\(\alpha=.10\), ¿puede el ingeniero afirmar que el método experimental produce acero con mayor resistencia media a la tracción? ¿El ingeniero debería recomendar utilizar el método experimental? Primero use la\(F\) prueba para determinar si usar o no varianzas iguales en la elección del modelo.

- Un colegio comunitario está considerando usar múltiples medidas para la colocación de estudiantes en cursos de matemáticas. La medida existente es que cada alumno realice un examen de colocación estandarizado. Con base en la puntuación, el alumno será colocado en uno de los tres cursos de matemáticas: Nivel Primaria, Nivel Intermedio y Nivel de Transferencia. Una segunda medida consistirá en utilizar el GPA de preparatoria para modificar el puntaje de examen de colocación necesario para cada uno de los tres cursos.
200 estudiantes entrantes que tienen GPA de secundaria se dividieron aleatoriamente en dos grupos. Al primer grupo de 100 alumnos se le dio el examen de colocación existente únicamente. El segundo grupo de 100 alumnos se colocó utilizando la nueva segunda medida que utiliza tanto los exámenes de colocación como los GPA de secundaria.
Después de tres cuartas partes, se encontró que 17 del primer grupo completaron el curso Nivel de Transferencia mientras que 31 del segundo grupo completaron el curso Nivel de Transferencia. Con base en este resultado, el investigador decidió que el nuevo método de múltiples medidas para colocar a los estudiantes mejoró el porcentaje de estudiantes que aprueban el curso de matemáticas Nivel de Transferencia en tres trimestres.



