15.2.11: Capítulo 12 Tarea
- Page ID
- 151410
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
- Una organización de seguridad de bicicletas afirma que los accidentes fatales de bicicleta se distribuyen uniformemente a lo largo de la semana En la tabla se muestra el día de la semana para el que ocurrieron 911 accidentes fatales de bicicleta seleccionados al azar. En\(\alpha = 0.10\), ¿puede rechazar la afirmación de que la distribución es uniforme?
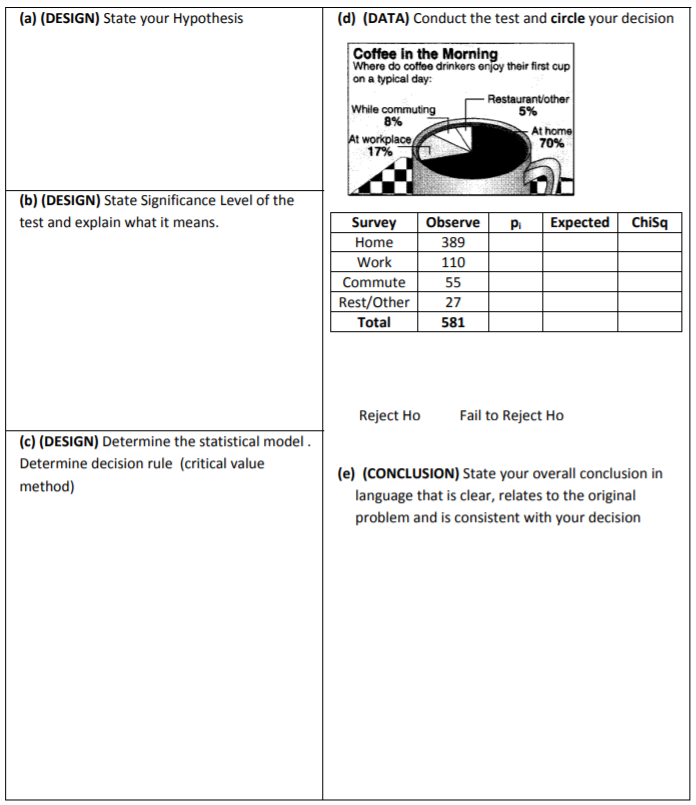
- Los resultados de una encuesta de cinco años preguntaron dónde los bebedores de café suelen tomar su primera taza de café se muestran en la gráfica. Para determinar si esta distribución ha cambiado, seleccionas al azar 581 bebedores de café y les preguntas dónde suelen tomar su primera taza de café. Los resultados se muestran en la tabla. ¿Se puede concluir que ha habido un cambio en la distribución reclamada o esperada? Uso\(\alpha = 0.05\).
- En una encuesta de SurveyUSA, se preguntó a 500 adultos estadounidenses si se debía legalizar la marihuana. Los resultados de la encuesta fueron tabulados de manera cruzada como se muestra en las tablas de contingencia a continuación. Realizar una prueba de hipótesis de independencia para determinar si la opinión sobre la legalización de la marihuana depende de la edad.
| Macho | Hembra | |
| Debe ser Legal | 123 | 90 |
| No debe ser legal | 127 | 160 |
- En una encuesta de SurveyUSA, se preguntó a 500 adultos estadounidenses si se debía legalizar la marihuana. Los resultados de la encuesta fueron tabulados de manera cruzada como se muestra en las tablas de contingencia a continuación. Realizar una prueba de hipótesis de independencia para determinar si la opinión sobre la legalización de la marihuana depende del género.
| 18‐34 | 35‐54 | 55+ | |
| Debe ser Legal | 95 | 83 | 48 |
| No debe ser legal | 65 | 126 | 83 |
- Recientemente se encuestó a 1000 adultos estadounidenses sobre su opinión sobre el efecto del reciente proyecto de ley de estímulo y la economía. Los resultados se muestran en la siguiente tabla de contingencias, desglosados por género:
| Estímulo perjudicará economía | Estímulos ayudarán a la economía | El estímulo no tendrá efecto | TOTAL | |
| Macho | 150 | 150 | 200 | 500 |
| Hembra | 100 | 200 | 200 | 500 |
| TOTAL | 250 | 350 | 400 | 1000 |
¿El género y la opinión sobre los estímulos son variables dependientes? Prueba usando\(\alpha =1\%\).
Para los estudios en las preguntas 6 a 8, conteste las siguientes preguntas. (En realidad no tendrás que realizar pruebas).
- Exponer las hipótesis nulas y alternativas en palabras
- Anotar las Hipótesis Nulas y Alternativas en parámetros poblacionales
- Elija el modelo apropiado de entre estos tres:
- Una prueba poblacional de proporción
- La bondad de ajuste de Chi‐cuadrado
- Prueba de independencia de Chi‐cuadrado
- A partir de 2018, el Sistema Universitario Estatal de California (CSU) cambió sus requisitos previos para un curso de Estadística necesario para que los estudiantes de colegios comunitarios se transfieran. La disposición original era que los estudiantes necesitaban tomar Álgebra Intermedia antes de Estadística. El nuevo requisito es que los estudiantes puedan tomar Álgebra Intermedia o una ruta alternativa al curso de Estadística como requisito previo para la Estadística. Existe cierta preocupación de que los estudiantes que eligen la ruta alternativa puedan tener menos éxito después de transferirse a CSU. Se propone un estudio para determinar las tasas de egreso en 3 años para los estudiantes transferidos que aprobaron Álgebra Intermedia y aquellos que aprobaron el curso alternativo. Los datos serán recolectados y tabulados cruzados en dos preguntas: “¿Qué camino escogió el alumno?” y “¿El alumno se graduó dentro de los 3 años posteriores al traslado?”
- El tendón de Aquiles conecta el músculo de la pantorrilla al hueso del talón. De los pacientes que rompieron (desgarran) el tendón de Aquiles y lo reparan quirúrgicamente, 11% volverán a romper el tendón de Aquiles dentro de los tres años posteriores al tratamiento. Un método de tratamiento no quirúrgico propuesto trataría la ruptura con una serie de moldes, ultrasonido y movimiento pasivo. El investigador quiso demostrar que el porcentaje de pacientes que eligen el método de tratamiento no quirúrgico tuvo un porcentaje reducido de rerupturas.
- Una empresa de calzado deportivo ha diseñado una zapatilla para correr para mujer y está considerando producir la zapatilla en 4 colores diferentes: rosa, azul, verde azulado y gris. La compañía quiere saber si existe preferencia entre las mujeres por un color específico del zapato. En el estudio participarán 154 mujeres que son corredores.


