7.1: Funciones de distribución y densidad
- Page ID
- 151024
En la unidad sobre Variables Aleatorias y Probabilidad introducimos variables aleatorias reales como mapeos desde el espacio básico\(\Omega\) a la línea real. El mapeo induce una transferencia de la masa de probabilidad en el espacio básico a subconjuntos de la línea real de tal manera que la probabilidad que\(X\) toma un valor en un conjunto\(M\) es exactamente la masa asignada a ese conjunto por la transferencia. Para realizar cálculos de probabilidad, necesitamos describir analíticamente la distribución en la línea. Para variables aleatorias simples esto es fácil. Tenemos en cada valor posible de\(X\) un punto de masa igual a la probabilidad\(X\) toma ese valor. Para casos más generales, necesitamos una descripción más útil que la proporcionada por la medida de probabilidad inducida\(P_X\).
La función de distribución
En la discusión teórica sobre Variables Aleatorias y Probabilidad, observamos que la distribución de probabilidad inducida por una variable aleatoria\(X\) se determina de manera única por una asignación consistente de masa a intervalos semi-infinitos de la forma\((-\infty, t]\) para cada real\(t\). Esto sugiere que una descripción natural es proporcionada por lo siguiente.
Definición
La función de distribución\(F_X\) para la variable aleatoria\(X\) viene dada por
\(F_X(t) P(X \le t) = P(X \in (-\infty, t])\)\(\forall t \in R\)
En términos de la distribución de masa en la línea, esta es la masa de probabilidad en o a la izquierda del punto t. Como consecuencia,\(F_X\) tiene las siguientes propiedades:
- (F1):\(F_X\) debe ser una función no decreciente, pues si debe\(t > s\) haber al menos tanta masa probabilística a o a la izquierda de\(t\) como haya para\(s\).
- (F2):\(F_X\) es continuo desde la derecha, con un salto en la cantidad\(p_0\) a\(t_0\) iff\(P(X = t_0) = p_0\). Si el punto\(t\) se\(t_0\) aproxima desde la izquierda, el intervalo no incluye la masa de probabilidad a\(t_0\) hasta que\(t\) alcanza ese valor, momento en el que la cantidad a o a la izquierda de t aumenta (“salta”) por cantidad\(p_0\); por otro lado, si\(t\) se acerca\(t_0\) desde la derecha, el intervalo incluye la masa\(p_0\) hasta e incluyendo\(t_0\), pero cae inmediatamente a medida que\(t\) se mueve a la izquierda de\(t_0\).
- (F3): Excepto en casos muy inusuales que involucren variables aleatorias que puedan tomar valores “infinitos”, la masa de probabilidad incluida en\((-\infty, t]\) debe aumentar a uno a medida que t se mueve hacia la derecha; cuando\(t\) se mueve hacia la izquierda, la masa de probabilidad incluida debe disminuir a cero, de manera que \[F_X(-\infty) = \lim_{t \to - \infty} F_X(t) = 0\]y\[F_X(\infty) = \lim_{t \to \infty} F_X(t) = 1\]
Una función de distribución determina la masa de probabilidad en cada intervalo semiinfinito\((\infty, t]\). De acuerdo con la discusión referida anteriormente, esto determina de manera única la distribución inducida.
La función de distribución\(F_X\) para una variable aleatoria simple se visualiza fácilmente. La distribución consiste\(p_i\) en masa puntual en cada punto\(t_i\) del rango. A la izquierda del valor más pequeño en el rango,\(F_X(t) = 0\); a medida que t aumenta al valor más pequeño\(t_1\),\(F_X(t)\) permanece constante en cero hasta que salta por la cantidad\(p_1\)... \(F_X(t)\)permanece constante en\(p_1\) hasta que\(t\) aumenta a\(t_2\), donde salta por una cantidad p 2 al valor\(p_1 + p_2\). Esto continúa hasta que el valor de\(F_X(t)\) alcanza 1 en el valor más grande\(t_n\). La gráfica de\(F_X\) es así una función de paso, continua desde la derecha, con un salto en la cantidad\(p_i\) en el punto correspondiente\(t_i\) en el rango. Una situación similar existe para una variable aleatoria de valor discreto que puede tomar infinidad de valores (por ejemplo, la distribución geométrica o la distribución de Poisson considerada a continuación). En este caso, siempre hay alguna probabilidad en los puntos a la derecha de cualquiera\(t_i\), pero ésta debe volverse vertiginosamente pequeña a medida que\(t\) aumenta, ya que la masa de probabilidad total es una.
El procedimiento ddbn se puede utilizar para trazar la función de distribución para una variable aleatoria simple a partir de una matriz X de valores y una matriz correspondiente PX de probabilidades.
Ejemplo\(\PageIndex{1}\): Graph of FX for a simple random variable
>> c = [10 18 10 3]; % Distribution for X in Example 6.5.1 >> pm = minprob(0.1*[6 3 5]); >> canonic Enter row vector of coefficients c Enter row vector of minterm probabilities pm Use row matrices X and PX for calculations Call for XDBN to view the distribution >> ddbn % Circles show values at jumps Enter row matrix of VALUES X Enter row matrix of PROBABILITIES PX % Printing details See Figure 7.1

Descripción de algunas distribuciones discretas comunes
Hacemos uso repetido de una serie de distribuciones comunes que se utilizan en muchas situaciones prácticas. Esta colección incluye varias distribuciones las cuales se estudian en el capítulo "Variables y Probabilidades Aleatorias”.
Función de indicador. \(X = I_E P(X = 1) = P(E) = pP(X = 0) = q = 1 - p\). La función de distribución tiene un salto en la cantidad\(q\) en\(t = 0\) y un salto adicional de\(p\) al valor 1 at\(t = 1\).
Variable aleatoria simple\(X = \sum_{t_i} I_{A_i}\) (forma canónica)
La función de distribución es una función de paso, continua desde la derecha, con salto de\(p_i\) at\(t = t_i\) (Ver Figura 7.1.1 para el Ejemplo 7.1.1)
Binomial (\(n, p\)). Esta variable aleatoria aparece como el número de éxitos en una secuencia de ensayos de\(n\) Bernoulli con probabilidad\(p\) de éxito. En su forma más simple
\(X = \sum_{i = 1}^{n} I_{E_i}\)con\(\{E_i: 1 \le i \le n\}\) independiente
\(P(E_i) = p\)\(P(X = k) = C(n, k) p^k q^{n -k}\)
Como se señaló en el estudio de las secuencias de Bernoulli en la unidad de Ensayos Compuestos, se dispone de dos funciones m ibinom y cbinom para calcular las probabilidades binomiales individuales y acumulativas.
Geométricas (\(p\)) Hay dos distribuciones relacionadas, ambas surgidas en el estudio de secuencias continuas de Bernoulli. El primero cuenta el número de fracasos antes del primer éxito. Esto a veces se llama el “tiempo de espera”. El evento {\(X = k\)} consiste en una secuencia de\(k\) fracasos, luego un éxito. Así
El segundo designa el ensayo componente en el que se produce el primer éxito. El evento {\(Y = k\)} consiste en\(k - 1\) fallas, luego un éxito en la prueba de componentes\(k\) th. Tenemos
Decimos\(X\) tiene la distribución geométrica con parameter (\(p\)), que a menudo designamos por\(X~\) geometric (\(p\)). Ahora\(Y = X + 1\) o\(Y - 1 = X\). Por ello, se acostumbra referirse a la distribución para el número del ensayo para el primer éxito diciendo\(Y - 1 ~\) geométrico (\(p\)). La probabilidad de\(k\) o más fracasos antes del primer éxito es\(P(X \ge k) = q^k\). También
Esto sugiere que una secuencia de Bernoulli esencialmente “comienza de nuevo” en cada juicio. Si ha fracasado\(n\) veces, la probabilidad de fallar una\(k\) o más veces adicionales antes del siguiente éxito es la misma que la probabilidad inicial de fallar\(k\) o más veces antes del primer éxito.
Ejemplo\(\PageIndex{2}\): The geometric distribution
Un estadístico está tomando una muestra aleatoria de una población en la que dos por ciento de los integrantes poseen un automóvil BMW. Toma una muestra de talla 100. ¿Cuál es la probabilidad de no encontrar propietarios de BMW en la muestra?
Solución
El proceso de muestreo puede ser visto como una secuencia de ensayos de Bernoulli con probabilidad\(p = 0.02\) de éxito. La probabilidad de 100 o más fracasos antes del primer éxito es\(0.98^{100} = 0.1326\) o alrededor de 1/7.5.
Binomial negativo (\(m, p\)). \(X\)es el número de fracasos antes del éxito\(m\) th. Generalmente es más conveniente trabajar con\(Y = X + m\), el número del juicio en el que se produce el éxito\(m\) th. Un examen de los posibles patrones y combinatorias elementales muestran que
Hay m —1 éxitos en los primeros\(k - 1\) ensayos, luego un éxito. Cada combinación tiene probabilidad\(p^m q^{k - m}\). Tenemos una función m nbinom para calcular estas probabilidades.
Ejemplo\(\PageIndex{3}\): A game of chance
Un jugador lanza repetidamente un solo dado de seis lados. Apunta si lanza un 1 o un 6. ¿Cuál es la probabilidad de que anote cinco veces en diez lanzamientos o menos?
>> p = sum(nbinom(5,1/3,5:10)) p = 0.2131
Una solución alternativa es posible con el uso de la distribución binomial. El\(m\) éxito llega a más tardar en el k th juicio si el número de éxitos en los\(k\) ensayos es mayor o igual a\(m\).
>> P = cbinom(10,1/3,5) P = 0.2131
Poisson (\(\mu\)). Esta distribución se asume en una amplia variedad de aplicaciones. Aparece como una variable de conteo para los ítems que llegan con tiempos de interllegada exponenciales (ver la relación con la distribución gamma a continuación). Para grandes\(n\) y pequeños\(p\) (que puede no ser un valor que se encuentra en una tabla), la distribución binomial es aproximadamente de Poisson (\(np\)). El uso de la función generadora (ver Métodos de transformación) muestra que la suma de variables aleatorias independientes de Poisson es Poisson. La distribución de Poisson es de valor entero, con
Aunque las probabilidades de Poisson suelen ser más fáciles de calcular con calculadoras científicas que las probabilidades binomiales, el uso de tablas suele ser bastante útil. Como en el caso de la distribución binomial, tenemos dos funciones m para calcular las probabilidades de Poisson. Estos tienen ventajas de velocidad y rango de parámetros similares a los de ibinom y cbinom.
\(P(X = k)\)se calcula por P = ipoisson (mu, k), donde\(k\) es un vector de fila o columna de enteros y el resultado\(P\) es una matriz de filas de las probabilidades.
\(P(X \ge k)\)se calcula por P = cpoisson (mu, k), donde\(k\) es un vector de fila o columna de enteros y el resultado\(P\) es una matriz de filas de las probabilidades.
Ejemplo\(\PageIndex{4}\): Poisson counting random variable
El número de mensajes que llegan en un periodo de un minuto a un cruce de red de comunicaciones es una variable aleatoria N ∼ Poisson (130). ¿Cuál es la probabilidad de que el número de llegadas sea mayor que igual a 110, 120, 130, 140, 150, 160?
>> p = cpoisson(130,110:10:160) p = 0.9666 0.8209 0.5117 0.2011 0.0461 0.0060
Las descripciones de estas distribuciones, junto con una serie de otros hechos, se resumen en la tabla DATOS SOBRE ALGUNAS DISTRIBUCIONES COMUNES en el Apéndice C.
La función de densidad
Si la masa de probabilidad en la distribución inducida se extiende suavemente a lo largo de la línea real, sin concentraciones de masa puntual, existe una función de densidad de probabilidad\(f_X\) que satisface
\(P(X \in M) = P_X(M) = \int_M f_X(t)\ dt\)(están debajo de la gráfica de\(f_X\) más\(M\))
En cada uno\(t\),\(f_X(t)\) es la masa por unidad de longitud en la distribución de probabilidad. La función de densidad tiene tres propiedades características:
(f1)\(f_X \ge 0\) (f2)\(\int_R f_X = 1\) (f3)\(F_X (t) = \int_{-\infty}^{t} f_X\)
Una variable aleatoria (o distribución) que tiene una densidad se llama absolutamente continua. Este término proviene de la teoría de medidas. A menudo simplemente abreviamos como distribución continua.
- Existe una descripción matemática técnica de la condición “diseminada suavemente sin concentraciones puntuales de masa”. Y estrictamente hablando las integrales son integrales de Lebesgue más que del tipo ordinario de Riemann. Pero para casos prácticos, los dos están de acuerdo, de manera que somos libres de utilizar técnicas de integración ordinarias.
- Por el teorema fundamental del cálculo
\(f_X(t) = F_X^{'} (t)\)en cada punto de continuidad de\(f_X\)
- Cualquier función integrable, no negativa\(f\) con\(\int f = 1\) determina una función de distribución\(F\), que a su vez determina una distribución de probabilidad. Si\(\int f \ne 1\), la multiplicación por la constante positiva apropiada da un adecuado\(f\). Un argumento basado en la Función Cuantile muestra la existencia de una variable aleatoria con esa distribución.
- En la literatura sobre probabilidad, se acostumbra omitir la indicación de la región de integración al integrarse sobre toda la línea. Así
\(\int g(t) f_X (t) dt = \int_R g(t) f_X(t) dt\)
La primera expresión no es una integral indefinida. En muchas situaciones,\(f_X\) será cero fuera de un intervalo. Así, el integrando determina efectivamente la región de integración.

Algunas distribuciones comunes absolutamente continuas
Uniforme\((a, b)\).
La masa se extiende uniformemente en el intervalo\([a, b]\). Es inmaterial si se incluyen o no los puntos finales, ya que la probabilidad asociada a cada punto individual es cero. La probabilidad de cualquier subintervalo es proporcional a la longitud del subintervalo. La probabilidad de estar en dos subintervalos cualesquiera de la misma longitud es la misma. Esta distribución se utiliza para modelar situaciones en las que se sabe que\(X\) toma valores en\([a, b]\) pero es igualmente probable que estén en cualquier subintervalo de una longitud dada. La densidad debe ser constante a lo largo del intervalo (cero afuera), y la función de distribución aumenta linealmente con\(t\) en el intervalo. Por lo tanto,
La gráfica de\(F_X\) sube linealmente, con pendiente 1/ (\(b - a\)) de cero\(t = a\) a uno at\(t = b\).
Triangular simétrico\((-a, a)\),\(f_X(t) = \begin{cases} (a + t)/a^2 & -a \le t < 0 \\ (a - t)/a^2 & 0 \le t \le a \end{cases}\).
Esta distribución se usa frecuentemente en ejemplos numéricos instruccionales porque las probabilidades se pueden obtener geométricamente. Se puede desplazar, con un desplazamiento de la gráfica, a diferentes conjuntos de valores. Aparece naturalmente (en forma desplazada) como la distribución para la suma o diferencia de dos variables aleatorias independientes distribuidas uniformemente en intervalos de la misma longitud. Este hecho se establece con el uso de la función generadora de momento (ver Métodos de transformación). De manera más general, la densidad puede tener una gráfica triangular que no es simétrica.
Ejemplo\(\PageIndex{5}\): Use of a triangular distribution
Supongamos\(X~\) simétrico triangular (100, 300). Determinar\(P(120 < X \le 250)\).
Observación. Tenga en cuenta que en el caso continuo, es inmaterial si se incluye o no el punto final de los intervalos.
Solución
Para obtener el área debajo del triángulo entre 120 y 250, tomamos uno menos el área de los triángulos rectos entre 100 y 120 y entre 250 y 300. Usando el hecho de que áreas de triángulos similares son proporcionales al cuadrado de cualquier lado, tenemos
\(P = 1 - \dfrac{1}{2} ((20/100)^2 + (50/100)^2) = 0.855\)
Exponencial (\(\lambda\))\(f_X(t) = \lambda e^{-\lambda t}\)\(t \ge 0\) (cero en otra parte).
La integración muestra\(F_X(t) = 1 - e^{-\lambda t}\) (t\ ge 0\) (cero en otra parte). Tomamos nota de eso\(P(X > 0) = 1 - F_X(t) = e^{-\lambda t}\)\(t \ge 0\). Esto lleva a una propiedad extremadamente importante de la distribución exponencial. Ya que\(X > t + h\)\(X > t\),\(h > 0\) implica, tenemos
Debido a esta propiedad, la distribución exponencial se utiliza a menudo en problemas de confiabilidad. Supongamos que\(X\) representa el tiempo hasta el fallo (es decir, la duración de la vida) de un dispositivo puesto en servicio en\(t = 0\). Si la distribución es exponencial, esta propiedad dice que si el dispositivo sobrevive al tiempo\(t\) (es decir,\(X > t\)) entonces la probabilidad (condicional) de que sobreviva a\(h\) más unidades de tiempo es la misma que la probabilidad original de sobrevivir por\(h\) unidades de tiempo. Muchos aparatos tienen la propiedad que no se desgastan. El fracaso se debe a algún estrés de origen externo. Muchos dispositivos electrónicos de estado sólido se comportan esencialmente de esta manera, una vez que las pruebas iniciales de “quemado” han eliminado las unidades defectuosas. El uso de la ecuación de Cauchy (Apéndice B) muestra que la distribución exponencial es la única distribución continua con esta propiedad.
Distribución gamma\((\alpha, \lambda)\)\(f_X(t) = \dfrac{\lambda^{\alpha} t^{\alpha - 1} e^{-\lambda t}}{\Gamma (\alpha)}\)\(t \ge 0\) (cero en otra parte)
Tenemos una función m-gammadbn para determinar los valores de la función de distribución para\(X~\) gamma\((\alpha, \lambda)\). El uso de funciones de generación de momentos muestra que para\(\alpha = n\), una variable aleatoria\(X~\) gamma\((n, \lambda)\) tiene la misma distribución que la suma de variables aleatorias\(n\) independientes, cada exponencial (\(lambda\)). Una relación con la distribución de Poisson se describe en la Sec 7.5.
Ejemplo\(\PageIndex{6}\): An arrival problem
En una noche de sábado, los horarios (en horas) entre las llegadas a una unidad de urgencias hospitalarias pueden estar representados por una cantidad aleatoria que es exponencial (\(\lambda = 3\)). Como mostramos en el capítulo Expectativa Matemática, esto significa que el tiempo promedio entre llegadas es de 1/3 hora o 20 minutos. ¿Cuál es la probabilidad de diez o más llegadas en cuatro horas? ¿En seis horas?
Solución
El tiempo para diez llegadas es la suma de diez tiempos entre llegadas. Si suponemos que estos son independientes, como suele ser el caso, entonces el tiempo para diez llegadas es gamma (10, 3).
>> p = gammadbn(10,3,[4 6]) p = 0.7576 0.9846
Normal, o\((\mu, \sigma^2)\)\(f_X (t) = \dfrac{1}{\sigma \sqrt{2 \pi}}\) exp\((-\dfrac{1}{2} (\dfrac{t - \mu}{\sigma})^2)\)\(\forall t\)
gaussiana Generalmente indicamos que una variable aleatoria\(X\) tiene la distribución normal o gaussiana escribiendo\(X ~ N(\mu, \sigma^2)\), poniendo en los valores reales para los parámetros. La distribución gaussiana juega un papel central en muchos aspectos de la teoría de probabilidad aplicada, particularmente en el área de la estadística. Gran parte de su importancia proviene del teorema del límite central (CLT), que es un término aplicado a una serie de teoremas en análisis. Esencialmente, el CLT muestra que la distribución para la suma de un número suficientemente grande de variables aleatorias independientes tiene aproximadamente la distribución gaussiana. Así, la distribución gaussiana aparece naturalmente en temas como la teoría de errores o la teoría del ruido, donde la cantidad observada es una combinación aditiva de un gran número de cantidades esencialmente independientes. El examen de la expresión muestra que la gráfica para\(f_X(t)\) es simétrica sobre su máximo en\(t = \mu\).. Cuanto mayor sea el parámetro\(\sigma^2\), menor será el valor máximo y más lentamente disminuye la curva con la distancia de\(\mu\).. Así\(\mu\) parámetros. localiza el centro de la distribución de masa y\(\sigma^2\) es una medida de la dispersión de la masa alrededor\(\mu\). El parámetro\(\mu\) se llama el valor medio y\(\sigma^2\) es la varianza. El parámetro\(\sigma\), la raíz cuadrada positiva de la varianza, se denomina desviación estándar. Si bien tenemos una fórmula explícita para la función de densidad, se sabe que la función de distribución, como la integral de la función de densidad, no puede expresarse en términos de funciones elementales. El procedimiento habitual es utilizar tablas obtenidas por integración numérica.
Dado que hay dos parámetros, esto plantea la cuestión de si se necesita una tabla separada para cada par de parámetros. Es un hecho notable que este no es el caso. Solo necesitamos tener una tabla de la función de distribución para\(X ~ N(0,1)\). Esto se conoce como la distribución normal estandarizada. Utilizamos\(\varphi\) y\(\phi\) para las funciones estandarizadas de densidad normal y distribución, respectivamente.
Normal estandarizada\(varphi(t) = \dfrac{1}{\sqrt{2 \pi}} e^{-t^2/2}\) para que la función de distribución sea\(\phi (t) = \int_{-\infty}^{t} \varphi (u) du\).
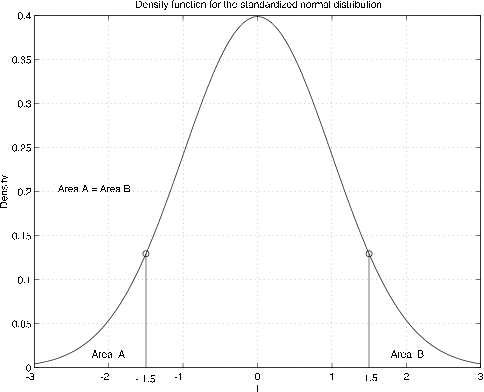
La gráfica de la función de densidad es la conocida curva en forma de campana, simétrica sobre el origen (ver Figura 7.1.4). La simetría sobre el origen contribuye a su utilidad.
Tenga en cuenta que el área a la izquierda de\(t = -1.5\) es la misma que la zona a la derecha de\(t = 1.5\), así que eso\(\phi (-2) = 1 - \phi(2)\). Lo mismo es cierto para cualquiera\(t\), para que tengamos
Esto indica que solo necesitamos una tabla de valores de\(\phi(t)\)\(t > 0\) para poder determinar\(\phi (t)\) para cualquiera\(t\). Podemos usar la simetría para cualquier caso. Tenga en cuenta que\(\phi(0) = 1/2\),
Ejemplo\(\PageIndex{7}\): Standardized normal calculations
Supongamos\(X ~ N(0, 1)\). Determinar\(P(-1 \le X \le 2)\) y\(P(|X| > 1)\)
Solución
- \(P(-1 \le X \le 2) = \phi (2) - \phi (-1) = \phi (2) - [1 - \phi(1)] = \phi (2) + \phi (1) - 1\)
- \(P(|X| > 1) = P(X > 1) + P(X < -1) = 1 - \phi(1) + \phi (-1) = 2[1 -\phi(1)]\)
De una tabla de función normalizada de distribución normal (ver Apéndice D), encontramos
\(\phi(2) = 0.9772\)y\(\phi(1) = 0.8413\) que da\(P(-1 \le X \le 2) = 0.8185\) y\(P(|X| > 1) = 0.3174\)
Distribución gaussiana general
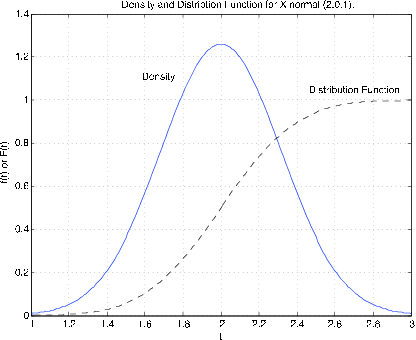
For\(X~N(\mu, \sigma^2)\), la densidad mantiene la forma de campana, pero se desplaza con diferente extensión y altura. La Figura 7.1.5 muestra la función de distribución y la función de densidad para\(X ~N(2, 0.1)\). La densidad se centra alrededor\(t = 2\). Tiene altura 1.2616 en comparación con 0.3989 para la densidad normal estandarizada. La inspección muestra que la gráfica es más estrecha que la de la normal estandarizada. La función de distribución alcanza 0.5 en el valor medio 2.
Un cambio de variables en la integral muestra que la tabla para la función de distribución normal estandarizada puede ser utilizada para cualquier caso.
Hacer el cambio de variable y cambios formales correspondientes
para obtener
\(F_X(t) = \int_{-\infty}^{(t-\mu)/\sigma} \varphi (u) du = \phi (\dfrac{t - \mu}{\sigma})\)
Ejemplo\(\PageIndex{8}\): General gaussian calculation
Supongamos\(X ~ N\) (3,16) (es decir,\(\mu = 3\) y\(\sigma^2 = 16\)). Determinar\(P(-1 \le X \le 11)\) y\(P(|X - 3| > 4)\).
Solución
- \(F_X(11) - F_X(-1) = \phi(\dfrac{11 - 3}{4}) - \phi(\dfrac{-1 - 3}{4}) = \phi(2) - \phi(-1) = 0.8185\)
- \(P(X - 3 < -4) + P(X - 3 >4) = F_X(-1) + [1 - F_X(7)] = \phi(-1) + 1 - \phi(1) = 0.3174\)
En cada caso el problema se reduce a eso en Ejemplo.
Contamos con funciones m gaussianas y gaussdensity para calcular los valores de la función de distribución y densidad para cualquier valor razonable de los parámetros.
Las siguientes son soluciones del ejemplo 7.1.7 y el ejemplo 7.1.8, usando la función m gaussiana.
Ejemplo\(\PageIndex{9}\): Example 7.1.7 and Example 7.1.8 (continued)
>> P1 = gaussian(0,1,2) - gaussian(0,1,-1) P1 = 0.8186 >> P2 = 2*(1 - gaussian(0,1,1)) P2 = 0.3173 >> P1 = gaussian(3,16,11) - gaussian(3,16,-1) P2 = 0.8186 >> P2 = gaussian(3,16,-1)) + 1 - (gaussian(3,16,7) P2 = 0.3173
Las diferencias en estos resultados y los anteriores (que utilizaron tablas) se deben al redondeo a cuatro lugares en las tablas.
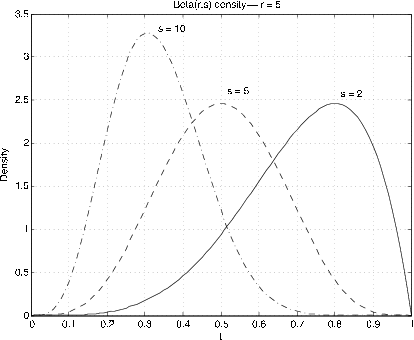
Beta\((r, s)\),\(r > 0\),\(s > 0\). \(f_X(t) = \dfrac{\Gamma(r + s)}{\Gamma(r) \Gamma(s)} t^{r - 1} (1 - t)^{s - 1}\)\(0 < t < 1\)
El análisis se basa en las integrales
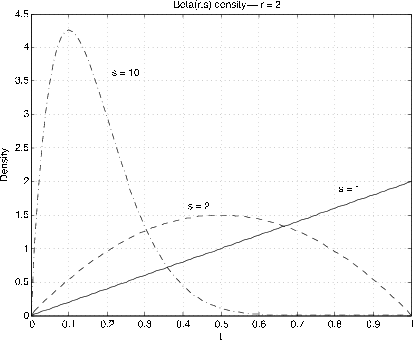
La Figura 7.6 y la Figura 7.7 muestran gráficas de las densidades para diversos valores de\(r, s\). La utilidad viene en aproximar densidades en el intervalo unitario. Mediante el uso de escalado y desplazamiento, estos se pueden extender a otros intervalos. El caso especial\(r = s = 1\) da la distribución uniforme en el intervalo de la unidad. La distribución Beta es bastante útil en el desarrollo de la estadística bayesiana para el problema del muestreo para determinar una proporción poblacional. Si\(r, s\) son enteros, la función de densidad es un polinomio. Para el caso general tenemos dos funciones m, beta y betadbn para realizar los cálculos.
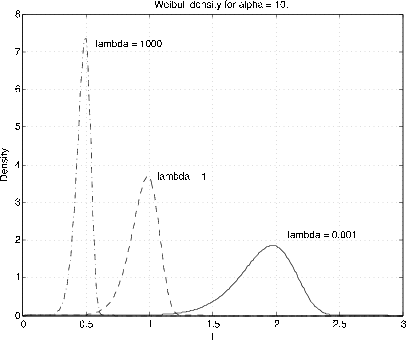
Weibull\((\alpha, \lambda, v)\)\(F_X (t) = 1 - e^{-\lambda (t - v)^{\alpha}}\)\(\alpha > 0\),\(\lambda > 0\),\(v \ge 0\),\(t \ge v\)
El parámetro\(v\) es un parámetro de desplazamiento. Por lo general asumimos\(v = 0\). El examen muestra que para α =1 la distribución es exponencial (\(\lambda\)). El parámetro α proporciona una distorsión de la escala de tiempo para la distribución exponencial. La Figura 7.6 y la Figura 7.7 muestran gráficas de la densidad de Weibull para algunos valores representativos de\(\alpha\) y\(\lambda\) (\(v = 0\)). La distribución se utiliza en la teoría de la confiabilidad. No hacemos mucho uso de ella. Sin embargo, tenemos las funciones m weibull (densidad) y weibulld (función de distribución) para el parámetro shift\(v = 0\) solamente. El desplazamiento se puede obtener restando una constante de los\(t\) valores.


