Una Variable Cuantitativa: Introducción
- Última actualización
- Guardar como PDF
- Page ID
- 151253
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)CO-4: Distinguir entre diferentes escalas de medición, elegir los métodos estadísticos descriptivos e inferenciales adecuados con base en estas distinciones e interpretar los resultados.
Video
Video: Una variable cuantitativa (4:16)
Nota
Tutoriales SAS relacionados
- 5A — (3:01) Medidas numéricas usando PROC MEANS
- 5B — (4:05) Creación de Histogramas y Gráficas de Caja usando SGPLOT
- 5C — (5:41) Crear gráficas QQ y otras gráficas usando UNIVARIATE
Tutoriales relacionados con SPSS
- 5A — (8:00) Medidas numéricas usando EXPLORE
- 5B — (2:29) Creación de histogramas y gráficas de caja
- 5C — (2:31) Creación de gráficas QQ y Pp-plots
Distribución de una variable cuantitativa
Objetivos de aprendizaje
LO 4.4: Usando pantallas gráficas y/o medidas numéricas apropiadas, describir la distribución de una variable cuantitativa en contexto: a) describir el patrón general, b) describir desviaciones llamativas del patrón
En la sección anterior, exploramos la distribución de una variable categórica utilizando gráficas (gráfico circular, gráfico de barras) complementadas con medidas numéricas (porcentaje de observaciones en cada categoría).
En esta sección, exploraremos los datos recopilados de una variable cuantitativa, y aprenderemos a describir y resumir las características importantes de su distribución.
Aprenderemos a mostrar la distribución usando gráficos y discutiremos una variedad de medidas numéricas.
A continuación se presenta una introducción a cada uno de estos temas.
Gráficas
Para mostrar gráficamente datos de una variable cuantitativa, podemos usar un histograma o una gráfica de caja.
También presentaremos varias pantallas “a mano” como el stemplot y dotplot (aunque no confiaremos en estos en este curso).
Medidas numéricas
El patrón general de distribución de una variable cuantitativa se describe por su forma, centro y extensión.
Al inspeccionar el histograma o diagrama de caja, podemos describir la forma de la distribución, pero solo podemos obtener una estimación aproximada para el centro y la propagación.
Una descripción de la distribución de una variable cuantitativa debe incluir, además de la visualización gráfica, una descripción numérica más precisa del centro y dispersión de la distribución.
En esta sección aprenderemos:
- cómo mostrar la distribución de una variable cuantitativa utilizando varias gráficas;
- cómo cuantificar el centro y la dispersión de la distribución de una variable cuantitativa con diversas medidas numéricas;
- algunas de las propiedades de esas medidas numéricas;
- cómo elegir las medidas numéricas apropiadas de centro y propagación para complementar la (s) gráfica (s); y
- cómo identificar posibles valores atípicos en la distribución de una variable cuantitativa
- También discutiremos algunas medidas de posición (también llamadas medidas de ubicación). Estas medidas
- nos permiten cuantificar donde un valor particular es relativo a la distribución de todos los valores
- proporcionar información sobre la distribución en sí
- también usa la información sobre la distribución para conocer más sobre un INDIVIDUAL
Presentaremos el material en una secuencia lógica que construye en dificultad, entremezclando la discusión de exhibiciones visuales y medidas numéricas a medida que avanzamos.
Antes de seguir leyendo, pruebe este applet interactivo que le dará una vista previa de algunos de los temas que aprenderemos en esta sección sobre análisis exploratorio de datos para una variable cuantitativa.
Applet interactivo: Analice una variable cuantitativa con esta calculadora estadística de una variable
Histogramas y Stemplots
CO-4: Distinguir entre diferentes escalas de medición, elegir los métodos estadísticos descriptivos e inferenciales adecuados con base en estas distinciones e interpretar los resultados.
Objetivos de aprendizaje
LO 4.4: Usando pantallas gráficas y/o medidas numéricas apropiadas, describir la distribución de una variable cuantitativa en contexto: a) describir el patrón general, b) describir desviaciones llamativas del patrón
Video
Video: Histogramas y Stemplots (5:03)
Nota
Tutoriales SAS relacionados
Tutoriales relacionados con SPSS
- 5B — (2:29) Creación de histogramas y gráficas de caja
Histogramas
Objetivos de aprendizaje
LO 4.5: Explicar el proceso de creación de un histograma.
La idea es romper el rango de valores en intervalos y contar cuántas observaciones caen en cada intervalo.
EJEMPLO: Grados
Aquí están los grados del examen de 15 alumnos:
88, 48, 60, 51, 57, 85, 69, 75, 97, 72, 71, 79, 65, 63, 73
Primero necesitamos romper el rango de valores en intervalos (también llamados “bins” o “clases”).
En este caso, dado que nuestro conjunto de datos consiste en puntuaciones de exámenes, tendrá sentido elegir intervalos que típicamente corresponden al rango de una calificación de letra, 10 puntos de ancho: [40,50), [50, 60),... [90, 100).
Al contar cuántas de las 15 observaciones caen en cada uno de los intervalos, obtenemos la siguiente tabla:
| Score | Contar |
|---|---|
| [40-50) | 1 |
| [50-60) | 2 |
| [60-70) | 4 |
| [70-80) | 5 |
| [80-90) | 2 |
| [90-100) | 1 |
Nota: La observación 60 se contó en el intervalo 60-70. Ver comentario 1 a continuación.
Para construir el histograma a partir de esta tabla trazamos los intervalos en el eje X, y mostramos el número de observaciones en cada intervalo (frecuencia del intervalo) en el eje Y, que se representa por la altura de un rectángulo ubicado por encima del intervalo:
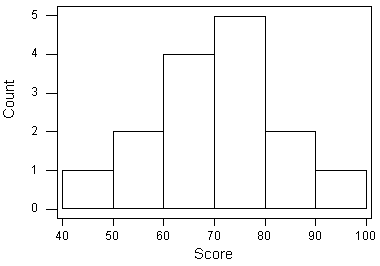
La tabla anterior también se puede convertir en una tabla de frecuencias relativas utilizando los siguientes pasos:
- Agregue una fila en la parte inferior e incluya el número total de observaciones en el conjunto de datos que se representan en la tabla.
- Agregue una columna, al final de la tabla, y calcule la frecuencia relativa para cada intervalo, dividiendo el número de observaciones en cada fila por el número total de observaciones.
Estos dos pasos se ilustran en rojo en la siguiente tabla de distribución de frecuencias:
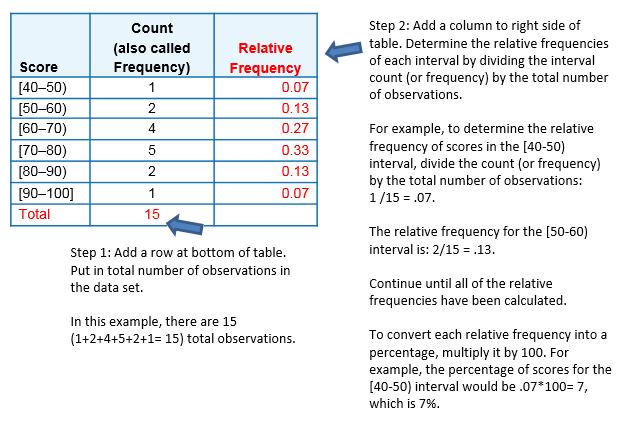
También es posible determinar el número de puntuaciones para un intervalo, si se tiene el número total de observaciones y la frecuencia relativa para ese intervalo.
- Por ejemplo, supongamos que hay 15 puntuaciones (u observaciones) en un conjunto de datos y la frecuencia relativa para un intervalo es de 0.13.
- Determinar el número de puntuaciones en ese intervalo, multiplicando el número total de observaciones por la frecuencia relativa y redondear hasta el siguiente número entero: 15*.13 = 1.95, que redondea hasta 2 observaciones.
Una tabla de frecuencias relativas, como la anterior, se puede utilizar para determinar la frecuencia de puntuaciones que ocurren a intervalos o a través de ellos.
Aquí hay algunos ejemplos, usando esta tabla de frecuencias:
¿Cuál es el porcentaje de puntajes de exámenes que fueron 70 y hasta, pero sin incluir, 80?
- Para determinar la respuesta, observamos la frecuencia relativa asociada con el intervalo [70-80).
- La frecuencia relativa es 0.33; para convertir a porcentaje, multiplicar por 100 (0.33*100= 33) o 33%.
¿Cuál es el porcentaje de puntajes de exámenes que son al menos 70? Para determinar la respuesta, necesitamos:
- Sumar las frecuencias relativas para los intervalos que tengan puntuaciones de al menos 70 o superiores.
- Así, sería necesario sumar las frecuencias relativas de [70-80), [80-90), y [90-100]
= 0.33 + 0.13 + 0.07 = 0.53. - Para obtener el porcentaje, es necesario multiplicar la frecuencia relativa calculada por 100.
- En este caso, sería 0.53*100 = 53 o 53%.
Estudie nuevamente el histograma y la tabla y responda a la siguiente pregunta.
Aprender haciendo: Histogramas
Comentarios:
- Es muy importante que cada observación se cuente sólo en un intervalo. En su mayor parte, está claro en qué intervalo cae una observación. Sin embargo, en nuestro ejemplo, necesitábamos decidir si incluir 60 en el intervalo 50-60, o el intervalo 60-70, y optamos por contarlo en este último.
- De hecho, esta decisión es captada por la forma en que escribimos los intervalos. Si te desplazas hacia arriba y miras la tabla, verás que escribimos los intervalos de una manera peculiar: [40-50), [50,60), [60,70) etc.
- El corchete significa “incluyendo” y el paréntesis significa “no incluir”. Por ejemplo, [50,60) es el intervalo de 50 a 60, incluyendo 50 y no incluyendo 60; [60,70) es el intervalo de 60 a 70, incluyendo 60, y no incluyendo 70, etc.
- Realmente no importa cómo decidas configurar tus intervalos, siempre y cuando seas consistente.
- Cuando miras un histograma como el anterior es importante saber que los valores que caen en el borde solo se cuentan en un intervalo, aunque no sepas de qué manera se hizo esto para una gráfica en particular.
- Cuando los datos se muestran en un histograma, se pierde cierta información. Tenga en cuenta que mirando el histograma
- podemos responder: “¿Cuántos alumnos obtuvieron 70 o más?” (5+2+1=8)
- Pero no podemos responder: “¿Cuál fue la puntuación más baja?” Todo lo que podemos decir es que la puntuación más baja está en algún lugar entre 40 y 50.
- Obviamente, podríamos haber optado por dividir los datos en intervalos de manera diferente —por ejemplo: [45, 50), [50, 55), [55, 60) etc.
Para ver cómo nuestra elección de bins o intervalos afecta a un histograma, puedes usar el applet vinculado a continuación que te permite cambiar los intervalos dinámicamente.
(OPCIONAL) Applet Interactivo: Histogramas
Muchos estudiantes se preguntan: Histogramas
Pregunta : ¿Cómo sé qué ancho de intervalo elegir?
Respuesta: Hay muchas opciones válidas para anchos de intervalo y puntos de partida. Existen algunas reglas generales utilizadas por los paquetes de software para encontrar valores óptimos. En este curso, nos basaremos en un paquete estadístico para producir el histograma por nosotros, y nos centraremos en su lugar en describir y resumir la distribución tal como aparece en el histograma.
Los siguientes ejercicios proporcionan más práctica trabajando con histogramas creados a partir de una única variable cuantitativa.
¿Recibí esto? : Histogramas
Estemplot (Trama de tallo y hoja)
Objetivos de aprendizaje
LO 4.6: Explicar el proceso de creación de un stemplot.
El estemplot (también llamado diagrama de tallo y hoja) es otra representación gráfica de la distribución de la variable cuantitativa.
Nota
Para crear un stemplot, la idea es separar cada punto de datos en un tallo y una hoja, de la siguiente manera:
- La hoja es el dígito más a la derecha.
- El tallo lo es todo excepto el dígito más a la derecha.
- Entonces, si el punto de datos es 34, entonces 3 es el tallo y 4 es la hoja.
- Si el punto de datos es 3.41, entonces 3.4 es el tallo y 1 es la hoja.
- Nota: Para que esto funcione, TODOS los puntos de datos deben redondearse al mismo número de decimales.
EJEMPLO: Mejor Actriz Ganadora
Continuaremos con el ejemplo de ganadores del Oscar a Mejor Actriz (Enlace a los datos de los ganadores del Oscar a la Mejor Actriz).
34 34 26 37 42 41 35 31 41 33 30 74 33 49 38 61 21 41 26 80 43 29 33 35 45 49 39 34 26 25 35 33
Para hacer un stemplot:
- Separar cada observación en un tallo y una hoja.
- Escribe los tallos en una columna vertical con el más pequeño en la parte superior, y dibuja una línea vertical a la derecha de esta columna.
- Ir a través de los puntos de datos, y escribir cada hoja en la fila a la derecha de su tallo.
- Reorganizar las hojas en un orden creciente.

* Cuando algunos de los tallos sostienen una gran cantidad de hojas, podemos dividir cada tallo en dos: uno sosteniendo las hojas 0-4, y el otro sosteniendo las hojas 5-9. Un paquete de software estadístico a menudo hará la división por usted, cuando sea apropiado.
Tenga en cuenta que cuando se gira 90 grados en sentido antihorario, el stemplot se parece visualmente a un histograma:
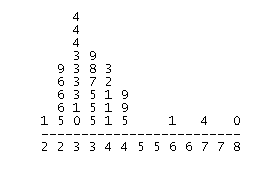
El stemplot tiene características únicas adicionales:
- Conserva los datos originales.
- Ordena los datos (que serán muy útiles en la siguiente sección).
No necesitarás crear estas parcelas a mano pero quizás necesites poder discutir la información que contienen.
Para ver más stemplots, usa el applet interactivo que presentamos anteriormente.
En particular, observe cómo se redondean los datos brutos y observe el stemplot con y sin tallos divididos.
Applet interactivo: Analice una variable cuantitativa con esta calculadora estadística de una variable
Comentarios: SOBRE DOTPLOTS
- Hay otro tipo de visualización que podemos usar para resumir gráficamente una variable cuantitativa: la gráfica de puntos.
- La gráfica de puntos, al igual que el stemplot, muestra cada observación, pero la muestra con un punto en lugar de con su valor real.
- No los usaremos en este curso pero es posible que los veas ocasionalmente en la práctica y son relativamente fáciles de crear a mano.
- Aquí está la trama de puntos para las edades de los ganadores del Oscar a Mejor Actriz.
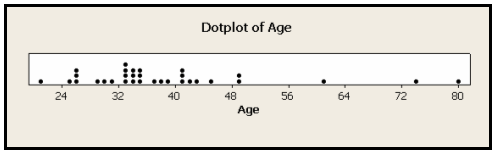
Muchos estudiantes se preguntan: Gráficas
Pregunta: ¿Cómo sabemos qué gráfico usar: el histograma, stemplot o dotplot?
Respuesta Dado que en su mayor parte no vamos a tratar con conjuntos de datos muy pequeños en este curso, generalmente mostraremos la distribución de una variable cuantitativa utilizando un histograma generado por un paquete de software estadístico.
Resumimos
- El histograma es una visualización gráfica de la distribución de una variable cuantitativa. Se traza el número (conteo) de observaciones que caen en intervalos de valores.
- El stemplot es una simple pero útil visualización de una variable cuantitativa. Sus principales virtudes son:
- Fácil y rápido de construir para conjuntos de datos pequeños y simples.
- Conserva los datos reales.
- Ordena (clasifica) los datos.
Describiendo las distribuciones
CO-4: Distinguir entre diferentes escalas de medición, elegir los métodos estadísticos descriptivos e inferenciales adecuados con base en estas distinciones e interpretar los resultados.
Objetivos de aprendizaje
LO 4.4: Usando pantallas gráficas y/o medidas numéricas apropiadas, describir la distribución de una variable cuantitativa en contexto: a) describir el patrón general, b) describir desviaciones llamativas del patrón
Video
Video: Describiendo distribuciones (2 videos, 7:38 total)
Nota
Tutoriales SAS relacionados
- 5A — (3:01) Medidas numéricas usando PROC MEANS
- 5B — (4:05) Creación de Histogramas y Gráficas de Caja usando SGPLOT
- 5C — (5:41) Crear gráficas QQ y otras gráficas usando UNIVARIATE
Tutoriales relacionados con SPSS
- 5A — (8:00) Medidas numéricas usando EXPLORE
- 5B — (2:29) Creación de histogramas y gráficas de caja
- 5C — (2:31) Creación de gráficas QQ y Pp-plots
Características de Distribuciones de Variables Cuantitativas
Objetivos de aprendizaje
LO 4.7: Definir y describir las características de la distribución de una variable cuantitativa (forma, centro, propagación, valores atípicos).
Una vez que la distribución se ha mostrado gráficamente, podemos describir el patrón general de la distribución y mencionar cualquier desviación llamativa de ese patrón.
Nota
Más específicamente, debemos considerar las siguientes características de la Distribución para una Variable Cuantitativa:

Forma
Al describir la forma de una distribución, debemos considerar:
- Simmetría/asimetría de la distribución.
- Peakedness (modalidad) — el número de picos (modos) que tiene la distribución.
Distinguimos entre:
Distribuciones simétricas
Nota
Una distribución se denomina simétrica si, como en los histogramas anteriores, la distribución forma una imagen especular aproximada con respecto al centro de la distribución.
El centro de la distribución es fácil de localizar y ambas colas de la distribución son aproximadamente de la misma longitud.
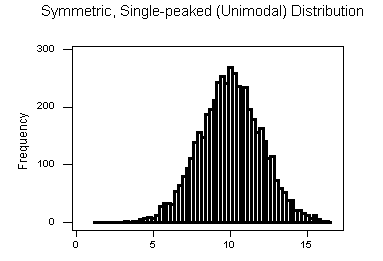
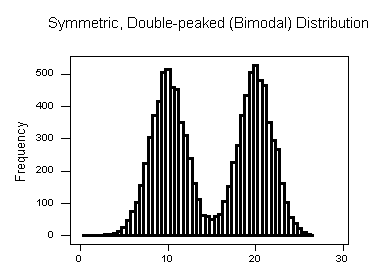
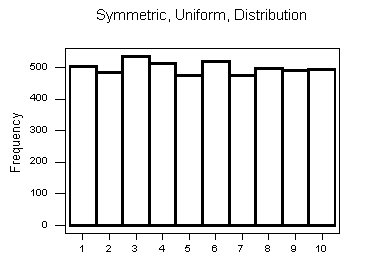
Tenga en cuenta que las tres distribuciones son simétricas, pero son diferentes en su modalidad (pico).
- La primera distribución es unimodal — tiene un modo (aproximadamente a 10) alrededor del cual se concentran las observaciones.
- La segunda distribución es bimodal —tiene dos modos (aproximadamente a 10 y 20) alrededor de los cuales se concentran las observaciones.
- La tercera distribución es una especie de plano, o uniforme. La distribución no tiene modos, o ningún valor alrededor del cual se concentran las observaciones. Más bien, vemos que las observaciones se distribuyen aproximadamente de manera uniforme entre los diferentes valores.
Distribuciones a la derecha sesgada
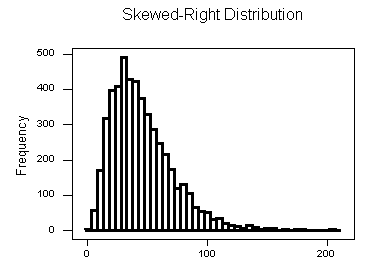
Una distribución se llama sesgada a la derecha si, como en el histograma anterior, la cola derecha (valores mayores) es mucho más larga que la cola izquierda (valores pequeños).
Obsérvese que en una distribución derecha sesgada, la mayor parte de las observaciones son pequeñas/medianas, con algunas observaciones que son mucho mayores que el resto.
- Un ejemplo de una variable de la vida real que tiene una distribución derecha sesgada es el salario. La mayoría de las personas ganan en el rango bajo/medio de salarios, con algunas excepciones (CEOs, atletas profesionales etc.) que se distribuyen a lo largo de un amplio rango (larga “cola”) de valores más altos.
Distribuciones sesgadas a la izquierda
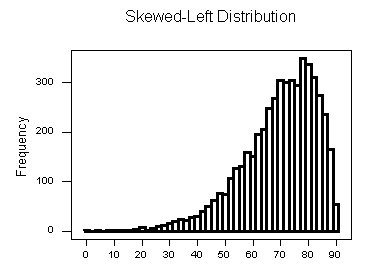
Una distribución se llama sesgada a la izquierda si, como en el histograma anterior, la cola izquierda (valores más pequeños) es mucho más larga que la cola derecha (valores más grandes).
Obsérvese que en una distribución sesgada a la izquierda, la mayor parte de las observaciones son medias/grandes, con algunas observaciones que son mucho más pequeñas que el resto.
- Un ejemplo de una variable de la vida real que tiene una distribución sesgada a la izquierda es la edad de muerte por causas naturales (enfermedades cardíacas, cáncer etc.). La mayoría de esas muertes ocurren a edades más avanzadas, con menos casos que ocurren a edades más tempranas.
Comentarios:
- Las distribuciones con más de dos picos generalmente se denominan multimodales.
- Las distribuciones bimodales o multimodales pueden ser evidencia de que se representan dos grupos distintos.
- Las distribuciones unimodales, bimodales y multimodales pueden ser o no simétricas.
Aquí hay un ejemplo. Una tienda de conveniencia de tamaño mediano de 24 horas del vecindario recopiló datos de 537 clientes sobre la cantidad de dinero gastado en una sola visita a la tienda. El siguiente histograma muestra los datos.
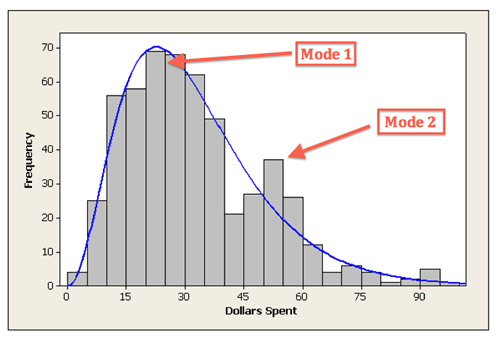
Tenga en cuenta que la forma general de la distribución está sesgada hacia la derecha con un modo claro alrededor de $25. Además, tiene otro “pico” (modo) (más pequeño) alrededor de 50-55 dólares.
La mayoría de los clientes gastan alrededor de 25 dólares pero hay un grupo de clientes que ingresan a la tienda y gastan alrededor de $50-55.
Centro
El centro de la distribución suele utilizarse para representar un valor típico.
Una forma de definir el centro es como el valor que divide la distribución de manera que aproximadamente la mitad de las observaciones toman valores más pequeños, y aproximadamente la mitad de las observaciones toman valores mayores.
Otra forma común de medir el centro de una distribución es utilizar el valor promedio.
Al mirar el histograma solo podemos obtener una estimación aproximada para el centro de la distribución. En la siguiente sección se discutirán formas más exactas de encontrar medidas de centro.
Spread
Una forma de medir la propagación (también llamada variabilidad o variación) de la distribución es utilizar el rango aproximado cubierto por los datos.
Al mirar el histograma, podemos aproximar la observación más pequeña (min), y la observación más grande (máx), y así aproximar el rango. (Pronto se discutirán formas más exactas de encontrar medidas de propagación).
valores atípicos
Los valores atípicos son observaciones que caen fuera del patrón general.
Por ejemplo, el siguiente histograma representa una distribución con un valor atípico altamente probable:
10 tienen una frecuencia de 0, excepción para x=15, que tiene una frecuencia mayor a cero. Esto es un valor atípico.” height="258" loading="lazy” src=” http://phhp-faculty-cantrell.sites.m...histogram7.gif "title="Un histograma con frecuencia en el eje Y. A medida que avanzamos de izquierda a derecha en el eje x, la frecuencia aumenta a un pico en x=5, luego disminuye. Eventualmente, alcanzamos 0 en x=11. Todos x > 10 tienen una frecuencia de 0, a excepción de x=15, que tiene una frecuencia mayor a cero. Esto es un valor atípico.” width="377">
EJEMPLO: Grados
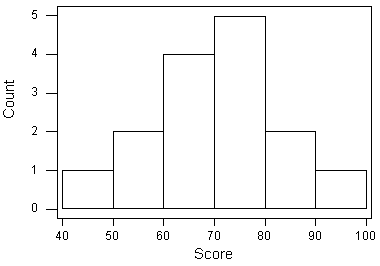
Como puede ver en el histograma, la distribución de calificaciones es aproximadamente simétrica y unimodal sin valores atípicos.
El centro de la distribución de calificaciones es aproximadamente 70 (7 estudiantes obtuvieron calificaciones por debajo de 70, y 8 estudiantes obtuvieron calificaciones superiores a 70).
| min aproximado: | 45 (la mitad del intervalo más bajo de puntuaciones) |
| max aproximado: | 95 (la mitad del intervalo más alto de puntajes) |
| rango aproximado: | 95-45=50 |
Veamos un nuevo ejemplo.
EJEMPLO: Mejor Actriz Ganadora
Para dar un ejemplo de un histograma aplicado a datos reales, veremos las edades de los ganadores del Oscar a la Mejor Actriz de 1970 a 2001
A continuación se muestra el histograma de los datos. (Enlace a los datos de los ganadores del Oscar a la Mejor Actriz).
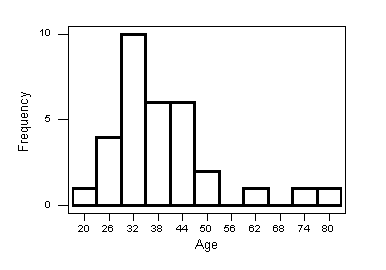
A continuación resumiremos las principales características de la distribución de edades tal como aparece en el histograma:
Forma: La distribución de edades está sesgada a la derecha. Tenemos una concentración de datos entre las edades más jóvenes y una larga cola a la derecha. La gran mayoría de los premios a la “mejor actriz” se entregan a actrices jóvenes, con muy pocos premios otorgados a actrices mayores.
Centro: Los datos parecen estar centrados alrededor de 35 o 36 años de edad. Tenga en cuenta que esto implica que aproximadamente la mitad de los premios se entregan a actrices que tienen menos de 35 años de edad.
Spread: Los datos van desde aproximadamente 20 hasta aproximadamente 80, por lo que el rango aproximado es igual a 80 — 20 = 60.
Valores atípicos: Parece que hay dos probables valores atípicos a la extrema derecha y posiblemente un tercero alrededor de los 62 años de edad.
Se puede ver lo informativo que es saber “qué mirar” en un histograma.
Aprende haciendo: Formas de distribuciones (Ganadores del Oscar al mejor actor)
Los siguientes ejercicios proporcionan más práctica con formas de distribuciones para una variable cuantitativa.
¿Recibí esto? : Formas de Distribuciones
¿Recibí esto? : Formas de Distribuciones Parte 2
Resumimos
- Al examinar la distribución de una variable cuantitativa, se debe describir el patrón general de los datos (forma, centro, dispersión), y cualquier desviación del patrón (valores atípicos).
- Al describir la forma de una distribución, se debe considerar:
- Simmetría/asimetría de la distribución
- Peakedness (modalidad) — el número de picos (modos) que tiene la distribución.
- No todas las distribuciones tienen una forma simple y reconocible.
- Los valores atípicos son puntos de datos que quedan fuera del patrón general de la distribución y necesitan más investigación antes de continuar con el análisis.
- Siempre es importante interpretar lo que significan las características de la distribución en el contexto de los datos.
Medidas de Centro
CO-4: Distinguir entre diferentes escalas de medición, elegir los métodos estadísticos descriptivos e inferenciales adecuados con base en estas distinciones e interpretar los resultados.
Objetivos de aprendizaje
LO 4.4: Usando pantallas gráficas y/o medidas numéricas apropiadas, describir la distribución de una variable cuantitativa en contexto: a) describir el patrón general, b) describir desviaciones llamativas del patrón
Objetivos de aprendizaje
LO 4.7: Definir y describir las características de la distribución de una variable cuantitativa (forma, centro, propagación, valores atípicos).
Video
Video: Medidas del Centro (2 videos, 6:09 total)
Nota
Tutoriales SAS relacionados
- 5A — (3:01) Medidas numéricas usando PROC MEANS
Tutoriales relacionados con SPSS
- 5A — (8:00) Medidas numéricas usando EXPLORE
Introducción
Intuitivamente hablando, una medida numérica del centro describe un “valor típico” de la distribución.
Las dos medidas numéricas principales para el centro de una distribución son la media y la mediana.
En esta unidad de Análisis Exploratorio de Datos, estaremos calculando estos resultados con base en una muestra y por lo que a menudo enfatizaremos que los valores calculados son la media de la muestra y la mediana de la muestra.
Cada una de estas medidas se basa en una idea completamente diferente de describir el centro de una distribución.
Primero presentaremos cada una de las medidas, y luego compararemos sus propiedades.
Media
Objetivos de aprendizaje
LO 4.8: Definir y calcular la media muestral de una variable cuantitativa.
Ejemplo
La media es la media de un conjunto de observaciones (es decir, la suma de las observaciones dividida por el número de observaciones).
La media es el promedio de un conjunto de observaciones
- La suma de las observaciones dividida por el número de observaciones).
- Si las n observaciones se escriben como
\(x_1, x_2, \cdots, x_n\)
- su media puede escribirse matemáticamente como:su media es:
\(\bar{x}=\dfrac{x_{1}+x_{2}+\cdots+x_{n}}{n}=\dfrac{\sum_{i=1}^{n} x_{i}}{n}\)
Leemos el símbolo como “barra x”. La notación de barras se usa comúnmente para representar la media de la muestra, es decir, la media de la muestra.
Usando cualquier letra apropiada para representar la variable (x, y, etc.), podemos indicar la media muestral de esta variable añadiendo una barra sobre la notación variable.
EJEMPLO: Mejor Actriz Ganadora
Continuaremos con el ejemplo de ganadores del Oscar a Mejor Actriz (Enlace a los datos de los ganadores del Oscar a la Mejor Actriz).
34 34 26 37 42 41 35 31 41 33 30 74 33 49 38 61 21 41 26 80 43 29 33 35 45 49 39 34 26 25 35 33
La edad media de las 32 actrices es:
\(\bar{x}=\dfrac{34+34+26+\ldots+35+33}{32}=\dfrac{1233}{32}=38.5\)
Agregamos todas las edades para obtener 1233 y dividimos por el número de edades que era 32 para obtener 38.5.
Denotamos este resultado como barra x y llamamos la media de la muestra.
Obsérvese que la media de la muestra da una medida del centro que es mayor que nuestra aproximación del centro al observar el histograma (que fue 35). El motivo de esto quedará claro pronto.
EJEMPLO: Copa Mundial de Futbol
A menudo tenemos grandes conjuntos de datos y utilizamos una tabla de frecuencias para mostrar los datos de manera más eficiente.
Se recolectaron datos de los tres últimos torneos de fútbol de la Copa Mundial. Se disputaron un total de 192 juegos. La siguiente tabla enumera el número de goles marcados por partido (sin incluir ningún gol anotado en tiroteos).
| Total # Goles/Juego | Frecuencia |
|---|---|
| 0 | 17 |
| 1 | 45 |
| 2 | 51 |
| 3 | 37 |
| 4 | 25 |
| 5 | 11 |
| 6 | 3 |
| 7 | 2 |
| 8 | 1 |
Para encontrar el número medio de goles marcados por partido, necesitaríamos encontrar la suma de los 192 números, y luego dividir esa suma entre 192.
En lugar de sumar 192 números, utilizamos el hecho de que los mismos números aparecen muchas veces. Por ejemplo, el número 0 aparece 17 veces, el número 1 aparece 45 veces, el número 2 aparece 51 veces, etc.
Si sumamos 17 ceros, obtenemos 0. Si sumamos 45 unos, obtenemos 45. Si sumamos 51 dos, obtenemos 102. La adición repetida es la multiplicación.
Así, la suma de los 192 números
= 0 (17) + 1 (45) + 2 (51) + 3 (37) + 4 (25) + 5 (11) + 6 (3) + 7 (2) + 8 (1) = 453.
La media muestral es entonces 453/192 = 2.359.
Tenga en cuenta que, en este ejemplo, los valores de 1, 2 y 3 son los más comunes y nuestro promedio cae en este rango representando la mayor parte de los datos.
¿Recibí esto? : Media
Mediana
Objetivos de aprendizaje
LO 4.9: Definir y calcular la mediana muestral de una variable cuantitativa.
La mediana M es el punto medio de la distribución. Es el número tal que la mitad de las observaciones caen por encima, y la mitad caen por debajo.
Para encontrar la mediana:
- Ordene los datos de menor a mayor.
- Considera si n, el número de observaciones, es par o impar.
- Si n es impar, la mediana M es la observación central en la lista ordenada. Esta observación es la que está “sentada” en el lugar (n + 1)/2 en la lista ordenada.
- Si n es par, la mediana M es la media de las dos observaciones centrales en la lista ordenada. Estas dos observaciones son las “sentadas” en el (n/2) y (n/2) + 1 manchas en la lista ordenada.
EJEMPLO: Mediana (1)
Para una simple visualización de la ubicación de la mediana, considere los siguientes dos casos simples de n = 7 y n = 8 observaciones ordenadas, con cada observación representada por un círculo sólido:
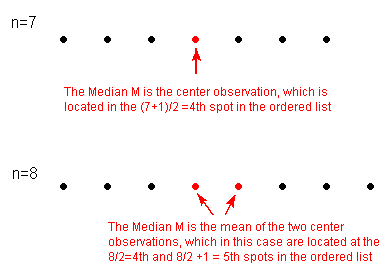
Comentarios:
- En las imágenes anteriores, los puntos están igualmente espaciados, esto no necesita indicar que los valores de datos en realidad están igualmente espaciados ya que solo nos interesa enumerarlos en orden.
- De hecho, en las imágenes anteriores, dos puntos posteriores podrían tener exactamente el mismo valor.
- Es claro que el valor de la mediana estará en la misma posición independientemente de la distancia entre los valores de datos.
¿Recibí esto? : Mediana
EJEMPLO: Mediana (2)
Para encontrar la mediana de edad de los ganadores del Oscar a la Mejor Actriz, primero necesitamos ordenar los datos.
Sería útil, entonces, utilizar el stemplot, un diagrama en el que ya están ordenados los datos.
- Aquí n = 32 (un número par), por lo que la mediana M, será la media de las dos observaciones centrales
- Estos se ubican en el (n/2) = 32/2 = 16 y (n/2) + 1 = (32/2) + 1 = 17
Contando desde arriba, encontramos que:
- la observación en el puesto 16 es 35
- la observación clasificada 17 también pasa a ser 35
Por lo tanto, la mediana M = (35 + 35)/2 = 35

Aprende haciendo: Medidas de Centro #1
Comparando la Media y la Mediana
Objetivos de aprendizaje
LO 4.10: Elegir las medidas adecuadas para una variable cuantitativa con base en la forma de la distribución.
Nota
Como hemos visto, la media y la mediana, las medidas más comunes de centro, cada una describe el centro de una distribución de valores de una manera diferente.
- La media describe al centro como un valor promedio, en el que los valores reales de los puntos de datos juegan un papel importante.
- La mediana, por otro lado, localiza el valor medio como el centro, y el orden de los datos es la clave.
Para obtener una comprensión más profunda de las diferencias entre estas dos medidas de centro, considere el siguiente ejemplo. Aquí hay dos conjuntos de datos:
| Conjunto de datos A → 64 65 66 68 70 71 73 |
| Conjunto de datos B → 64 65 66 68 70 71 730 |
Para el conjunto de datos A, la media es 68.1 y la mediana es 68.
Al observar el conjunto de datos B, observe que todas las observaciones excepto la última están muy juntas. La observación 730 es muy grande, y sin duda es un valor atípico.
En este caso, la mediana sigue siendo de 68, pero la media estará influenciada por el valor atípico alto, y se desplazó hasta 162.
El mensaje que debemos tomar de este ejemplo es:
La media es muy sensible a los valores atípicos (porque tiene en cuenta su magnitud), mientras que la mediana es resistente (o robusta) a los valores atípicos.
Applet interactivo: Comparación de la media y la mediana
Por lo tanto:
- Para distribuciones simétricas sin valores atípicos: la media es aproximadamente igual a la mediana.
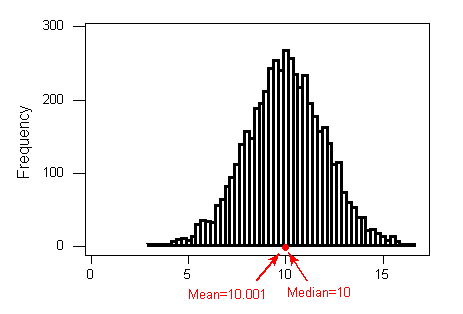
- Para distribuciones derechas sesgadas y/o conjuntos de datos con valores atípicos altos: la media es mayor que la mediana.
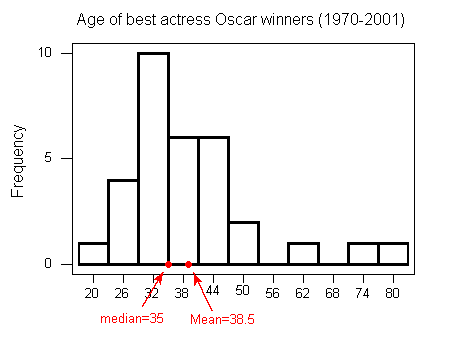
- Para distribuciones izquierdas sesgadas y/o datasets con valores atípicos bajos: la media es menor que la mediana.
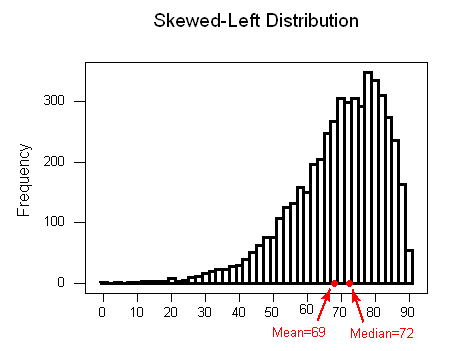
Conclusiones... ¿Cuándo usar qué medidas?
- Utilizar la media muestral como medida del centro para distribuciones simétricas sin valores atípicos.
- De lo contrario, la mediana será una medida más apropiada del centro de nuestros datos.
¿Recibí esto? : Medidas de Centro
Aprende haciendo: Medidas de Centro #2
Aprender haciendo: Medidas de Centro — Práctica Adicional
Resumimos
- Las dos medidas numéricas principales para el centro de una distribución son la media y la mediana. La media es el valor promedio, mientras que la mediana es el valor medio.
- La media es muy sensible a los valores atípicos (ya que tiene en cuenta su magnitud), mientras que la mediana es resistente a los valores atípicos.
- La media es una medida apropiada del centro para distribuciones simétricas sin valores atípicos. En todos los demás casos, la mediana suele ser una mejor medida del centro de la distribución.
Medidas de propagación
CO-4: Distinguir entre diferentes escalas de medición, elegir los métodos estadísticos descriptivos e inferenciales adecuados con base en estas distinciones e interpretar los resultados.
Objetivos de aprendizaje
LO 4.4: Usando pantallas gráficas y/o medidas numéricas apropiadas, describir la distribución de una variable cuantitativa en contexto: a) describir el patrón general, b) describir desviaciones llamativas del patrón
Objetivos de aprendizaje
LO 4.7: Definir y describir las características de la distribución de una variable cuantitativa (forma, centro, propagación, valores atípicos).
Video
Video: Medidas de propagación (3 videos, 8:44 total)
Nota
Tutoriales SAS relacionados
- 5A — (3:01) Medidas numéricas usando PROC MEANS
Tutoriales relacionados con SPSS
- 5A — (8:00) Medidas numéricas usando EXPLORE
Introducción
Hasta el momento hemos aprendido diferentes formas de cuantificar el centro de una distribución. Sin embargo, una medida de centro por sí misma no es suficiente para describir una distribución.
Considera las siguientes dos distribuciones de puntajes de exámenes. Ambas distribuciones están centradas en 70 (la mediana de ambas distribuciones es aproximadamente 70), pero las distribuciones son bastante diferentes.
La primera distribución tiene una variabilidad mucho mayor en las puntuaciones en comparación con la segunda.
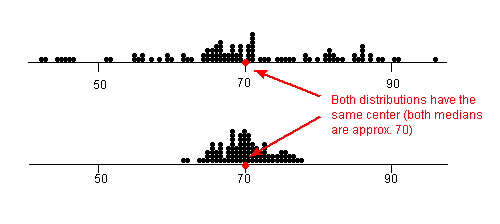
Para describir la distribución, por lo tanto, necesitamos complementar la visualización gráfica no solo con una medida de centro, sino también con una medida de la variabilidad (o propagación) de la distribución.
En esta sección, discutiremos las tres medidas de propagación más utilizadas:
- Rango
- Inter-cuartil rango (IQR)
- Desviación estándar
Si bien las medidas de centro sí abordaron la cuestión de manera diferente, sí intentan medir el mismo punto en la distribución y así son comparables.
Sin embargo, las tres medidas de propagación proporcionan formas muy diferentes de cuantificar la variabilidad de la distribución y no intentan estimar la misma cantidad.
De hecho, las tres medidas de difusión proporcionan información sobre tres aspectos diferentes de la difusión de la distribución que, en conjunto, dan una imagen más completa de la difusión de la distribución.
Rango
Objetivos de aprendizaje
LO 4.11: Definir y calcular el rango de una variable cuantitativa.
El rango cubierto por los datos es la medida de variabilidad más intuitiva. El rango es exactamente la distancia entre el punto de datos más pequeño (min) y el más grande (Max).
- Rango = Máx — min
Nota: Cuando miramos por primera vez el histograma, e intentamos tener una primera idea de la propagación de los datos, en realidad estábamos aproximando el rango, en lugar de calcular el rango exacto.
EJEMPLO: Mejor Actriz Ganadora
Aquí tenemos los datos de los ganadores del Oscar a la Mejor Actriz
34 34 26 37 42 41 35 31 41 33 30 74 33 49 38 61 21 41 26 80 43 29 33 35 45 49 39 34 26 25 35 33
En este ejemplo:
- min = 21 (Marlee Matlin para hijos de un dios menor, 1986)
- Max = 80 (Jessica Tandy para Driving Miss Daisy, 1989)
El rango que abarca todos los datos es de 80 — 21 = 59 años.
Rango Inter-Cuartil (IQR)
Objetivos de aprendizaje
LO 4.12: Definir y calcular Q1, Q3 y el IQR para una variable cuantitativa
Mientras que el rango cuantifica la variabilidad observando el rango cubierto por TODOS los datos,
el Rango Inter-Cuartil o IQR mide la variabilidad de una distribución dándonos el rango cubierto por el MEDIO 50% de los datos.
- IQR = Q3 — Q1
- Q3 = 3 rd Cuartil = percentil 75 th
- Q1 = 1 st Cuartil = percentil 25 th
La siguiente imagen ilustra esta idea: (Piense en la línea horizontal como los datos que van desde el mínimo hasta el máximo). NOTA IMPORTANTE: Las “líneas” en las siguientes ilustraciones no están a escala. Las distancias iguales indican cantidades iguales de datos NO igual distancia entre los valores numéricos.
Aunque utilizaremos software para calcular los cuartiles y el IQR, ilustraremos el proceso básico para ayudarte a comprender completamente.
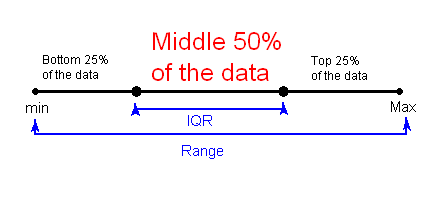
Para calcular el IQR:
- Organizar los datos en orden creciente, y encontrar la mediana M. Recordemos que la mediana divide los datos, de manera que 50% de los puntos de datos están por debajo de la mediana, y 50% de los puntos de datos están por encima de la mediana.
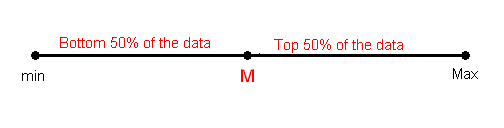
2. Encuentra la mediana del 50% inferior de los datos. Esto se llama el primer cuartil de la distribución, y el punto se denota con Q1. Observe de la imagen que Q1 divide el 50% inferior de los datos en dos mitades, conteniendo 25% de los puntos de datos en cada mitad. Q1 se llama el primer cuartil, ya que una cuarta parte de los puntos de datos caen por debajo de él.
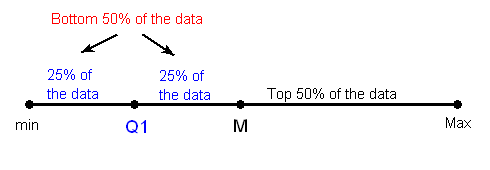
3. Repita esto nuevamente para el 50% superior de los datos. Encuentra la mediana del 50% superior de los datos. Este punto se llama el tercer cuartil de la distribución, y se denota por Q3.
Observe de la imagen que Q3 divide el 50% superior de los datos en dos mitades, con 25% de los puntos de datos en cada.Q3 se denomina tercer cuartil, ya que tres cuartas partes de los puntos de datos caen por debajo de él.
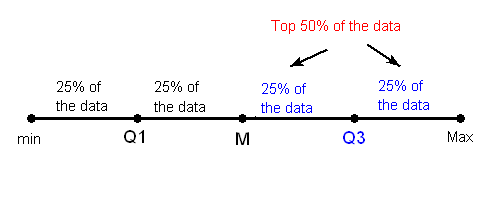
4. El 50% medio de los datos cae entre Q1 y Q3, y por lo tanto: IQR = Q3 — Q1
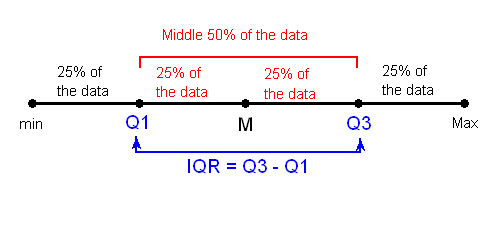
Comentarios:
- La última imagen muestra que Q1, M y Q3 dividen los datos en cuatro cuartos con 25% de los puntos de datos en cada uno, donde la mediana es esencialmente el segundo cuartil. Por lo tanto, el uso de IQR = Q3 — Q1 como medida de propagación es particularmente apropiado cuando se usa la mediana M como medida del centro.
- Podemos definir un poco más precisamente lo que se considera el 50% inferior o superior de los datos. El 50% inferior (superior) de los datos son todas las observaciones cuya posición en la lista ordenada está a la izquierda (derecha) de la ubicación de la mediana general M. La siguiente imagen ilustrará visualmente esto para los casos simples de n = 7 y n = 8.
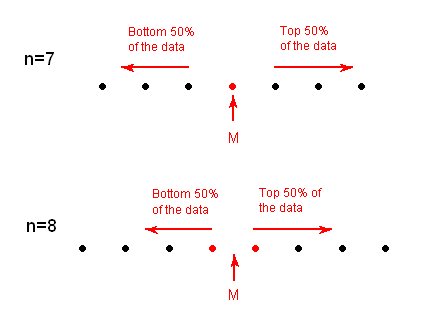
Tenga en cuenta que cuando n es impar (como en n = 7 anterior), la mediana no se incluye ni en la mitad inferior ni en la parte superior de los datos; Cuando n es par (como en n = 8 anterior), los datos se dividen naturalmente en dos mitades.
EJEMPLO: Mejor Actriz Ganadora
Para encontrar el IQR de la distribución de los ganadores del Oscar a la Mejor Actriz, será conveniente usar el stemplot.

Q1 es la mediana de la mitad inferior de los datos. Dado que hay 16 observaciones en esa mitad, Q1 es la media de las observaciones 8 y 9 clasificadas en esa mitad:
Q1 = (31 + 33)/2 = 32
De igual manera, Q3 es la mediana de la mitad superior de los datos, y dado que hay 16 observaciones en esa mitad, Q3 es la media de las observaciones clasificadas 8 y 9 en esa mitad:
Q3 = (41 + 42)/2 = 41.5
IQR = 41.5 — 32 = 9.5
Obsérvese que en este ejemplo, el rango que abarca todas las edades es de 59 años, mientras que el rango que abarca el 50% medio de las edades es de sólo 9.5 años. Si bien todo el conjunto de datos está distribuido en un rango de 59 años, el 50% medio de los datos se empaqueta en solo 9.5 años. Mirando de nuevo el histograma ilustrará esto:
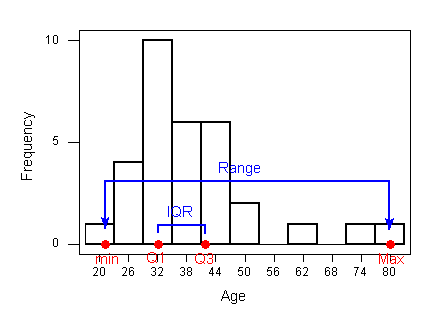
Comentario:
- Los paquetes de software utilizan diferentes fórmulas para calcular los cuartiles Q1 y Q3. Esto no te debe preocupar, siempre y cuando entiendas la idea detrás de estos conceptos. Por ejemplo, aquí están los valores cuartiles proporcionados por tres paquetes de software diferentes para la era de los ganadores del Oscar a la mejor actriz:
R:
![]()
Minitab:

Excel:
![]()
Q1 y Q3 según lo informado por los diversos paquetes de software difieren entre sí y también son ligeramente diferentes de los que encontramos aquí. Esto no te debe preocupar.
Existen diferentes formas aceptables de encontrar la mediana y los cuartiles. Estos pueden dar resultados diferentes ocasionalmente, especialmente para conjuntos de datos donde n (el número de observaciones) es bastante pequeño.
Siempre y cuando sepas lo que significan los números, y cómo interpretarlos en contexto, realmente no importa mucho qué método uses para encontrarlos, ya que las diferencias son despreciables.
Desviación estándar
Objetivos de aprendizaje
LO 4.13: Definir y calcular la desviación estándar y varianza de una variable cuantitativa.
Hasta el momento, hemos introducido dos medidas de spread; el rango (cubierto por todos los datos) y el rango intercuartil (IQR), que mira el rango cubierto por el 50% medio de la distribución. También notamos que el IQR debe ser emparejado como medida de propagación con la mediana como medida de centro.
Pasamos ahora a otra medida del spread, la desviación estándar, que cuantifica el spread de una distribución de una manera completamente diferente.
Idea
La idea detrás de la desviación estándar es cuantificar la dispersión de una distribución midiendo qué tan lejos están las observaciones de su media. La desviación estándar da el promedio (o distancia típica) entre un punto de datos y la media.
Notación
Hay muchas notaciones para la desviación estándar: SD, s, Sd, StDev. Aquí, usaremos SD como abreviatura para la desviación estándar, y usaremos s como símbolo.
Fórmula
La fórmula de desviación estándar de la muestra es:
\(s=\sqrt{\dfrac{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}}{n-1}}\)
donde,
\(\mathrm{s}=\)muestra desviación estándar
\(\mathrm{n}=\) número de puntajes en muestra
\(\sum=\) suma de...
y media
\(\overline{\mathcal{A}}=\) de la muestra
Cálculo
Para obtener una mejor comprensión de la desviación estándar, sería útil ver un ejemplo de cómo se calcula. En la práctica, utilizaremos una computadora para hacer el cálculo.
EJEMPLO: Clientes de Video Store
A continuación se indica el número de clientes que ingresaron a una tienda de videos en 8 horas consecutivas:
7, 9, 5, 13, 3, 11, 15, 9
Para encontrar la desviación estándar del número de clientes por hora:
- Encuentra la media, barra x, de tus datos:
(7 + 9 + 5 + 13 + 3 + 11 + 15 + 9) /8 = 9
- Encuentra las desviaciones de la media:
- Las diferencias entre cada observación y la media aquí son
(7 — 9), (9 — 9), (5 — 9), (13 — 9), (3 — 9), (11 — 9), (15 — 9), (9 — 9)
-2, 0, -4, 4, -6, 2, 6, 0
- Dado que la desviación estándar intenta medir la distancia promedio (típica) entre los puntos de datos y su media, tendría sentido promediar la desviación obtenida.
- Obsérvese, sin embargo, que la suma de las desviaciones es cero.
- Este es siempre el caso, y es la razón por la que necesitamos un cálculo más complejo.
- Para resolver el problema anterior, en nuestro cálculo, cuadramos cada una de las desviaciones.
(-2) 2, (0) 2, (-4) 2, (4) 2, (-6) 2, (2) 2, (6) 2, (0) 2
4, 0, 16, 16, 36, 4, 36, 0
- Suma las desviaciones cuadradas y divida entre n — 1:
(4 + 0 + 16 + 16 + 36 + 4 + 36 + 0)/(8 — 1)
(112)/(7) = 16
- La razón por la que dividimos por n -1 se discutirá más adelante.
- Este valor, la suma de las desviaciones cuadradas divididas por n — 1, se denomina varianza. Sin embargo, la varianza no se utiliza como medida de propagación directamente ya que las unidades son el cuadrado de las unidades de los datos originales.
- La desviación estándar de los datos es la raíz cuadrada de la varianza calculada en el paso 4:
- En este caso, tenemos la raíz cuadrada de 16 que es 4. Utilizaremos la letra minúscula s para representar la desviación estándar.
s = 4
- Tomamos la raíz cuadrada para obtener una medida que está en las unidades originales de los datos. Las unidades de la varianza de 16 están en “clientes cuadrados” lo cual es difícil de interpretar.
- Las unidades de la desviación estándar están en “clientes” lo que hace que esta medida de variación sea más útil en la práctica que la varianza.
Recordemos que el promedio del número de clientes que ingresan a la tienda en una hora es de 9.
La interpretación de la desviación estándar es que en promedio, el número real de clientes que ingresan a la tienda cada hora es de 4 lejos de 9.
Comentario: La importancia de la figura numérica que encontramos en #4 anterior llamada varianza (=16 en nuestro ejemplo) será discutida mucho más adelante en el curso cuando lleguemos a la parte de inferencia.
Aprender haciendo: Desviación estándar
Propiedades de la Desviación Estándar
- Debe quedar claro a partir de la discusión hasta el momento que la SD debe emparejarse como medida de propagación con la media como medida de centro.
- Obsérvese que la única forma, matemáticamente, en la que la SD = 0, es cuando todas las observaciones tienen el mismo valor (Ej: 5, 5, 5,..., 5), en cuyo caso, las desviaciones de la media (que también es 5) son todas 0. Esto es intuitivo, ya que si todos los puntos de datos tienen el mismo valor, no tenemos variabilidad (spread) en los datos, y esperamos que la medida de spread (como la SD) sea 0. En efecto, en este caso, no sólo la SD es igual a 0, sino que el rango y el IQR también son iguales a 0. ¿Entiendes por qué?
- Al igual que la media, la SD está fuertemente influenciada por valores atípicos en los datos. Considere el ejemplo relativo a los clientes de tiendas de video: 3, 5, 7, 9, 9, 11, 13, 15 (datos ordenados). Si la observación más grande se registraba erróneamente como 150, entonces el promedio saltaría hasta 25.9, y la desviación estándar saltaría hasta SD = 50.3. Tenga en cuenta que en este sencillo ejemplo, es fácil ver que si bien la desviación estándar está fuertemente influenciada por valores atípicos, el IQR no lo es. El IQR sería el mismo en ambos casos, ya que, al igual que la mediana, el cálculo de los cuartiles depende únicamente del orden de los datos y no de los valores reales.
El último comentario lleva a la siguiente conclusión muy importante:
Elección de medidas numéricas
Objetivos de aprendizaje
LO 4.10: Elegir las medidas adecuadas para una variable cuantitativa con base en la forma de la distribución.
- Utilice la media y la desviación estándar como medidas de centro y dispersión para distribuciones razonablemente simétricas sin valores atípicos extremos.
- Para todos los demás casos, use el resumen de cinco números = min, Q1, Mediana, Q3, Max (lo que da la mediana, y fácil acceso al IQR y rango). Discutiremos el resumen de cinco números en la siguiente sección con más detalle.
Resumimos
- El rango cubierto por los datos es la medida más intuitiva de propagación y es exactamente la distancia entre el punto de datos más pequeño (min) y el más grande (Max).
- Otra medida de propagación es el rango intercuartil (IQR), que es el rango cubierto por el 50% medio de los datos.
- IQR = Q3 — Q1, la diferencia entre el tercer y el primer cuartiles.
- El primer cuartil (Q1) es el valor tal que un cuarto (25%) de los puntos de datos caen por debajo de él, o la mediana de la mitad inferior de los datos.
- El tercer cuartil (Q3) es el valor tal que tres cuartas partes (75%) de los puntos de datos caen por debajo de él, o la mediana de la mitad superior de los datos.
- El IQR se usa generalmente como medida de propagación de una distribución cuando la mediana se usa como medida del centro.
- La desviación estándar mide la dispersión reportando una distancia típica (promedio) entre los puntos de datos y su media.
- Es apropiado utilizar la desviación estándar como medida de propagación con la media como medida de centro.
- Dado que la media y las desviaciones estándar están altamente influenciadas por observaciones extremas, deben usarse como descripciones numéricas del centro y extenderse solo para distribuciones que son aproximadamente simétricas, y no tienen valores atípicos extremos. En todas las demás situaciones, preferimos el resumen de 5 números.
Medidas de Posición
CO-4: Distinguir entre diferentes escalas de medición, elegir los métodos estadísticos descriptivos e inferenciales adecuados con base en estas distinciones e interpretar los resultados.
Objetivos de aprendizaje
LO 4.4: Usando pantallas gráficas y/o medidas numéricas apropiadas, describir la distribución de una variable cuantitativa en contexto: a) describir el patrón general, b) describir desviaciones llamativas del patrón
Objetivos de aprendizaje
LO 4.14: Definir e interpretar medidas de posición (percentiles, cuartiles, resumen de cinco números, puntuaciones z).
Video
Video: Medidas de Posición (2 videos, 4:20 total)
Nota
Tutoriales SAS relacionados
- 5A — (3:01) Medidas numéricas usando PROC MEANS
Tutoriales relacionados con SPSS
- 5A — (8:00) Medidas numéricas usando EXPLORE
Aunque no es un aspecto requerido para describir distribuciones de una variable cuantitativa, a menudo nos interesa saber dónde cae un valor particular en la distribución. ¿El valor es inusualmente bajo o alto o sobre lo que esperaríamos?
Las respuestas a estas preguntas se basan en medidas de posición (o ubicación). Estas medidas dan información sobre la distribución pero también dan información sobre cómo los valores individuales se relacionan con la distribución general.
Percentiles
Una medida común de posición es el percentil. Si bien hay algunas consideraciones matemáticas involucradas en el cálculo de percentiles que no vamos a discutir, se debe tener una comprensión básica de su interpretación.
En general el percentil P-ésimo puede interpretarse como una ubicación en los datos para la cual aproximadamente P% de los otros valores en la distribución caen por debajo del percentil P-ésimo y (100 — P)% caen por encima del percentil P-ésimo.
Los cuartiles Q1 y Q3 son casos especiales de percentiles y por lo tanto son medidas de posición.
Resumen de cinco números
La combinación de los cinco números (min, Q1, M, Q3, Max) se denomina resumen de cinco números, y proporciona una descripción numérica rápida tanto del centro como del spread de una distribución.
Cada uno de los valores representa una medida de posición en el conjunto de datos.
El mínimo y el máximo proporcionan los límites y los cuartiles y la mediana proporcionando información sobre los percentiles 25, 50 y 75.
Puntuaciones estandarizadas (Puntuaciones Z)
Las puntuaciones estandarizadas, también llamadas puntuaciones z, utilizan la media y la desviación estándar como las medidas primarias de centro y propagación y, por lo tanto, son más útiles cuando la media y la desviación estándar son apropiadas, es decir, cuando la distribución es razonablemente simétrica sin valores atípicos extremos.
Para cualquier individuo, la puntuación z nos dice cuántas desviaciones estándar se desvía la puntuación bruta para ese individuo de la media y en qué dirección. Un puntaje z positivo indica que el individuo está por encima del promedio y un puntaje z negativo indica que el individuo está por debajo del promedio.
Para calcular una puntuación z, tomamos el valor individual y restamos la media y luego dividimos esta diferencia por la desviación estándar.
\(z_{i}=\dfrac{x_{i}-\bar{x}}{S}\)
Medidas de Posición
Las medidas de posición también nos permiten comparar valores de diferentes distribuciones. Por ejemplo, podemos presentar los percentiles o puntuaciones z de la estatura y el peso de un individuo. Estas dos medidas juntas proporcionarían una mejor imagen de cómo encaja el individuo en la población general que cualquiera de las dos por sí sola.
Si bien en este curso no se destacan tanto las medidas de posición como las medidas de centro y propagación, hemos visto y veremos muchas medidas de posición utilizadas en diversos aspectos de examinar la distribución de una variable y es bueno reconocerlas como medidas de posición cuando aparecen.
valores atípicos
CO-4: Distinguir entre diferentes escalas de medición, elegir los métodos estadísticos descriptivos e inferenciales adecuados con base en estas distinciones e interpretar los resultados.
Objetivos de aprendizaje
LO 4.4: Usando pantallas gráficas y/o medidas numéricas apropiadas, describir la distribución de una variable cuantitativa en contexto: a) describir el patrón general, b) describir desviaciones llamativas del patrón
Objetivos de aprendizaje
LO 4.7: Definir y describir las características de la distribución de una variable cuantitativa (forma, centro, propagación, valores atípicos).
Video
Video: Valores atípicos (2:30)
Uso del IQR para detectar valores atípicos
Objetivos de aprendizaje
LO 4.15: Definir y utilizar los criterios 1.5 (IQR) y 3 (IQR) para identificar posibles valores atípicos y valores atípicos extremos.
Hasta el momento hemos cuantificado la idea de centro, y estamos en medio de la discusión sobre medir la propagación, pero en realidad no hemos hablado de un método o regla que nos ayude a clasificar las observaciones extremas como valores atípicos. El IQR se usa comúnmente como base para una regla general para identificar valores atípicos.
El criterio 1.5 (IQR) para valores atípicos
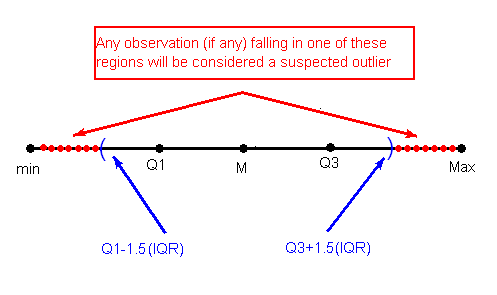
Una observación se considera un valor atípico sospechoso o un posible valor atípico si es:
- por debajo de Q1 — 1.5 (IQR) o
- por encima de Q3 + 1.5 (IQR)
La siguiente imagen (no a escala) ilustra esta regla:
EJEMPLO: Mejor Actriz Ganadora
Continuaremos con el ejemplo de ganadores del Oscar a Mejor Actriz (Enlace a los datos de los ganadores del Oscar a la Mejor Actriz).
34 34 26 37 42 41 35 31 41 33 30 74 33 49 38 61 21 41 26 80 43 29 33 35 45 49 39 34 26 25 35 33
Recordemos que cuando miramos por primera vez el histograma de edades de los ganadores del Oscar a la Mejor Actriz, hubo tres observaciones que parecían posibles valores atípicos:
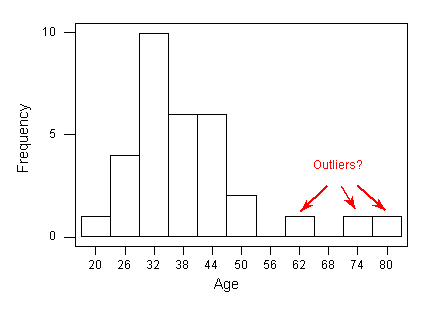
Ahora podemos usar el criterio 1.5 (IQR) para verificar si las tres edades más altas deberían clasificarse como posibles valores atípicos:
- Para este ejemplo, encontramos Q1 = 32 y Q3 = 41.5 que dan un IQR = 9.5
- Q1 — 1.5 (IQR) = 32 — (1.5) (9.5) = 17.75
- Q3 + 1.5 (IQR) = 41.5 + (1.5) (9.5) = 55.75
El criterio 1.5 (IQR) nos dice que cualquier observación con una edad inferior a 17.75 o superior a 55.75 se considera un supuesto atípico.
Por lo tanto, concluimos que las observaciones con edades de 61, 74 y 80 años deben marcarse como presuntos valores atípicos en la distribución de edades. Obsérvese que dado que la observación más pequeña es 21, no hay sospechas de valores atípicos bajos en esta distribución.
El criterio 3 (IQR) para valores atípicos
Una observación se considera un valor atípico EXTREMO si es:
- por debajo de Q1 — 3 (IQR) o
- por encima de Q3 + 3 (IQR)
EJEMPLO: Mejor Actriz Ganadora
Ahora podemos usar el criterio 3 (IQR) para verificar si alguno de los tres supuestos atípicos puede clasificarse como valores atípicos extremos:
- Para este ejemplo, encontramos Q1 = 32 y Q3 = 41.5 que dan un IQR = 9.5
- Q1 — 3 (IQR) = 32 — (3) (9.5) = 3.5
- Q3 + 3 (IQR) = 41.5 + (3) (9.5) = 70
El criterio 3 (IQR) nos dice que cualquier observación que esté por debajo de 3.5 o por encima de 70 se considera un valor atípico extremo.
Por lo tanto, concluimos que las observaciones con edades de 74 y 80 años deben marcarse como valores atípicos extremos en la distribución de edades.
Tenga en cuenta que como no hubo sospechas de valores atípicos en el extremo inferior no puede haber valores atípicos extremos en el extremo inferior de la distribución. Por lo tanto, no hubo necesidad real de que calculáramos el punto de corte bajo para valores atípicos extremos, es decir, Q1 — 3 (IQR) = 3.5.
Consulte el histograma a continuación y considere los valores atípicos individualmente.
- La observación con la edad de 62 años se encuentra visualmente mucho más cerca del centro de los datos. Podríamos tener dificultades para decidir si este valor es realmente un valor atípico usando solo esta gráfica.
- Sin embargo, las edades de 74 y 80 están claramente lejos del grueso de la distribución. Podríamos sentirnos muy cómodos decidiendo que estos valores son valores atípicos basados únicamente en la gráfica.
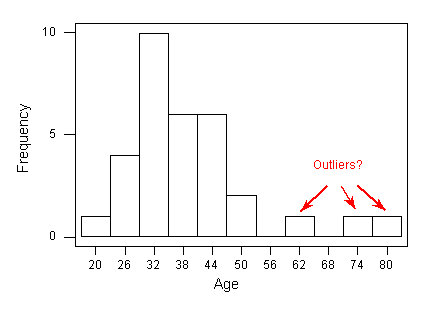
¿Recibí esto? : Identificación de valores atípicos mediante el método IQR
Comprender los valores atípicos
Objetivos de aprendizaje
LO 4.16: Discutir posibles métodos para manejar valores atípicos en la práctica.
Simplemente practicamos una forma de 'marcar' posibles valores atípicos. ¿Por qué es importante identificar posibles valores atípicos y cómo deben abordarse? Las respuestas a estas preguntas dependen de las razones de los valores periféricos. Aquí hay varias posibilidades:
- A pesar de que es un valor extremo, si se puede entender que un valor atípico ha sido producido esencialmente por el mismo tipo de proceso físico o biológico que el resto de los datos, y si se espera que tales valores extremos eventualmente vuelvan a ocurrir, entonces tal valor atípico indica algo importante e interesante sobre el proceso que estás investigando, y debe conservarse en los datos.
- Si se puede explicar que un valor atípico se ha producido bajo condiciones fundamentalmente diferentes del resto de los datos (o por un proceso fundamentalmente diferente), dicho valor atípico puede eliminarse de los datos si tu objetivo es investigar solo el proceso que produjo el resto del datos.
- Un valor atípico puede indicar un error en los datos (como un error tipográfico, o un error de medición), en cuyo caso debe corregirse si es posible o bien eliminarse de los datos antes de calcular estadísticas resumidas o hacer inferencias a partir de los datos (y el motivo del error debe ser investigado).
Aquí hay ejemplos de cada uno de estos tipos de valores atípicos:
- El siguiente histograma muestra la magnitud de 460 sismos en California, ocurridos en el año 2000, entre el 28 de agosto y el 9 de septiembre:
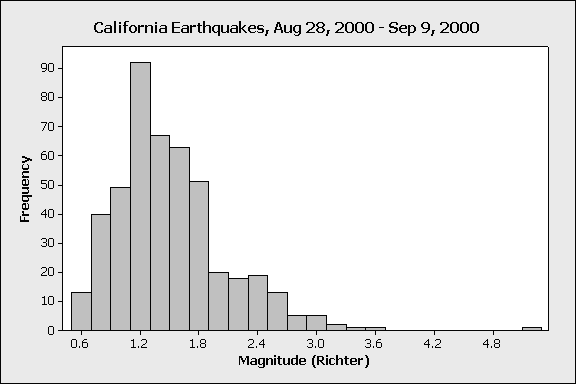
Identificando el valor atípico: En el extremo extremo derecho de la pantalla (más allá de 4.8), vemos una barra baja; esto representa un sismo (porque la barra tiene altura de 1) que fue mucho más severo que los demás en los datos.
Entendiendo el valor atípico: En este caso, el valor atípico representa un sismo mucho más fuerte, que es relativamente más raro que los sismos más pequeños que ocurren con más frecuencia en California.
Cómo manejar lo atípico: Para muchos propósitos, los terremotos relativamente severos que representa el valor atípico podrían ser los más importantes (porque, por ejemplo, ese tipo de sismo tiene el potencial de hacer más daño a las personas y a la infraestructura). Los temblores de menor magnitud podrían no hacer ningún daño, o incluso sentirse en absoluto. Entonces, para muchos fines podría ser importante mantener este valor atípico en los datos.
2. El siguiente histograma muestra el porcentaje de retorno mensual sobre las acciones de Phillip Morris (una gran compañía tabacalera) de julio de 1990 a mayo de 1997:
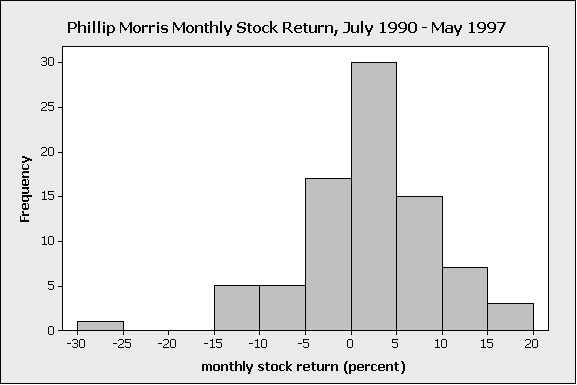
Identificando el valor atípico: En la pantalla, vemos una barra baja muy a la izquierda de las demás; esto representa el retorno de un mes (porque la barra tiene altura de 1), donde el valor de las acciones de Phillip Morris era inusualmente bajo.
Entendiendo el valor atípico: La explicación de este valor atípico en particular es que, a principios de la década de 1990, se estaban llevando a cabo audiencias federales muy publicitadas sobre la adicción al tabaquismo, y hubo un creciente sentimiento público contra las tabacaleras. El valor mensual inusualmente bajo en el conjunto de datos de Phillip Morris se debió a la presión pública contra el tabaquismo, lo que afectó negativamente las acciones de la compañía para ese mes en particular.
Cómo manejar el valor atípico: En este caso, el valor atípico se debió a condiciones inusuales durante un mes en particular que no se espera que se repitan, y que fueron fundamentalmente diferentes a las condiciones que produjeron los valores en todos los demás meses. Entonces en este caso, sería razonable eliminar el valor atípico, si quisiéramos caracterizar el “típico” retorno mensual de las acciones de Phillip Morris.
3. Cuando los arqueólogos desentierran objetos como piezas de cerámica antigua, se pueden realizar análisis químicos en los artefactos. El contenido químico de la cerámica puede variar dependiendo del tipo de arcilla así como de la técnica de fabricación particular. El siguiente histograma muestra los resultados de uno de esos análisis químicos reales, realizado en 48 artefactos antiguos de cerámica romana de sitios arqueológicos en Gran Bretaña:
![Un histograma titulado “Contenido de óxido manganoso en una muestra de cerámica romana antigua”. El eje X está etiquetado como “número de fragmentos de cerámica”, y oscila entre 0 y 20. El eje Y está etiquetado como “contenido de óxido manganoso [MnO]” y oscila entre 0.0 y 0.4. El histograma está sesgado a la derecha. Aquí están las barras: x=0.0, y=10; x=0.05, y=13; x=0.1, y=18; x=0.15, y=5; x=0.20, y=1; x=0.4, y=1. Tenga en cuenta que no hay fragmentos para x=0.25 a x=0.35 Un histograma titulado “Contenido de óxido manganoso en una muestra de cerámica romana antigua”. El eje X está etiquetado como “número de fragmentos de cerámica”, y oscila entre 0 y 20. El eje Y está etiquetado como “contenido de óxido manganoso [MnO]” y oscila entre 0.0 y 0.4. El histograma está sesgado a la derecha. Aquí están las barras: x=0.0, y=10; x=0.05, y=13; x=0.1, y=18; x=0.15, y=5; x=0.20, y=1; x=0.4, y=1. Tenga en cuenta que no hay fragmentos para x=0.25 a x=0.35](https://stats.libretexts.org/@api/deki/files/19723/images-mod1-spread23.gif)
Como aparecieron en Tubb, et al. (1980). “El análisis de la cerámica romano-británica por espectrofotometría de absorción atómica”. Arqueometría, vol. 22, reimpreso en Estadística en Arqueología por Michael Baxter, p. 21.
Identificando el valor atípico: En la pantalla, vemos una barra baja muy a la derecha de las demás; esto representa una pieza de cerámica (porque la barra tiene una altura de 1), que tiene un valor sospechosamente alto de óxido manganoso.
Entendiendo el valor atípico: A partir de la comparación con otras piezas de cerámica encontradas en el mismo sitio, y con base en la comprensión experta del contenido típico de este compuesto en particular, se concluyó que el valor inusualmente alto probablemente fue un error tipográfico que se hizo cuando se publicaron los datos en el artículo original de 1980 (se mecanografió como “.394” pero probablemente estaba destinado a ser “.094”).
Cómo manejar el valor atípico: En este caso, dado que el valor atípico fue juzgado como un error, se debe eliminar de los datos antes de un análisis posterior. De hecho, eliminar el valor atípico es útil no sólo porque es un error, sino también porque hacerlo revela una estructura importante que de otra manera estaba oculta. Esta característica es evidente en la siguiente pantalla:
![Un histograma titulado "Histograma sin el valor atípico” El eje Y se etiqueta como “número de fragmentos de cerámica”, y oscila entre 0 y 12. El eje X está etiquetado como “contenido de óxido manganoso [MnO]” y oscila entre 0.00 y aproximadamente 0.18. Ir de izquierda a derecha a lo largo del eje X revela que a x=0, hay una frecuencia de 10. Entonces, no hay barras hasta x=0.4. A partir de aquí las barras aumentan en altura hasta x=0.08, donde la frecuencia es 12. Entonces las barras comienzan a disminuir. Un histograma titulado "Histograma sin el valor atípico” El eje Y se etiqueta como “número de fragmentos de cerámica”, y oscila entre 0 y 12. El eje X está etiquetado como “contenido de óxido manganoso [MnO]” y oscila entre 0.00 y aproximadamente 0.18. Ir de izquierda a derecha a lo largo del eje X revela que a x=0, hay una frecuencia de 10. Entonces, no hay barras hasta x=0.4. A partir de aquí las barras aumentan en altura hasta x=0.08, donde la frecuencia es 12. Entonces las barras comienzan a disminuir.](https://stats.libretexts.org/@api/deki/files/19726/images-mod1-spread24.gif)
Cuando se elimina el valor atípico, se vuelve a escalar la pantalla para que ahora podamos ver el conjunto de 10 piezas de cerámica que casi no tenían óxido manganoso. Estas 10 piezas podrían haber sido hechas con una técnica de encapsulado diferente, por lo que identificarlas como diferentes del resto es históricamente útil. Esta característica solo fue evidente después de que se eliminó el valor atípico.
Leyendo: Valores atípicos (≈ 1400 palabras)
Parcelas de caja
CO-4: Distinguir entre diferentes escalas de medición, elegir los métodos estadísticos descriptivos e inferenciales adecuados con base en estas distinciones e interpretar los resultados.
Objetivos de aprendizaje
LO 4.4: Usando pantallas gráficas y/o medidas numéricas apropiadas, describir la distribución de una variable cuantitativa en contexto: a) describir el patrón general, b) describir desviaciones llamativas del patrón
Objetivos de aprendizaje
LO 4.7: Definir y describir las características de la distribución de una variable cuantitativa (forma, centro, propagación, valores atípicos).
Video
Vídeo: Boxplots (2 vídeos, 7:02 total)
Nota
Tutoriales SAS relacionados
Tutoriales relacionados con SPSS
- 5B — (2:29) Creación de histogramas y gráficas de caja
Introducción
Ahora introducimos otra visualización gráfica de la distribución de una variable cuantitativa, la gráfica de caja.
Resumen de los cinco números
Hasta el momento, en nuestra discusión sobre las medidas de propagación, algunos actores clave fueron:
- los extremos (min y Max), que proporcionan el rango cubierto por todos los datos; y
- los cuartiles (Q1, M y Q3), que en conjunto proporcionan el IQR, el rango cubierto por el 50% medio de los datos.
Recordemos que la combinación de los cinco números (min, Q1, M, Q3, Max) se denomina resumen de cinco números, y proporciona una descripción numérica rápida tanto del centro como del spread de una distribución.
EJEMPLO: Mejor Actriz Ganadora
Continuaremos con el ejemplo de ganadores del Oscar a Mejor Actriz (Enlace a los datos de los ganadores del Oscar a la Mejor Actriz).
34 34 26 37 42 41 35 31 41 33 30 74 33 49 38 61 21 41 26 80 43 29 33 35 45 49 39 34 26 25 35 33
El resumen de cinco números de la era de los ganadores del Oscar a Mejor Actriz (1970-2001) es:
min = 21, Q1 = 32, M = 35, Q3 = 41.5, Máx = 80
Para bosquejar la gráfica de caja necesitaremos conocer el resumen de 5 números así como identificar cualquier valor atípico. También necesitaremos ubicar los valores más grandes y más pequeños que no sean valores atípicos. El stemplot a continuación podría ser útil ya que muestra los datos en orden.
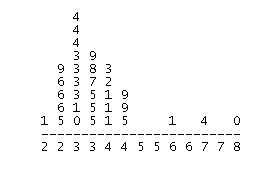
Aprende haciendo: Resumen de 5 números
Ahora que entiendes lo que significa cada uno de los cinco números, puedes apreciar cuánta información sobre la distribución está empaquetada en el resumen de cinco números. Toda esta información también se puede representar visualmente mediante el uso de la gráfica de caja.
El Boxplot
Objetivos de aprendizaje
LO 4.17: Explicar el proceso de creación de una gráfica de caja (incluyendo la indicación apropiada de valores atípicos).
La gráfica de caja representa gráficamente la distribución de una variable cuantitativa al mostrar visualmente el resumen de cinco números y cualquier observación que se clasifique como un supuesto atípico utilizando el criterio 1.5 (RIC).
EJEMPLO: Construir un diagrama de caja
(Enlace a los datos de los ganadores del Oscar a la Mejor Actriz).
- La caja central abarca de Q1 a Q3. En nuestro ejemplo, la caja abarca de 32 a 41.5. Tenga en cuenta que el ancho de la caja no tiene sentido.
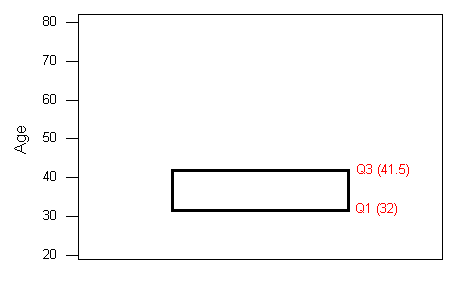
2. Una línea en la caja marca la mediana M, que en nuestro caso es 35.
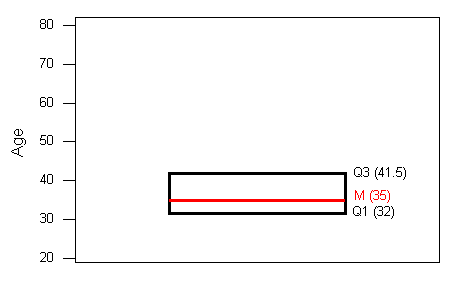
3. Las líneas se extienden desde los bordes de la caja hasta las observaciones más pequeñas y mayores que no se clasificaron como supuestos atípicos (utilizando el criterio 1.5XiQR). En nuestro ejemplo, no tenemos valores atípicos bajos, por lo que la línea de fondo baja a la observación más pequeña, que es 21. Dado que tenemos tres valores atípicos altos (61,74, y 80), la línea superior se extiende solo hasta 49, que es la observación más grande que no se ha marcado como un valor atípico.
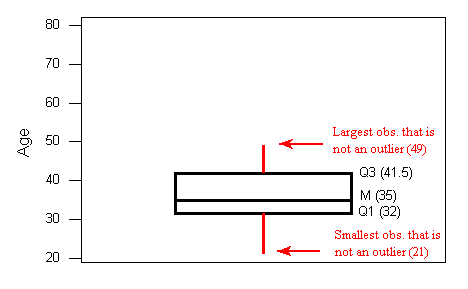
4. los valores atípicos están marcados con asteriscos (*).
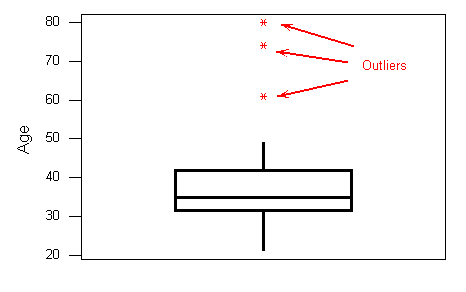
Para resumir: la siguiente información se representa visualmente en la gráfica de caja:
- el resumen de cinco números (azul)
- la gama y IQR (rojo)
- valores atípicos (verde)
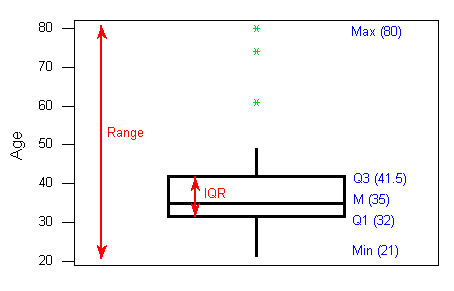
Aprende haciendo: Boxplots
¿Recibí esto? : Parcelas de caja
Diagramas de caja lado a lado (comparativos)
Objetivos de aprendizaje
LO 4.18: Comparar y contrastar distribuciones (de datos cuantitativos) de dos o más grupos, y producir un breve resumen, interpretando sus hallazgos en contexto.
Como aprendimos anteriormente, la distribución de una variable cuantitativa se representa mejor gráficamente por un histograma. Las gráficas de caja son más útiles cuando se presentan lado a lado para comparar y contrastar distribuciones de dos o más grupos.
EJEMPLO: Mejor Actriz/Actor Ganadores del
Hasta el momento hemos examinado las distribuciones por edades de los ganadores del Oscar para hombres y mujeres por separado. Será interesante comparar las distribuciones por edades de actores y actrices que ganaron los Oscar de mejor actuación. Para ello veremos las tramas de caja lado a lado de las distribuciones de edad por género.
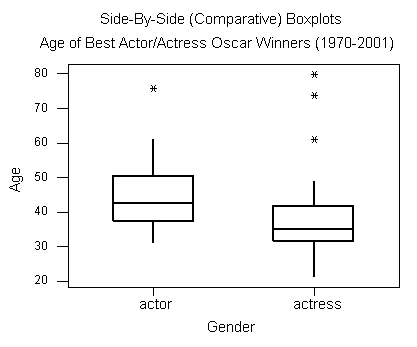
Recordemos también que encontramos el resumen de cinco números y las medias para ambas distribuciones. Para el conjunto de datos de Mejor Actriz, hicimos los cálculos a mano. Para el conjunto de datos de Best Actor, utilizamos software estadístico, y aquí están los resultados:
- Actores: min = 31, Q1 = 37.25, M = 42.5, Q3 = 50.25, Max = 76
- Actrices: min = 21, Q1 = 32, M = 35, Q3 = 41.5, Máx = 80
Con base en la gráfica y las medidas numéricas, podemos hacer la siguiente comparación entre las dos distribuciones:
Centro: La gráfica revela que la distribución por edad de los varones es mayor que la distribución por edad de las mujeres. Esto se sustenta en las medidas numéricas. La mediana de edad para las mujeres (35) es menor que para los hombres (42.5). En realidad, cabe señalar que incluso el tercer cuartil de la distribución femenina (41.5) es menor que la mediana de edad para los varones. Por ello concluimos que en general, las actrices ganan el Oscar a la Mejor Actriz a una edad más joven que los actores.
Spread: A juzgar por el rango de los datos, hay mucha más variabilidad en la distribución de las mujeres (rango = 59) que en la distribución masculina (rango = 45). Por otro lado, si nos fijamos en el IQR, que mide la variabilidad solo entre el 50% medio de la distribución, vemos más propagación en las edades de los machos (IQR = 13) que en las hembras (IQR = 9.5). Concluimos que entre todos los ganadores, las edades de los actores son más parecidas que las de las actrices. Sin embargo, el 50% de la distribución por edades de las actrices es más homogénea que la distribución por edades de los actores.
Valores atípicos: Vemos que tenemos valores atípicos en ambas distribuciones. Solo hay un alto valor atípico en la distribución de los actores (76, Henry Fonda, On Golden Pond), en comparación con tres valores atípicos altos en la distribución de las actrices.
EJEMPLO: Temperatura de Pittsburg vs San Francisco
Para comparar las altas temperaturas promedio de Pittsburgh con las de San Francisco, veremos las siguientes parcelas de caja lado a lado, y complementaremos la gráfica con los estadísticos descriptivos de cada una de las dos distribuciones.
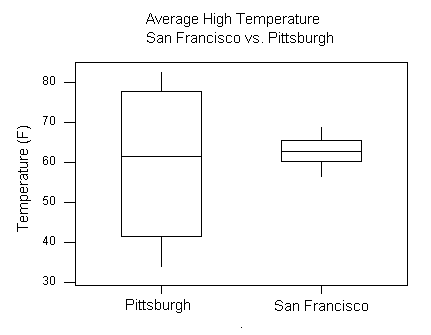
| Estadística | Pittsburgh | San Francisco |
|---|---|---|
| min | 33.7 | 56.3 |
| Q1 | 41.2 | 60.2 |
| Mediana | 61.4 | 62.7 |
| Q3 | 77.75 | 65.35 |
| Max | 82.6 | 68.7 |
Al mirar la gráfica, las similitudes y diferencias entre las dos distribuciones son llamativas. Ambas distribuciones tienen aproximadamente el mismo centro (las medianas son 61.4 para Pitt y 62.7 para San Francisco). Sin embargo, las temperaturas en Pittsburgh tienen una variabilidad mucho mayor que las temperaturas en San Francisco (Rango: 49 vs. 12. IQR: 36.5 vs. 5).
La interpretación práctica de los resultados que obtuvimos es que el clima en San Francisco es mucho más consistente que el clima en Pittsburgh, que varía mucho durante el año. Además, debido a que las temperaturas en San Francisco varían muy poco durante el año, saber que la temperatura media es alrededor de 63 es en realidad muy informativo. Por otro lado, saber que la temperatura media en Pittsburgh es alrededor de 61 es prácticamente inútil, ya que las temperaturas varían tanto durante el año, y pueden llegar a ser mucho más cálidas o mucho más frías.
Tenga en cuenta que este ejemplo proporciona más intuición sobre la variabilidad al interpretar la variabilidad pequeña como consistencia, y la variabilidad grande como falta de consistencia. También, a través de este ejemplo aprendimos que el centro de la distribución es más significativo como valor típico para la distribución cuando hay poca variabilidad (o, como dicen los estadísticos, poco “ruido”) a su alrededor. Cuando hay gran variabilidad, el centro pierde su significado práctico como valor típico.
Aprender haciendo: Comparando distribuciones con gráficas de caja
Resumimos
- El resumen de cinco números de una distribución consiste en la mediana (M), los dos cuartiles (Q1, Q3) y los extremos (min, Max).
- El resumen de cinco números proporciona una descripción numérica completa de una distribución. La mediana describe el centro, y los extremos (que dan el rango) y los cuartiles (que dan el IQR) describen la propagación.
- La gráfica de caja representa gráficamente la distribución de una variable cuantitativa al mostrar visualmente el resumen de cinco números y cualquier observación que se clasifique como un supuesto atípico utilizando el criterio 1.5 (IQR). (Algunos paquetes de software indican valores atípicos extremos con un símbolo diferente)
- Las gráficas de caja son más útiles cuando se presentan lado a lado para comparar y contrastar distribuciones de dos o más grupos.
La forma “normal”
CO-4: Distinguir entre diferentes escalas de medición, elegir los métodos estadísticos descriptivos e inferenciales adecuados con base en estas distinciones e interpretar los resultados.
CO-6: Aplicar conceptos básicos de probabilidad, variación aleatoria y distribuciones de probabilidad estadística de uso común.
Objetivos de aprendizaje
LO 4.4: Usando pantallas gráficas y/o medidas numéricas apropiadas, describir la distribución de una variable cuantitativa en contexto: a) describir el patrón general, b) describir desviaciones llamativas del patrón
Objetivos de aprendizaje
LO 4.7: Definir y describir las características de la distribución de una variable cuantitativa (forma, centro, propagación, valores atípicos).
Video
Video: La forma normal (5:34)
Tutoriales SAS relacionados
- 5B — (4:05) Creación de Histogramas y Gráficas de Caja usando SGPLOT
- 5C — (5:41) Crear gráficas QQ y otras gráficas usando UNIVARIATE
Tutoriales relacionados con SPSS
- 5B — (2:29) Creación de histogramas y gráficas de caja
- 5C — (2:31) Creación de gráficas QQ y Pp-plots
La regla de desviación estándar
Objetivos de aprendizaje
LO 6.2: Aplicar la regla de desviación estándar al caso especial de distribuciones que tengan la forma “normal”.
En la actividad anterior intentamos ayudarte a desarrollar una mejor intuición sobre el concepto de desviación estándar. La regla que estamos a punto de presentar, llamada “La regla de la desviación estándar” (también conocida como “La regla empírica”), ojalá también contribuya a construir tu intuición sobre este concepto.
Considere una distribución simétrica en forma de montículo:
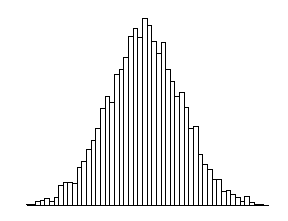
Para distribuciones que tengan esta forma (posteriormente definiremos esta forma como “normalmente distribuida”), se aplica la siguiente regla:
La regla de desviación estándar:
- Aproximadamente 68% de las observaciones se encuentran dentro de 1 desviación estándar de la media.
- Aproximadamente el 95% de las observaciones se encuentran dentro de 2 desviaciones estándar de la media.
- Aproximadamente 99.7% (o prácticamente todas) de las observaciones se encuentran dentro de 3 desviaciones estándar de la media.
La siguiente imagen ilustra esta regla:
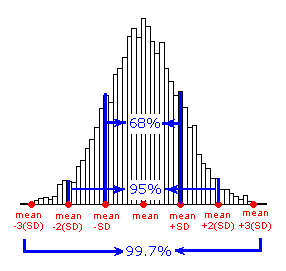
Esta regla proporciona otra forma de interpretar la desviación estándar de una distribución, y así también proporciona un poco más de intuición al respecto.
Applet Interactivo: La Regla de Desviación Estándar
Para ver cómo funciona esta regla en la práctica, considere el siguiente ejemplo:
Ejemplo: ALTURA MACHO
El siguiente histograma representa la altura (en pulgadas) de 50 machos. Tenga en cuenta que los datos son aproximadamente normales, por lo que nos gustaría ver cómo funciona la Regla de Desviación Estándar para este ejemplo.
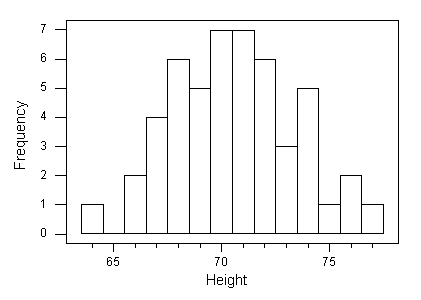
A continuación se presentan los datos reales, y las medidas numéricas de la distribución. Tenga en cuenta que los actores clave aquí, la media y la desviación estándar, han sido resaltados.
| Estadística | Altura |
|---|---|
| N | 50 |
| Media | 70.58 |
| StDev | 2.858 |
| min | 64 |
| Q1 | 68 |
| Mediana | 70.5 |
| Q3 | 72 |
| Max | 77 |
Para ver qué tan bien funciona la Regla de Desviación Estándar para este caso, encontraremos qué porcentaje de las observaciones se encuentra dentro de 1, 2 y 3 desviaciones estándar de la media, y compararlo con lo que la Regla de Desviación Estándar nos dice que debe ser este porcentaje.

Resulta que la Regla de Desviación Estándar funciona muy bien en este ejemplo.
El siguiente ejemplo ilustra cómo podemos aplicar la Regla de Desviación Estándar a variables cuya distribución se sabe que es aproximadamente normal.
EJEMPLO: Duración del Embarazo Humano
La duración del embarazo humano no es fija. Se sabe que varía según una distribución que es aproximadamente normal, con una media de 266 días, y una desviación estándar de 16 días. (Fuente: Las cifras son de Moore y McCabe, Introducción a la práctica de la estadística).
Primero, apliquemos la Regla de Desviación Estándar a este caso dibujando una imagen:
![Un histograma. El eje X está etiquetado como “Longitud (días)”, y oscila entre 214 y 314 días. El modo y la media del histograma están en x=266. La 1ª Desviación Estándar, o la media 68%, abarca el rango [250,282]. La 2ª Desviación Estándar (media 95%) abarca el rango [234,298]. La 3ª Desviación Estándar (media 99.7%) abarca el rango [218,314]. Un histograma. El eje X está etiquetado como “Longitud (días)”, y oscila entre 214 y 314 días. El modo y la media del histograma están en x=266. La 1ª Desviación Estándar, o la media 68%, abarca el rango [250,282]. La 2ª Desviación Estándar (media 95%) abarca el rango [234,298]. La 3ª Desviación Estándar (media 99.7%) abarca el rango [218,314].](https://stats.libretexts.org/@api/deki/files/19666/images-mod1-sdgraph4.gif)
- Pregunta: ¿Cuánto dura la mitad del 95% de los embarazos humanos? Ahora podemos utilizar la información proporcionada por la Regla de Desviación Estándar sobre la distribución de la duración del embarazo humano, para responder algunas preguntas. Por ejemplo:
- Respuesta: El 95% medio de los embarazos duran dentro de 2 desviaciones estándar de la media, o en este caso 234-298 días.
- Pregunta: ¿Qué porcentaje de embarazos duran más de 298 días?
- Respuesta: Para responder a esto considera la siguiente imagen:
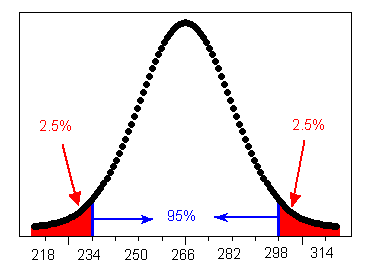
- Pregunta: ¿Qué tan cortos son los 2.5% más cortos de los embarazos? Dado que el 95% de los embarazos duran entre 234 y 298 días, el 5% restante de los embarazos duran menos de 234 días o más de 298 días. Dado que la distribución normal es simétrica, estos 5% de los embarazos se dividen equitativamente entre las dos colas, y por lo tanto 2.5% de los embarazos duran más de 298 días.
- Respuesta: Utilizando el mismo razonamiento que en la pregunta anterior, el 2.5% más corto de los embarazos humanos duran menos de 234 días.
- Pregunta: ¿Qué porcentaje de embarazos humanos duran más de 266 días?
- Respuesta: Ya que 266 días es la media, aproximadamente el 50% de los embarazos duran más de 266 días.
Aquí hay una imagen completa de la información proporcionada por la regla de desviación estándar.
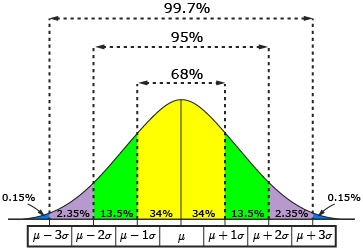
¿Recibí esto? : Regla de Desviación Estándar
Métodos Visuales de Evaluación de la Normalidad
Objetivos de aprendizaje
LO 6.3: Utilizar histogramas y gráficas QQ (o Gráficas de Probabilidad Normal) para evaluar visualmente la normalidad de distribuciones de variables cuantitativas.
La distribución normal existe en teoría pero rara vez, si alguna vez, en la vida real. Los histogramas proporcionan una excelente visualización gráfica para ayudarnos a evaluar la normalidad. Podemos agregar una “curva normal” al histograma que muestra la distribución normal teniendo la misma media y desviación estándar que nuestra muestra. Cuanto más se ajuste el histograma a esta curva, más (perfectamente) normal será la muestra.
En los ejemplos siguientes, la gráfica en la parte superior está aproximadamente distribuida normalmente mientras que la gráfica de la parte inferior está claramente sesgada a la derecha.
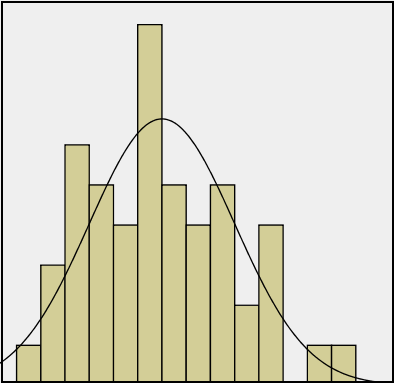
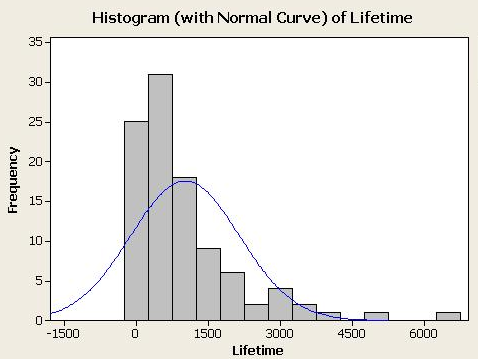
Desafortunadamente, no podemos determinar cuantitativamente hasta qué punto la distribución se distribuye normalmente o no utilizando este método, pero puede ser útil para hacer juicios cualitativos sobre si los datos se aproximan a la curva normal.
Otra gráfica común para evaluar la normalidad es la gráfica Q-Q (o Gráfica de Probabilidad Normal). En estas gráficas, se trazan los percentiles o cuantiles de la distribución teórica (en este caso la distribución normal estándar) frente a los de los datos. Si los datos coinciden con la distribución teórica, la gráfica dará como resultado una línea recta. La gráfica siguiente muestra una distribución que sigue de cerca un modelo normal.
Nota: Las gráficas QQ no son diagramas de dispersión (que analizaremos pronto), solo muestran información sobre una variable cuantitativa y la grafican contra los valores teóricos o esperados de una distribución normal con la misma media y desviación estándar que nuestros datos. También se pueden utilizar otras distribuciones.
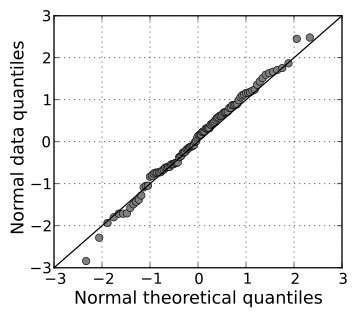
En la mayoría de los casos las distribuciones que encuentres solo serán aproximaciones de la curva normal, ¡o no se parecerán en absoluto a la distribución normal! Sin embargo, puede ser importante considerar qué tan bien los datos analizados se aproximan a la curva normal ya que esta distribución es un supuesto clave de muchos análisis estadísticos.
Aquí hay algunos ejemplos más:
EJEMPLO: Algunos datos reales
A continuación se presenta la gráfica QQ, histograma y diagrama de caja para variables de un conjunto de datos de una población de mujeres que tenían al menos 21 años de edad, de ascendencia india pima y residentes cerca de Phoenix, Arizona, a las que se les realizó la prueba de diabetes según criterios de la Organización Mundial de la Salud. Los datos fueron recolectados por el Instituto Nacional de Diabetes y Enfermedades Digestivas y Renales de Estados Unidos. Se utilizaron los 532 registros completos después de dejar caer los datos (principalmente faltantes) sobre la insulina sérica.
El Índice de Masa Corporal es definitivamente unimodal y simétrico y podría provenir fácilmente de una población que normalmente se distribuye.
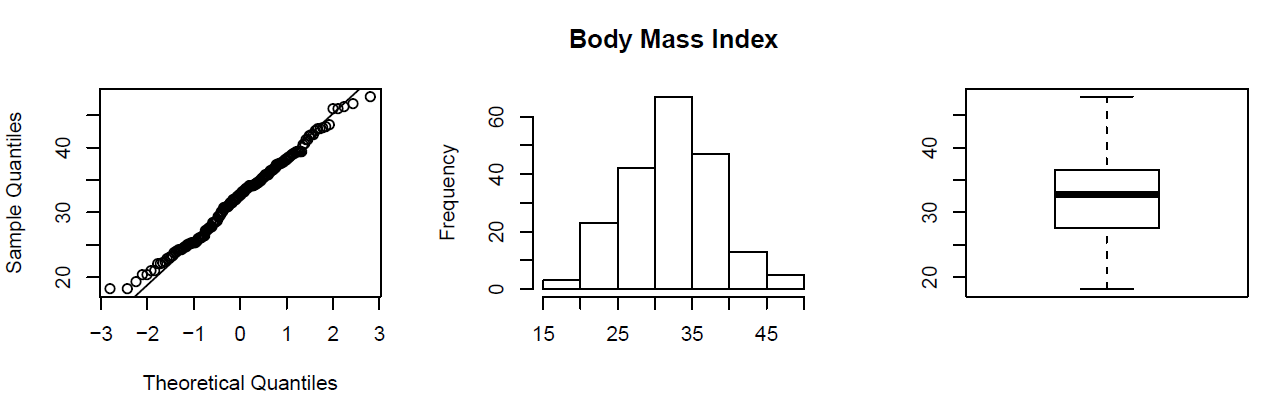
Las puntuaciones de Diabetes Pedigree Function fueron unimodales y sesgadas a la derecha. Estos datos no parecen provenir de una población que normalmente se distribuye.
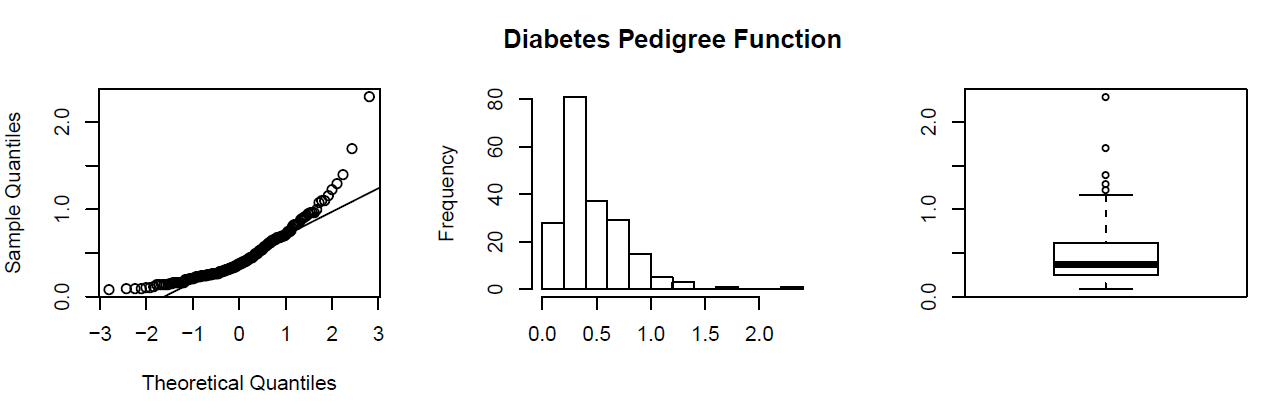
El grosor del pliegue cutáneo del tríceps es básicamente simétrico con un valor atípico extremo (y un valor atípico potencial pero leve).
Tenga cuidado de no llamar a tal distribución “derecha sesgada” ya que es solo el único valor atípico lo que realmente muestra ese patrón aquí. Como mínimo, elimine el valor atípico y vuelva a crear las gráficas para ver qué tan sesgada podría estar el resto de los datos.
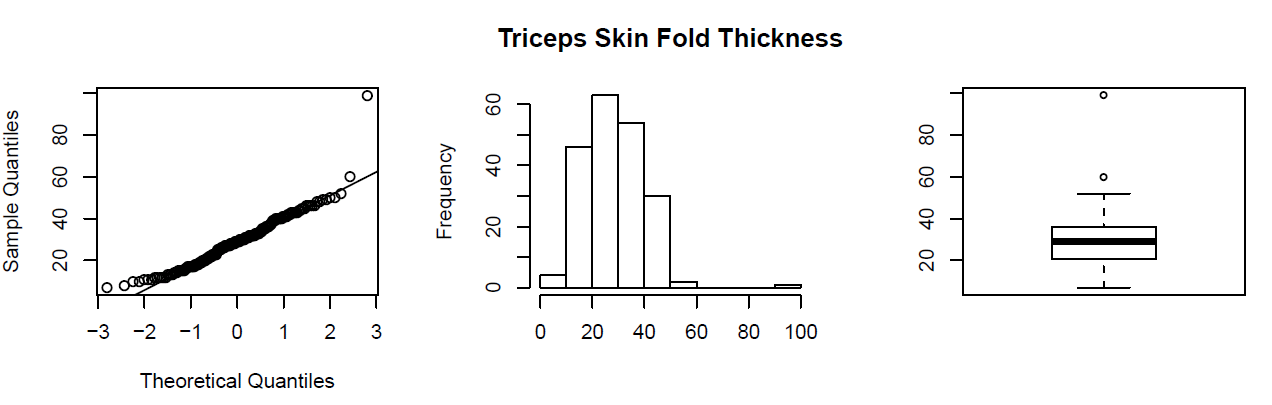
EJEMPLO: Datos generados aleatoriamente
Como no había ejemplos de izquierda sesgada en los datos reales, aquí hay dos distribuciones izquierdas sesgadas generadas aleatoriamente. Observe que el primero está menos sesgado a la izquierda que el segundo y esto se indica claramente en las tres parcelas.
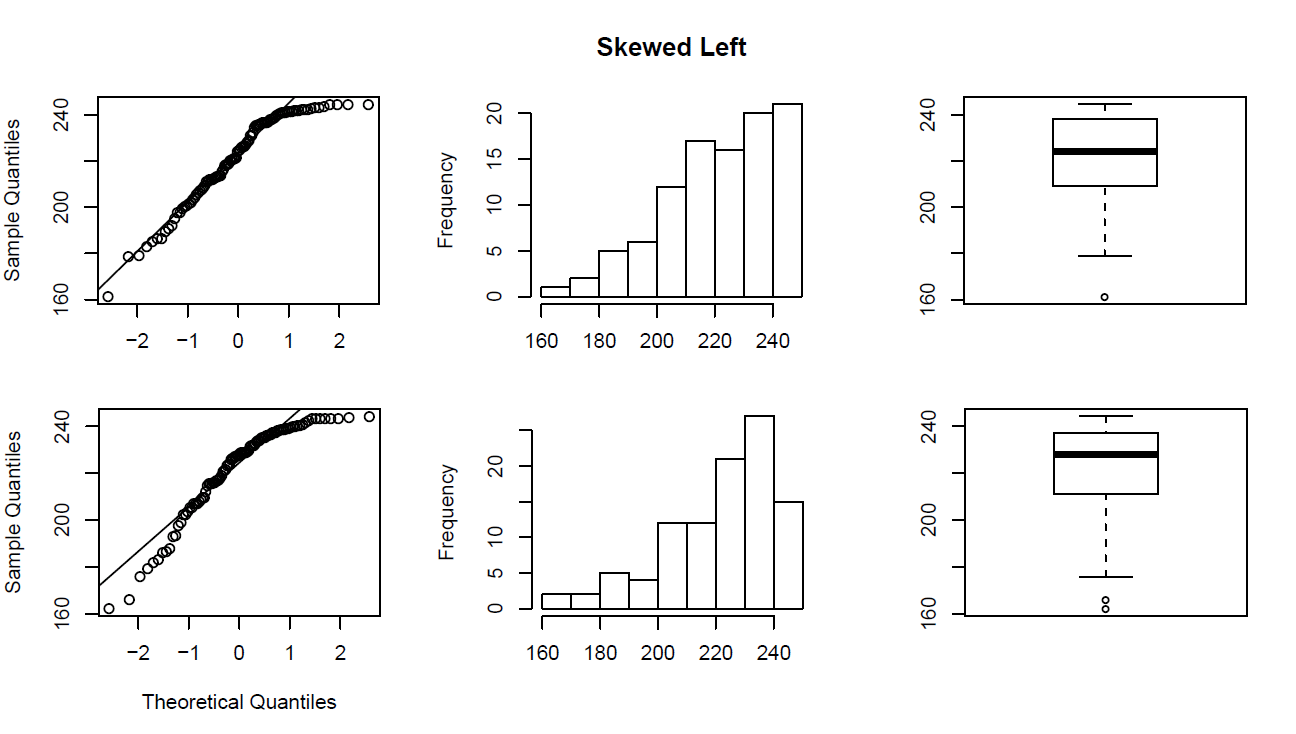
Comentarios:
- Aunque la población esté exactamente distribuida normalmente, las muestras de esta población pueden parecer no normales especialmente para tamaños de muestra pequeños. Consulte este documento que contiene 21 muestras de tamaño n = 50 de una distribución normal con una media de 200 y una desviación estándar de 30. Se resaltan las muestras que producen resultados que están sesgados o aparentemente no normales, pero incluso entre las que no están resaltadas, notan la variación en las formas vistas: Muestras normales
- La regla de desviación estándar también puede ayudar a evaluar la normalidad, ya que cuanto más cerca esté el porcentaje de puntos de datos dentro de 1, 2 y 3 desviaciones estándar del de la regla, cuanto más cerca se ajusten los datos a una distribución normal.
- En nuestro ejemplo de alturas masculinas, vemos que el histograma se asemeja a una distribución normal y los porcentajes de muestra son muy cercanos a lo predicho por la regla de desviación estándar.
¿Recibí esto? : Evaluar la normalidad
(Opcional) Lectura: La distribución normal (≈ 500 palabras)
Puntuaciones estandarizadas (Puntuaciones Z)
Objetivos de aprendizaje
LO 4.14: Definir e interpretar medidas de posición (percentiles, cuartiles, resumen de cinco números, puntuaciones z).
Ya hemos aprendido la regla de desviación estándar, que para los datos normalmente distribuidos, proporciona aproximaciones para la proporción de valores de datos dentro de 1, 2 y 3 desviaciones estándar. De esto sabemos que aproximadamente 5% de los valores de los datos se esperaría que cayeran FUERA DE 2 desviaciones estándar.
Si calculamos las puntuaciones estandarizadas (o puntuaciones z) para nuestros datos, sería fácil identificar estos valores inusualmente grandes o pequeños en nuestros datos. Para calcular una puntuación z, recordemos que tomamos el valor individual y restamos la media y luego dividimos esta diferencia por la desviación estándar.
\(z_{i}=\dfrac{x_{i}-\bar{x}}{S}\)
Para cualquier individuo, la puntuación z nos dice cuántas desviaciones estándar se desvía la puntuación bruta para ese individuo de la media y en qué dirección. Un puntaje z positivo indica que el individuo está por encima del promedio y un puntaje z negativo indica que el individuo está por debajo del promedio.
Comentarios:
- Los puntajes estandarizados se pueden utilizar para ayudar a identificar posibles valores atípicos
- Para distribuciones aproximadamente normales, las puntuaciones z mayores de 2 o menores de -2 son raras (ocurrirán aproximadamente el 5% de las veces).
- Para cualquier distribución, las puntuaciones z mayores de 4 o menores de -4 son raras (ocurrirán menos de 6.25% de las veces).
- Las puntuaciones estandarizadas, junto con otras medidas de posición, son útiles al comparar individuos en diferentes conjuntos de datos ya que la comparación toma en cuenta la posición relativa de los individuos en su conjunto de datos. Con las puntuaciones z, podemos decir qué individuo tiene una posición relativamente mayor o menor en su respectivo conjunto de datos.
- Más adelante en el curso, veremos que esta idea de estandarización se utiliza a menudo en los análisis estadísticos.
EJEMPLO: Mejor Actriz Ganadora
Continuaremos con el ejemplo de ganadores del Oscar a Mejor Actriz (Enlace a los datos de los ganadores del Oscar a la Mejor Actriz).
34 34 26 37 42 41 35 31 41 33 30 74 33 49 38 61 21 41 26 80 43 29 33 35 45 49 39 34 26 25 35 33
En ejemplos anteriores, identificamos tres observaciones como valores atípicos, dos de los cuales se clasificaron como valores atípicos extremos (edades de 61, 74 y 80 años)
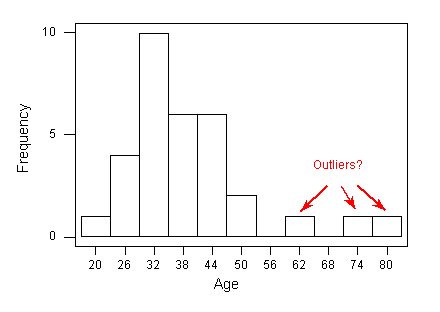
La media de esta muestra es 38.5 y la desviación estándar es 12.95.
- El puntaje z para la actriz con edad = 80 es
\(z=\dfrac{80-38.5}{12.95} = 3.20\)
Así, entre nuestras ganadoras del Oscar femeninas de nuestra muestra, esta actriz es 3.20 desviaciones estándar mayor que la media.
¿Recibí esto? : Puntuaciones Z

