Muestreo

CO-2: Diferenciar entre diferentes métodos de muestreo y discutir sus fortalezas y limitaciones.

Video

Video: Muestreo (12:38)

Planes de Muestreo

Como se mencionó en la introducción a esta unidad, comenzaremos con la primera etapa de producción de datos: el muestreo. Nuestra discusión se enmarcará en torno a los siguientes ejemplos:

Supongamos que desea determinar las preferencias musicales de todos los estudiantes de su universidad, a partir de una muestra de estudiantes. Estos son algunos ejemplos de las muchas formas posibles de perseguir este problema.

Ejemplos: Muestreo

Ejemplo 1: Publicar una encuesta de amantes de la música en un tablón de anuncios de Internet universitario, pidiendo a los estudiantes que voten por su tipo de música favorita.

Este es un ejemplo de una muestra voluntaria, donde los individuos se han seleccionado a sí mismos para ser incluidos. Tal muestra está casi garantizada para ser sesgada. En general, las muestras voluntarias tienden a estar compuestas por individuos que tienen una opinión particularmente fuerte sobre un tema, y buscan una oportunidad para expresarlo. No se puede determinar si los valores de la variable obtenidos de dicha muestra están sobreestimados o subestimados, y en qué medida. En consecuencia, los datos obtenidos de una muestra de respuesta voluntaria son bastante inútiles cuando se piensa en el “Big Picture”, ya que los individuos muestreados solo proporcionan información sobre sí mismos, y no podemos generalizar a ningún grupo más grande en absoluto.

Comentario:

• Cabe mencionar que en algunos casos las muestras voluntarias son la única forma ética de obtener una muestra. En los estudios médicos, por ejemplo, en los que se prueban nuevos tratamientos, los sujetos deben optar por participar firmando un formulario de consentimiento que destaque los riesgos y beneficios potenciales. Como discutiremos en el siguiente tema sobre diseño de estudios, una muestra voluntaria no es tan problemática en un estudio realizado con el propósito de comparar varios tratamientos.

---

Ejemplo 2: Párese fuera de la Unión de Estudiantes, frente al Edificio de Bellas Artes, y pídale a los alumnos que pasan por ahí que respondan a su pregunta sobre la preferencia musical.

Este es un ejemplo de una muestra de conveniencia, donde los individuos pasan a estar en el momento y lugar adecuados para adecuarse al horario del investigador. Dependiendo de qué variable se esté estudiando, puede ser que una muestra de conveniencia proporcione un grupo bastante representativo. Sin embargo, a menudo hay razones sutiles por las que los resultados de la muestra están sesgados. En este caso, la proximidad al Edificio de Bellas Artes podría resultar en que un número desproporcionado de estudiantes favoreciera la música clásica. Una muestra de conveniencia también puede ser susceptible al sesgo porque ciertos tipos de individuos tienen más probabilidades de ser seleccionados que otros. En el extremo, algunas muestras de conveniencia están diseñadas de tal manera que ciertos individuos no tienen ninguna posibilidad de ser seleccionados, como en el siguiente ejemplo.

---

Ejemplo 3: Pide a tus profesores los rosters por correo electrónico de todos los alumnos de tus clases. Muestrea aleatoriamente algunas direcciones y envíanos un correo electrónico a esos estudiantes con tu pregunta sobre preferencia musical.

Aquí hay un caso en el que el marco de muestreo —lista de individuos potenciales para ser muestreados— no coincide con la población de interés. La población de interés está formada por todos los estudiantes de la universidad, mientras que el marco de muestreo consiste únicamente en tus compañeros de clase. Puede haber sesgo que surja debido a esta discrepancia. Por ejemplo, los estudiantes con especializaciones similares tenderán a tomar las mismas clases que tú, y sus preferencias musicales también pueden ser algo diferentes a las de la población general de estudiantes. Siempre es mejor que el marco de muestreo coincida con la población lo más cerca posible.

---

Ejemplo 4: Obtener un directorio de estudiantes con las direcciones de correo electrónico de todos los estudiantes de la universidad, y enviar la encuesta de música a cada 50 nombre de la lista.

Esto se denomina muestreo sistemático. Puede que no esté sujeto a ningún sesgo claro, pero no sería tan seguro como tomar una muestra aleatoria.

Si los individuos son muestreados completamente al azar, y sin reemplazo, entonces cada grupo de un tamaño dado es tan probable que sea seleccionado como todos los demás grupos de ese tamaño. Esto se llama una muestra aleatoria simple (SRS). En contraste, una muestra sistemática no permitiría seleccionar a los estudiantes hermanos, por tener el mismo apellido. En una simple muestra aleatoria, los estudiantes hermanos tendrían tantas posibilidades de que ambos sean seleccionados como cualquier otro par de estudiantes. Por lo tanto, puede haber fuentes sutiles de sesgo en el uso de un plan de muestreo sistemático.

---

Ejemplo 5: Obtener un directorio de estudiantes con las direcciones de correo electrónico de todos los estudiantes de la universidad, y enviar su encuesta de música a una simple muestra aleatoria de estudiantes.

Mientras todos los alumnos respondan, entonces la muestra no está sujeta a ningún sesgo, y debe tener éxito en ser representativa de la población de interés.

Pero, ¿y si solo el 40% de los seleccionados te envía un correo electrónico de vuelta con su voto?

Los resultados de esta encuesta no serían necesariamente representativos de la población, debido a los problemas potenciales asociados a la respuesta voluntaria. Dado que los individuos no están obligados a responder, a menudo un subconjunto relativamente pequeño se toma la molestia de participar. La respuesta voluntaria no es tan problemática como una muestra voluntaria (presentada en el ejemplo 1 anterior), pero aún existe el peligro de que quienes sí responden sean diferentes a los que no, con respecto a la variable de interés. Una mejora sería dar seguimiento con un segundo correo electrónico, pidiendo cortésmente la cooperación de los estudiantes. Esto puede impulsar la tasa de respuesta, resultando en una muestra que es bastante representativa de toda la población de interés, y puede ser lo mejor que puedas hacer, dadas las circunstancias. La falta de respuesta sigue siendo un problema, pero al menos has logrado reducir su impacto en tus resultados.

Hasta ahora hemos discutido varios planes de muestreo, y determinado que una simple muestra aleatoria es la única que discutimos que no está sujeta a ningún sesgo.

Una muestra aleatoria simple es la forma más fácil de basar una selección en la aleatoriedad. Hay otras técnicas de muestreo más sofisticadas que utilizan aleatoriedad que a menudo son preferibles en circunstancias de la vida real. Cualquier plan que se base en la selección aleatoria se denomina plan (o técnica) de muestreo probabilístico. Los siguientes tres planes de muestreo probabilístico se encuentran entre los más utilizados:

• El muestreo aleatorio simple es, como su nombre indica, el plan de muestreo probabilístico más simple. Es equivalente a “seleccionar nombres de un sombrero”. Cada individuo tiene las mismas posibilidades de ser seleccionado.

• Muestreo por conglomerados — Esta técnica de muestreo se utiliza cuando nuestra población se divide de forma natural en grupos (a los que llamamos clusters). Por ejemplo, todos los estudiantes de una universidad se dividen en especializaciones; todas las enfermeras de una ciudad determinada se dividen en hospitales; todos los votantes registrados se dividen en recintos (distritos electorales). En el muestreo por conglomerados, tomamos una muestra aleatoria de conglomerados, y utilizamos todos los individuos dentro de los conglomerados seleccionados como nuestra muestra. Por ejemplo, para obtener una muestra de estudiantes de último año de secundaria de una ciudad determinada, eliges 3 escuelas secundarias al azar de entre todas las escuelas secundarias de esa ciudad, y usas como muestra a todos los estudiantes de último año de secundaria en las tres escuelas secundarias seleccionadas.

• Muestreo estratificado — El muestreo estratificado se utiliza cuando nuestra población se divide naturalmente en subpoblaciones, a las que llamamos estrato (plural: estratos). Por ejemplo, todos los alumnos de una determinada universidad se dividen por género o por año en la universidad; todos los votantes registrados en una ciudad determinada se dividen por raza. En el muestreo estratificado, elegimos una muestra aleatoria simple de cada estrato, y nuestra muestra consiste en todas estas muestras aleatorias simples reunidas. Por ejemplo, para obtener una muestra aleatoria de estudiantes de último año de secundaria de una ciudad determinada, elegimos una muestra aleatoria de 25 adultos mayores de cada una de las escuelas secundarias de esa ciudad. Nuestra muestra consiste en todas estas muestras juntas.

Cada uno de esos planes de muestreo probabilístico, si se aplican correctamente, no están sujetos a ningún sesgo, y así producen muestras que representan bien a la población de la que fueron extraídos.

Comentario: Cluster vs. Estratified

• Los estudiantes a veces se confunden sobre la diferencia entre el muestreo por conglomerados y el muestreo estratificado. A pesar de que ambos métodos comienzan con la población de alguna manera dividida en grupos, los dos métodos son muy diferentes.
  • En el muestreo por conglomerados, tomamos una muestra aleatoria de grupos enteros de individuos tomando a todos en ese grupo pero no se toman todos los grupos), mientras que en el muestreo estratificado tomamos una muestra aleatoria simple de cada grupo (y todos los grupos están representados).
  • Por ejemplo, digamos que queremos realizar un estudio sobre los hábitos de sueño de los estudiantes de pregrado en una determinada universidad, y necesitamos obtener una muestra. Los estudiantes están naturalmente divididos por especializaciones, y digamos que en esta universidad hay 40 especializaciones diferentes.
    • En el muestreo por conglomerados, elegiríamos aleatoriamente, por ejemplo, 5 especializaciones (grupos) de las 40, y usaríamos a todos los estudiantes de estas cinco carreras como nuestra muestra.
    • En el muestreo estratificado, obtendríamos una muestra aleatoria de, digamos, 10 estudiantes de cada una de las 40 carreras (grupos), y utilizaríamos a los 400 estudiantes elegidos como muestra.
    • Claramente en este ejemplo, el muestreo estratificado es mucho mejor, ya que la mayor del estudiante podría tener un efecto en los hábitos de sueño del estudiante, por lo que nos gustaría asegurarnos de que contamos con representantes de todas las diferentes carreras. Volveremos a hacer hincapié en este punto siguiendo el ejemplo y la actividad.

EJEMPLO:

Supongamos que te gustaría estudiar la satisfacción laboral de los enfermeros hospitalarios en una ciudad determinada a partir de una muestra. Además de tomar una muestra aleatoria simple, aquí hay dos formas adicionales de obtener dicha muestra.

1. Supongamos que la ciudad cuenta con 10 hospitales. Elija uno de los 10 hospitales al azar y entrevistar a todas las enfermeras de ese hospital respecto a su satisfacción laboral. Este es un ejemplo de muestreo por conglomerados, en el que los hospitales son los clusters.

2. Elija una muestra aleatoria de 50 enfermeras de cada uno de los 10 hospitales y entreviste a estos 50 * 10 = 500 respecto a su satisfacción laboral. Este es un ejemplo de muestreo estratificado, en el que cada hospital es un estrato.

Cluster o Estratificado — ¿cuál es mejor?

Volvamos y volvamos a revisar el ejemplo de satisfacción laboral de las enfermeras hospitalarias y discutir los pros y los contras de los dos planes de muestreo que se presentan. Ciertamente, será mucho más fácil realizar el estudio utilizando la muestra de conglomerado, ya que todas las entrevistas se realizan en un solo hospital a diferencia de la muestra estratificada, en la que las entrevistas deben realizarse en 10 hospitales diferentes. Sin embargo, el hospital en el que trabaja una enfermera probablemente tenga un impacto directo en su satisfacción laboral, y en ese sentido, obtener datos de un solo hospital podría proporcionar resultados sesgados. En este caso, será muy importante contar con representación de todos los hospitales de la ciudad, por lo que la muestra estratificada es definitivamente preferible. Por otro lado, decir que en lugar de la satisfacción laboral, nuestro estudio se centra en la edad o el peso de las enfermeras hospitalarias.

En este caso, probablemente no sea tan crucial obtener representación de los diferentes hospitales, por lo que podría ser preferible la muestra de conglomerados más fácilmente obtenida.

Comentario:

• Otra técnica de muestreo comúnmente utilizada es el muestreo multietapa, que es esencialmente una “forma compleja” de muestreo por conglomerados. Al realizar el muestreo de conglomerados, puede ser poco realista o demasiado costoso muestrear todos los individuos en los conglomerados elegidos. En casos como este, tendría sentido tener otra etapa de muestreo, en la que elija una muestra de cada uno de los clústeres seleccionados aleatoriamente, de ahí el término muestreo multietapa.

Por ejemplo, digamos que te gustaría estudiar los hábitos de ejercicio de los estudiantes universitarios del estado de California. Podrías elegir 8 colegios (clusters) al azar, pero ciertamente no vas a usar a todos los estudiantes de estas 8 universidades como tu muestra. Simplemente no es realista realizar tu estudio de esa manera. En su lugar, pasas a la etapa 2 de tu plan de muestreo, en la que eliges una muestra aleatoria de 100 machos y una muestra aleatoria de 100 hembras de cada una de las 8 universidades que seleccionaste en la etapa 1.

Entonces en total tienes 8 * (100+100) = 1,600 estudiantes universitarios en tu muestra.

En este caso, la etapa 1 fue una muestra agrupada de 8 colegios y la etapa 2 fue una muestra estratificada dentro de cada colegio donde el estrato era de género.

El muestreo multietapa puede tener más de 2 etapas. Por ejemplo, para obtener una muestra aleatoria de médicos en Estados Unidos, eliges 10 estados al azar (etapa 1, cluster). De cada estado eliges al azar 8 hospitales (etapa 2, cluster). Por último, de cada hospital, eliges a 5 médicos de cada subespecialidad (etapa 3, estratificada).

¿Conseguí esto? : Muestreo

Descripción general Hasta ahora

Hemos definido lo siguiente:

Marco de Muestreo: Listado de individuos potenciales a ser muestreados. Queremos que el marco de muestreo coincida con la población lo más cerca posible. El marco de muestreo está incrustado dentro de la población y la muestra está incrustada dentro del marco de muestreo.

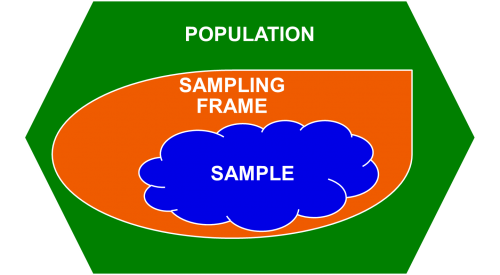
Muestra sesgada: Muestra que produce datos que no son representativos debido a la subestimación sistemática o sobreestimación de los valores de la variable de interés.

Muestra Voluntaria: Los individuos se han seleccionado a sí mismos para ser incluidos.

Muestra de Conveniencia: Los individuos se encuentran en el momento y lugar adecuados para adaptarse al horario del investigador

Muestra sistemática: A partir de un individuo elegido aleatoriamente en el marco de muestreo ordenado, seleccione cada individuo i-ésimo para ser incluido en la muestra.

Muestra Aleatoria Simple (SRS): Los individuos son muestreados completamente al azar, y sin reemplazo. El resultado es que CADA grupo de un tamaño dado tiene la misma probabilidad de ser seleccionado como todos los demás grupos de ese tamaño. También es igualmente probable que cada individuo sea elegido.

Muestreo por conglomerados: Se utiliza cuando las agrupaciones “naturales” son evidentes en una población estadística y cada grupo es generalmente representativo de la población. En esta técnica, la población total se divide en estos grupos (o conglomerados) y se selecciona una muestra de estos grupos. Por ejemplo, seleccionar aleatoriamente cursos de todos los cursos y encuestar a TODOS los estudiantes en cursos seleccionados.

Muestreo estratificado: Cuando las subpoblaciones dentro de una población general varían, puede ser ventajoso tomar muestras de cada subpoblación (estrato) de forma independiente. Por ejemplo, tomar una muestra aleatoria de machos y una muestra aleatoria separada de hembras.

No respuesta: Las personas seleccionadas para participar no responden o se niegan a participar.

Tamaño de la muestra

Hasta el momento, no hemos mencionado el tamaño de la muestra. Nuestra primera prioridad es asegurarnos de que la muestra sea representativa de la población, utilizando algún tipo de plan de muestreo probabilístico. A continuación, debemos tener en cuenta que para tener una idea más precisa de qué valores toma la variable de interés para toda la población, una muestra mayor hace un mejor trabajo que una menor. Discutiremos el tema del tamaño de la muestra con más detalle en la unidad de Inferencia, y de hecho veremos cómo los cambios en el tamaño de la muestra afectan las conclusiones que podemos sacar sobre la población.

EJEMPLO:

Supongamos que a los administradores del hospital les gustaría saber cómo calificaría el personal la calidad de los alimentos en la cafetería del hospital. ¿Cuál de los cuatro planes de muestreo a continuación sería mejor?

1. El responsable del sondeo se para afuera de la puerta de la cafetería y pide a los siguientes 5 miembros del personal que salgan que den una calificación a la comida en una escala del 1 al 10.

2. El responsable del sondeo se para afuera de la puerta de la cafetería y pide a los siguientes 50 miembros del personal que salgan que den una calificación a la comida en una escala del 1 al 10.

3. El responsable del sondeo toma una muestra aleatoria de 5 miembros del personal de la lista de todos los empleados en el hospital y les pide que califiquen la comida de la cafetería en una escala del 1 al 10.

4. El responsable del sondeo toma una muestra aleatoria de 50 miembros del personal de la lista de todos los empleados en el hospital y les pide que califiquen la comida de la cafetería en una escala del 1 al 10.

Los planes 1 y 2 estarían sesgados a favor de calificaciones más altas, ya que los miembros del personal con opiniones desfavorables sobre la comida de la cafetería probablemente comerían en otro lugar. El plan 3, al ser aleatorio, sería imparcial. Sin embargo, con una muestra tan pequeña, corres el riesgo de incluir a personas que proporcionan calificaciones inusualmente bajas o inusualmente altas. En otras palabras, la calificación promedio podría variar bastante dependiendo de quién pasa a estar incluido en esa pequeña muestra. El plan 4 sería lo mejor, ya que los participantes han sido elegidos al azar para evitar sesgos y el mayor tamaño muestral brinda más información sobre las opiniones de todos los miembros del personal del hospital.

EJEMPLO:

Supongamos que se requiere que un alumno inscrito en un curso de estadística complete y entregue varios cientos de problemas de tareas a lo largo del semestre. El asistente docente responsable de la calificación sugiere al profesor del curso el siguiente plan: en lugar de calificar todos los problemas para cada alumno, calificará una muestra aleatoria de problemas.

Su primera oferta, de calificar una muestra aleatoria de tan solo 3 problemas por cada alumno, no es bien recibida por el profesor, quien teme que una muestra tan pequeña pueda no proporcionar una estimación muy precisa del desempeño general de la tarea de un estudiante.

Los estudiantes están particularmente preocupados de que la selección aleatoria pueda pasar a incluir uno o dos problemas en los que se desempeñaron mal, con lo que bajaron su calificación.

La siguiente oferta, para calificar una muestra aleatoria de 25 problemas por cada alumno, es considerada aceptable tanto por el profesor como por los alumnos.

Comentario:

• En la práctica, nos enfrentamos a muchas compensaciones en la estadística. Una muestra más grande es más informativa sobre la población, pero también es más costosa en términos de tiempo y dinero. Los investigadores deben hacer un esfuerzo para mantener bajos sus costos, pero aún así obtener una muestra que sea lo suficientemente grande como para permitirles reportar resultados bastante precisos.

Aprender haciendo: Muestreo (Software)

Resumimos

Nuestro objetivo, en estadística, es utilizar la información de una muestra para sacar conclusiones sobre el grupo más grande, llamado población. El primer paso en este proceso es obtener una muestra de individuos que sean verdaderamente representativos de la población. Si este paso no se lleva a cabo adecuadamente, entonces la muestra está sujeta a sesgos, una tendencia sistemática a tergiversar las variables de interés en la población.

El sesgo está casi garantizado si se utiliza una muestra voluntaria. Si los individuos se seleccionan a sí mismos para el estudio, a menudo son diferentes de manera importante de los individuos que no se ofrecieron como voluntarios.

Una muestra de conveniencia, elegida porque los individuos estaban en el lugar adecuado en el momento adecuado para adaptarse al investigador, puede ser diferente de la población general de una manera sutil pero importante. Sin embargo, para ciertas variables de interés, una muestra de conveniencia aún puede ser bastante representativa.

El marco de muestreo de los individuos de los que realmente se selecciona la muestra debe coincidir con la población de interés; puede resultar sesgo si partes de la población son sistemáticamente excluidas.

El muestreo sistemático toma un enfoque organizado (pero no aleatorio) del proceso de selección, como al elegir cada nombre número 50 en una lista, o el primer producto que sale de la línea de producción cada hora. Al igual que con el muestreo de conveniencia, puede haber fuentes sutiles de sesgo en dicho plan, o puede ser adecuado para el propósito en cuestión.

La mayoría de los estudios están sujetos a algún grado de falta de respuesta, refiriéndose a individuos que no están de acuerdo con la intención de los investigadores de incluirlos en un estudio. Si hay demasiados no encuestados, y son diferentes de los encuestados de manera importante, entonces la muestra resulta estar sesgada.

En general, el sesgo puede eliminarse (en teoría), o al menos reducirse (en la práctica), si los investigadores hacen todo lo posible para implementar un plan de muestreo probabilístico que utilice aleatoriedad.

El plan de muestreo probabilístico más básico es una muestra aleatoria simple, donde cada grupo de individuos tiene las mismas posibilidades de ser seleccionados que cualquier otro grupo del mismo tamaño. Esto se logra mediante muestreo al azar y sin reemplazo.

En una muestra de conglomerado, se seleccionan aleatoriamente grupos de individuos, como todas las personas del mismo hogar. En una muestra de conglomerado, todos los miembros de cada grupo seleccionado participan en el estudio.

Una muestra estratificada divide a la población en grupos llamados estratos antes de seleccionar a los participantes del estudio al azar dentro de esos grupos.

El muestreo multietapa hace que el proceso de muestreo sea más manejable al trabajar desde una población grande hasta grupos sucesivamente más pequeños dentro de la población, aprovechando la estratificación en el camino y, en ocasiones, terminando con una muestra de racimo o una muestra aleatoria simple.

Suponiendo que se han evitado las diversas fuentes de sesgo, los investigadores pueden aprender más sobre las variables de interés para la población tomando muestras más grandes. El “extremo” (es decir, la muestra más grande posible) sería estudiar a cada individuo de la población (objetivo de un censo), pero en la práctica, tal diseño rara vez es factible. En cambio, los investigadores deben tratar de obtener la muestra más grande que se ajuste a su presupuesto (tanto en términos de tiempo como de dinero), y deben tener mucho cuidado de que la muestra sea verdaderamente representativa de la población de interés.

Discutiremos el tema del tamaño de la muestra cuando abarquemos distribuciones de muestreo y estadísticas inferenciales.

En esta breve sección sobre muestreo, aprendimos diversas técnicas mediante las cuales se puede elegir una muestra de individuos de toda una población para recolectar datos. Esto parece ser un paso simple en el panorama general de la estadística, pero resulta que tiene un efecto crucial en las conclusiones que podemos extraer de la muestra sobre toda la población (es decir, inferencia).

Precaución

En términos generales, un plan de muestreo probabilístico (como una muestra aleatoria simple, agrupamiento o muestreo estratificado) dará como resultado una muestra no sesgada, que se puede usar de manera segura para hacer inferencias. Además, los procedimientos inferenciales que aprenderemos más adelante en este curso suponen que la muestra fue elegida al azar.

Dicho esto, hay disponibles otras técnicas de muestreo (no aleatorias), y en ocasiones utilizarlas es lo mejor que podemos hacer. Sin embargo, es importante, cuando se utilizan estas técnicas, conocer los tipos de sesgo que introducen, y así las limitaciones de las conclusiones que pueden extraerse de las muestras resultantes.