2.5.6: Usar Ogives para encontrar percentiles
- Page ID
- 151694
La tabla de frecuencias relativas acumuladas se puede utilizar para encontrar percentiles para los puntos finales. Un método para estimar otros percentiles de los datos es mediante la creación de un gráfico especial de frecuencias relativas acumulativas, llamado Ogive.
Un Ogive es un gráfico de líneas donde el eje vertical es la frecuencia relativa acumulativa y el eje horizontal es el valor de los datos, específicamente los puntos finales de los intervalos de clase. El punto final izquierdo del intervalo de primera clase tendrá una frecuencia relativa acumulativa de cero. Todos los demás puntos finales reciben el punto final correcto del intervalo de clase correspondiente. Los puntos se conectan entonces por segmentos de línea.
Luego se puede leer la gráfica para encontrar cualquier percentil deseado. Por ejemplo, los percentiles 25 º, 50 º y 75 º rompen los datos en cuartos iguales y se denominan cuartiles.
Definición: Percentil
Percentil ‐ el valor de los datos por debajo del cual cae un porcentaje dado de los datos.
El percentil 25 también se conoce como el primer cuartil.
El percentil 50 también se conoce como el segundo cuartil o mediana.
El percentil 75 también se conoce como el cuartil 3.
Ejemplo: Estudiantes navegando por la web
Podemos referirnos al gráfico de frecuencia relativa acumulativa que se muestra en el ejemplo anterior para hacer el Ogive que se muestra aquí.
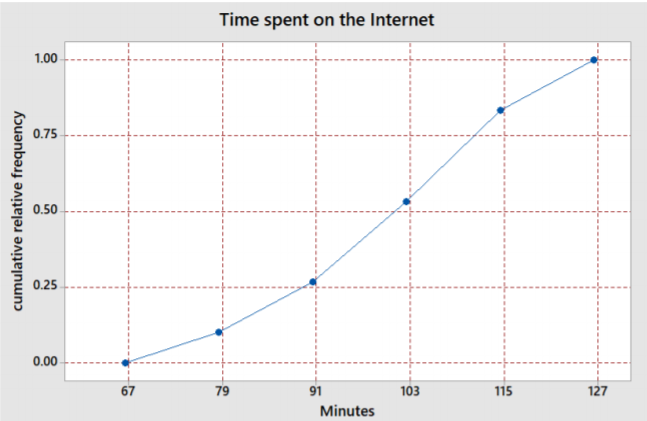
Usando la gráfica, podemos estimar los cuartiles de las distribuciones por donde el gráfico de líneas cruza valores de frecuencia relativa acumulados de 0.25, 0.50 y 0.75.
El 1er Cuartil es de unos 87 minutos.
La mediana es de unos 100 minutos.
El 3er Cuartil es de unos 108 minutos.
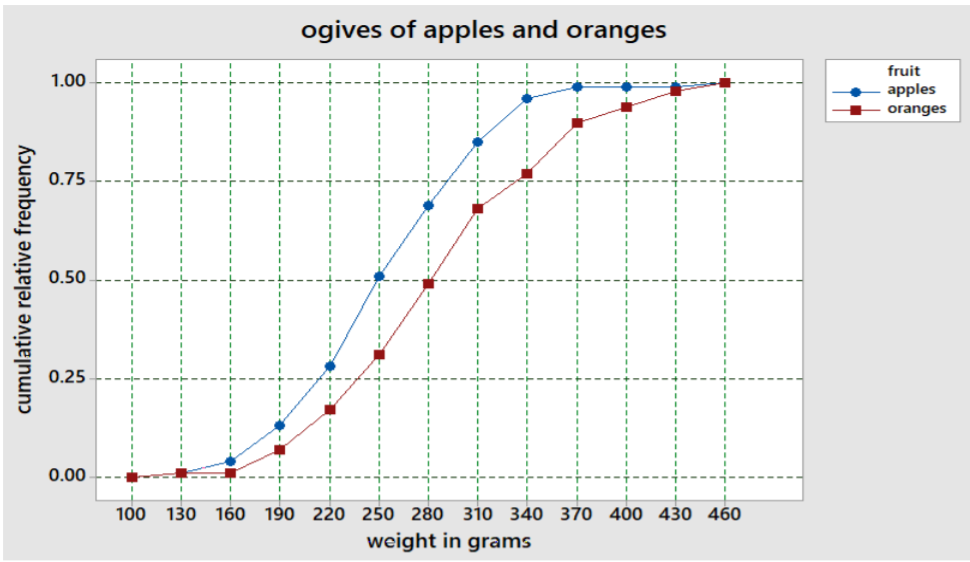
Ejemplo: Comparando pesos de manzanas y naranjas
Para las frecuencias relativas acumuladas de los pesos de manzanas y naranjas, podemos poner ambos ojivas en una sola gráfica y estimar los cuartiles.

Gráficas de líneas con tiempo
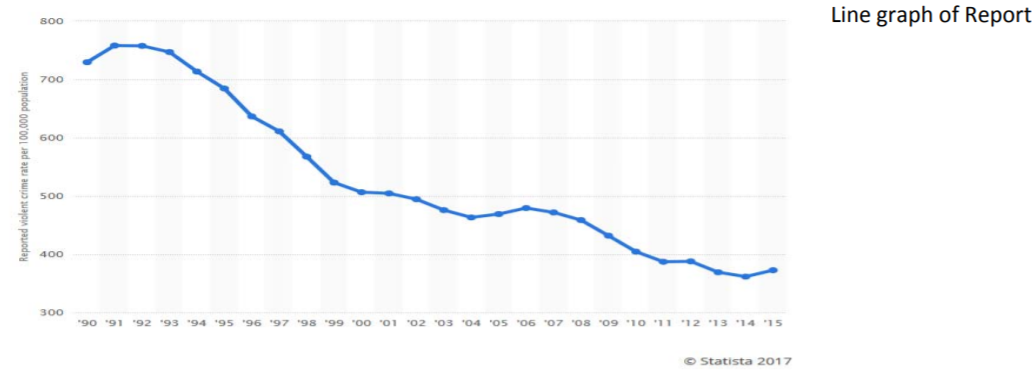
El ogive es un ejemplo de un gráfico de líneas. Un gráfico de líneas muy útil es aquel en el que el tiempo es el eje horizontal. Un ejemplo temprano de la Sección 1.1 de este tipo de gráficas lineales son los índices históricos de delincuencia. El gráfico de líneas muestra que el crimen violento ha disminuido con el tiempo.
Ejemplo: Grandes huracanes en el Océano Atlántico
En un periodo de un mes en 2017, cuatro huracanes mayores (categoría 3 o superior) se formaron en el Océano Atlántico. Tres de estos huracanes causaron daños devastadores y costosos a regiones de Estados Unidos: el huracán Harvey en Texas, el huracán Irma en Florida y el huracán María en Puerto Rico y las Islas Vírgenes. También hubo daños catastróficos por estas tormentas en Cuba, Dominica y otros países, islas y territorios del Caribe.
Un gráfico de Google Analytic muestra que se prestó mucha más atención al huracán Irma a lo largo de los días que amenazaba a Florida. 22
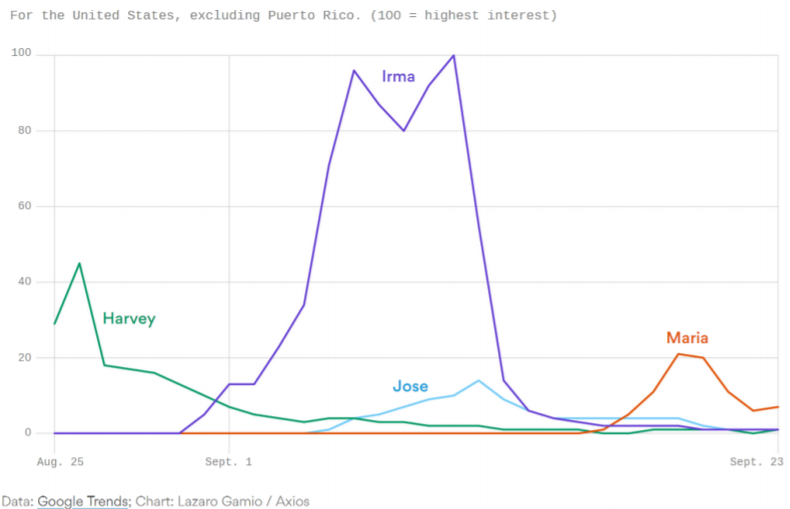
Sin embargo, Google Analytics excluye a Puerto Rico que recibió un golpe directo del huracán María. También podría ser que después de que Harvey causó inundaciones masivas en Houston y cerca de Houston, más personas se interesaron por toda la actividad de huracanes.


