7.1: ¿Qué es una Variable Aleatoria Continua?
- Page ID
- 151720
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Una variable aleatoria continua es una variable aleatoria que solo tiene valores continuos. Los valores continuos son incontables y están relacionados con números reales.
Ejemplos de variables aleatorias continuas
- El tiempo que lleva completar un examen para una prueba de 60 minutos Valores posibles = todos los números reales en el intervalo [0,60]
- Edad de un fósil Valores posibles = todos los números reales en el intervalo [edad mínima, edad máxima]
- Millas por galón para un Toyota Prius Valores Posibles = todos los números reales del intervalo [MPG mínimo, MPG máximo]
La principal diferencia entre las variables aleatorias continuas y discretas es que la probabilidad continua se mide a lo largo de intervalos, mientras que la probabilidad discreta se calcula en puntos exactos.
Por ejemplo, no tendría sentido encontrar la probabilidad de que tardó exactamente 32 minutos en terminar un examen. Podría tomarte 32.012342472... minutos. La probabilidad de puntos ya no tiene sentido cuando pasamos de variables aleatorias discretas a continuas.
En cambio, podrías encontrar la probabilidad de tomar al menos 32 minutos para el examen, o la probabilidad de tomar entre 31 y 33 minutos para completar el examen. En lugar de asignar probabilidad a puntos, definimos una función de densidad de probabilidad (pdf) que nos ayudará a encontrar probabilidades. Esta función siempre debe tener un rango no negativo (salida). La probabilidad puede entonces ser determinada encontrando el área bajo la función. Para ser una función de densidad de probabilidad válida, el área total bajo la curva debe ser igual a 1.
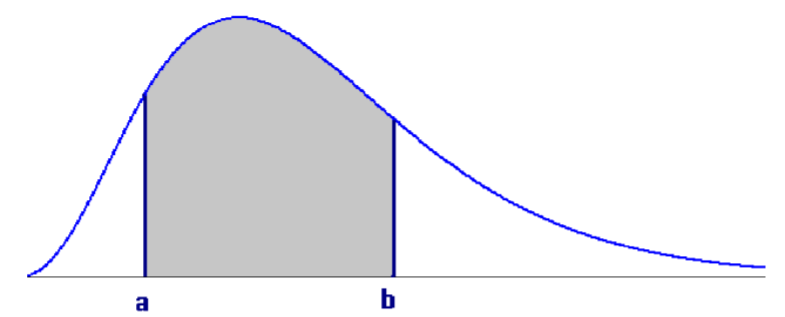
Si el dibujo representa una función de densidad de probabilidad válida para una variable aleatoria\(X\), entonces
\[P(a<X<b)=\text { shaded area } \nonumber \]
Esta tabla muestra las similitudes y diferencias entre distribuciones discretas y continuas
| Distribuciones Discretas | Distribuciones continuas |
|---|---|
|
Contable Puntos Discretos Los puntos tienen probabilidad \(p(x)\)es la función de distribución de probabilidad \(p(x) \geq 0\) \(\Sigma p(x)=1\) |
Incontable Intervalos Continuos Los puntos no tienen probabilidad \(f(x)\)es la función de densidad de probabilidad \(f(x) \geq 0\) Área total bajo curva =1 |
Ejemplo: Conducir a la escuela
El tiempo de conducir a la escuela para un estudiante de un colegio comunitario es un ejemplo de una variable aleatoria continua. La función de densidad de probabilidad y las áreas de regiones creadas por los puntos 15 y 25 minutos se muestran en la gráfica.
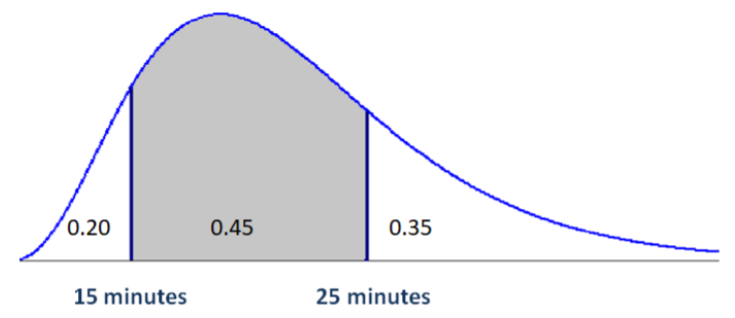
- Encuentra la probabilidad de que un estudiante tarda menos de 15 minutos en conducir a la escuela.
- Encuentra la probabilidad de que un estudiante no tome más de 15 minutos en conducir a la escuela. Esta respuesta es la misma que la pregunta anterior, porque los puntos no tienen probabilidad con variables aleatorias continuas.
- Encuentra la probabilidad de que un estudiante tome más de 15 minutos en conducir a la escuela.
- Encuentra la probabilidad de que un estudiante tome entre 15 y 25 minutos en conducir a la escuela.
Solución
- \(P(X<15)=0.20\)
- \(P(X \leq 15)=0.20\)
- \(P(X>15)=0.45+0.35=0.80\)
- \(P(15 \leq X \leq 25)=0.45\)
También podemos utilizar un modelo de distribución continua para determinar percentiles.
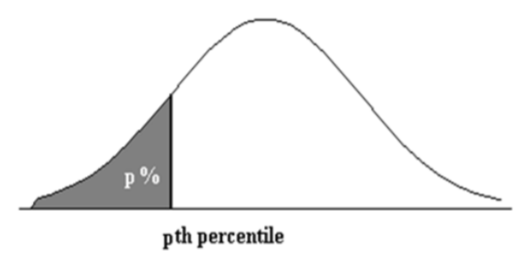
El\(p^{th}\) percentil es el valor\(x_p\) tal que\(P\left(X<x_{p}\right)=p\)
Encuentra los\(65^{th}\) percentiles\(20^{th}\) y de los tiempos conduciendo a la escuela.
A partir del dibujo\(X_{20} = 15\) minutos y\(X_{65} = 25\) minutos
Valor esperado y varianza de variables aleatorias continuas
La media y varianza se pueden calcular para la mayoría de las variables aleatorias continuas. Los cálculos reales requieren cálculo y están más allá del alcance de este curso. Utilizaremos los mismos símbolos para definir el valor esperado y la varianza que se utilizaron para las variables aleatorias discretas.
Valor esperado (\(\mu\)) and Variance (\(\sigma^{2}\)) of Continuous Random Variable \(X\)
Valor esperado (media poblacional):\(\mu=E(x)\)
Varianza poblacional:\(\sigma^{2}=\operatorname{Var}(x)=E\left[(x-\mu)^{2}\right]\)
Desviación estándar poblacional:\(\sigma=\sqrt{\operatorname{Var}(x)}\)
Estas siguientes secciones exploran tres variables aleatorias continuas especiales que tienen aplicaciones prácticas.


