7.2: Distribución exponencial
- Page ID
- 151719
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)La distribución exponencial se utiliza a menudo para modelar el tiempo de espera hasta que ocurra un evento. Por ejemplo, el tiempo de espera hasta recibir un mensaje de texto o el tiempo de espera hasta un accidente en una planta de fabricación seguirá una distribución exponencial.
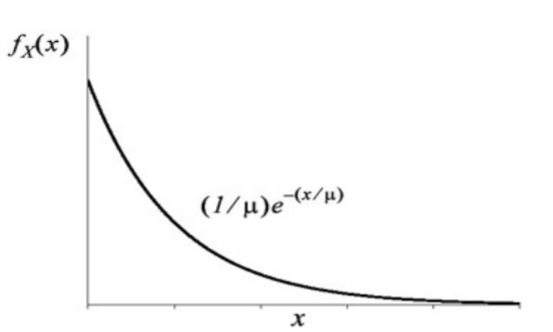
Este modelo tiene un parámetro, el tiempo de espera esperado,\(\mu\).
Una suposición importante para el Exponencial es que el tiempo de espera futuro esperado es independiente del tiempo de espera pasado. Por ejemplo, si esperas esperar 5 minutos para recibir un mensaje de texto y esperas 3 minutos, el tiempo de espera esperado en ese punto sigue siendo de 5 minutos.
Esto se puede escribir como una declaración de probabilidad:\(P(X>a)=P(X>a+b \mid X>b)\)
La Distribución Exponencial es útil para modelar el tiempo de espera hasta que algo se “rompa”, pero no sería el modelo apropiado para algo que “se desgasta”.
Distribución exponencial de probabilidad (parámetro=\(\mu\))
\(\mu\)= tiempo de espera esperado hasta que ocurra el evento.
\(X\)= tiempo de espera hasta que ocurra el evento
Asunción: El tiempo de espera en el futuro es independiente del tiempo de espera en el pasado:
\(P(X>a)=P(X>a+b \mid X>b)\)
\(\sigma^{2}=\mu^{2}\)
\(\sigma=\mu\)
Ejemplo: Pantalla agrietada en el teléfono inteligente.

El tiempo hasta que se agrieta una pantalla en un teléfono inteligente tiene una distribución exponencial con\(\mu=500\) horas de uso.
- Encuentra la probabilidad de que la pantalla no se agriete durante al menos 600 horas.
- ¿Cuál es la mediana del tiempo hasta que se agrieta la pantalla del teléfono inteligente?
Solución
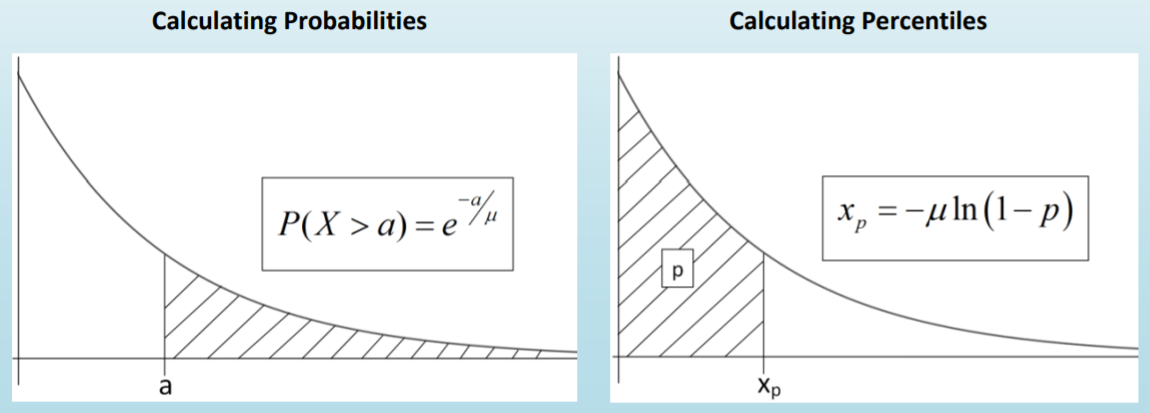
- Aquí usamos la fórmula para un problema de probabilidad,\(P(X>a)=e^{-a / \mu}\)
\[P(x>600)=e^{-600 / 500}=e^{-1.2}=.3012 \nonumber \]
Suponiendo que la pantalla ya haya durado 500 horas sin agrietarse, encuentre la posibilidad de que la pantalla dure 600 horas adicionales.
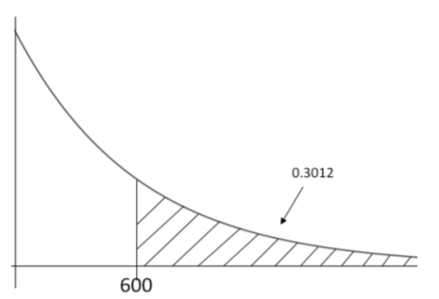
Debido a la característica sin memoria de la distribución exponencial, la respuesta será la misma que si nunca se usara el teléfono inteligente.
\[P(x>1100 \mid x>500)=P(x>600)=.3012 \nonumber \]
- Debido a que la distribución exponencial siempre está sesgada positivamente, la mediana será menor que la media de 500 horas. La mediana es el\(50^{th}\) percentil, por lo que este es un problema de percentil. Podemos derivar la fórmula para el\(p^{th}\) percentil (\(x_p\)) usando álgebra:
\ [\ begin {alineado}
P\ izquierda (x>x_ {p}\ derecha) =e^ {-x_ {p}/\ mu} &=1-p\\
-x_ {p}/\ mu&=\ ln (1-p)\\
x_ {p} &=-\ mu\ ln (1-p)
\ end {alineado}\ nonumber\]
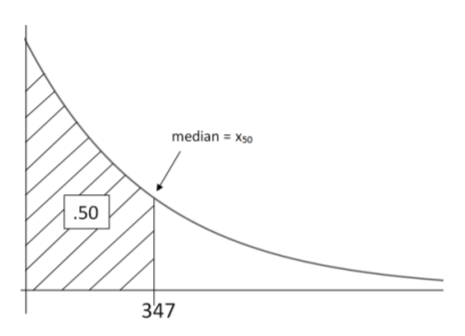
mediana de\(=x_{50}=-500 \ln (1-0.5)=347\) horas
Esto significa que la mitad de los teléfonos inteligentes tendrán pantallas agrietadas después de 347 horas de uso.
Relación entre la distribución exponencial y la distribución de Poisson
Existe una relación entre la Distribución de Poisson, (cubierta en el Capítulo 6 sobre distribuciones discretas) y la Distribución Exponencial. Recordemos que las distribuciones de Poisson modelan el número de ocurrencias en un periodo de tiempo fijo si la tasa que ocurren los eventos sigue una tasa constante. Una variable aleatoria que sigue a una distribución de Poisson se llama Proceso de Poisson.
Si las ocurrencias siguen un Proceso de Poisson con media =\(\mu\), entonces el tiempo de espera para la siguiente ocurrencia tiene una distribución exponencial con media =\(1 / \mu\).
Ejemplo: Accidentes en una refinería de petróleo 68
Los accidentes ocurren en una refinería de petróleo a una tasa constante de 3 por mes. Este es un ejemplo de un Proceso de Poisson.

La variable aleatoria\(Y\) = el número de accidentes en el próximo mes seguiría una Distribución de Poisson con\(\mu=3\) ocurrencias por mes
La Variable Aleatoria\(X\) = el tiempo de espera hasta el siguiente accidente de refinería seguiría una distribución exponencial con\(\mu=1 / 3\) meses.
- Encuentra la probabilidad de esperar menos de 2 meses para el próximo accidente de refinería de petróleo.
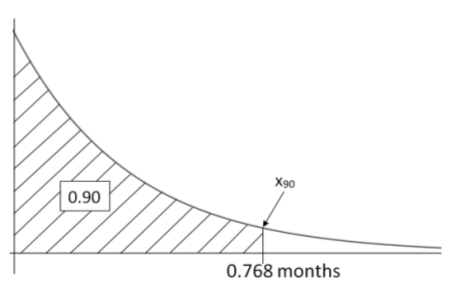
- Encuentra el\(90^{th}\) percentil de tiempos de espera para un accidente de refinería
Solución
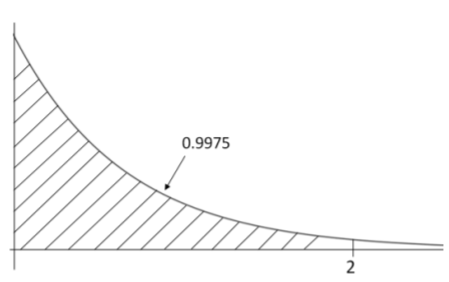
- \(P(X<2)=1-e^{-2 /(1 / 3)}=1-e^{-6}=0.9975\)
- \(x_{95}=-\dfrac{1}{3} \ln (1-.90)=0.768\)meses